非均匀划分拟阵约束下的多样性推荐方法*
2019-02-13和凤珍石进平
和凤珍,石进平
1.云南大学旅游文化学院 信息学院,云南 丽江 674100
2.云南省农村信用社 科技结算中心,昆明 650228
1 引言
作为一种从大量冗余信息中挖掘用户感兴趣的内容并推送给用户的有效手段,推荐系统(recommender system)已经成功应用到移动APP应用[1]、学术文献[2]、电子商务[3]、音乐[4]、电影[5-7]、Web社区发现[8]、信息检索[9-10]等广泛领域中。已有的推荐算法侧重提高推荐结果的相关性和准确度,如文献[4,6-7],但是缺乏多样性(diversity)。文献[11]研究表明:具有多样性的推荐结果有助于提高用户的整体满意度。由此可见,相关性不是衡量推荐质量的唯一标准,多样性对于提升推荐服务质量也具有重要作用。在实际推荐系统应用环境中,由于用户的偏好很难被准确描述和获取,往往具有不确定性、模糊性以及多义性。因此,如何基于已有的用户偏好信息,向用户推荐与其兴趣相关同时又具有非冗余、多样化的推荐结果,这成为当前推荐系统研究面临的主要挑战[12]。
针对多样性推荐问题,已有一些相关研究成果[4,10,13]。利用这些方法获得的推荐结果不能在多样性与相关性之间取得较好的折中。这是因为它们受到均匀拟阵约束(uniform matroid constraints),即假设推荐项目集中的各个推荐项对于所有用户具有相同的重要性,如文献[4,10]。文献[13]考虑到每个推荐项具有不同的重要性,但尚未考虑用户的偏好,会导致推荐结果中相同类别中的推荐项具有较高的冗余度。受此启发,本文提出了一种非均匀划分拟阵约束下的基于用户偏好的多样性推荐模型(preferencebased diversified recommendation model,PDM)。该模型在推荐过程中同时考虑了多样性和相关性两个因素,在保证推荐结果相关性的前提下,通过在每个类别上施加非均匀划分拟阵约束,有效提升推荐结果的多样性,力争在相关性和多样性之间取得有效折中。
图1展示了PDM的基本思想及与其他主流方法的不同。不同的字母代表不同类别,假设它们都与查询内容相关,但彼此之间具有差异性。假设大写字母和小写字母属于同一类别,但与查询内容的相关度不一样:大写字母的相关度大于小写字母。假设虚线框内的字母与查询内容的相关度大于其他类别。
在均匀拟阵约束(即基约束)下的推荐结果记作R,均匀拟阵假设各个推荐项对于所有用户具有相同的重要性,因此与用户兴趣相关度较高的推荐项被重复选择作为推荐结果,从而导致均匀拟阵约束下的推荐结果R仅来自少数几个与用户兴趣相关度较高的类别中,即C、B、O,而不能覆盖整个物品类别。非均匀拟阵约束下的Max-sum[13]方法,其认为每个推荐项的重要程度不同。然后,从与用户兴趣相关的每个类别中取相同数目的推荐项构成top-k推荐列表,使得Max-sum模型的效用函数最大化,如图1中R′所示,从每个相关的类别中取2个推荐项构成top-10推荐列表,因此,R′中的类别覆盖范围比R更广泛,多样性较好。在非均匀划分拟阵约束(即不仅考虑了每个推荐项具有不同的重要性,而且还考虑到不同用户对每个类别的偏好程度不同以及用户对相同类别中推荐项之间差异化的偏好程度也不同)下,选择使得PDM模型的效用函数最大化的推荐列表记作R*,如图1中R*所示,R*与R′都覆盖了所有的类别,根据前面的分析,在R中用户对类别C、B、O感兴趣的程度大于类别D、P,在覆盖广泛类别的同时也应当体现出用户的偏好,但是R′中每个类别中推荐项的数目均相同,而R*中不仅来自类别C、B、O、D、P的数目不完全相同,分别为3、2、2、2、1,而且R*中有来自同一类别C的“C,c,C”三个彼此差异化较大的推荐项,而R′中来自类别C的两个推荐项“C,C”彼此相同,没有差异化。R*比R′的差异化更大,多样性更丰富。这是由于在PDM模型中同时考虑了用户不同的偏好:用户不仅偏好能够覆盖广泛类别的推荐结果,而且也偏好相同类别中差异性较大的推荐结果。如图1左边的方框所示:均匀拟阵约束下所有推荐项属于同一类别且重要程度相同;非均匀拟阵约束下仅考虑到推荐项的重要程度,而未考虑类别之间的重要程度;而非均匀划分拟阵约束将推荐项划分为不同的类别(如图1中虚线框所示,未标出所有的虚线框),每个类别中推荐项的重要程度不同,而且不同类别的重要程度也不同。
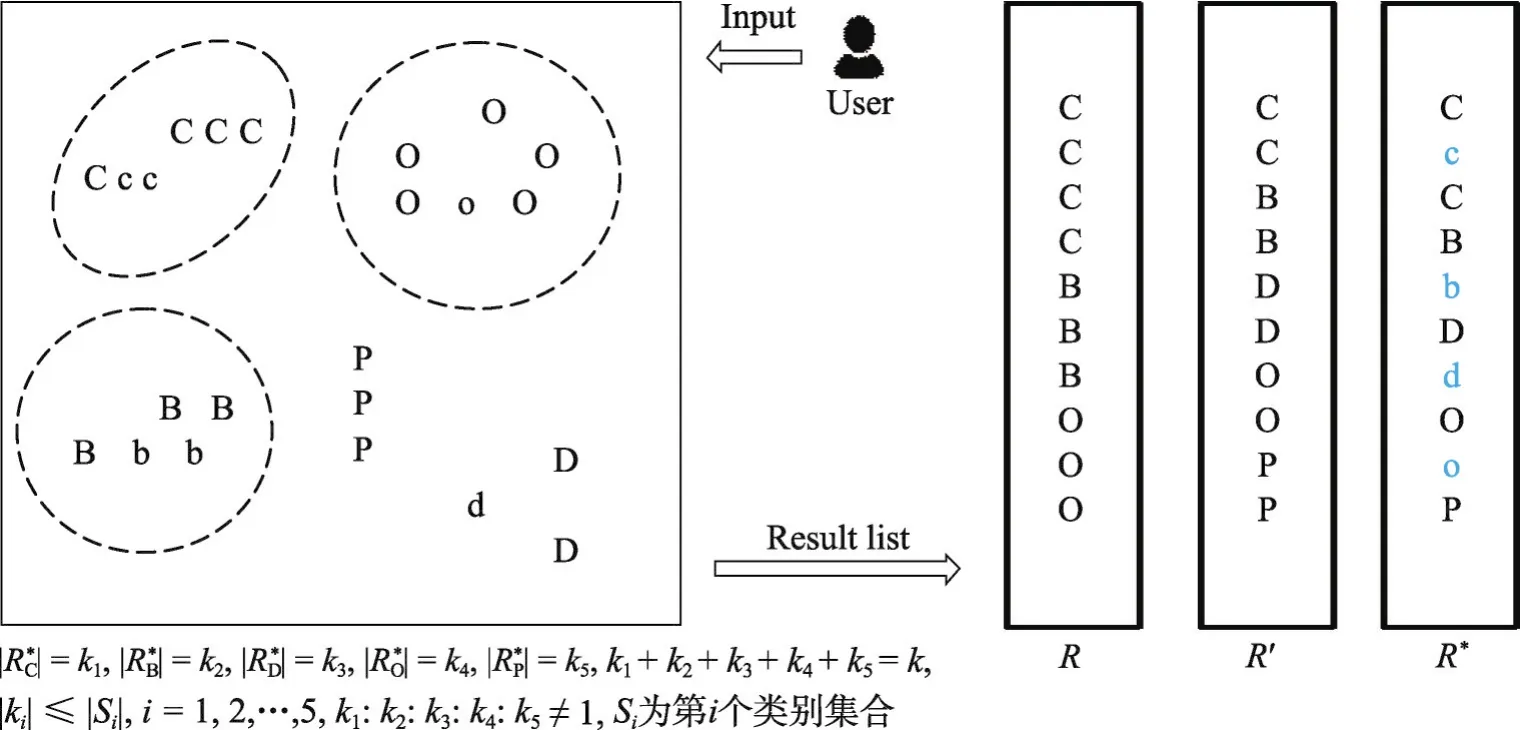
Fig.1 Basic idea of PDM and its differences from other mainstream methods图1 PDM的基本思想及与其他主流方法的不同
本文工作的主要贡献如下:
(1)为有效折中推荐结果的相关性和多样性,提出了一种非均匀划分拟阵约束条件下基于用户偏好的多样性推荐模型。该模型以一个具有子模性的目标函数来度量top-k推荐结果的推荐质量,在推荐过程同时融合了用户偏好的多样性和相关性。
(2)证明了使多样性效用函数最大化问题是一个NP-hard,并进一步提出一个高效率的近似优化算法——PDM多样性算法,进一步提出高效的贪心算法求解子模函数,能够获得(1-1/e)的近似保证。
(3)提出一种新颖的多样性度量方法DisCover-Div,此多样性度量方法融合了推荐列表的不相似度和类别覆盖程度,更加全面、多方位地度量推荐结果的多样性。
(4)在真实的数据集上进行实验,与多种算法在多样性和准确率(相关性)两方面进行分析比较,实验证明所提方法不仅能够在多样性和准确率之间取得较好的折中,而且具有高效性。
2 相关工作
目前,针对推荐系统中的多样性研究存在的问题,需要进行以下三方面研究[12]:(1)在多样性度量方式上,主要关注如何评价整体用户对多样性结果的满意度;(2)在相关性方面,主要研究如何在多样性和相关性之间找到一个良好的平衡点,而不是以牺牲准确度为代价换取多样性的提升;(3)在算法方面,主要研究推荐过程中高效率、新颖的多样性推荐算法。
近年来,许多研究者针对推荐系统中推荐结果多样性的度量方法、多样性最大化以及多样性推荐算法等问题积极开展研究,并取得了一系列成果,极大地促进了推荐系统多样化问题的研究[1-5,14-17]。然而,多样性与相关性之间是一种对立关系:随着多样性的提高,相关性将降低[14]。在不以牺牲相关性为代价的前提下,使得多样性最大化[13,18-21]等问题引起学者的关注,取得了一些初步的研究成果。
例如:文献[2]将多样性应用到学术领域,利用MutualRank对学术网络中的论文及作者的权威度进行建模,提出了一种面向权威度(相关性)和多样性的两阶段排序模型PDRank,给出一个融合相关性和多样性两个因素的线性目标函数。文献[3]展现了推荐列表多样性的重要性,提出了DivRec多样性推荐框架,通过设置相关性阈值调节推荐列表的多样性,该方法过滤了与用户相关度不高的物品,只考虑了用户感兴趣物品范围内的多样性。Lee等[4]介绍了基于图(graph)的个性化多样性推荐方法,提出了一种基于熵模型的GraphRec算法。Adomavicius等[15]基于商品流行程度提出一种整体多样性重排序方法,但是过于流行的商品会在许多用户的推荐结果中出现,从而降低了推荐结果的整体多样性。Bradley等[21]首先将多样性作为衡量指标引入到推荐系统中,并提出了整合多样性和准确度的线性模型,给出了一种求解该模型的贪心选择算法BGS(bounded greedy selection)。Hurley等[11]基于文献[21]进一步扩展,将多样性问题建模为一个动态规划问题,同样采用目标函数优化的方式获得与文献[21]相似的多样性,但时间复杂度更高。然而,这些多样性模型仅考虑使推荐列表中物品之间的相异性最大化,并没有考虑使推荐结果覆盖广泛的类别,因此推荐结果仅来自与用户兴趣爱好相关度较高的少数几个类别。
虽然一些文献考虑了类别多样性,例如,文献[1]提出了将用户的主题模型和移动应用APP的主题模型与协同过滤相结合的LDA_MF模型,并提出了结合主题模型LDA(latent Dirichlet allocation)和矩阵分解MF(matrix factorization)的LDA_MF算法,最后为了整合其他算法的优点,提出了通过逻辑回归将LDA_MF算法与其他协同过滤算法相融合的混合算法Hybrid_Rec,提高推荐结果的多样性。Aytekin等[5]提出一种基于聚类的多样性推荐模型ClusDiv。文献[8]基于网络设计中用户之间的关系网络和社区主题,提出一种新颖性社区推荐方法NovelRec,这种新颖性推荐本质上也是一种多样性,旨在向用户推荐其潜在感兴趣但又尚未触及的新社区。该方法虽然能够获得相对较好的新颖性推荐结果,但同时也牺牲了推荐结果的准确度。Ziegler等[14]首先提出话题多样性(topic diversification),并给出了在ILS模型下,使得推荐结果能够覆盖更多话题类别的重排序方法。但是,文献[1,5,8,14]依旧假设项目集合中所有项目的重要程度都是相同的,即受到均匀拟阵约束,因此,这些方法不能够在多样性和相关性之间取得较好的折中。
实际上,每个推荐项的重要程度是不相同的,不同用户对推荐项类别的偏好程度以及相同类别下推荐项之间的偏好程度也不一样,而且这些情况往往是同时存在的,针对这种情况下的多样性研究较少。Wu等[13]考虑了每张图像具有不同的重要性,通过引入困难系数自动调节每张图像的不同权重,提出了Max-sum模型,证明了Max-sum目标函数满足子模性,并在非均匀拟阵约束下提出一种高效率的近似优化算法,避免更多的图像来自相同类别。虽然Max-sum模型能够覆盖广泛的类别,但是Maxsum模型在每个类别划分上均取相同数目的图像构成top-k推荐列表,即Max-sum模型没有考虑不同用户对图像类别的偏好程度;其次,Max-sum模型没有考虑相同类别内图像之间的差异化,即Max-sum模型会导致推荐结果中相同类别下图像的冗余度较高。因此,Max-sum模型降低了推荐结果的多样性。
3 基于非均匀划分拟阵约束的多样性模型
3.1 问题定义
拟阵M是一个二元组(I,R),其中I是一个有限集,R是I的子集簇,R被称为独立集,它满足下列性质:
(1)∅ 是独立集。
(2)遗传性:任意的A′⊂A⊂I,如果A∈R,那么A′∈R。
(3)交换性:如果A∈R,B∈R且|A|>|B|,那么∃e∈AB使得{e}⋃B∈R。
针对划分拟阵(partition matroid),有限集I被划分成m类,类别集合L={L1,L2,…,Lm},独立集R满足为第i个类别划分上的阈值(threshold),该阈值表示推荐结果中至多有Ti个物品来自类别Li。均匀拟阵是划分拟阵的一种特例,即当m=1时,划分拟阵则变为均匀拟阵(uniform matroid)。
把top-k多样性推荐问题转化为一个划分拟阵上的优化问题,利用聚类算法将推荐项聚类到多个类别(划分)中,用户通过界面输入一个阈值,该阈值表示结果集中同一类别内用户最多允许出现的数目,对初始的相关性结果大于阈值的类别进行调整,分配到其他类别上从而使得最终结果能够尽可能覆盖整个类别,并且使得相关性大的类别出现的数目多,相关性小的类别出现的数目少。这里考虑到用户兴趣爱好的变化性,假设所有类别都是用户感兴趣的。
具体地,令推荐项目集为I,I={i1,i2,…,im},其中I被划分成m类。L={L1,L2,…,Lm}为类别集合,例如L2={i2,i5,i8,i10}。用户集合为U,U={u1,u2,…,un}。对于任意用户u,u∈U,top-k个性化多样性推荐的任务是从各个类别中选择满足约束条件的k个元素集合Ru,Ru⊆I,使得目标函数的效益utility(Ru)最大化。
3.2 整体框架流程
如图2所示,PDM框架分为在线和离线两个阶段。其中评分预测和聚类过程运算量较大且能够动态计算更新,因此可以在离线阶段进行线下计算,而在线阶段直接使用离线结果进行计算,从而缩短响应时间,可有效提高用户体验。评分预测过程中,采用基于模型分解的ALS[6](alternating least squares)协同过滤算法完成预测。并根据用户评分数据利用k-means聚类算法将推荐项聚类。在线阶段中,首先根据评分预测结果进行相关性推荐,并利用用户输入的阈值对初始推荐结果进行类别权重,调整后的结果作为非均匀划分拟阵约束施加到PDM推荐模型上,推荐模型将在推荐过程中对用户偏好、相关性和多样性进行计算,最后将生成的top-k多样性结果集合返回给推荐用户。
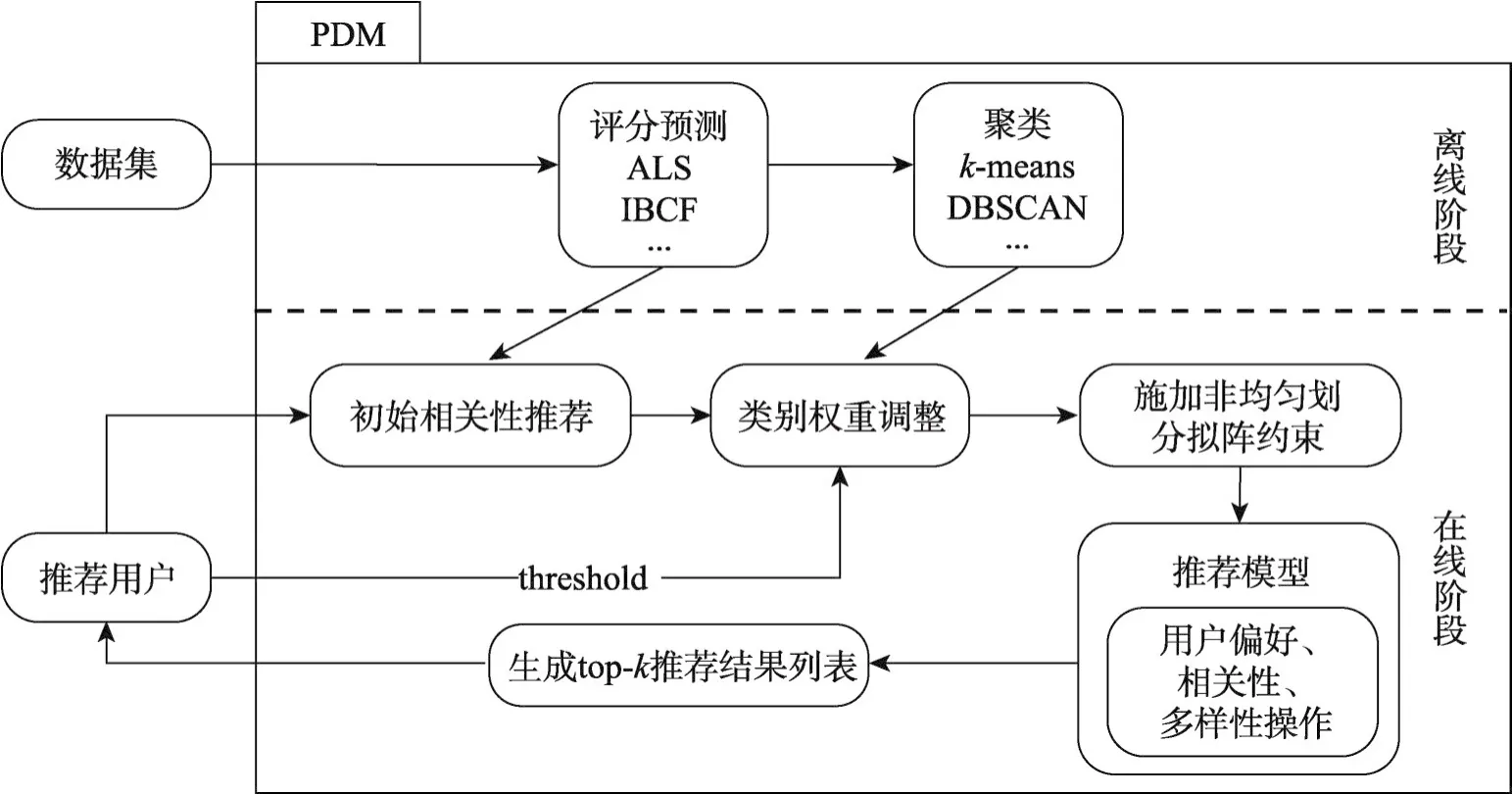
Fig.2 Flowchart of PDM framework图2 PDM框架流程图
3.3 非均匀划分拟阵约束下的多样性模型
假设1用户对推荐项目的评分越高,该推荐项与用户的兴趣爱好越相关。
基于这个假设,为方便表达,首先描述相关定义:
定义1(相关性)用户u(u∈U)对推荐项i(i∈I)的评分记为Scoreu(i),推荐项i与用户u的相关性形式化描述如下:

定义2(集合相似度)集合S的相似度为集合S中两两推荐项目之间的平均相似度,形式化定义如下:
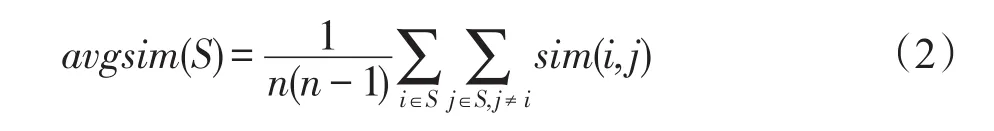
其中,S∈I,n=|S|,sim(i,j)为推荐项i,j∈I之间的相似度,相似度可以采用余弦相似度等度量方法。
定义3(类别内部偏好程度)用户u∈U按照PDM模型进行推荐,推荐结果集记作Ru,推荐项i∈I的类别记为Li;Ru中与推荐项i类别相同的推荐项构成的集合记为,用户u对类别Li的内部偏好(inner preference,IP)记为),形式化定义如下:
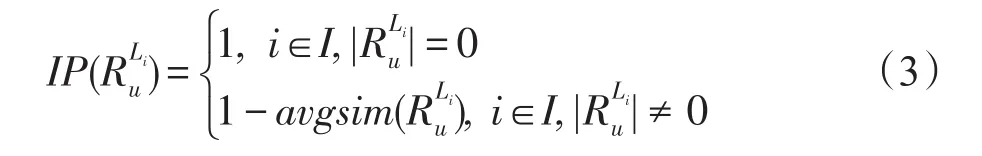
定义4(整体类别偏好程度)用户u∈U按照PDM模型进行推荐,推荐结果集记作Ru,用户u对类别Ru的整体类别偏好(aggregate preference,AP)记为AP(Ru),形式化定义如下:
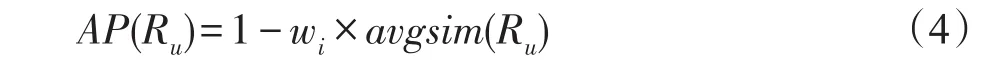
其中,惩罚因子wi控制着与推荐项i属于同一类别的推荐项加入到R中的困难程度,wi越大,对推荐项i的惩罚力度越大,推荐项i加入到推荐列表的困难程度也越大。wi被定义为[13]:

在等式(5)中,Zi表示R中已经包含与推荐项i来自于同一个类别的推荐项数量。
由于用户同时具有不同的偏好,用融合上述两种偏好的乘积作为用户u∈U推荐列表Ru∈I的多样化效用,记为:
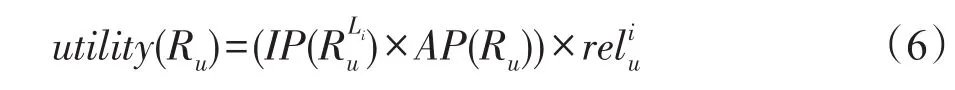
因此,非均匀划分拟阵约束下基于PDM的多样性最大化问题可以定义为:
定义5(多样性最大化)按照PDM进行多样性推荐,给定任意用户u∈U,求解用户u多样性效用最大化的结果集Ru⊆I,使得:
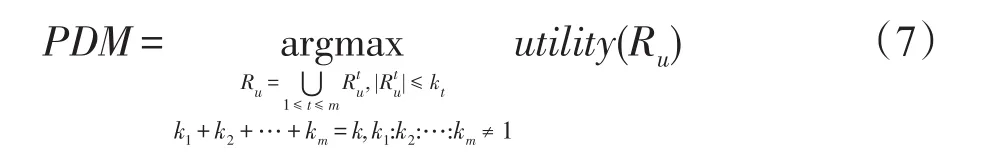
在等式(7)中,实施划分拟阵约束的目的是使推荐列表Ru能够尽可能地覆盖到所有与用户兴趣爱好相关的类别中。本文仅使用了数据中的显示评分信息,没有使用隐示信息,如时间、标题等;根据模型,式(7)中仅对不同类别出现在结果集中的数目以及k值进行约束,依据模型和数据集的不同可以对推荐项的多个属性进行约束。Ru来自于划分中,满足,kt为类别权重调整后各个类别的上限值,值得注意kt的值不完全相同,即k1:k2:…:km≠ 1。
定理1PDM模型的多样性最大化问题是一个关于k的NP-hard问题。
证明在PDM模型中,当用户u∈U对类别内部的偏好程度均相同时,即,i∈I,PDM 模型则退化为Max-sum模型,因此,Max-sum模型是PDM模型的一种特例。文献[13]证明了Max-sum模型下的多样性最大化问题是一个关于k的NP-hard问题,因此等式(7)描述的PDM模型下的多样性最大化也是一个关于k的NP-hard问题。 □
定理2在PDM模型下,任意推荐用户u∈U的推荐结果列表Ru∈I的多样性效用函数utility(Ru)是一个非负、单调、子模函数。
证明任意推荐用户u∈U在PDM模型的推荐过程中,若每次均在整个推荐项集合中进行筛选,那么,推荐过程将按照Max-sum模型进行,最终得到utility(Ru)。由于Wu等[13]已经证明了Max-sum模型的效用函数具有子模性,因此,在PDM模型下,任意推荐用户u的推荐结果列表Ru⊆I的多样性效用函数utility(Ru)也具有子模性。 □
定理3若函数f是一个单调、非递减的子模函数,贪心(greedy)算法获得k个元素的集合SG满足[22]:
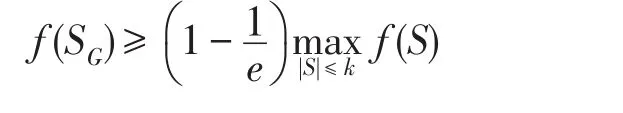
由定义1及定理2结论可知,求解Ru可归结为一个子模函数优化问题。于是,给定任意推荐用户u∈U,在非均匀拟阵约束条件下,以utility(Ru)作为子模目标函数,由定理3和子模函数优化理论[22]可知,使用贪心选择法可得到(1-1/e)的近似保证。
4 非均匀划分拟阵约束下的多样性推荐算法
4.1 初始类别权重调整算法
设不同用户对各个推荐项类别具有不同的初始权重,这些初始权重是根据初始推荐结果计算得到的。具体方法为:取前k个评分最高的推荐项作为用户u∈U的初始推荐结果Ru,统计每个用户的推荐列表Ru中各个类别上的推荐项数量,并将其作为初始权重。例如,R1中有7个推荐项来自类别L2时,则L2W1=7。
如果按照初始类别权重进行分配,由于存在部分类别的权重很大,而其他类别的很小的现象,而且,权重很大的类别可能是用户很感兴趣的类别,而权重较低的类别可能是用户尚未了解、未触及的推荐项,从而导致top-k推荐列表仅来自有数几个与用户兴趣爱好高度相关的类别而不能完整反映整个推荐项的轮廓结构,产品曝光率低。为了更好地提高推荐结果的多样性,在所有类别上施加了非均匀划分拟阵约束,对初始类别权重大于给定阈值的推荐项所属的类别按照算法1进行类别权重调整。
算法1初始类别权重调整算法

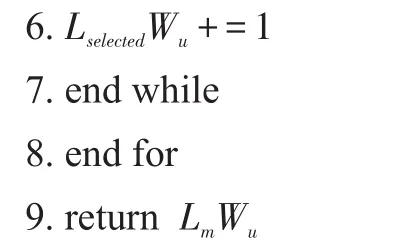
算法1主要涉及3个参数:(1)初始推荐结果InitResult;(2)聚类结果L;(3)阈值threshold。算法首先统计用户初始推荐结果中各个类别的权重,即各个类别在初始推荐结果中出现的数量(第1行),对类别权重大于给定阈值的类别Lm进行如下调整(第2~9行):随机选择权重类别最小的类别(第4行),将其权重类别加1(第5行),同时将类别Lm的权重减1。如此反复调整,直到初始推荐结果的类别权重均小于或等于给定阈值为止,值得注意的是:如果给定的阈值较大,初始推荐结果的类别权重均小于该阈值,则最终推荐结果与初始推荐结果完全相同;相反,如果给定的阈值较小,则每个类别上都要进行相应的调整。
4.2 PDM贪心算法
首先通过一个例子解释PDM算法的逻辑计算。无向带权图G一共有8个顶点,分别是每个顶点都有各自的属性,如,表示顶点v2,来自于类别1。无向图G的邻接矩阵(上三角矩阵)如表1所示,权重表示顶点之间的相似度,而相关度可以利用等式(1)计算得到,无向图G中顶点之间的相关度如表2所示。
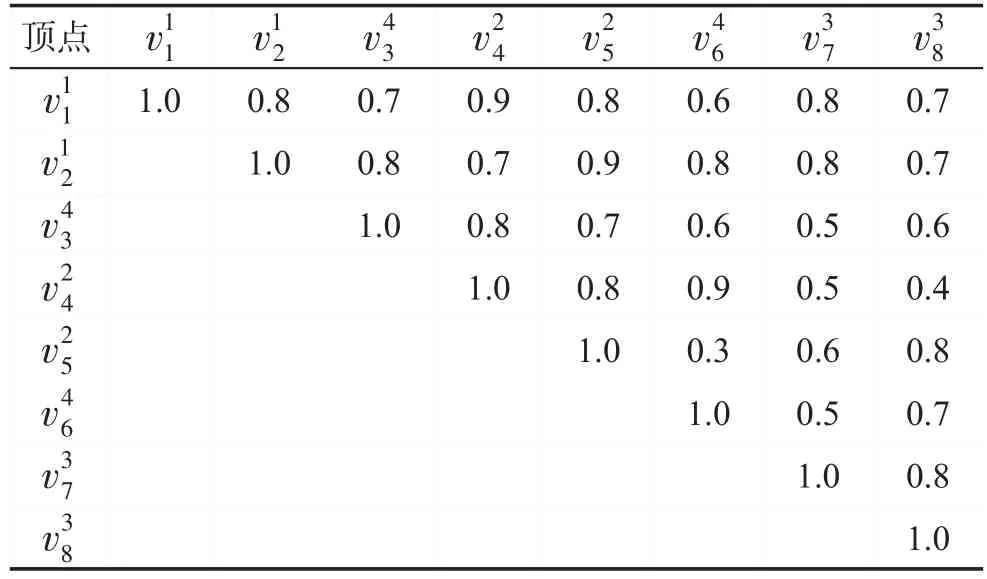
Table 1 Adjacency matrix of graph G表1 图G的邻接矩阵
利用贪心算法求解满足PDM多样性的前6个检索结果,输入查询为顶点,设用户输入的阈值为2,对初始的相关性检索结果进行类别权重调整后的权重如表3所示:允许类别1中的顶点在结果集合中出现2次;允许类别3中的顶点在结果集合中出现1次。
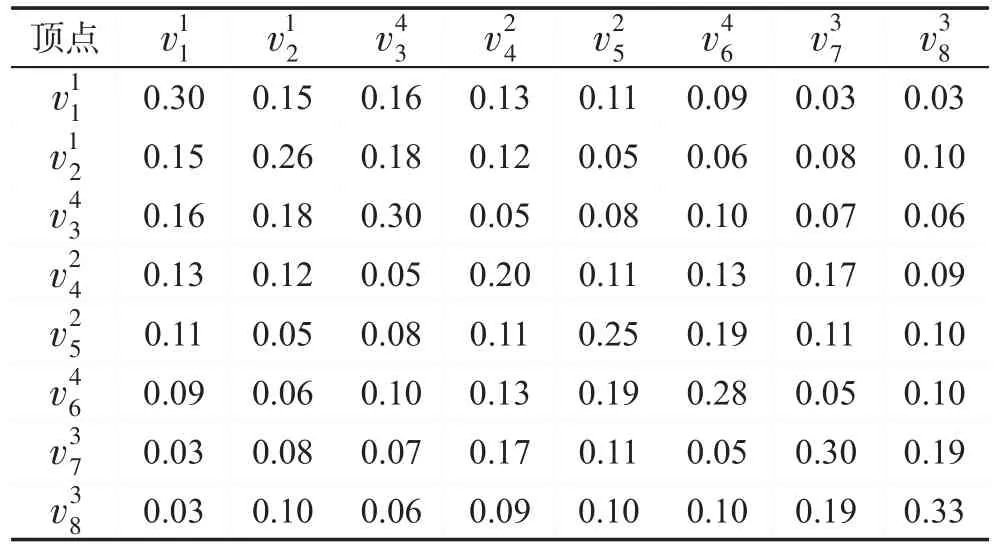
Table 2 Relevance of vertex in graph G表2 图G中顶点之间的相关度

Table 3 Adjusted category weights表3 调整后的类别权重
在类别2内的顶点分别与R中的顶点计算PDM效益。对于顶点:PDM值为(1-((exp(-(2-0)/2)))×((0.8+0.9+0.7)/3/(3-1)))×1×0.13=0.110 9。对于顶点:PDM值为(1-((exp(-(2-0)/2)))×((0.8+0.8+0.9)/3/(3-1)))×1×0.11=0.093 1。由于,故先将加入R中,
采用同样的方式计算后的最终推荐结果为R=
通过上面具体的逻辑计算,可以得出算法2的关键步骤。算法2涉及到用户u∈U对所有推荐项的评分和类别权重LmWu两个参数。算法首先进行初始化工作(第1~3行),接着算法先更新wi、Zi(第4行),对调整后的每个类别(第6行),在类别簇内计算PDM值,将使PDM最大的推荐项加入R中,同时更新变量(第7~15行)。
PDM贪心算法包括在线阶段初始类别权重调整和生成检索结果两个步骤。算法1中主要涉及类别权重调整,最坏情况下top-k来自于同一类别,因此,算法1的时间复杂度为O(k);将推荐项集合I={i1,i2,…,in}的大小记作n,算法2的关键迭代步骤为第5~7行,最坏情况下L的长度为k,|Ri|的长度为1,因此时间复杂度为O(kn),由于算法2是在类别簇内局部贪心,而不是每次都在所有推荐项中进行全局贪心,因此空间复杂度为O(n)。从算法角度看,施加非均匀划分拟阵约束后,算法的时间复杂度从O(k2n)降为O(kn),空间复杂度也从O(kn)下降为O(n)。
算法2PDM贪心算法

5 实验与结果
实验执行环境为Intel Core i7处理器,8Cores,每个Core的主频为3.4 GHz,Windows 10 64 bit操作系统,12 GB内存。实验程序基于Pandas模块,采用Python2.7版程序设计语言实现。
5.1 基线算法
为了比较最终的多样性推荐效果,实现了下面四种算法:
(1)PDM:本文第4章中提出一种非均匀划分拟阵约束下基于偏好的多样性近似优化算法。
(2)Max-sum:文献[13]提出一种多样性图像检索近似优化算法。
(3)PDRank:文献[2]基于异质学术网络提出一种融合作者、论文权威度和多样性的推荐方法。
(4)GraphRec:文献[4]基于社交网络提出一种面向“两阶段”重排序的多样性图排序算法。
5.2 数据集
从用户数目、推荐项数目、评分数目、评分范围和稀疏度五方面描述数据集MovieLens(http://grouplens.org/datasets/movielens/)与 Book-Crossing(http://www2.informatik.unifreiburg.de/~cziegler/BX/)。 由 于内存限制,对Book-Crossing数据集进行缩减,筛选这些用户和推荐项:对20个及以上的推荐项进行打分的用户和被10个及以上用户打过分的推荐项。经过筛选后剩下的数据集记作Remaining Book-Crossing,缩减后的Book-Crossing数据信息如表4所示,没有使用数据集中提供的隐式信息。
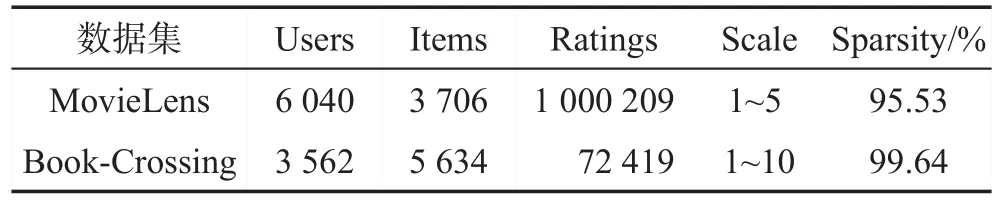
Table 4 Detail information of dataset表4 数据集详细信息统计
5.3 多样性与准确度度量
在推荐系统中,针对不同角度的多样性存在不同的度量方式。文献[12]列举出不同的多样性度量方法,其中,Hurley等[11]、Aytekin等[5]和Bradley等[21]描述了一种能有效度量特定用户推荐列表多样性的方法。该方法计算用户推荐列表中两两推荐项相异度的平均值,定义如下:
设I={i1,i2,…,in}为所有推荐项的集合,U={u1,u2,…,un}是全部用户的集合,那么用户u(u∈U)的推荐列表Ru⊆I的多样性Div为:
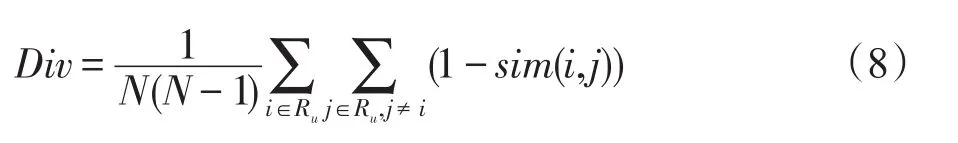
其中,sim(i,j)是推荐项i,j∈I的相似度,N为推荐列表的长度。
尽管等式(8)是一种合理的多样性度量方法,但是仅仅考虑推荐列表的不相似度不能更完整地反映推荐结果的多样性。比如,尚未考虑推荐结果的类别覆盖度。Vargas等[19]利用概率方式从类型覆盖度和类型非冗余度两方面衡量推荐列表的多样性,其被定义为:
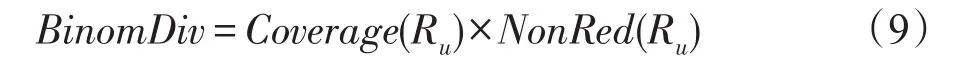
这是一种新颖的度量方法,但只结合类型这一单一因素[12]。受此启发,提出一种新颖的多样性度量方法DisCoverDiv,形式化表示为等式(10):
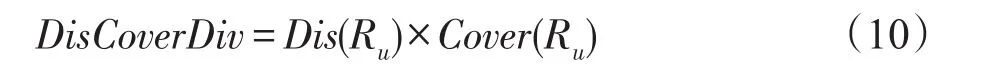
其中,Dis(Ru)为推荐结果Ru中两两推荐项之间的不相似度,可以通过等式(8)获得,Cover(Ru)是推荐结果Ru所覆盖的类别数目|C(Ru)|占推荐列表长度|Ru|的比例,其被描述成等式(11):
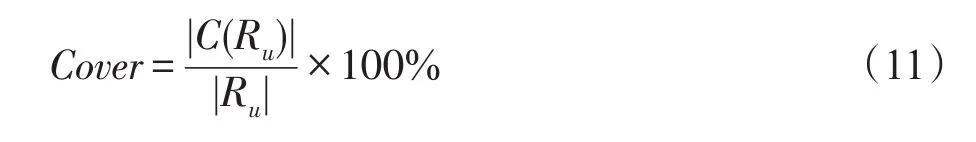
准确率(Precision)作为衡量结果准确度的标准在推荐系统[8]等领域有着广泛的应用,利用准确率评价top-k推荐列表的准确度,其定义如下:
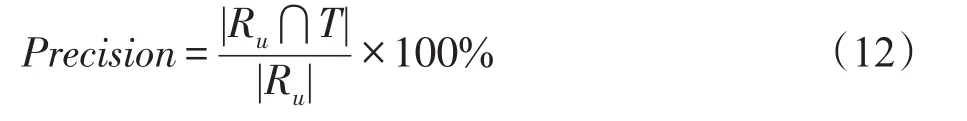
其中,Ru为用户u∈U的推荐结果列表,T⊆I为用户u评过5或10分的商品集合。在准确度度量中,假设用户对推荐项的评分越高,该推荐项与用户兴趣的相关度也越高。基于此,仅选择用户评过满分5分(MovieLens数据集)或10分(Book-Crossing数据集)的推荐项进行测试。正如文献[5]中提到,这种做法往往会比真实的准确度低。
5.4 实验结果
将PDM贪心算法分别应用到MovieLens、Book-Crossing两个真实的数据集上进行实验。首先,观察了多样性和准确率随着阈值变化的影响。实验中推荐列表长度k=20,聚类数目m=20,随机采样500个用户进行多次重复实验。实验结果如图3、图4所示。在不同数据集上,当每个类别上给定的上限阈值较大时,初始推荐结果中的类别权重均小于给定的阈值,因此不再需要调整,最后的推荐结果与初始推荐结果一致,图像基本保持不变,多样性较低,但此时的准确度较高;随着阈值不断降低,初始推荐结果中的类别权重开始重新调整分配,将大于阈值的部分分配到权重最小的类别上,最终推荐结果的多样性逐渐增大,与此同时,准确度也随之降低。如图5所示,这也客观地反映了多样性与准确度之间的对立关系:准确率伴随多样性的提高而降低。
其次,还与三种基准算法Max-sum、PDRank、GraphRec进行比较。本次实验,观察不同方法下多样性和准确度随推荐列表长度top-k的变化情况。同样地,随机采样500个用户进行多次重复实验,实验结果如图6~图9所示:从图中可以看出,随着top-k逐渐增大,四种方法的多样性和准确度都逐渐降低。

Fig.3 Change of diversity with different thresholds图3 多样性随阈值的变化情况

Fig.4 Change of precision with different thresholds图4 准确率随阈值的变化情况
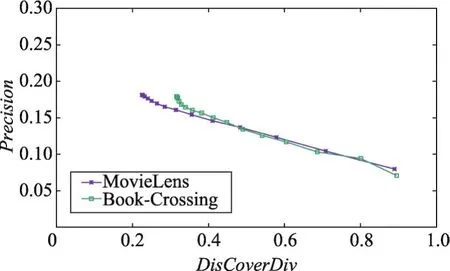
Fig.5 Relationship between precision and diversity图5 多样性与准确率之间的关系
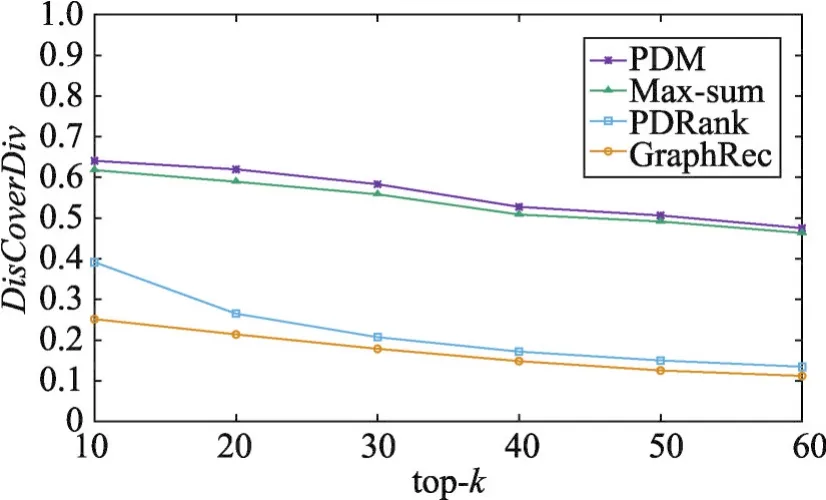
Fig.6 Change of diversity with top-k(MovieLens)图6 多样性随top-k的变化情况(MovieLens)
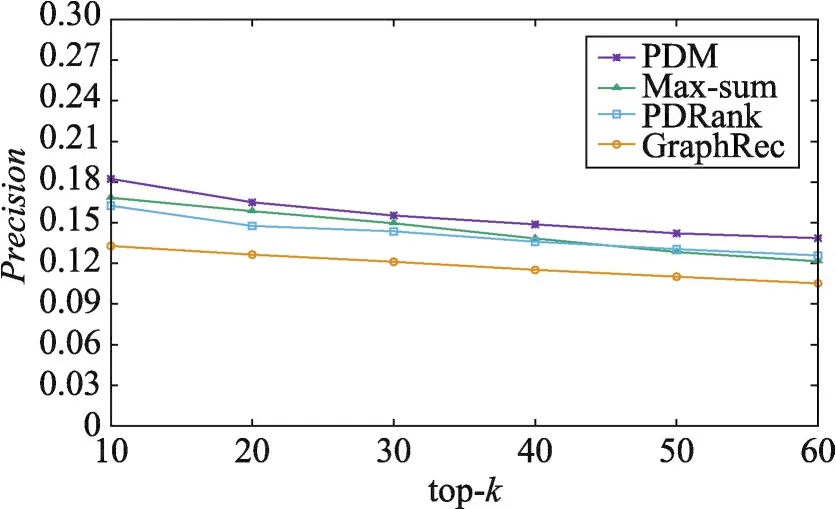
Fig.7 Change of precision with top-k(MovieLens)图7 准确率随top-k的变化情况(MovieLens)
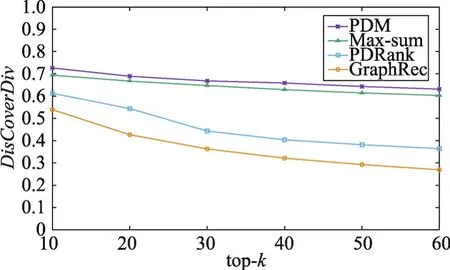
Fig.8 Change of diversity with top-k(Book-Crossing)图8 多样性随top-k的变化情况(Book-Crossing)
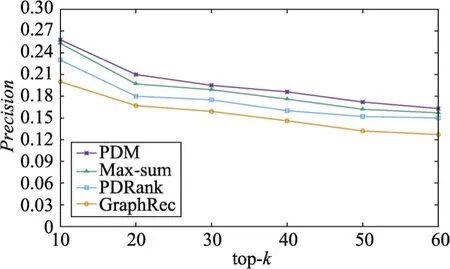
Fig.9 Change of precision with top-k(Book-Crossing)图9 准确率随top-k的变化情况(Book-Crossing)
此外,针对那些对推荐项打分较少的用户,以及被较少用户打了分的数据进行相同的实验,结果如图10、图11所示,实验表明所提出的方法在该数据集上仍然能够获得较好的折中效果;对比图9、图11,Remaining Book-Crossing数据集上的准确度相对较低,主要原因在于较高的稀疏率(99.97%)导致预测评分阶段的误差率升高。

Fig.10 Change of diversity with top-k(Remaining Book-Crossing)图10 多样性随top-k的变化情况(Remaining Book-Crossing)
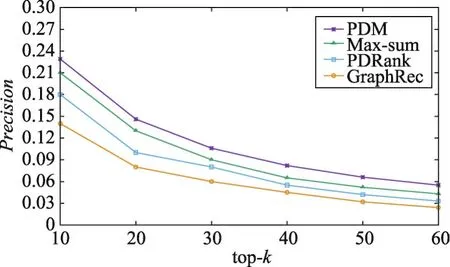
Fig.11 Change of precision with top-k(Remaining Book-Crossing)图11 准确率随top-k的变化情况(Remaining Book-Crossing)
由于在PDM、Max-sum方法上均施加了划分拟阵约束,它们的多样性效果优于其他两种方法。然而,PDM方法不仅考虑了用户对不同类别的偏好程度,而且还考虑了不同用户对推荐列表中相同类别内部多样性的偏好程度,因此本文提出的PDM方法在多样性和准确度两方面均优于其他三种方法,并且能够获得更好的折中效果。
再次,报告了四种不同方法生成推荐列表中类别的召回率。如表5所示:根据前面的分析,由于在PDM、Max-sum方法上施加了非均匀拟阵约束,因此它们在类别簇上的召回率是相同的,且能够覆盖更为广泛的类别。而PDRank、GraphRec两种方法由于受到均匀拟阵约束,推荐结果仅来自于查询用户兴趣相关的少数几个类别中,因此这两种方法推荐结果的类别召回率相对较低。
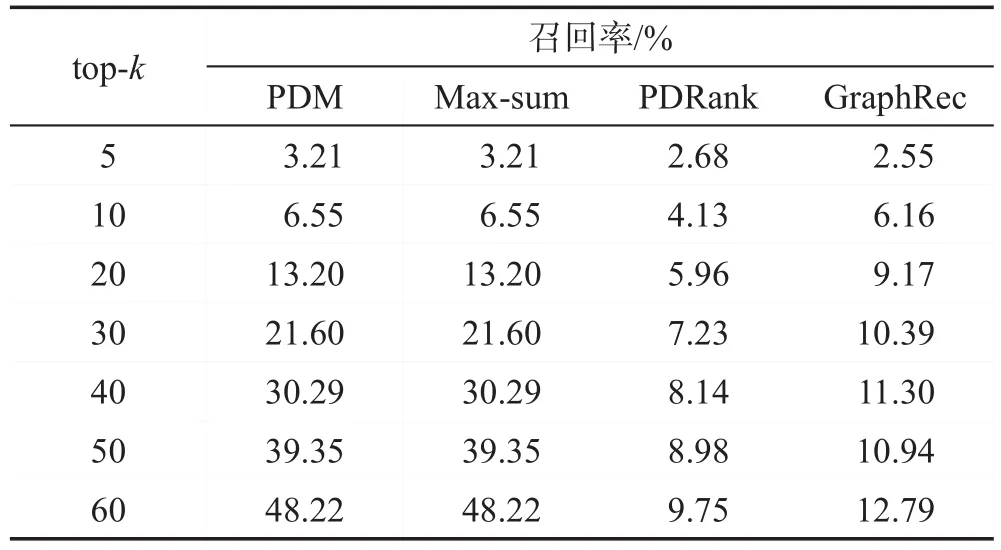
Table 5 Category cluster recall表5 类别簇上的召回率
最后,还进行了一些重复实验来比较四种不同多样性推荐算法生成多样性推荐结果所需的时间。如表6所示:记录了为一个用户生成不同长度的多样性推荐结果所需的平均时间,PDM、Max-sum、PDRank三种算法在推荐过程中都同步考虑了推荐结果的多样性和相关性,生成最终结果相对耗时,而GraphRec算法则分为两个阶段进行,第一阶段进行相关性排序,第二阶段在相关性排序结果的基础上进行多样性排序。最后选择排名靠前的k个结果作为最终推荐结果,该算法主要为内排序操作,速度较快。不同于Max-sum算法,PDM算法通过在类别簇内局部贪心选择该类别中满足PDM模型的结果,而不是在每次贪心选择均要遍历整个推荐项集合,因此PDM算法比Max-sum算法耗时更短。
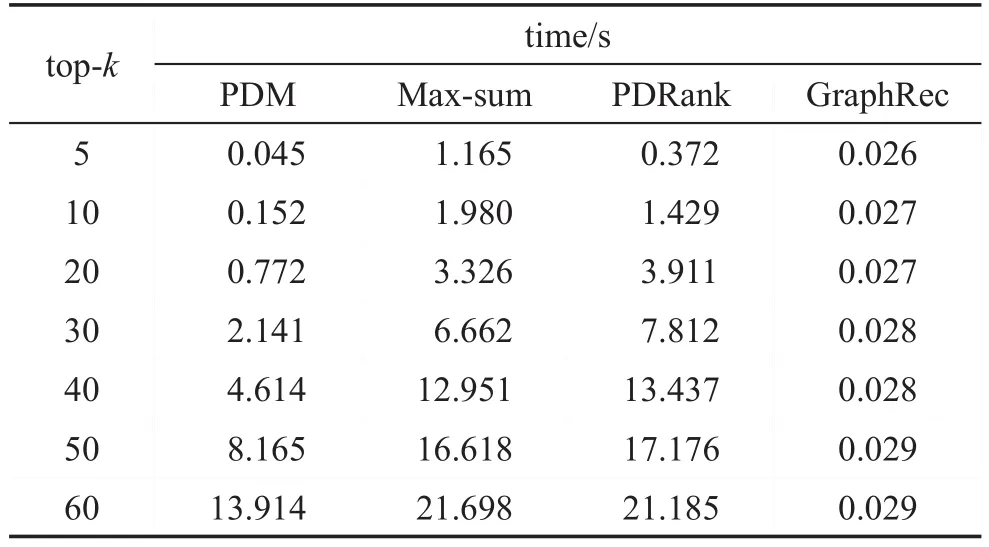
Table 6 Time to generate diversified recommendation result for a user表6 为一个用户生成多样性推荐结果所需的时间
6 结束语
本文主要研究了个性化推荐中的多样性推荐问题,针对现有多样性方法的不足,提出非均匀划分拟阵约束下的多样性最大化问题,并将多样性最大化问题建模为非均匀划分拟阵约束下的子模函数优化问题,提出了一种基于用户偏好的多样性推荐算法PDM。算法的多样性不仅考虑用户偏好能够覆盖广泛的类别,而且也考虑相同类别中偏好冗余程度小、差异性较大的推荐,最后设计了贪心算法求解该问题。不同数据集的实验结果证明了提出方法的可行性,能够在多样性和准确度上取得良好的折中效果。在进一步工作中,将结合推荐项的显式评分和隐式内容采用机器学习方式深入挖掘基于大数据背景下的有效信息和高效率的多样性推荐方法,比如,如何更加智能地设置阈值等。
