结合深度学习的网络邻居结构研究及应用*

寇晓宇，吕天舒，张 岩

北京大学 信息科学技术学院，北京 100871

1 引言

随着信息网络规模的急剧增大，网络数据变得复杂多样，通过分析和研究网络的拓扑结构，可以探索到网络中丰富的知识，进而可以提炼出多种高效的营销模式。如在微博、Facebook为代表的社交网络中，一种方式是通过已知的好友关系以及部分属性已知的用户推测出未知用户的属性，进一步得到用户在不同属性类别下的影响力高低，从而利用网络中具有高影响力的用户进行高效营销；另一种方式是通过预测某用户未来的行为，有针对性地进行个性化营销等。

网络中节点的邻居结构可以描述节点间的复杂交互关系，不同的邻居结构往往有不同的意义表达。如微博中用户的关注关系，若某明星A自身有大量粉丝，并且A关注了B，一般情况下，B也是明星或者有高影响力的用户；若A的大量粉丝没有任何粉丝，一般情况下说明A有大量“僵尸粉”但实际影响力不高。目前对于网络拓扑关系的研究中大多数关注直接邻居组成的结构情况[1-2]或者不同跳数邻居的数目情况[3]，很少关注不同跳数邻居组成的结构的影响。为了解决这一问题，本文以三种最为基本的邻居结构进行分析。图1给出一个实例，红色节点为目标节点，邻居A、B为指向目标节点的直接邻居，构成两个第一种邻居结构；邻居C、D构成一个第二种邻居结构，其中邻居D为目标节点的二度邻居；邻居E、F构成一个第三种邻居结构，其中邻居F既是目标节点的一度邻居，也是二度邻居。因为这三种邻居结构最为普遍，而且比较有代表性，既包含简单交互关系，也有复杂交互关系，因此选取这样三种邻居结构进行实验。

网络中邻居形成的不同结构有着不同的影响效果：例如在使用微博转发的数据集进行用户行为预测时，要判断图1的红色节点即目标用户V是否会去转发微博t，V的好友们构成了这三种邻居结构。若仅仅好友A或好友B转发了t，对V触动可能并不大；若t接连被D和C转发，V会有更大的可能性继续转发t；若当t接连被F和E转发，且E和F有共同好友V，则V也转发t的可能性更大。

自然语言处理技术与深度学习算法在网络中的应用越来越广泛，如网络表示学习的DeepWalk模型[4]通过随机游走得到节点序列，最终得到节点向量表示。同时深度学习算法促进了特征自动提取的实现，本文通过结合深度学习卷积神经网络（convolutional neural networks，CNN）[5]对网络进行研究。由于直接将邻居结构输入到CNN中处理会大大降低运行效率，且CNN更适应于处理图像数据，因此可以将邻居结构数据转换为图片的格式，提高CNN对数据处理的速度。

本文的主要贡献包括：

（1）提出了结合深度学习CNN的网络邻居结构影响力模型DNSI（neighbor structure influence based on deep learning），并通过自动特征提取的方式得到三种邻居结构在网络中的影响力大小。

（2）将邻居结构数据转换为便于CNN对网络数据处理的样式，即将网络中节点的不同类别下三种邻居结构矩阵数据转换成图片的像素值，输入到CNN中进行批量处理。

（3）由模型DNSI得到三种邻居结构的影响力，在真实世界的网络数据集上进行节点属性预测、类别中心度度量以及用户行为预测，证明该模型在绝大多数情况下都可以提高预测的正确率。

本文第2章介绍使用拓扑结构对网络进行分析的相关研究。第3章详细介绍了本文提出的基于深度学习的网络邻居结构影响力模型DNSI的原理。第4章为模型在多个真实世界数据集上的实验结果。最后，是对本文工作的总结和下一步工作的展望。

2 相关工作

本章介绍基于拓扑结构对网络分析的相关研究，包括传统的基于拓扑结构进行的网络研究以及融合深度学习与拓扑结构的网络研究两部分。

2.1 传统的基于拓扑结构进行的网络研究

（1）对用户属性预测

针对社交网络中用户会选择性提供个人信息的情况，He等人[6]提出将好友关系映射出贝叶斯网络的方法，通过已知的先验概率对用户属性进行推测，可以得到预测为每种属性的条件概率。而Zhou等人[7]在这基础上融合了用户的社交关系，指出不同的社交关系可以推测不同的属性。Zheleva等人[8]拓展了社交关系，通过可见的群信息来推测用户属性。除此之外，Mislove等人[9]提出了基于社区发现的推测用户属性算法，该算法可以应用于在线社交网络，算法思想是相同属性的用户更有可能形成聚合度比较高的社区群体。

（2）中心度度量

最常见也最容易理解的中心度度量指标为度中心性（degree centrality）[10]，定义为目标节点的直接邻居数目，该指标反映出该节点的直接影响力情况。Chen等人[11]将中心度扩展到目标节点的邻居数目与其邻居的邻居数目，即局部中心性（local centrality）指标。在这种思想的引领下，扩展度（ExDegree）指标指出，不同的节点传播概率，会有不同的度扩展层数，比如：n节点传播概率很小，则只需计算直接相邻的邻居数目，而m节点概率较大，则可能要计算三度以内邻居数目，且一度邻居数目计算三次，二度邻居数目计算两次，三度邻居节点只计算一次。在此基础上，Fowler等人[3]定义节点的三度以内的邻居都属于强连接关系，三度以上的邻居不会被影响，即三度影响力原则。

另两个常见的反映节点拓扑特性的指标是介数中心性（betweenness centrality）[2]与紧密中心性（closeness centrality）[12]，介数中心性是指目标节点在网络中任意两个节点的最短路径上的数目，紧密中心性是指某节点到达网络中所有其他节点的总距离除以步数。由于这两个方法复杂度都比较大，不适合于大型的网络，因此人们提出很多改进方法，如Kitsak等人[13]提出的K-核分解算法，通过把网络中所有节点从核心到边缘分层，来定义影响力的大小。而Lv等人[14]通过研究提出H指数（对期刊或者作者进行影响力评价的指标）与K-核在衡量节点影响力方面有类似的效果。

（3）用户行为预测

对社交网络中用户行为的分析最早出现在复杂性科学、统计物理等领域，如Zhou等人[15]进行人类行为特征的研究综述。除此之外，Zaman等人[16]利用协同过滤方法，通过对博客的用户转发数据集进行分析，从而得到用户转发的概率。受到上面这些思想的启发，Tang等人[17]深入研究了微博上用户的转发数据，剖析邻居节点形成的拓扑结构，发现已转发过某消息的邻居节点形成的连通图个数会对目标节点产生影响，从而提出局部节点影响力（social influence locality）模型，并证明在已转发某消息的邻居数目相同的情况下，形成的连通子图数目越少，目标节点也转发该消息的可能性就越大。进而又提出在动态网络上不同的邻居结构对目标节点的行为有不同的影响力，即StructInf模型[18]，并通过对微博数据的边采样和节点采样，得到了20种邻居结构的影响力。本文中的模型便是受到StructInf模型的启发，对其邻居结构进行分类简化，使用深度学习得到邻居结构影响力，并对其应用范围进行了扩展。

2.2 融合深度学习与拓扑结构的网络研究

2.1节所述的相关研究由于受到特定因素的影响，会有一定局限性，比如网络规模较大、网络结构变化大等因素。如StructInf模型需首先进行边采样和节点采样，然后通过统计方式计算其邻居结构影响力，计算量庞大。而随着深度学习的深入人心，将深度学习算法融入传统网络拓扑结构的研究不断涌现，相比较传统的网络研究方法，其优越性一方面体现在准确率的提升，另一方面体现在算法运行速度的提高。如DeepWalk算法[4]在自然语言处理的启发下，通过在网络中随机游走地选择节点与边，把网络转换成一系列“句子”，其中单词代表节点，从而可以利用自然语言处理中的skip-gram模型[19]，将单词（节点）转换为表示向量，进而对网络分析。LINE模型[20]在DeepWalk的基础上，融合了节点的邻居结构，提出网络中存在的两种相似性，第一种是first-order，即两个节点直接有边相连则为相似；第二种是second-order，即两个节点的共享邻居数目越多，相似性越高。通过两种相似性学习得到的两种向量表示的拼接，可以得到节点的特征表示，从而可以进行网络研究。

3 基于深度学习的邻居结构影响力研究

本文提出基于深度学习的网络邻居结构影响力模型DNSI，该模型利用CNN算法进行特征提取，得到三种邻居结构的影响力，从而进行节点属性预测、类别中心度度量以及用户行为预测三类实验。本章首先给出模型相关定义，然后详细介绍模型的实现，并进行实例讲解，最后对模型的复杂度进行讨论与分析。

3.1 相关定义

该模型首先统计出网络中所有节点的三种邻居结构的数目，输入到CNN中构建深度网络，通过特征提取得到三种邻居结构的影响力，根据这三种影响力可以反映节点在不同图中的不同特性。

定义1（网络图）记G=(E，V)表示一个有向网络图，其中V代表节点v的集合，即V={v1，v2，…，vn}，E代表边ei，j的集合，即所有从节点vi指向节点vj的边集合为E={ei，j}。记f:vi→cj表示一个映射函数：节点vi的类别为cj，D={f1，f2，…，fn}表示节点的类别映射函数的集合，C={c1，c2，…，cn}表示C为所有类别的集合，其中|C|＜＜|V|。

节点的类别在现实世界数据集中有多重解释，例如：在生物数据集中，类别可以代表不同的种群；在用户关注数据集中，类别可以代表用户不同的属性；在微博转发数据集中，类别可以代表用户不同的行为等。

定义2（一度邻居结构）在有向图G=(E，V)中，记目标节点为vn，若vn的直接前驱点vi没有任何前驱，则vi构成一度邻居结构。本文中一度邻居结构对目标节点的影响力记为w1，类别都为cj的邻居构成的一度邻居结构的个数记为mj，1。

定义3（二度邻居结构）在有向图G=(E，V)中，记目标节点为vn，若vn的直接前驱点vi的前驱vj不指向vn时，则vi与指向vi的前驱节点vj组成了二度邻居结构。本文中二度邻居结构对目标节点的影响力记为w2，类别都为cj的邻居构成的二度邻居结构的个数记为mj，2。

定义4（加强二度邻居结构）在有向图G=(E，V)中，记目标节点为vn，若vn的直接前驱点vi的前驱vj也指向vn时，则vi与指向vi的前驱节点vj组成了加强二度邻居结构。本文中加强二度邻居结构对目标节点的影响力记为w3，类别都为cj的邻居构成的加强二度邻居结构的个数记为mj，3。

3.2 模型描述

记需要预测类别的目标节点为vn，其真实类别为ck，且整个网络图G中的类别总数|C|，则模型目的是学习出最合适的w1、w2、w3，使得vn被预测为自身类别ck的概率最大，即本模型的总体优化目标函数为：

P表示当三种邻居结构权重为w1、w2、w3时，vn类别预测为ck的概率，即最大化属于第ck类的邻居构成的三种结构数目与三种影响力的内积和与其他类别cq邻居结构数目与影响力的内积和的差值，具体公式如下所示：

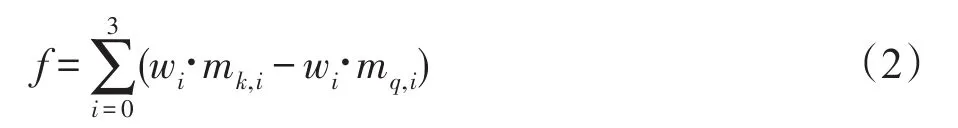
其中，mk，i指属于第ck类的邻居组成第i种结构的数目，同理mq，i指属于第cq类的邻居组成第i种结构的数目。从而使得节点被预测为自身真实类别的概率最大。

整个模型主要分为两部分，经过前两种算法可以得到三种影响力，第三种算法是对节点属性预测，第四种算法是对节点进行类别中心度度量。

算法1三种邻居结构数目的确定

算法1中第4行的L存储了目标节点不同类别的前驱节点；第7行设置flag以及第13行和16行的remove的原因是确保每个邻居节点只能参与到一种邻居结构中。

算法2数据处理与CNN网络层的构建

算法2中第1～5行把节点邻居结构数目矩阵转换成一张张图片的格式，可以加快算法处理速度。第4行说明每张图片的长为|C|个像素，宽为3个像素。第6行得到CNN的输入，X可以看作以图片的形式表示的数据集的特征，Y是每个节点的类别，即数据集的标签。第7行按照给定的切分比例分出训练集和验证集，第8行构建CNN网络，共1个卷积层，3个全连接层，kernal设置为1×3，网络其他具体参数在实验部分讨论。第10～14行定义批处理函数，每次迭代过程中按批次取数据，然后进行交叉验证得到最高的准确率时的卷积层的kernel值，即为三种邻居结构的影响力。

算法3对网络节点类别的预测

算法4类别中心度度量

例如图1中所示的一个有向图G，红色的为目标节点vn。已知有6个邻居节点A、B、C、D、E、F，组成了两个一度结构，1个二度结构，1个加强二度结构，若G中|C|=3，分别为0类、1类、2类，且vn的真实类别是2类。0类在图中是橘色，1类为蓝色，2类为绿色。则根据算法1可得，Q[vn][0]=[2，0，0]，Q[vn][1]=[0，1，0]，Q[vn][1]=[0，0，1]，若已知根据算法 2 得到的w1、w2、w3为[1,2,3]。若进行类别的预测，则根据算法3可得，P[vn]=[2，2，3]，则c′=2 ，即目标节点被预测为2类。若是进行类别中心度度量，则根据算法4可得，T[vn]=[2，2，3]，即目标节点在第0类的中心度为2，在第1类的中心度为2，在第2类的中心度为3。

3.3 复杂度分析

算法的复杂度分析分为时间复杂度与空间复杂度。本模型主要是要保存所有节点的三种邻居结构的数目，因此空间复杂度主要受网络中节点数目影响，即O(|V|)。时间复杂度需要对四种算法分别分析：

算法1的时间复杂度为O(|E|×|V|×|C|)，因为算法需要循环所有节点进行计算邻居情况，计算每个节点的邻居情况时只需要循环一遍网络所有的边并分别保存在不同的类别下即可。又因为类别数|C|是一个较小的常数，所以算法1的时间复杂度可以看作是与节点数与边数乘积成线性相关的。

算法2的时间复杂度为O(k×|V|×|C|)，其中k指CNN网络层的参数对网络的影响，若层数增加或者增加批量训练数据的大小就会有相应影响，但是主要还是受节点数目的影响。其次，Batch_size和Epoch的正确选择也影响内存效率与内存容量之间的平衡。

算法3和算法4的时间复杂度都为O(|C|)，对于每个节点来说，时间复杂度是常数。若是整个网络所有节点计算的话，时间复杂度即与节点数目成线性相关。

4 实验结果

本章首先介绍模型的参数设置以及对比算法，其次是评价指标和数据集介绍，最后在多个真实网络数据集上进行分析实验，并进行参数敏感性分析。

4.1 实验设置

通过在真实网络数据集上实验发现，节点数目少于1 000个时，学习率大小、批处理大小等都应相对减少，权重初始化的方式也应变化。多次实验后得到表1中最优的参数设置，即算法2中构建CNN的具体参数。表中第二行是指在网络中节点数目大于等于1 000个时使用的参数集合，第三行是指节点数目小于1 000个时使用的参数集合。

Tabel 1 Parameter setting in algorithm 2表1 算法2中的参数设置

对于模型将要处理的三类任务，将分别与不同的算法进行对比，其中主要包括下面几种算法：

（1）KNN算法：该方法是机器学习算法的一种，根据最接近目标节点的k个邻居情况来判断目标节点的类别，预测目标节点的类别为占比例最大的邻居类别。

（2）ExDegree算法：扩展度算法，不同的传播概率需计算不同的层数的邻居节点数目，将对不同类别的邻居分别进行统计。本次实验中将采用原始论文中的参数，传播概率0.01到0.15之间，最大扩展度为8，30次独立实验取平均结果，节点将被预测为其中概率最高的类别。

（3）StructInf算法：邻居结构影响力算法，使用作者公布的源代码，按照原始论文中的采样参数，q=0.9，px=0.6，py=0.1，先得到20种邻居结构的影响度，然后对未知用户的行为进行预测。

（4）DeepWalk算法：通过在网络图中进行随机游走得到节点序列，输入到skipgram模型中得到节点向量表示，并进行多标签预测任务。全部使用原始论文中默认的参数进行实验。

4.2 评价指标与数据描述

本次实验包括三部分，分别使用不同的评价指标。

（1）节点属性预测

该任务使用正确率（Accuracy）与平均准确率（mean average precision，MAP）作为评价指标，分别定义如下：

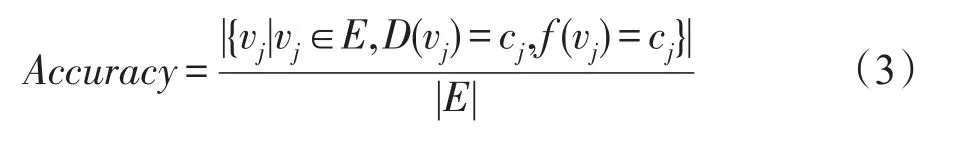
其中，f(vj)是指vj被预测为哪一个属性，D(vj)指vj实际上为哪一个属性，分子表示属性被预测正确的节点。正确率表示为预测正确的节点数目与网络所有节点数目的比值。

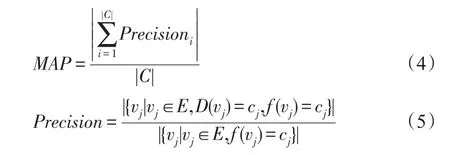
其中，Precisioni表示某个属性被预测正确的节点数目与所有被预测为该属性的节点数目的比值，则MAP表示所有属性准确率的和与网络中属性类别总数的比值。MAP指标目的是为了弥补网络中很多节点由于缺少前驱节点而导致正确率较低的现象。

（2）类别中心度度量

该任务使用算法总运行时间Time与平均前k召回率M_Recall@k作为评价指标，平均前k召回率定义如下：

其中，index(vj)是指节点按照预测的中心度从高到低排序的序号，则Recall@k指模型得到的cj类别的前k个节点中真正属于高中心度节点的个数。num_g指针对某个数据集已知的高中心度的节点数目。则平均前k召回率指所有类别的Recall@k的和与num_g比值。

（3）用户行为预测

该任务使用正确率（Accuracy）、平均准确率MAP、时间Time、最大加速比MRa作为评价指标，其中MRa指其他算法与本实验中模型运行时间的比值的最大值。

本实验中使用的数据都为真实世界数据集，包括公开数据集与爬取的微博数据两部分，具体情况见表2。表中“实验”一列的“1”表示进行节点属性预测，“2”表示类别中心度度量，“3”表示用户行为预测。其中，Biological_tim[21]为美国生物数据集；Bcspwer10[21]为美国电网数据；Fpga_dcop1220[21]为电路仿真网络；Facebook_4039[21]为社交网络数据集；Cite（http：//www.nber.org/patents/）为美国专利引用网络的子图；weibo为爬取的新浪微博用户互相关注网络，以及这些用户在10天内发布微博与转发微博的情况（所有的微博都属于“同桌的你”“房价”“雾霾”“华为”四个主题之一，若用户未发布或者转发这四个主题，则类别为“0”，因此共五种类别）。

Tabel 2 Datasets information表2 数据集统计信息

4.3 实验结果与分析

4.3.1 节点属性预测

节点属性预测实验中每个数据集都是选择80%的数据作为训练数据，其他作为测试数据。正确率和MAP指标结果见表3，对于Biological_tim小数据集，参数参考表1中的第3行。其他数据集的参数参考表1中第2行。其中KNN算法使用k=2和k=5分别做实验，较为全面，具有代表性。

从结果可以看出，DNSI模型除了在Biological_tim数据集的MAP和Fpga_dcop1220数据集上的正确率略低于其他模型，其余的效果均好于其他模型。尤其是Bcspwer10数据集上，正确率超过其他几种模型的13%左右，这说明DNSI在对节点属性预测任务上有很好的效果。其中在Biological_tim小数据集上，几种算法的正确率都比较低，通过分析原始数据发现，很多节点缺少前驱节点，因此会出现无法预测的情况。Fpga_dcop1220数据集的效果普遍都比较高，特别是KNN时得到最高正确率，说明数据本身属性和邻居节点属性相关性非常大。而算法KNN中k=5时的结果往往不如k=2时的好，分析认为邻居扩展太大，不同属性的邻居数目混杂造成的误差。

Tabel 3 Node attribute prediction results表3 节点属性预测结果

Tabel 4 Category central metric results表4 类别中心度度量结果

4.3.2 类别中心度度量

类别中心度度量实验使用的是美国专利引用数据集，可以较好地体现DNSI在大数据集上的优越表现。为了高效地召回中心度较高的节点，本次实验只取入度大于100的节点组成的子图作为数据集。其中，取专利的技术领域作为类别，取从1963年开始，前800个被引用次数最高的专利作为真实的高中心度节点，即式（7）中的num_g=800。

与KNN、ExDegree、Betweenness centrality、Closeness centrality四种算法进行对比实验的结果见表4。从结果可以看出，除了在k=40时，绝大部分情况下DNSI算法都可以得到最高的召回率。特别是在k=10时，DNSI算法可以达到10%召回率，说明同其他四种算法相比，DNSI可以更为准确地召回中心度最高的节点，且DNSI算法的运行时间最短，相比于其他的算法有稳定的优越性。

4.3.3 用户行为预测

用户行为预测实验采用爬取的weibo数据。由于微博具有时效性，为了分析三种算法预测的准确性，通过前k天的用户关注网络和转发情况，来预测第k+1～第10天的用户转发情况（其中，2≤k＜10）。首先对weibo数据进行预处理，将转发信息中包含“同桌的你”“房价”“雾霾”“华为”这4个主题的类别设置为“1～4”，其他未转发这4类主题微博的用户行为类别设置为“0”，然后预测用户是否会转发微博以及转发哪一类微博。

DNSI模型使用表1中第2行的参数。StructInf、DeepWalk模型使用原始论文中的参数，并针对算法专门调整数据格式，使用户关系数据和用户行为类别数据适应算法的输入格式，通过前k天的数据得到20种结构的影响概率，从而计算出第k+1～第10天的用户转发不同类别的微博的可能性，取最大的为预测值。

从表5中的结果可以看出，随着k的增长，三种算法的时间都不断增长，但是StructInf算法运行时间普遍较长，DNSI与StructInf算法的最高加速比可达6.43。当k小于6时，DNSI算法的正确率和平均准确率一般都比较高，但是当k大于6时，StructInf算法的正确率普遍较高，但是MAP不如DNSI。而DeepWalk模型的正确率和平均准确率都比较低，可能是受到数据本身的影响，因为数据中有很多节点没有前驱节点，所以在进行多标签分类时结果较差。三种算法的正确率最高就到80%左右，且与MAP的差距比较大，也是由于节点缺少前驱节点的原因。

Tabel 5 User behavior prediction results in weibo dataset表5 微博数据集中用户行为预测结果

六个数据集的三种邻居结构影响力如图2所示。为了使不同数据集的邻居结构影响力可以互相比较，将w1、w2、w3按比例缩放到0～1之间，且w1+w2+w3=1。可以发现，除了facebook数据集的加强二度邻居结构影响力比较低之外，其他数据集都是加强二度邻居结构影响力最高，说明关系密切且进行交互行为比较频繁的邻居组成会对目标节点影响更大。

4.4 参数敏感性分析

本节度量了Batch_size、Learning_rate和Kernelinitialization三个参数对模型的影响。实验过程中，除当前被测试的参数，其他参数均保持默认值，即表1中的第二行。测试任务使用Bcspwer10、Facebook_4039、weibo三个数据集，分别进行交叉验证求平均正确率和平均迭代次数来展示效果。

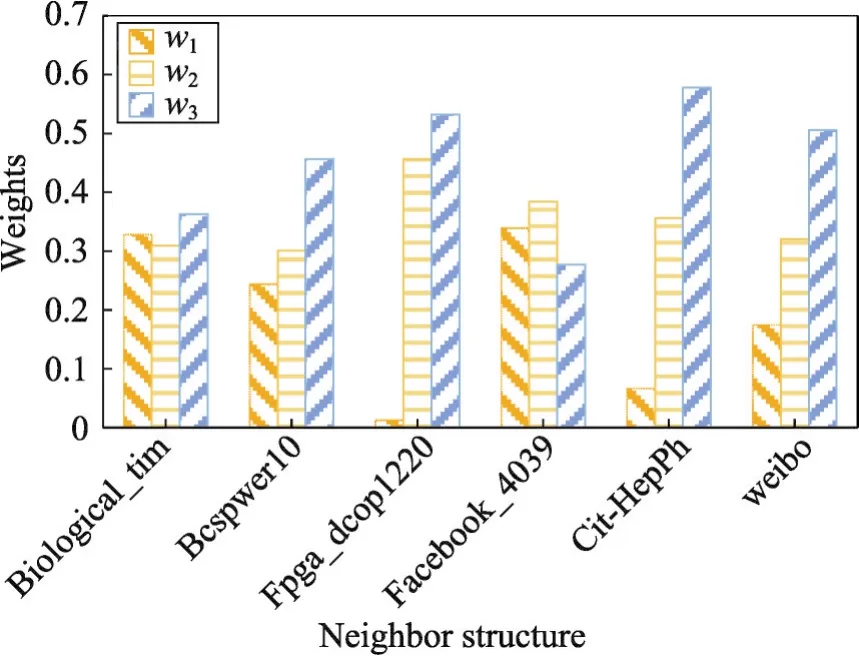
Fig.2 3 neighbor structures'weights of 6 datasets图2 六个数据集的三种邻居结构影响力

首先评估Batch_size对模型的影响，结果如图3所示：Bcspwer10和weibo数据集是随着Batch_size的增加，模型的正确率先升高后降低，在300～500次之间达到最高。原因是：当批处理数据太少时，梯度更新频繁，不容易收敛；当批处理数据过多，梯度的更新难以达到最好的效果。而Facebook_4039数据集在Batch_size为100时达到最优效果，且Batch_size>400后无变化，分析数据发现由于Facebook_4039数据集的类别太多，导致每种类别下的节点数目相对较少，因此当Batch_size>400时，相当于是全部数据一起输入了。

Fig.3 Influence of batch_size on accuracy图3 批处理数据大小对正确率的影响

Learning_rate对模型收敛速度的影响结果如图4所示：当学习率非常小时，模型需要迭代多次才能达到收敛，当学习率在0.01时，模型在三个数据集上迭代的次数都是最少的，而当学习率大于0.01时，模型无法收敛，会出现在极值附近“摇摆不定”的现象。

Fig.4 Influence of learning_rate on DNSI convergence rate图4 学习率对DNSI收敛速度的影响

以Bcspwer10数据集为例分析不同参数组合下权重初始化对模型的影响。第一种权重初始化方式是truncated_normal即正态分布，并设置均值为0；第二种是random_uniform即随机初始化，并设置最小值为0。表6为4组参数组合，图5是对模型收敛速度的影响，图6是对模型正确率的影响。从结果可以看出随机初始化收敛速度相对较快一些，但是正确率总体相对较低。

Tabel 6 Parameter choice表6 参数选择

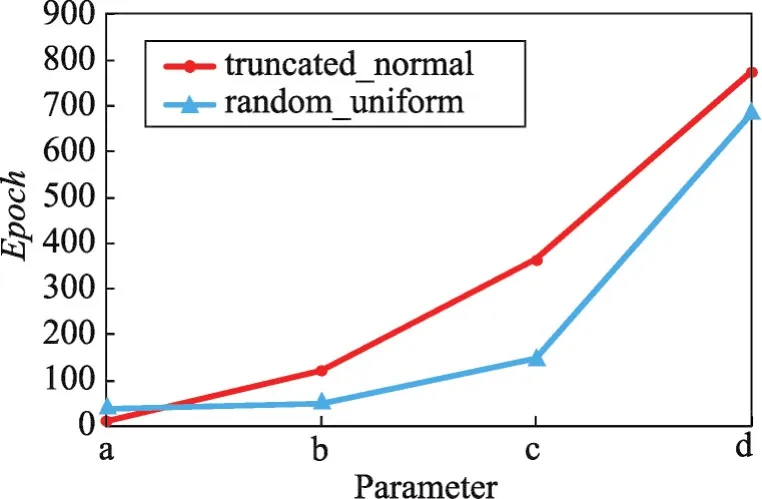
Fig.5 Influence of weight initialization method on convergence speed图5 权重初始化方法对收敛速度的影响

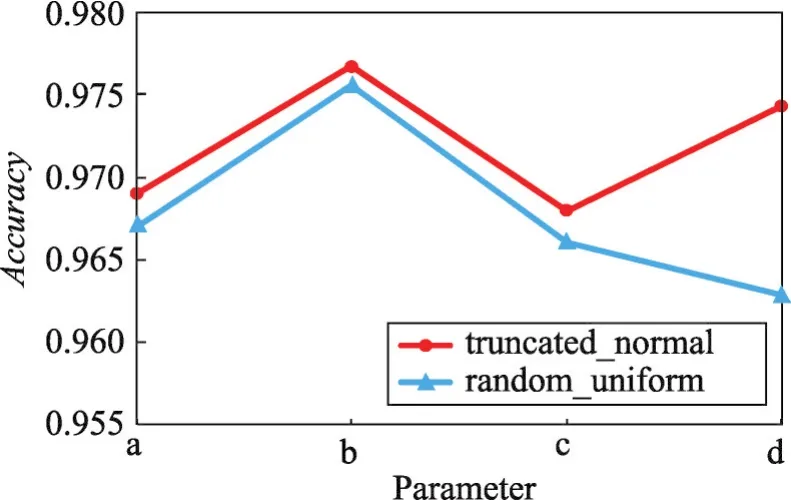
Fig.6 Influence of weight initialization method on accuracy图6 权重初始化方法对正确率的影响

5 总结与展望

本文提出了基于深度学习的网络邻居结构影响力模型DNSI，它可以通过自动提取特征得到三种邻居结构的影响力，并根据这三种影响力进行节点属性预测、类别中心度度量和用户行为预测。通过在多个真实网络数据集上进行的实验，证明了DNSI在不同的应用场景下都可以有优秀的表现。并且发现普遍情况下，加强二度邻居结构的影响力最高，也间接说明网络中节点联系越紧密，交互行为越频繁，对目标节点的影响就越大。

下一步，将从以下几方面继续尝试：

（1）除本文三种邻居结构外，继续拓展邻居节点的度数，比如三度、四度邻居结构等。

（2）除CNN深度学习方法外，尝试结合其他深度学习算法，得到更为精确的邻居结构影响力。

（3）更好地利用不同的邻居结构影响力。本文已经证明通过不同邻居结构影响力可以进行节点属性预测、类别中心度度量和用户行为预测，在其他的方面可能也会有较大的潜力，可以继续进行应用研究。