一种基于元胞自动机的人群疏散仿真算法研究
2019-02-11吴凡李春忠林丽芳朱家明
吴凡, 李春忠*, 林丽芳, 朱家明
( 1.安徽财经大学 统计与应用数学学院; 2.安徽财经大学 会计学院: 安徽 蚌埠 233000 )
人群疏散仿真模型可通过离散式、动画式的图像模拟人群疏散时的情形,因此该模型可为相关管理者制定科学有效的疏散方案提供依据.目前,仿真疏散模型主要分为宏观模型与微观模型.宏观模型最早由Henderson提出[1],该模型将行人活动看作是气体或流体,但因行人活动不能像气体或流体一样完全遵循能量守恒等物理规律,因此该模型过于理想化.微观模型主要是以个体、周围个体、周围环境为切入点,对三者间的交互影响进行研究.该模型可以较为理想地表现出个体特性与群体活动,仿真结果更加切合实际.在微观模型中,应用较为普遍的是社会力模型,该模型通过研究影响人群疏散时的挤压、恐慌等物理或心理因素,以复杂的社会力刻画个体间的直接信息传递,进而可较好地重现集体行为与自组织现象[2].2014年,孙凯[3]在微观社会力模型的基础上,根据学生疏散时的社会行为特征设定了相应的疏散规则,但该研究只考虑了单楼梯、单一地形的人群疏散仿真模型,因此所得结论缺少实用性.2017年,李之红[4]基于行为决策机理建立了人群密集场所行人个体逃生行为的模型构架,并探讨了人群拥挤场所中个体社会力对群体社会力的影响.但目前为止,相关文献对多层复杂地形疏散的研究较少;为此,本文以安徽博物院为例,结合元胞自动机与最小费用最大流的思想设计算法,将行人状态、疏散地形、行人行为特征分开运算,提出一种针对多楼层、复杂地形的人群疏散规则,并在Matlab r2016b环境中,分别对博物院单层、多层参观者的疏散行为进行仿真,以此为相关部门制定科学的疏散方案提供依据.
1 人群疏散仿真模型与算法
1.1 元胞状态值的设定
首先对安徽博物院平面地图进行灰度处理,之后将每个像素点视为元胞,地图墙壁等无法到达的障碍物(图1中的黑色部分)设定为0, 参观者设定为1, 空地设定为2, 第i个出口(图1中的虚线部分)的元胞值设定为Ui(Ui为充分大的整数,i=1,2,…,n).按上述方法所制得的安徽博物院地形示意图如图1所示.
1.2 元胞属性的设定
为建立元胞的属性矩阵,本文从地形、心理等方面对影响行人疏散的因素进行研究,各量化因素为:
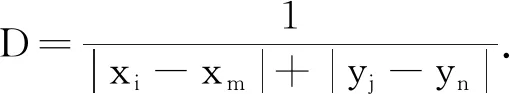
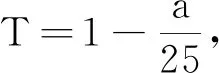

图1 安徽博物院地形示意图

图2 拥堵值示意图
3)从众值.从众值C表示当发生突发事件时,参观者因对环境、地形等不熟,或者因遭到惊吓丧失理性判断而采取紧随大多数人逃离现场的行为.当参观者抵达某一元胞,元胞的从众属性值会增加;而当参观者离开某一元胞时,元胞的从众属性值会衰减.计算从众值的具体流程如下:
a)初始时,将所有元胞的从众属性设定为0, 即Ct0=0.
b)当有人抵达元胞时,从众值加1, 即ΔC=1.
c)当有人离开元胞时,从众值以0.5的倍率衰减.
考虑到参观者对博物院的熟悉程度与自身的心理素质对其从众心理的影响,引入Ki⊆[1,10]与Li⊆[1,10]对参观者的心理进行量化,并按正态分布的方式为每个参观者进行赋值.在所赋的值中, 1表示最不熟悉或最惊慌, 10表示最熟悉或最理智.由上述得从众值的计算表达式为
(1)
4) 指引值.指引值O表示工作人员对人群疏散行为所产生的影响.当有工作人员进行疏散时,可将绝大多数参观者看作是完全从众心理,即将Ki与Li均取值为1;而当没有工作人员引导时,该项指标不对疏散产生影响.指引值的计算表达式为
(2)

5) 逃离值.逃离值efd表示当前时刻当前位置逃离时的难易程度,逃离值越大逃离就相对越容易.逃离时,参观者会自发的从逃离值小的地方向逃离值大的地方前进,直至逃离.逃离值的表达式可表示为
efd=D+T+C+O.
(3)
1.3 元胞自动机人群疏散算法

一层建筑的元胞自动机的运行规则是按出口编号从小到大进行遍历,仿真开始时,若:
1)元胞状态值s=1, 且周围元胞不存在状态值s=2或者s=Ui; 或者元胞状态值s=2, 且周围元胞不存在状态值s=1: 则下一时刻元胞值不发生变化.
2)元胞状态值s=1, 且周围元胞存在状态值s=2; 或者元胞状态值s=2, 且周围元胞状态值存在s=1: 则通过式(4)和(5)计算下一时刻的元胞值.
3)元胞状态值s=1, 且周围元胞存在状态值s=Ui, 则下一时刻元胞状态值s=2.
为建立状态值演变方程,首先建立选取最优逃离值的辅助函数:
令
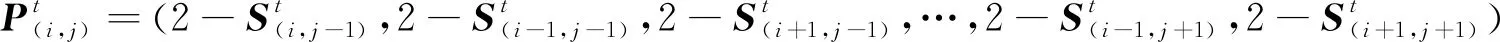
根据最小费用最大流的思想,将属性矩阵EFD视为容量,将状态矩阵S视为流量[6],则有
(4)
(5)
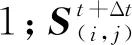
多层建筑的元胞自动机的运行规则是将上下连通的出口设为相同状态值,并将每个数值矩阵的宽度设定为k3, 然后将多层平面地图数值化后合并至同一矩阵,按出口编号从小到大进行遍历.仿真开始时,若:
1)元胞状态值s=1, 且周围元胞不存在状态值s=2或者s=U(m,n)时;或元胞状态值s=2, 且周围元胞不存在状态值s=1时:则下一时刻元胞值不发生变化.
2)元胞状态值s=1, 且周围元胞存在状态值s=2时;或元胞状态值s=2, 且周围元胞存在状态值s=1时:则通过式(4)和(5)计算下一时刻的元胞值.

2 仿真结果与分析
2.1 基于单层的人群疏散仿真结果分析
首先利用Matlab r2016b对安徽博物院第3层展厅内人群疏散的状况进行仿真,并分别截取0、 154、 1 045、 1 337 s时刻的疏散状态,如图3所示.由图3可看出,当t=1 337 s时,疏散完成.这表明,本文算法可以完整实现单层的疏散仿真过程.

图3 不同时刻时的单层疏散状态示意图
2.2 基于多层的人群疏散仿真结果分析
利用Matlab r2016b对博物院1至4层展厅内人群疏散的状况进行仿真,并截取仿真初始时刻与拥堵时刻的疏散状态,如图4和图5所示.由图4可以看出,在未发生事故时,人群随机分布在场馆的各处.由图5可以看出,事故发生后,随着时间的不断推移,人数最多的一层出现明显的队列现象,这表明人数较多时人群的从众心理对疏散行为会产生较大的影响;而在人数最少的4层,人群呈现的是不规则的逃离现象.上述现象与实际较为相符,表明本文算法可以完整实现多层疏散的仿真过程.

图4 疏散初始时14层的状态示意图

图5 疏散拥堵时14层的状态示意图
2.3 基于疏散时间的仿真结果分析
为进一步了解仿真过程中各楼层所剩余的人数,绘制各楼层剩余人数与疏散时间以及总剩余人数与疏散时间的关系图,如图6所示.因本文将1、2层人数的初始值设定为相同,因此若1、2层具有相同的疏散性能,则1层楼内因疏散而减少的人数应能抵消2层楼内疏散而涌入到1层的人数.但由图6可以看出,当t∈(0,178)时, 1层的人数不断增加,这说明1层的疏散性能低于2层,因此1层的疏散结构需进一步优化.
将赋予指令值条件下的每一层疏散仿真调度时间与没有赋予指令值条件下的疏散仿真调度时间进行对比,得如图7所示的条形图.由图7可以看出,当每一层都有工作人员进行疏散时,疏散时间由原来的4 423 s降至为1 876 s,即降低至原来时间的42.41%.

图6 馆内总人数和各楼层剩余人数与时间的关系图
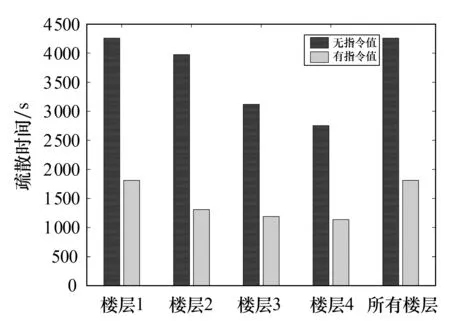
图7 有无指令值的疏散时间对比图

图8 3种算法在不同人流密度下的人群疏散时间
3 不同算法的仿真结果对比
本文利用文献[7]中的数据和地形对传统算法[7](将人群中的个体视为简单粒子的一类算法)、文献[7]算法和本文算法进行仿真,结果如图8所示.从图8可以看出:本文算法和文献[7]算法的仿真结果均明显优于传统算法;人流密度较小时,本文算法的疏散时间略低于文献[7]算法的疏散时间,但随着人流密度的增加,本文算法的疏散时间略高于文献[7]算法的疏散时间.随着人流密度的增加,本文算法的疏散时间略高于文献[7]的原因是文献[7]中没有考虑到人群中个体的恐慌等负面情绪,且人流密度越大这些因素对疏散时间的影响越明显.但综合来看,本文算法与文献[7]算法的仿真结果较为接近.
4 结论
本文将最小费用最大流的思想与元胞自动机相结合,构建了安徽博物院人群疏散仿真模型.仿真结果显示,博物院1层的疏散性能低于2层,工作人员的疏散引导有利于降低疏散时间(降低至原来时间的42.41%).本文算法和文献[7]算法的仿真结果均优于传统算法,在人流密度较大时本文算法的仿真结果虽然略高于文献[7]模型,但因其考虑了人群中个体的恐慌等负面情绪,因此本文模型更符合实际.本文结果可为高层建筑的应急工作提供参考.本文在定义元胞属性的逃离值时,由于缺乏实际疏散数据未能考虑到各因素的权重大小,而是直接将各因素进行加总;因此,在今后的研究中,我们将结合真实的疏散数据,并利用神经网络等学习方法训练出最佳的权重系数,进而优化本文算法.
