气井临界携液流量计算方法的修正

薛军 张茂林 宋惠馨 王贺 张艺钟 彭军 唐雯

摘      要：氣井最小临界携液流量的准确计算对于确定气井合理配产、优化气田开发方案具有非常重要的意义。国内外学者在Turner模型的基础上，对临界携液系数进行修正，从而推导出了不同的临界携液流量计算模型，但这些模型均将界面张力和天然气偏差因子取为常数，忽略了温度和压力对它们的影响。因此，对液滴模型进行了修正，通过经验公式计算界面张力，运用DAK方法计算天然气偏差因子，提出了考虑实际界面张力和天然气偏差因子的气井临界携液流量模型。应用修正前后的3种常规模型分别对某气田的临界携液流量进行计算对比，结果表明修正的临界携液模型能够更加准确预测气井状态，判断井筒是否积液，较常规模型具有更高的准确性和科学性，适用于气田实际生产开发。

关  键  词：临界携液流量;界面张力;天然气偏差因子

中图分类号：TE122        文献标识码： A       文章编号： 1671-0460（2019）11-2614-04

Correction of Calculation Method of Critical Fluid Carrying Flow in Gas Well

XUE Jun¹， ZHANG Mao-lin²， SONG Hui-xin¹， WANG He¹，

ZHANG Yi-zhong²， PENG Jun³， TANG Wen⁴

（1. School of Petroleum Engineering， Yangtze university， Hubei Wuhan 430100， China;

2. Collaborative Innovation Center for Unconventional Oil and Gas， Yangtze University， Hubei Wuhan 430100， China;

3. Jianghan Oilfield Branch Exploration and Development Research Institute， Hubei Wuhan 430073， China;

4. Southwest Oil and Gas Field Chongqing Gas Field， Chongqing 400021， China）

Abstract：  The accurate calculation of the minimum critical fluid carrying flow of gas wells is of great significance for the determination of reasonable gas well production allocation and optimization of gas field development program. On the basis of Tuner model， scholars at home and abroad modified the critical fluid carrying coefficient， thus different critical fluid carrying flow calculation models were derived. However， these models take the interfacial tension and natural gas deviation factors as constants and ignore the influence of temperature and pressure on them. In this paper， the droplet model was modified， the interfacial tension was calculated by empirical formula， the deviation factor of natural gas was also calculated by DAK method，and the gas well critical fluid carrying flow model considering the actual interfacial tension and the deviation factor of natural gas was proposed. The critical flow rate of a gas field was calculated by three general models before and after modification. The results showed that the modified critical fluid transport model was more accurate than the conventional model in predicting gas well status and determining whether there was fluid accumulation. So it is applicable to the actual production and development of gas field.

Key words： critical fluid carrying rate; interfacial tension; deviation factor of natural gas

气井最小携液临界流量的精确计算对于气田开发方案编制具有十分重要的意义^[1]。在有水气藏开发中后期，气藏压力逐步降低、气井产水量逐渐增大，出水导致井筒内压力损耗增加，达到同样的产量需要更高的携液举升井底压力，或同样的井底压力只能获得较低的井口产量^[2]，使得气流难以携带井底产出水到达地面，从而在井底形成积液^[3]。气井积液会增大井底回压，导致气井产量下降，严重时甚至会将气井压死，从而造成停产^[4-7]。为了避免产生积液，气井产量必须大于临界携液产量，通过运用临界携液理论计算临界携液产量（最低产量），以此评价出水气井的合理产量范围，确定气井的合理配产^[8，9]。

1996年Turner^[10]通过对垂直管流中液相的流动方式的研究，提出了球形液滴模型来预测积液的形成，并推导出了临界携液流量计算公式。之后许多学者^[11-14]在液滴模型基础上分别在模型系数、液相流动方式、液滴形状等方面作了大量工作。2001年李闵^[15]认为液滴在高速气流中运动时由于压差作用会变形成椭球体，由此推导出气井连续排液临界携液模型。2007年王毅忠^[16]根据高速气流中运动的球帽形液滴，认为模型中液滴应为球帽状，由此推导出气井最小携液临界流量计算公式。但是液滴模型中气水界面张力通常被认为是常数60 mN/m，而实验表明其数值随压力与温度的变化而变化^[17，18];天然气偏差因子Z通常取常数0.88，但其数值明显受到温度和压力的影响^[19]。因此，在求解气井临界携液流量时，有必要考虑实际气水界面张力和天然气偏差因子的影响。

1  气井临界携液流量计算公式的修正

液滴模型主要有Turner 模型^[10]、李闵模型^[15]、和王毅忠模型^[16]，各模型的携液临界流速不同，见表1。

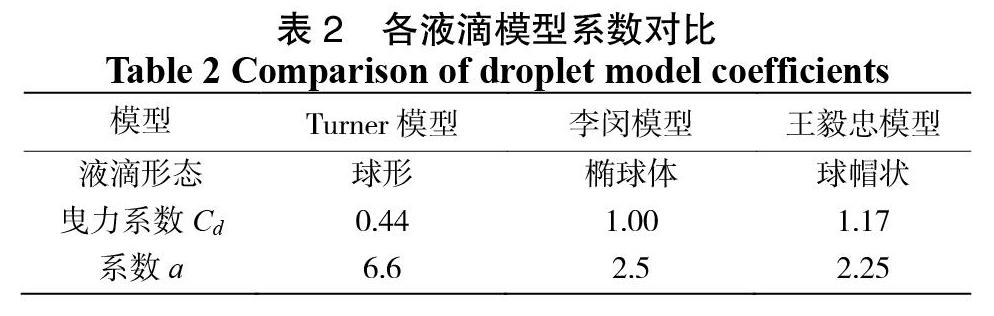
3种液滴模型中，假设条件分别为球形、椭球形和球帽形3种状态的液滴，曳力系数C_d是流体作用于颗粒上的曳力对颗粒在其运动方向上的投影面积与流体动压力乘积的比值^[20]，与液滴形态有关，故不同状态的液滴相對应取不同的曳力系数C_d^[16]。Turner模型中球形液滴曳力系数取为0.44，李闵模型中椭球形取为1.0，王毅忠模型中球帽形液滴根据实验数据将曳力系数取为1.17，将对应的C_d代入各模型临界流速公式，得到各模型的模型系数a，见表2。

各模型的携液临界流速均可用下公式^[21]表示：

     （1）

（2）

（3）

式中：ν_g-携液临界流速，m/s;

q_c-携液临界流量，10⁴m³/d;

ρ_g-天然气密度，kg/m³;

ρ_l-地层水密度，kg/m³;

σ-气水界面张力，N/m;

a-模型方程系数;

γ_g-天然气相对密度;

p_wf-井底流压，MPa;

T-井底温度，K;

Z-天然气偏差因子;

A-油管截面积，m²;

D-油管直径，m（注：也可用井口压力、井口温度、及井

口压力温度下的Z）。

气水表面张力可由以下经验公式^[22-24]进行计算：

     （4）

s₁ =76exp（-0.036 257 5p）;s₂ =52.5-0.870 18p）  （5）

式中：σ-溫度为t℃时水的表面张力，mN/m;

σ₁-温度为23.33 ℃时水的表面张力，mN/m;

σ₂-温度为137.78 ℃时水的表面张力，mN/m;

t-某一时刻水的温度，℃;

p-某一时刻压力值，MPa。

1975年Dranchuk和Abou-Kassem在Starling和Carnahan修正的BWR状态方程基础上，对1500个原始Standing-Katz偏差因子数据进行非线性回归分析，提出了11个常系数的SC-BWR状态方程计算天然气偏差因子的DAK方法^[25，26]。其表达式为：

（6）

     （7）

（8）

（9）

（10）

式中：ρ_r—天然气拟对比密度;

T_r—天然气拟对比温度;

p_r—拟对比压力;

Z—天然气偏差因子;

a₁-a₁₁—系数（在DAK模型中各值分别为：a₁=0.326 5，

a₂=-1.070 0，a₃=-0.533 9，a₄=0.015 69，a₅=-0.051 65，

a₆=0.547 5，a₇=-0.736 1，a₈=0.184 4，a₉=0.105 6，

a₁₀=0.613 4，a₁₁=0.721 0）。

该方法为非线性隐式方程，使用牛顿-拉弗森迭代法求解。

将代入式（1），将代入式（2）、式（3），则得到考虑实际气水界面张力和天然气偏差因子的气井临界携液流量公式。

       （11）

                （12）

（13）

修正后的公式將、考虑在内，可以在一定程度上提高气井临界携液流量计算结果的准确性。

2  实例计算分析

表3基础数据来自某气田，天然气相对密度0.584 5，临界压力4.68 MPa，临界温度193.6 K;气水界面张力由实测温度压力数据计算所得，地层水密度为1 000 kg/m³。

由表3可以看出，对于气井，是否考虑实际界面张力和天然气偏差因子对于临界携液流量计算结果影响较大。利用Turner模型计算该气田的临界携液流量存在的误差较大，在判断气井是否积液时与实际结果偏差较大，修正后的Turner模型在一定程度上减小了误差;利用李闵模型计算该气田的临界携液流量，存在气井实际产量在低于李闵模型计算的临界携液流量时，气井仍然可以正常生产，未出现积液的现象，修正后的李闵模型计算的临界携液流量与实际生产资料更加符合;利用王毅忠模型计算该气田的临界携液流量结果误差较小，均可以较准确地预测气井状态，但是修正后的王毅忠模型进一步提高了计算结果的准确性和可靠性，与实际情况更加吻合。

将实际气井产量与各公式计算的最小携液产量进行比较。若实际产气量等于最小携液产量，数据点就会落在图中的对角线上。如果公式适用，那么，接近积液气井的数据应该接近这条对角线，未积液气井的数据应在这条对角线的上面，而积液气井的数据落在对角线的下面。由图1可以看出，修正后的Turner模型计算结果偏大，不能准确预测气井积液状态;修正后的李闵模型和王毅忠模型计算结果跟生产实际值较为吻合，可以较准确预测气井积液状态^[27，28]。

由此可见，根据实际生产资料，修正前后的Turner模型均不适用于该气田;修正前后的李闵模型虽然在判断气井是否积液时结论比较一致，但由计算结果可以看出，修正后的李闵模型更加符合实际;修正前后的王毅忠模型计算结果均适用于该气田，但修正后的王毅忠模型准确性和可靠性更高。

对于气田，单井合理配产也是一个重要的开发指标，尤其是对于出水气井，在实际生产中合理配产的确定需充分考虑气井最小临界携液流量，避免由于配产过低造成井筒积液，对气层造成损害，产生不可估量的经济损失。因此，在确定合理配产时，应该综合分析修正前后模型的临界携液流量结果，避免气井水淹，以保证气田正常、有序开发。

3  结论

（1）在结合生产实践的基础上，对计算临界携液流量的常用模型：Turner模型、李闵模型和王毅忠模型在理论上进行了修正，提出了考虑实际界面张力和天然气偏差因子的临界携液流量计算公式。

（2）根据某气田实际生产资料分析，是否考虑实际界面張力和天然气偏差因子对临界携液流量的计算结果有较大影响。考虑实际界面张力和天然气偏差因子的李闵模型和王毅忠模型计算结果与气井实际生产资料更加吻合，具有更高的准确性、可靠性和科学性，可作为气井积液的判断标准。

（3）对于气井，尤其是出水气井，应当采用多种模型相结合以及修正前后模型相结合的方法，以此分析气井携液能力，进行合理配产。

参考文献：

[1]李元生， 滕赛男，杨志兴，等. 考虑界面张力和液滴变形影响的携液临界流量模型 [J] . 石油钻采工艺，2017， 39 （2）：218-223.

[2]秦涛， 柴小颖， 毛凤华， 谢梅， 李兴彦. 涩北一号气田井筒积液诊断模式及判断[J]. 青海石油， 2012， 30 （02）： 51-55.

[3]魏纳，李颖川，李悦钦，等. 气井积液可视化实验[J]. 钻采工艺，2007，30 （3）：43-45.

[4]刘双全，吴晓东，吴革生，等. 气井井筒携液临界流速和流量的动态分布研究[J]. 天然气工业，2007， 27 （2）：104-106.

[5]谭晓华，李晓平. 考虑气体连续携液及液滴直径影响的气井新模型[J] . 水动力学研究与进展，2013， 28 （1）：41-47.

[6]杨蕾， 刘宁， 刘辉， 王华军. 气井井筒携液模型研究与应用[J]. 天然气与石油， 2011， 29 （02）： 48-49+61+2.

[7]李品， 江厚顺， 王萌， 隋海庆， 吴岸. 气井井筒积液预测模型优选[J]. 当代化工， 2016， 45 （08）： 1820-1823.

[8]罗睿.  JHS低渗透气藏气藏工程研究[D]. 西南石油大学， 2014.

[9]潘杰， 王武杰， 魏耀奇， 陈军斌， 王亮亮. 考虑液滴形状影响的气井临界携液流速计算模型[J]. 天然气工业， 2018， 38 （01）： 67-73.

[10]TURNER R G，HUBBARD M G，DUKLER A E.Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells[J]. Journal of Petroleum Technology， 1969， 21（11）： 1475-1482.

[11]COLEMAN S B， CLAY H B， MCCURDY D G， LILI L N.A new look at predicting gas-well load-up[J]. Journalof Petroleum Technology， 1991， 43（3）： 329-333.

[12]Nosseir，M.A. A New Approach for AccuratePrediction of Loading in Gas Well Under Different FlowingConditions[C].SPE 37408，1997.

[13]彭朝阳. 气井携液临界流量研究[J]. 新疆石油地质，2010，31（1）：72-74.

[14]熊健，李凌峰，张涛. 气井携液临界流量的计算方法[J]. 天然气与石油，2011，29（4）：54-56.

[15]李闽，郭平，谭天光. 气井携液新观点[J]. 石油勘探与开发，2001， 28（5）：105-106.

[16]王毅忠，刘庆文. 计算气井最小携液临界流量的新方法[J]. 大庆石油地质与开发，2007， 26（6）：82-85.

[17]SUTTON R P. An improved model for water-hydrocarbon surface tension at reservoir conditions[R]. SPE 124968， 2009.

[18]刘刚. 气井携液临界流量计算新方法[J]. 断块油气田，2014， 21（3）：339-343.

[19]郭布民，敬季昀，王杏尊. 气井临界携液流量计算方法的改进[J]. 断块油气田，2018，25（4）：484-487.

[20]郑思佳. 气固两相流中采气管线关键易损件冲蚀特性研究[D].西南石油大学， 2016.

[21]纪成. N气藏动态分析及产能研究[D]. 西南石油大学， 2015.

[22]杨继盛.采气工艺基础[M].北京：石油工业出版社，1994：330-334.

[23]陈元千. 油气藏工程实用方法[M]. 北京： 石油工业出版社，1990：442-452.

[24]杨继盛，刘建仪.采气实用计算[M].北京：石油工业出版社，2004：42-46.

[25]Dranchuk P M，Abou-Kassem J H.Calculations of z factors for natural gases using equations of state[J].Journal Canadian Petroleum， 1975， 14 （3）： 34-36.

[26]胡建國，郭分乔，许进进. 计算天然气偏差因子的DAK方法的修正[J]. 石油与天然气地质，2013， 34（1）：120-123.

[27]郑军， 闫长辉， 张文洪， 郑峰， 徐卫峰. 大牛地气田气井最小携液产量研究[J]. 油气地质与采收率， 2011， 18 （01）： 70-73+116.

[28]李闽， 郭平， 张茂林， 梅海燕， 刘武， 李士伦. 气井连续携液模型比较研究[J]. 西南石油学院学报， 2002 （04）： 30-32+3.