挖掘习题潜在功能,开发习题隐性价值
2019-02-03卢国清
卢国清
摘 要 习题是小学数学教材的重要组成部分,是不可或缺的课程资源,是学生开展数学学习的主要载体。数学习题的价值主要體现在两个方面:学生通过练习巩固所学基础知识,形成基本技能,培养数学思考和解决问题的能力,这是习题的显性价值;通过练习让学生受到基本数学思想方法的熏陶,这是习题的隐性价值。然而,在我们的日常教学中,普遍存在着这样的情况:教师在重视例题的教学的同时,却忽略了对课本习题的深入研究,练习只是平铺直叙、就题讲题,致使许多习题隐含着的价值未能得到开发利用,潜在的功能没能被挖掘,从而练习效果大打折扣。
关键词 小学数学 习题潜在功能
中图分类号:G633.7文献标识码:A
本文我就自己对一道课本中的练习题的教学过程,谈谈教师应该怎样充分挖掘课本习题的练习功能,提高练习的实效。
苏教版数学12册81页【第9题】:用同一张长方形纸可以卷成两个大小不同的圆柱。选一张长方形纸,用不同的方法卷一卷,分别算出体积。
这一题,如果就题论题开展教学,教师出示一张给出长、宽数据的长方形纸,让学生算出围成圆柱的体积,学生得到的仅仅是再次进行了一次圆柱体积计算的练习而已。
我在教学中是这样做的:
第一层次:我让学生拿出一张准备好的长方形纸,提出问题“把这张长方形纸围成圆柱,有几种围法?”学生小组合作,拿出准备好的纸进行操作,很快说出了有两种不同的方法。接着老师追问:“围成的两个圆柱,有什么不同?”,让同桌的两个{或前后四个}学生,拿着围成的不同圆柱一起进行比较。通过比较,使学生进一步明确了:第一种围法长方形纸(侧面)的长是圆柱的底面周长,宽是圆柱的高;第二种围法则相反。通过对“有几种围法”的讨论,培养了学生的发散性思维;通过对围成的两个圆柱不同点的比较,突破了平时练习中“已知圆柱侧面的长和宽,求圆柱体积”这一难点。
第二层次:老师提问“你能估计一下两个圆柱哪个体积比较大吗”。这时,学生有的看着围成的圆柱体,凭着直观感觉判断大小;有思维灵活的同学想到把细长的那个圆柱插进粗矮的那个圆柱,再设想把露在外面的那段截下后再插进粗矮的那个,看看能不能占满它的空间;还有几个逻辑思维较强的学生,则根据两个圆柱底面周长和高之间的关系进行分析和推理得出了结论。学生判断有对有错,激烈的争辩,点燃了学生思维的火花,在判断过程中,通过数和形的完美结合,学生的直觉形象思维和抽象逻辑思维能力得到了提高。学生的智慧由内而外,自由流淌在他们各自独特的见解中。
第三层次:在同学们谁大谁小的争论声中,老师提议学生一起用数据计算出他们体积,来验证谁的判断正确。老师举起手中的长方形纸,问:“要计算这张长方形纸围成的两个圆柱的体积,应该知道那些数据?你能给出两个数据,使计算尽量简便些吗?”学生很快说出要给出长和宽的数据,但是给出的什么样的数据能使计算简便,产生了不同的想法。开始绝大部分同学给出的数据都是长20厘米、宽10厘米之类的整数或整十数,老师不失时机地说“请你再想想,用这些数据计算容易吗?为什么?”在老师的追问声中,学生在头脑中完成了这样一个思考过程:长方形纸的一条边的长度就是围成圆柱的底面周长,而要计算圆柱的体积先要求出底面半径,所以只有长和宽的数据都是圆周率的倍数时才便于求出底面半径。学生在这一考虑数据的思考过程中,头脑中完成了一个公式化的圆柱体积演算过程,一方面巩固了计算圆柱体积的列式计算方法,另一方面发展了抽象思维能力。
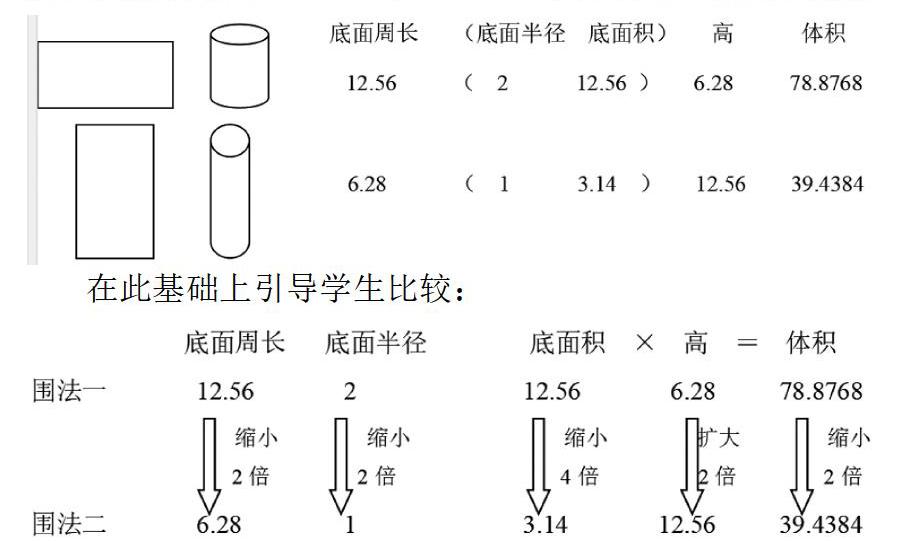
第四层次:为了便于计算后进行比较,老师给定长方形纸的长和宽分别是12.56cm和6.28cm.,让全体学生按给出的数
在此基础上引导学生比较:
进而得出规律:长方形纸的长是宽的n倍,围法一的底面周长是围法二的n倍,所以底面积扩大了n2,而高缩小了n倍,所以体积扩大了n倍。为学生以后一个解答这类数学问题建立了起了一个数学模型。
一道习题,发挥的功效不亚于八道、十道一般的练习题。四个层次,环环紧扣,步步深入,既有判断推理,又有分析解答,既巩固了基础知识、训练了基本技能,又培养和发展了学生的观察比较、分析推理以及抽象思维等多种能力,同时还让学生受到了假设、数形结合、数学模型等数学思想方法的熏陶。
总之,在全面推进课程改革的今天,教师在数学课堂教学中,认真钻研教材,领会教材编写意图,善于发掘教材潜能,开发课本练习题的隐性价值,对提高课堂教学效率和数学教学有效性具有十分重要的意义。充分发挥课本习题的功能,用足用好每一道习题,一题多练、一题多用,既能减轻老师课前准备的负担,更有利于切实减轻学生的课业负担,做到真正的减负增效。
