基于大样本数据对比分析数学分层教学效果

李春林

[摘           要]  高等数学作为高职院校课程中极为关键的一门基础课程，已成为高职生学习的难点课程，而且现在高职生在数学基础知识和学习习惯上也存在着很大的差异性，很多高职院校实施了分层教学。以江苏常州工程职业技术学院近两年实施数学分层教学后收集到的学生测试成绩为大样本数据基础，建立多水平线性模型，用SPSS19.0软件统计分析比对数学分层后的测试成绩做显著性检验，从而阐述学生数学分层实现了因材施教的目的。

[关    键   词]  分层教学;大样本数据;多水平线性模型;显著性检验

[中图分类号]  G712                   [文献标志码]  A                      [文章編号]  2096-0603（2019）36-0052-02

一、背景

随着教育体制的不断改革和扩张，以及社会对人才的需求层次发生了变化，近几年国家大力发展职业教育，与此同时对课改也提出了新的挑战。探索一种适应职业院校学生特点的教学方法成为各职业院校教育工作者的当务之急，而分层教学由于其特殊性，在很多职业院校已经开展，分层教学对不同层次的学生的影响是存在的。随着信息技术的发展，大样本数据已经成为热门的研究对象。现代高等职业教育分层教学中所产生的大样本数据涉及学生、教师、学校、企业等多个领域。本文采集了我院两千多名学生的入学时分层测试成绩与分层后的两次期末测试成绩为样本数据，建立多层次线性模型，从固定效应和随机效应分析分层教学的优势。

二、模型原理与方法

多层线性模型是一种处理嵌套数据的统计方法。通过定义不同层的模型，将随机变异分解为两个部分，一个是第一水平个体间差异带来的误差，另一个是第二水平的差异带来的误差。可以假设第一水平个体间的测量误差相互独立，第二水平带来的误差在不同水平之间相互独立。多水平分析法同时考虑到不同水平的变异，下面结合本文要阐述的问题，建立两水平数学模型。

水平1的模型，描述学生个体入学测试成绩对后续测试成绩影响的线性模型;

Y_ij=β_0j+β_1jx_ij+ε_ij

Y_ij表示第i个学生的第j个层次（专业或班级）的两次期末测试成绩与入学测试成绩的差异值的平均值（简称pcstg）。这里的截距β_0j和斜率β_1j用来描述不同的学生有不同的截距和斜率，x_ij表示观察值i在单位j中的入学测试成绩。

水平2模型，描述个体间的差异对学生个体间发展的差异进行解释，就关心的学生嵌套的受教层次、专业、行政班级等因素对成绩的影响进行分析和解释。

β_0j=γ₀₀+γ₀₁w_j+u_0j

β_1j=γ₁₀+γ₁₁w_j+u_1j

合并模型：

Y_ij=γ₀₀+γ₀₁w_j+u_0j+γ₁₀x_ij+γ₁₁w_jx_ij+u_1jx_ij+ε_ij

其中：wj表示第二水平（如层次、专业、班级）的预测变量，γ00和γ10分别表示截距和斜率的整体均值，用来描述总体的变化趋势。随机部分u0i和u1i表示截距和斜率的残差。

三、模型分析

（一）样本数据与研究问题说明

从本校抽取数据完整的学生2278名学生，其中A层次1030名，B层次1248名，记录了入学测试成绩与两学期的期末测试成绩。这些学生数据嵌套在学校的2个层次，7个专业，72个行政班级，20个教学班级中。

研究的问题：通过这三次测试成绩，追踪分析每个学生在入学分层后，个人成绩的发展趋势特点，即增长（或下降），不同的学生在这一时期的数学成绩发展是否存在个体之间的差异，如果存在差异，能否用一些变量来解释或预测这些差异。

（二）入学后学生个体成绩提高情况分析

本数据集采集了2278名学生的数据资料，各个层次、专业、行政班级、教学班级的入学平均成绩和提高的平均成绩各不相同，为了统一和全面分析学生入学后数学成绩的变化情况，将以两个学期的测试成绩相对于入学成绩的差值的平均值（简称pcstg）作为本模型的因变量，打开SPSS的分析—描述统计—探索，以pcstg作为因变量列表，得直方图：

由图中数据看出，整体测试成绩平均提高了24.37，标准偏差为23.739，且正态分布，从而说明整个教学过程中，大部分学生的成绩都是提高的，接下来对比分析哪些因素与这个成绩的提高有关系。

（三）无条件模型——入学成绩对成绩提高的影响

首先检验入学测试成绩对个体成绩提高的影响，即第一水平模型的检验，打开SPSS 19.0，选择分析—混合模型—线性，将入学测试成绩cs1加入主题框，打开线性混合模型主对话框，将pcstg添加到因变量，不添加其他任何因子和协变量，打开随机效果对话框，勾选包括截距，协方差类型选方差成分，将主题cs1加入组合框，回到混合模型主对话框，确定得协方差参数估计表（见表1）：

根据表1数据分析，残差和截距[个体=cs1]方差的P<0.05，说明入学成绩cs1对pcstg的影响是显著的，那么在这个过程中，忽视了学生个体间的差异有对学生个体间发展的影响，所以接下来就关心的学生嵌套的受教层次、专业、行政班级等因素对pcstg的影响进行分析和解释。

（四）学生个体嵌套在各个层次、专业、班级对成绩提高影响的差异性比较

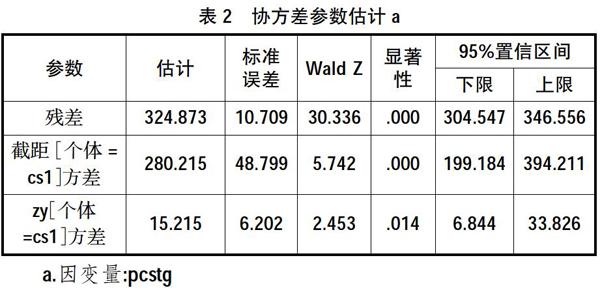
首先在上述模型中加入专业zy因子进行分析，打开SPSS 19.0线性混合模型对话框，依然选择cs1（入学测试成绩）为主体，保持pcstg为因变量，将专业zy添加到因子框中，打开固定效应对话框，将zy因子加入模型，打开随机效应对话框，将zy因子添加到随机模型，并勾选包括截距。回到线性混合模型对话框，确定运行，得协方差参数估计表（表2）如下：

观测和之前不加人任何因子相比有何变化，从这个检验得到的协方差参数估计表中，发现加入zy因子这个新变量是有统计学意义的，残差和方差的估计值明显有所减少，且截距[个体=cs1]方差的P<0.05，说明学生所在的不同专业对成绩的提高的影响是显著的。

第二步参照上述SPSS的设置过程，将模型中专业zy因子用班级jxbj因子替换进行分析，得到协方差参数估计表（表3）如下：

观测和之前的不加入任何因子与加人的专业zy因子相比有何变化，将表3与表1比较，发现加入jxbj因子这个新变量也是有统计学意义的，残差和方差的估计值同样明显有所减少，将表3与表2比较，发现在这个实验过程中，教学班级jxbj因子相对于专业zy因子对因变量的影响有点区别，残差与截距[个体=cs1]方差的估计值也在减少，但减少不多，而且jxbj[个体=cs1]与zy[个体=cs1]的方差估计值变化不大，截距[个体=cs1]方差都是P<0.05，从而说明这两个因子对学生成绩提高的影响都是显著的。

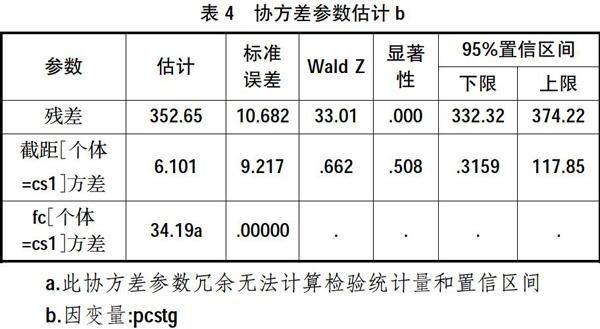
最后，同样参照上述步骤将模型中的因子用分层fc因子替换进行分析，得到协方差参数估计表（表4）如下：

观测表4和上述的表2，表3的变化，从表4中，发现加入分层fc因子这个新变量后，不仅让fc[个体=cs1]的协方差参数冗余，无法计算其检验统计量和置信区间，而且截距[個体=cs1]方差的标准误差大于估计值，显著性P=0.505>0.05，说明学生所在的层次对成绩的提高的影响是不显著的，从分层的角度来统计分析学生成绩的提高是没有意义的。

四、结论

综上所述，对于每个学生，入学成绩对成绩的提高有影响，应用多层模型分析发现，将学生嵌套到专业、班级后，专业和班级对学生成绩的提高的影响是显著的，但嵌套到层次中，从分层的角度对学生的成绩提高的影响反而不显著，这也正好说明，学生在不同的层次里，成绩的提高不会因为层次的不一样而受到影响，从而得出，学生入学时根据入学测试成绩的高低分层后，在不同层次上学，数学成绩的提高是一样的，因为教学方法和教学目标的修订，弥补了学生入学前的差异。

近年来我校在开展数学分层教学后，每次参加的江苏省普通高等学校高等数学竞赛和全国高职数学建模大赛，都取得了相对往年更好的成绩，从而也说明，开展数学分层教学，因材施教，根据不同基础的学生实施不同的教学方法，制定不同的教学目标，甄选不同的教学内容，不仅有效提高了全体学生的整体水平，也让基础好的学生发挥了自己的潜能，同时也照顾到了基础不好的学生。

参考文献：

[1]吴学品，刘殿国.多层统计模型的应用进展综述[J].统计与决策，2011（23）.

[2]李振，周东岱，董晓晓，等.我国教育大数据的研究现状、问题与对策：基于CNKI学术期刊的内容分析[J].现代远距离教育，2019（1）：46-55.

[3]吴希，张若东.基于SPSS的《高等数学》课程分层教学的探讨[J].数理医药学杂志，2010，23（1）：111-113.

[4]Aleksandra Klasnja Milicevic，Mirjana Ivanovi ，Zoran Budi-mac. Data science in education： Big data and learning analytics[J].Computer Applications in Engineering Education，2017，25（6）.

◎编辑 张 慧