卧式行星球磨机最佳衬板形式的数值模拟
2019-01-31朱飞
朱 飞
(1.合肥水泥研究设计院,安徽 合肥 230051)
(2.中建材(合肥)粉体科技装备有限公司,安徽 合肥 230051)
离散元法(discrete/distinct element method,DEM)是计算散体介质系统力学行为的数值方法,其原理源于较早的分子动力学(molecular dynamics),主要思想是把整个介质看作由一系列离散的独立运动的粒子单元所组成,具有一定的几何形状、排列方式和物理、化学特征;其运动受经典运动方程控制,整个介质的变形和演化由各单元的运动和相互位置来描述。离散元法最先由Cundall提出,王泳嘉最早引入我国,以后离散元法的研究及应用论文相继出现。
卧式行星式球磨机简称卧式行星磨,是一种新型的粉磨设备,离散元在行星磨的应用最早由Cundall和Strack在1979年利用DEM模拟技术模拟无机材料的粉磨效率,日本东北大学的Kano、Saito和 Mio等人对立式行星磨进行了DEM模拟研究。但迄今为止,对卧式行星磨的离散元模拟研究还没有涉及,本文用离散元法对卧式行星磨的粉磨介质的比冲击能进行模拟研究。
1 磨内钢球比冲击能的模拟
DEM模拟技术是计算机模拟钢球运动产生固体粒子运动行为的最流行最可靠的方法。可以计算出一个球与另一个球或磨壁碰撞的速度和相互作用力,准确地重现粉磨过程的钢球运动行为。笔者曾通过这个方法模拟了粉磨介质的三维运动,而模拟磨内钢球的比冲击能EW还是一种尝试。日本东北大学的研究证明,比冲击能和粉磨率成正比,钢球的比冲击能EW可以由两个相互碰撞的磨球或者一个球与磨筒内壁的相对冲击速度vi来计算,见式(1)。

式中:EW为钢球的比冲击能EW,J/s.g;m为单个钢球的质量,g;n为一个球撞击另外一个球或磨壁的次数,次/s;M为磨内装载的钢球总质量,g。
1.1 计算模型及参数选择
本文以颗粒流模型PFC3D 软件作为数值分析平台,利用fish语言编写程序进行二次开发和数值试验方案设计。模型中的筒体为一圆柱体,有效直径为89mm,深度为78mm。磨筒内沿周向均匀分布一定数量的长方形平面衬板,衬板宽度7mm,厚度和数量根据模拟数据可调。磨内钢球密度7.85g/cm3,设定为φ12mm、数量85个、总质量600g,在磨内呈自然分布。
卧式行星磨一般有3¯4个相同直径的筒体围绕主轴对称分布,故仅对其中一个磨筒进行模拟研究计算。磨筒公转速设定为300r/min,公转半径140mm,自转与公转反向旋转,转速可调。有关模型计算的具体参数见表1。
1.2 计算结果及分析
模拟计算中分别在有无衬板以及不同衬板厚度的情况下,改变自转/公转的转速比r,来探讨磨内钢球的比冲击能。
(1)衬板厚度对钢球的比冲击能的影响规律。
在无衬板时,钢球比冲击能EW随着转速比改变而变化的规律见图1。可以看出,随着转速比的增加,钢球的比冲击能是先增加后减小,在转速比r为4(自转转速1 200r/min)时,EW值最大,为0.127J/s.g;在转速比较小时,磨筒内钢球主要呈泻落状态,碰撞较弱,EW值较小。随着转速比的增加,钢球逐渐由泻落状态向抛落状态转变,同时钢球的比冲击能也在增加,越来越有利于粉磨,在转速比为4时EW达到最大值,此时钢球的抛落状态最佳,最适宜粉磨。转速比进一步增加,钢球向离心状态转变,碰撞突然变弱以至于几乎很少有碰撞的发生,所以比冲击能快速下降。
加装1mm衬板后,钢球的比冲击能EW随转速比r变化的规律见图2,可见随着转速比的增加,钢球的比冲击能也是先增加后减小,在转速比为3.5(自转转速1 050r/min)时,达到最大值为0.134J/s.g。与无衬板相比,比冲击能达到最大值时的自转转速略微变小,EW值仅略有增加,表明衬板厚度为1mm时,对钢球的运动影响不明显。

表1 行星磨离散元模型计算参数
分别将衬板厚度改为3mm、5mm和7mm时,钢球的比冲击能EW随着转速比变化的规律见图3。可见衬板厚度为3mm、转速比在1.5(自转转速450r/min)时,比冲击能EW值达到最大,为0.146J/s.g,而5mm和7mm的衬板,在转速比为1(自转转速300r/min)时,比冲击能EW达到最大,分别为0.125J/s.g、0.118J/s.g。

图1 无衬板时对EW的影响
由图1¯图3可以看出,钢球在无衬板条件下,比冲击能最大(即钢球碰撞最剧烈)时的转速比r为4,此时的自转转速为1 200r/min,这是因为钢球无衬板的提升作用而只是沿在磨壁滑动,不易被带起抛落,从而不易形成剧烈碰撞,这种状态的研磨能力非常有限;加装1mm厚度衬板后,比冲击能的最大值对应的转速比r减小不明显,EW值也只增加了0.007J/s.g,表明衬板太薄,不能显著起到阻止钢球滑动的作用;而采用3mm衬板后,转速比r为1.5即自转转速为450r/min时,钢球的比冲击能就达到最大,比无衬板的EW增值大0.019J/s.g,可以有效阻止钢球与磨筒的相对滑动,使得钢球形成抛落状态,加剧球与球或者球与筒壁的碰撞;当衬板厚度增大到5mm和7mm后,虽然比冲击能的最大值对应的转速比r减小到1,但是比冲击能EW也大幅度减小,因为钢球来不及抛落就被衬板带过而形成离心状态。因此,通过以上模拟,可以认为:卧式行星磨的衬板以3mm厚度比较合适,此时的比冲击能较大,钢球的抛落状态最佳,故而最适宜粉磨。在衬板规格、布置形式及数量相同的条件下,以衬板厚度3mm、转速比r分别为0.5、1.5和2.5时的钢球不同运动状态见图4。
图4中,r=0.5时钢球呈现泻落状态,r=1.5时钢球呈现抛落状态,r=2.5时钢球呈现离心状态。显然,行星磨的粉磨效率以3mm厚度衬板、转速比r=1.5为最佳。
(2)衬板数量对钢球比冲击能的影响。
采用不同数量衬板对钢球比冲击能EW的影响规律见图5。从图5可以看出,衬板数量分别为6、8、10块时,最大EW值对应的转速比r为1.5(自转转速450r/min),EW值分别为0.146、0.144和0.135J/s.g;衬板数量=2和4时,最大EW值对应的转速比r为2.0(自转转速600r/min),EW值分别为0.140和0.149J/s.g。

图2 衬板厚度1mm时对EW的影响
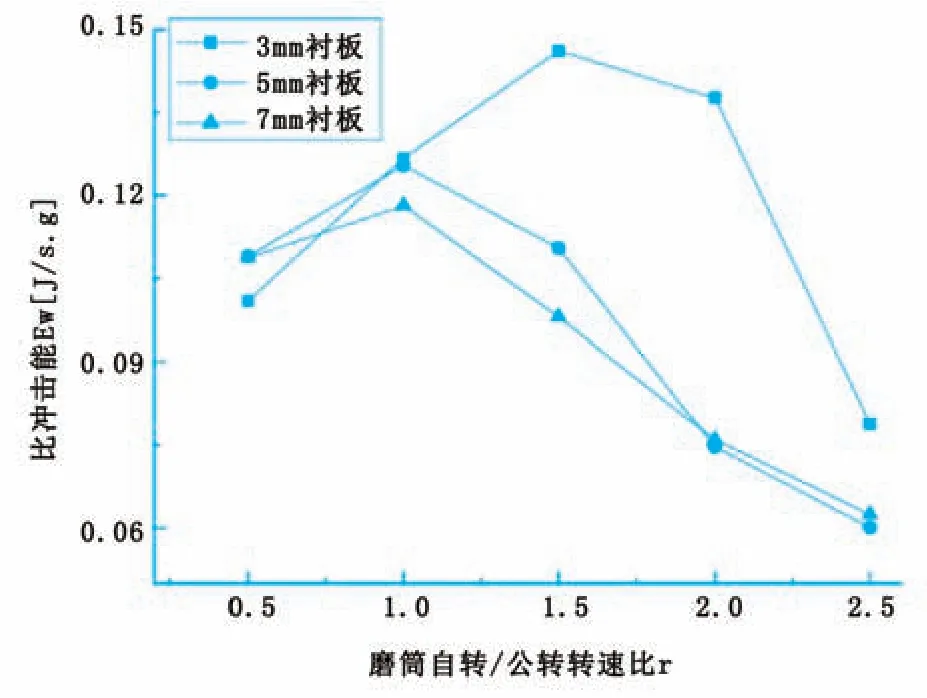
图3 不同衬板厚度对EW的影响
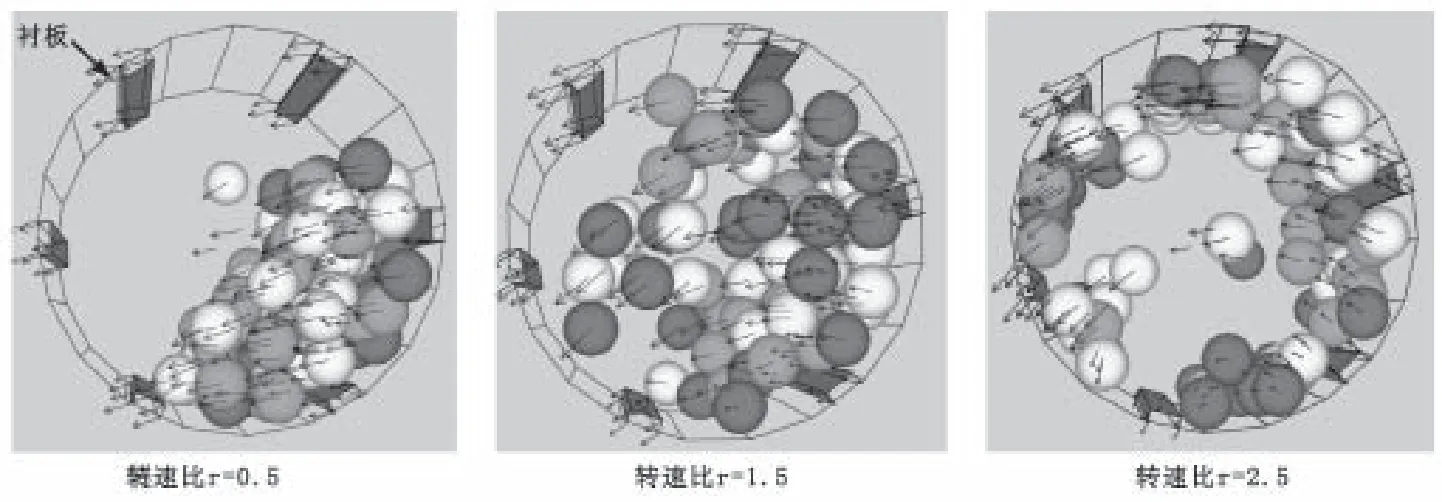
图4 衬板3mm时不同转速比r的钢球运动状态
通过图5曲线,可以明显看出钢球比冲击能EW随着衬板数量而变化的趋势。衬板数量太少或太多,EW明显要小,所以可以确定衬板数量以4¯8块为最佳。
当衬板数=4时,最大EW值(0.149J/s.g)对应的转速比r为2.0,此时的自转转速为600r/min;当衬板数=6时,最大EW值(0.146J/s.g)对应的转速比r为1.5,此时的自转转速为450r/min;衬板数=8时,最大EW值(0.144J/s.g)对应的转速比r为1.5,自转转速也为450r/min。衬板数=4和6相比,虽然前者最大EW值略大于后者,但是前者达到最大EW值的自转转速是600r/min,而后者只有450r/min,故衬板数6要优于衬板数4;以衬板数=6和8相比,前者比后者的EW值大,而自转转速均为450r/min,故前者相对合适,钢球可以发挥较大的比冲击能。
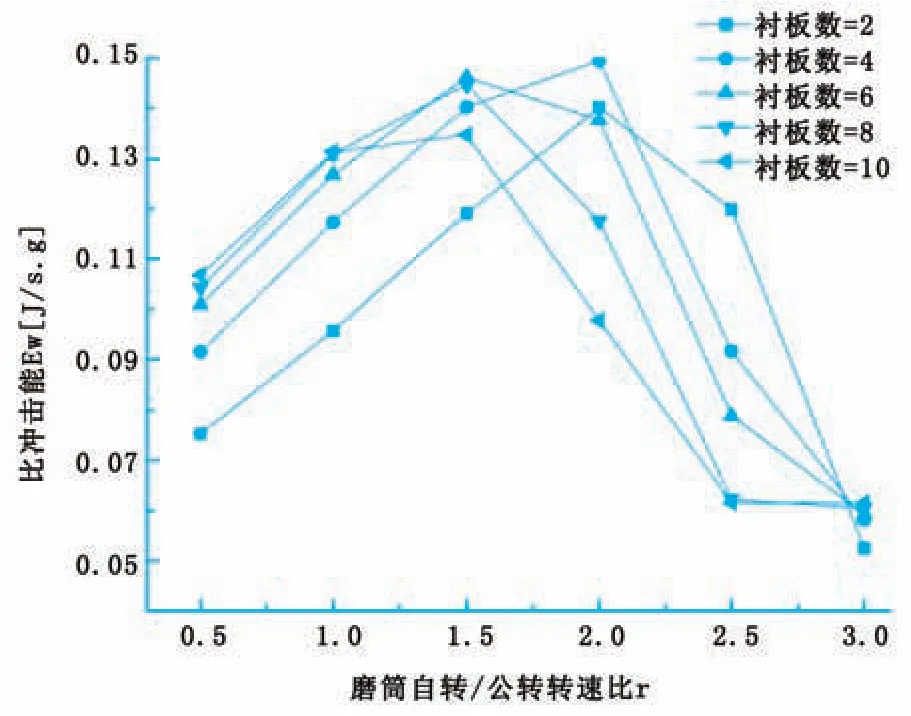
图5 不同衬板数对EW值的影响
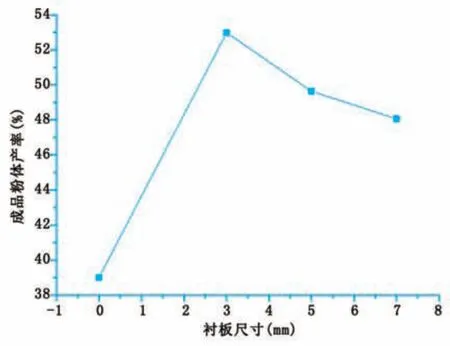
图6 不同衬板对磨机产率的影响
2 实验验证
根据计算机上述模拟,得出行星磨衬板厚度以3mm的钢球的抛落状态最佳,比冲击能也最大,为了验证模拟的准确性,实验验证在单筒φ89×78mm行星磨的条件下进行,分布采用厚度0(无衬板)和3mm、5mm、7mm衬板进行粉磨效率的对比。
对比实验粉磨原料为水泥熟料,密度3.128g/cm3,先经振动筛筛分10min,以粒度4¯5mm颗粒入磨,每只磨筒入磨量150g,粉磨时间5min,公转转速300r/min,转速比1.5。粉磨后卸出磨机进行筛析,按<80μm的通过量来定义成品粉体产率。实验结果见图6。
从图6可以看出,无衬板的成品产率为39%,厚度3mm、5mm、7mm衬板的成品产率分别为52.98%、49.64%和48.06%。说明3mm厚度的衬板是卧式行星磨粉磨的最佳条件,粉磨实验与计算机数值模拟结果相一致。
3 结 论
(1)卧式行星磨加装衬板,可以避免磨内钢球与磨筒之间的相对滑动,在较低转速比下就能取得较大的比冲击能,使得磨内钢球形成良好的抛落状,从而提高粉磨效率。
(2)衬板高度太低,对钢球与磨筒的相对滑动难以改观,衬板高度以3mm为宜,可以在较低转速比下促进钢球的剧烈运动,得到较大比冲击能。随着衬板高度的增加,钢球的比冲击能变小,易出现离心现象。
(3)衬板数量太少时,磨机需要较高的转速比才能使钢球比冲击能达到最大,衬板数=6时,可以在较低转速比下得到最大的比冲击能。衬板数量继续增加,则比冲击能值会逐渐减小。
(4)通过实际粉磨实验验证,证明上述模拟结论与成品产率相吻合,表明离散元法应用到生产粉磨过程具有可靠性和实用价值。
