上证50ETF个股期权的市场效率研究

刘德红，黄振环，陈宗志

(北京交通大学 经济管理学院，北京 100044)

一、引言及文献综述

上证50ETF个股期权于2015年2月9日正式推出，为国内投资者对冲风险、投资获利提供了新的途径。上证50ETF个股期权已经在金融衍生品市场扮演起重要角色，分析其对市场效率的影响作用，对于进一步发展完善国内资本市场有着重要意义。根据Fama(1970)有效市场假说，高效率的市场不存在利用价差进行无风险套利的机会。如果一个市场存在着无风险的套利机会，则该市场的市场效率并非完全有效。

国外关于期权的无风险套利最早是基于期权平价定理(Put and Call Parity，PCP)建立的，该理论由Hans Stoll[1](1969)提出。Billingsley, Chance[2](1985)在PCP定理基础上，提出了盒式价差套利的策略理论(the box spread strategy)。它区别于此前大多运用Black-Scholes原理进行定价效率分析的方法，不需要股票价格和估计股票波动率，模型的前提和假设要求较少，只需要检验市场中是否存在无风险的套利，因此更适用于市场的实证分析。

Joseph, et al[3](2001)运用这一模型验证了市场的有效性，但发现当市场处于压力状态时会有例外。早期关于市场效率的检验，都是在以美国、英国为代表的发达市场进行的。Joseph K. W. Fung，Henry，Kenneth C. K. Wong[4](2004)采用盒式价差套利法检验了恒生指数期权市场的效率，这个市场的特点就是交易薄弱、做市商竞争激烈的新兴市场。Draper, Paul and Fung, Joseph K. W.[5](2002)利用日收益数据，研究了FTSE100 股票期权的交易对现货市场波动性的影响，发现期权交易导致期货市场波动性增加，明显提高了市场效率。Ackert和Tian[6]( 2001)研究了 SPDRs的推出对 S&P500 股指期权市场效率的影响，发现考虑了交易成本和卖空限制情况下，盒式价差条件存在套利的机会。Brunetti 和 Torricelli[7](2007) 分别研究了在牛市价差、蝶式价差和盒式价差下意大利股指期权市场的有效性，并用套利机会的微弱证明了期权市场的有效性。GP Girish, N rastogi[8](2013)在研究印度的指数期权市场效率时运用了盒式价差模型，研究发现随着指数期权的推出，市场内部效率不断提高。

国内由于期权市场起步晚，早期的研究多集中于股指期货与股票定价效率的检验，且多为低频数据，涉及别国市场的才有高频交易数据。熊熊，张宇[9](2011)等运用GARCH模型，研究了韩国KOSPI200股指期权对股市和期货市场波动性的影响，结果表明，期权增大了市场的波动性。林苍祥，邱紫

华，郑振龙[10](2015)采用了台指期权日内高频数据验证了期权市场中散户对于价格预测的重要作用，台湾和大陆同属新兴市场，很多地方有相似之处，为研究大陆的期权市场运行机制提供了研究思路。孙桂平[11](2015)以沪深300股指期权仿真交易为基础，运用期权平价定理研究了套利与市场的效率问题。该研究基于仿真交易进行，得到了较为理想的结论，也为进一步将盒式价差套利与市场效率研究在期权市场的运用提供了参考，但该研究仅局限与仿真交易，并非源于真实市场的数据。

本文以上证50ETF个股期权为研究对象，基于盒式价差套利模型研究了其套利机会的实现。分析投资者能否通过套利获取超额收益，就能对市场有效性进行检验。倘若不存在套利机会，则意味着市场是有效的。通过选取的一段时期内的高频数据，还能够分析套利机会将在何处出现，在此基础上进一步探究其对市场效率的作用，为发展期权市场,提高资本市场定价效率提供实证基础。此外，根据盒式价差套利情况检验市场有效性，进一步验证了以股指期权为代表的金融衍生品在市场定价效率中发挥的功能。

由于分笔高频数据所包含的交易信息最全面最适合进行套利交易的研究，本文采用了上证50ETF个股期权的日内逐笔买卖报价数据作为研究对象，构建盒式价差套利模型，对期权市场是否存在套利机会进行分析，并据此探讨市场的效率问题。

二、实证模型与正态性检验

(一)盒式价差套利模型

盒式价差套利策略由两对具有相同到期日和标的物，但行权价不同的看跌期权和看涨期权组成。低执行价的看涨期权CL多头与高执行价的看涨期权CH多头，高执行价的看跌期权PH与低执行价的看跌期权PL空头，四个期权头寸共同构成了该策略。根据无风险套利原理，最终该策略的损益在|XH-XL|之间，形成了一个箱型，如图1所示。

具体而言，在期初时，套利者付出的现金流为V0=CL-CH+PH-PL；在期末，看涨期权价值应该为VC(ST)=max (0,ST-X)，看跌期权价值为VP(ST)=max(0,X-ST)。因此，到期日的合约价值为

VT=max (0,ST-XL)-max (0,ST-XH)+max(0,XH-ST)-max(0,XL-ST)

(1)

进一步地，若到期日股价上升，看涨期权多头行权，看涨期权空头被行权；看跌期权组合价值为0。合约价值实际为

VT=ST-XL-(ST-XH)=XH-XL

(2)

若到期日股价下跌，看跌期权会行权，同样看涨期权的组合价值为0。此时合约价值实际为

VT=XH-ST-(XL-ST)=XH-XL

(3)

由无风险套利的原理可知，必然会存在V0=VT×e-rt，即我们得到盒式价差套利策略的模型为

CL-CH+PH-PL=(XH-XL)e-rT

(4)

当市场中(CL-CH+PH-PL)与(XH-XL)e-rT不相等时，就会产生套利机会。我们定义价差Spread为

Spread= (CL-CH+PH-PL)-(XH-XL)e-rT

(5)

当Spread<0时，套利者可采取多头盒式价差策略，最终利润为

πL=(XH-XL)-(CL-PL+PH-CH)×erT-M×r×T-C

(6)

上式中的M表示期权的保证金，C为交易成本，r是无风险利率，T为期权组合剩余期限。当πL为正时，意味着套利操作者能够获利。

同理，Spread>0时，可以构建空头盒式策略。该策略下，最终利润为

πS=(CL-PL+PH-CH)×erT-(XH-XL)-M×r×T-C

(7)

(二)正态性检验

虽然正态分布是大多数统计追求的结果，但在金融市场中，许多收益结果往往不符合正态分布，出现的异常值正是我们研究的对象。实证分析中，通过偏度分析、峰度分析和正态性检验来测度数据的正态性。正态性检验的模型有多种，最常用的有Kolmogrov-Smirnov检验、Shapiro-Wilk检验、Gramer-von Mises检验和Anderson-Darling检验[12]。本文考虑到样本数据和稳定性采用Shapiro-Wilk[13](W检验)检验方法。

其原理是用顺序统计量来检验分布的正态性。对研究的对象总体，先提出假设认为总体服从正态分布，再将样本量为n的样本按大小顺序排列，然后由确定的显著性水平α和根据样本量为n时所对应的系数ai，计算出检验统计量W。

统计量W定义为

(8)

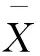
(三)套利的可能影响因素

期权的价值要考虑内在价值和时间价值的影响，虽然上证50ETF个股期权为欧式期权，但是到期期限的长短意味着在到期日前期权所面临的风险是不同的，因此，套利者在套利时会考虑期权到期时间长短这一因素。而上证50ETF期权为做市商的制度，必须考虑其执行价差对于期权流动性的影响，过度虚值状态的期权往往会对期权的流动性产生较大影响，从而影响相应期权的套利行为。最后需要考虑波动率对期权套利的影响，Draper和Fung[4](2002)的研究都发现在期权平价关系的条件下，期权错误的定价的价差程度会随着波动性增加，这意味着市场波动越大时出现套利机会的可能性越高。

在根据期权盒式价差模型模拟套利结果时，必须考虑到期权合约的到期期限长度、期权的内在价值和市场波动率产生的影响，本文将根据这三个方面进行相应的实证检验与分析。

三、数据处理和实证分析

(一)数据处理

本研究基于上证50ETF个股期权展开，使用CSMAR数据库提供的分笔高频数据。选取了50ETF指数个股期权上市后的第六个月，2015年6月1日至7月31日的数据，这段时间的市场还出现了“股灾”这样剧烈波动的状况，对于研究具有一定的参考意义。此外，我们选取了市场波动相对平稳的2016年4月1日至2016年5月30日为样本区间，作为对照期间，共计85个交易日的带有五档买卖报价的日内交易数据。

上证50ETF指数期权采取的是做市商制度，因此，在进行盒式价差套利策略的构造时，首先将行权价和到期日相同的看跌期权和看涨期权进行匹配，拟得到N个不同执行价格的期权对序列：X1,X2,…，XN。

接着，根据到期日将N个期权对两两进行匹配，得到N-1种组合，以此类推。最后N个期权对序列将得到：

(N-1)+(N-2)+…+1=N*(N-1)/2

(9)

式(9)表明，若交易的期权有N个执行价，则相应的盒式价差组合有N*(N-1)/2个，其到期日均为T。因此，不同期限的期权种类，需要重复上述配对过程。

本次研究的无风险利率选取了上海银行间同业拆借利率(Shibor)，在国内的相关研究中Shibor常作为无风险利率的参考标准。表1是本研究所需的Shibor在研究期内各个时期的值，选取了当月1号的利率数值作为无风险利率，并且在期权持有期内，利率的期限结构是平的，排除了利率期限结构的影响。

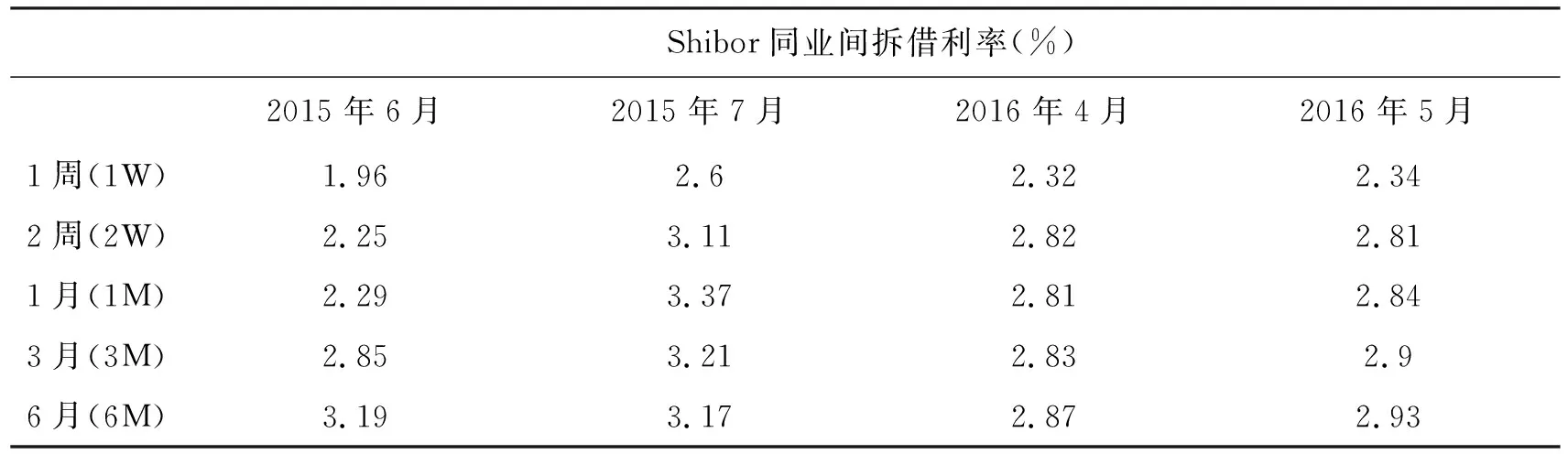
表1 无风险利率

数据来源：全国银行间同业拆借中心官方网站

(二)实证分析

1.持有期限的影响

期权的时间价值使得远期合约通常比相同执行价的短期合约价格更高，而且其保证金的机会成本也高。本次研究中，短期合约的持有期为1-7周，中期合约为8-12周，远期合约为18-22周。分析持有期限对套利机会的影响时，选取2016年4月1日至2016年5月30日的数据。

表2展示了不同持有期限的盒式价差(spread)的统计分析结果。在448 704对套利组合中，短期、中期和远期合约价差(spread)的平均值分别为-0.000 2、0.000 5和0.001 4，远期合约价差的均值相对较高。在这些配对组合中，能够从套利中获利的比例分别为0.49%，0.59%和0.71%，即远期合约套利获利的机会更多。但考虑到远期合约会占用更多的保证金成本后，套利次数的增加并不能从均值上简单得出，我们需要进一步验证价差分布的正态性。如果价差值的分布是服从正态分布的，意味着套利获利的可能性极小，市场效率较高。

这一点从我们绘制的spread的直方图(图2)中能够得到直观的反映，但图形得到的结果只能是估计状况，为了研究的严谨性必须进行正态性检验。我们运用W检验，具体模型已经给出。模型中X(i)为价差spread按从小到大顺序排列后的数据组，最终检验得到的结果见表3。可以看到，近期、中期和远期合约的p值均为0，意味着原假设被拒绝，也即套利机会的分布并不符合正态分布。

对比直方图能够看出，价差spread的分布接近正态分布，短期和远期合约的图形边界较为粗糙，可能存在“厚尾”(Fat tails)特性，远离期望的区间有较多异常值分布。图3所示的是三种合约的分位数图，图中的斜线为标准正态分布。盒式套利价差(Spread)的分位数值偏离了斜线，与标准正态分布的形态不符，有许多值低于和高于斜线分布在其左右两侧，表明价差具有“非正态性”，观测到的异常值远多于正态分布应有的呈现情况，价差的分布存在“厚尾”(Fat tails)特性。从分位数图可以看出短期合约和远期合约的异常情况稍微多于中期合约，但是差距并不明显。

“厚尾”的存在意味着盒式价差的绝对值与0均值偏离得更严重，这暗示着“厚尾”部分的异常值反映了套利机会的存在。基于此，我们进一步预测了“厚尾”部分异常值是否存在套利机会。

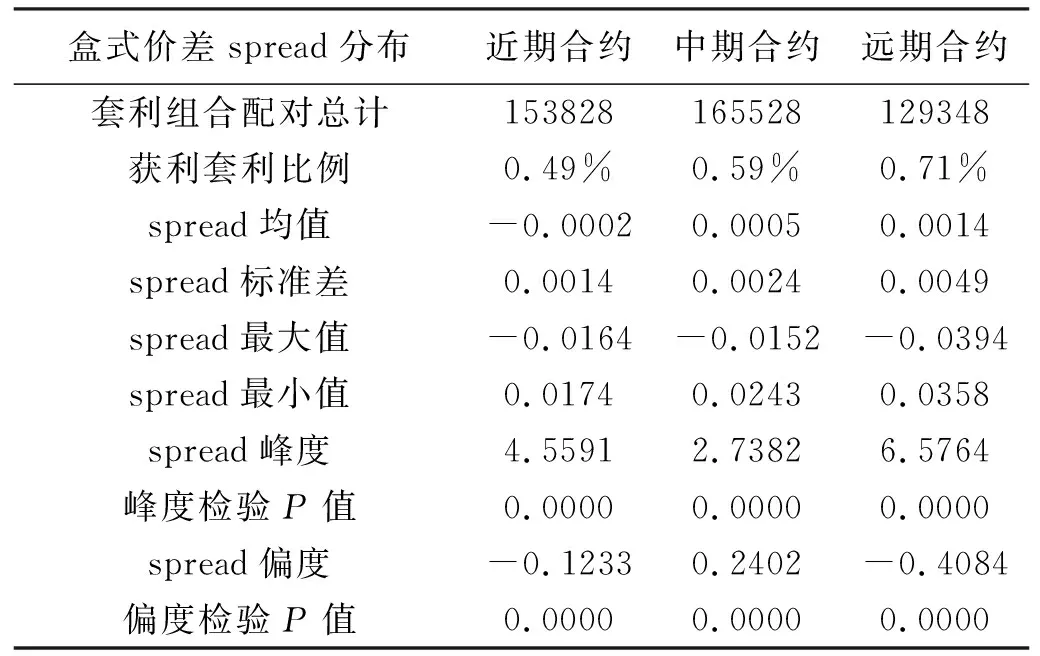
表2 盒式价差spread统计结果

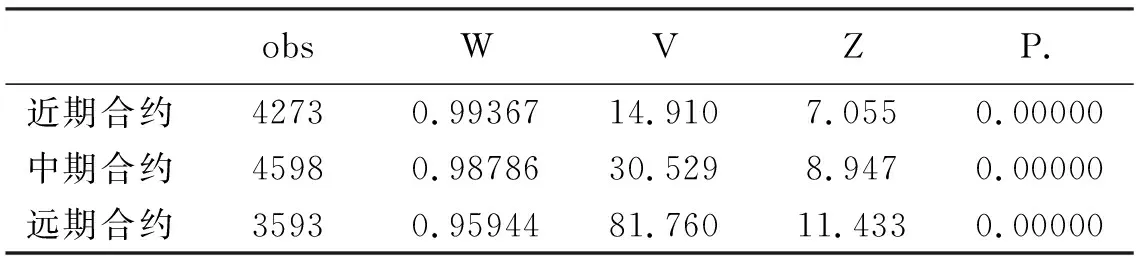
表3 正态检验(W检验)

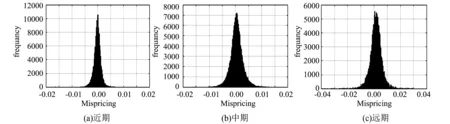
图2 近期、中期和远期合约Spread直方图

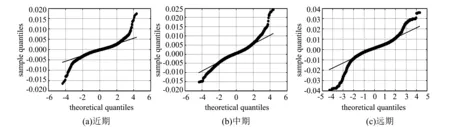
图3 近期、中期和远期合约分位数图

2.内在价值的影响

为了避免市场波动对我们分析期权组合内在价值对套利的影响造成的干扰，在研究执行价差对套利的影响时，选取2016年4月1日至2016年5月31日这个波动较为平缓的区间。由于样本期内50ETF的市场价格在2.1左右上下波动，因此，选取的期权组合为相同期限的行权价从1.9至2.3元的期权，以低行权价期权为基础，分别和其他组合配对，构造行权价差为0.05及其倍数的不同套利组合。

为了便于分析套利机会的产生，将组合头寸的内在价值计算设定为

(10)

V值越大，表明期权组合处在深度实值或者深度虚值状态。表4包含186962对已完成匹配的期权组合，将其按照对应内在价值进行分组，得到了相关的统计结果。定义0-2.5%的V值期权组合为平价期权，2.5%-10%为实值或虚值状态期权，10%-20%的期权则处于深度虚值或实值状态。

根据表4的统计结果可知，期权组合的内在价值越偏离平值状态，盒式价差值越大，期权组合套利的可能性就越高。为了进一步验证这一结论，设立了如下的方程：

Spread=α+β1·ATM+β2·OTM+ε

虚拟变量ATM取1时，代表期权组合处于平价状态，若为非平价期权，则ATM值取0；虚拟变量OTM作为深度虚值和实值状态的期权的指标，即内在价值V取值范围为10%-20%时，OTM值取1，其余时候取0。根据已有的相关spread的值进行回归分析，得到结果见表5。

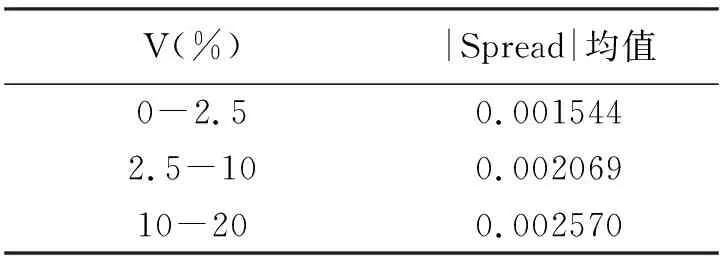
表4 期权内在价值对价差的影响统计分析

表5 回归分析

根据回归分析可知OTM值的统计检验最具显著性，意味着当期权内在价值处在深度虚值和深度实值状态，即内在价值较高的状态时，整个套利组合的价差更容易出现。而平价状态的期权最不容易出现套利可能。

3.波动率的影响

我们记PL和PS为考虑交易成本后的多头、空头套利利润。异常值多出现在期权市场价格波动程度较大的时期，尤其是2015年7月8日和7月9日两天。实际中，这两个交易日是2015年资本市场第一轮快速下跌期的最后两天，市场恐慌情绪达到极点。而诸如2016年4月1日至2015年5月31日这样的市场平稳期内，其套利价差Spread分布则比较均匀，因此将波动期与平稳期的盒式价差套利组合进行对比，以判断异常值的出现是否意味着套利机会的实现。表6反映了波动期和稳定期中单次套利利润较高的套利机会统计结果，σ和σP分别是CLP模型和Parkinson模型计算出的该交易日波动率。

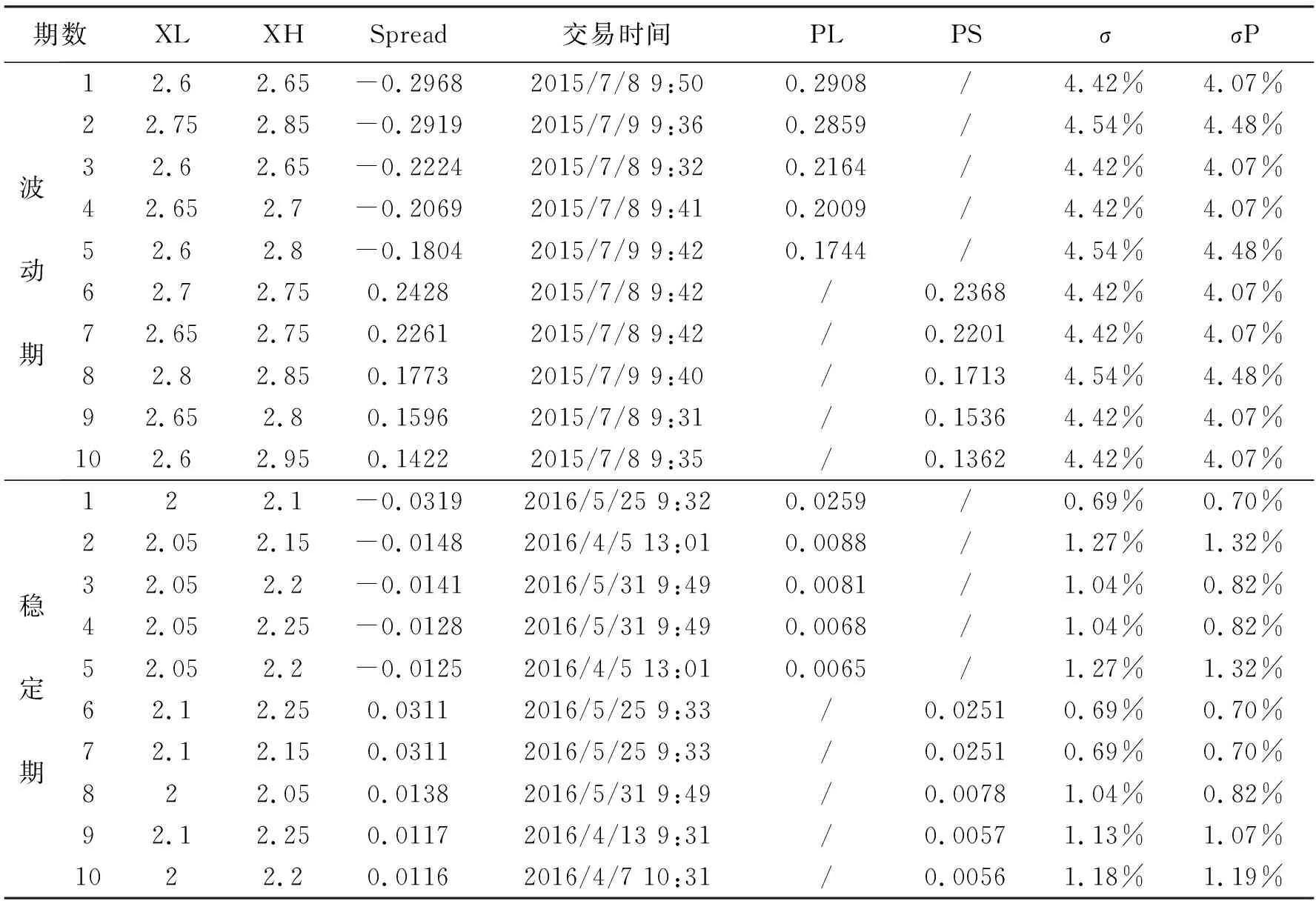
表6 波动期和稳定期套利机会统计

结果发现，期权市场在这两个交易日内频繁出现套利机会。尤其是在开盘后半个小时内，产生了大量的高利润套利机会，这也是之前关于价差值分布统计中的“厚尾”部分的异常值。相比之下，稳定期内套利机会多出现在上午和下午刚开盘时，但其价差值逐渐趋于平稳，套利利润也明显下降，在考虑交易成本和时间价值后，套利机会降低。

在市场波动剧烈的情况下，套利组合的价差值会整体增加，它们造成了价差分布中的“厚尾”异常值；甚至随着波动率的增加，价差迅速扩大导致套利机会频繁出现。而在市场较为平稳时，价差值整体较低(绝对值小于0.002)，趋于正态分布的水平，并随波动率的降低而下降，套利利润约为高波动期的十分之一，未出现过于显著的套利机会。

我们将两个时期的波动率和盒式套利价差绝对值的日平均值绘制其趋势图(图4和图5)，可以进一步对比市场波动期和稳定期盒式价差套利的机会变化，以及其余波动率的联系。

图4 波动期|spread|趋势

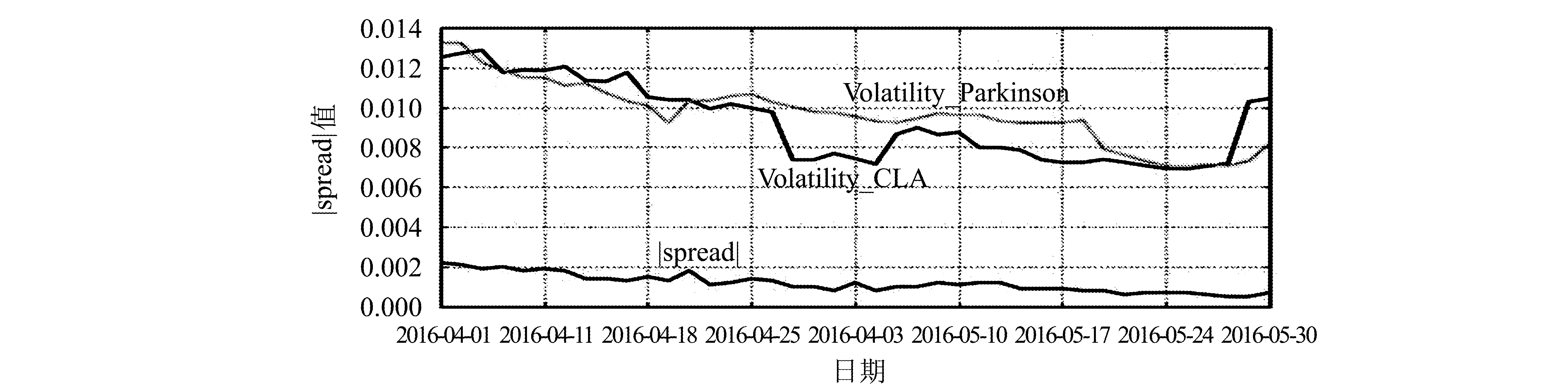
图5 平稳期|spread|趋势

从每日|spread|的走势曲线看，价差在平稳期变动平稳，而在波动期则呈现出迅速升高的趋势。结合两个时间的趋势图可知，在市场波动剧烈的情况下，盒式价差套利的日平均值会快速上升，这意味着市场剧烈波动时期，会有频繁的套利机会产生。而在市场较为平稳的情况下，spread值整体处在较低状态，介于0-0.002之间，并随着波动率的走低而趋于下降，无异常波动值的出现。

4.日内效应

异常价差值的出现即为套利机会的产生，因此，研究何时出现异常值能够为我们判定套利机会的时机提供帮助。我们用稳定期内的远期合约产生的盒式价差数据(共3593个)为样本，得到了交易日内期权套利的分布散点图(图6)。从图6可知，临近开盘时刻的spread值分布较散乱，异常值多；同样，中午收盘和下午开盘时亦存在较多异常值。这与我们之前的分析相吻合，即在市场开盘和收盘的临近时点会出现较多的套利机会。此外，可以看到的是spread值越大，意味着投资者套利获得的利润也越高。

根据日内价差的分布图可知，在期权市场上午刚开盘时进行盒式价差套利可获得较高利润，上午闭市前最后半小时和下午开市后的半小时，套利机会和利润次之。而在其他时间内spread分布较均匀密集，套利的超额利润几乎不存在。

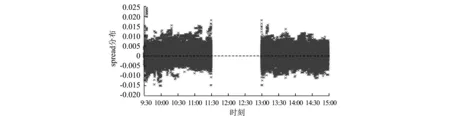
图6 Spread日内分布散点图

四、研究结论与启示

本文以国内首只场内交易的个股期权为研究对象，检验期权市场是否存在套利，以此验证市场的有效性。研究基于盒式价差套利策略，对上证50ETF个股期权在2015年6月1日至7月31日和2016年4月1日至5月30日的高频分笔交易数据进行实证分析。首先构造了盒式价差套利模型，并运用实际交易数据进行模拟得到套利价差的分布状况；进一步从期权的到期时间、内在价值和波动率三个角度进行研究，分析了在上述不同性质的影响下期权市场套利的可能性；最后在前文研究的基础上分析了期权的日内效应，研究套利最可能出现的时点。结论表明，在考虑交易成本及买卖价差以及50ETF的分红后，排除市场剧烈波动的个别交易日，其他时间市场中能运用盒式价差策略进行套利的机会很少，即50ETF期权市场在大多数情况下具有较高的市场效率。

本研究的主要贡献在于证明期权市场的有效性，明确了内在价值、到期时间和市场波动性对于期权套利机会的影响。这为市场监管者带来了积极的启示意义，即期权市场的发展能够促使资本市场价格回归理性，而且由于期权能够方便进行套利组合和对冲保值策略，并突破股票卖空的限制，期权的发展能够活跃资本市场，并且其较好的定价效率也有助于纠正错误定价。

本文的启示：对于投资者而言，上证50ETF个股期权市场效率较高，进行套利交易的机会不多，但期权的内在价值、到期时间和市场波动性会对套利机会产生不同的影响。对于机构投资者来说，目前期权合约交易不够活跃，交易频率较低为机构投资者创造了套利的机会，此外也能够通过培养专业交易人员、优化套利模型等方法进行套利；而对于个人投资者而言，由于上证50ETF个股期权市场整体有效性较高，且期权保证金及交易准入门槛的限制，进行投机炒作的机会较少，因此，个股期权是较为可靠的套利保值工具，可用于对冲股票市场的风险。总之，期权市场的有效性有助于引导理性投资，促进多层次资本市场良性发展。