陕南乡村聚落街巷曲折特征分析研究

杨涛

以陕南乡村聚落为例，采用量化分析的研究方法，从街巷的转折点数量、偏离距离、直线率等几个方面，对陕南乡村聚落街巷曲折形态特征进行了量化分析，为研究和分析鄉村聚落街巷形态特征提供了借鉴思路。

引言

乡村聚落形态是乡村在适应自然环境条件下和实现自身生产和生活需求的物化体现，“主要表现为村落平面的形式和村落在空间高度上的形态”，是构成乡村聚落不同层面形态要素的表现形式和结构特征的反映。街巷作为乡村聚落的骨架要素，是乡村聚落形态的重要组成部分。在适应所处的自然地理条件的演变过程中，乡村聚落的街巷形态呈现出有别于城市道路整齐划一的形态，呈现出明显的曲折多变的形态特征。

虽然曲折性是乡村聚落街巷形态的重要特征，但现有的理论研究中对乡村聚落街巷曲折特征的研究数量较少，理论研究的缺失使乡村建设对乡村道路的建设只能照搬城市建设的经验，按照城市的街道进行处理，呈现出整齐划一的形态特点，乡村聚落街巷自身的特色逐渐缺失。乡村的形态和面貌越来越呈现出和城市相同的趋势。而作为记忆载体的物质条件的改变也使“记得住乡愁”的美好愿望成为无根之水，无本之木。

因此重新准确认识乡村街巷区别于城市街道的曲折特征，有助于抓住乡村形态特质，从而保护和延续乡村特有的风貌，避免城乡面貌的趋同化，使“乡愁”真正留得住，对乡村的记忆持久弥新。基于此，本研究以陕南部分乡村聚落作为研究对象进行考察，对其街巷的曲折特征进行研究和分析，归纳和总结乡村聚落街巷形态曲折特征的规律和原则，为后续的新农村建设保持和延续乡村自身特色提供一定的借鉴和参考。

一、研究对象与研究方法

（一）研究对象选择

本文以陕南地区的10个乡村聚落为研究对象，通过研究对象的地形图、卫星影像图，结合现场调研，对聚落街巷形态的数据进行整合与校准，在此基础上绘制研究所需要的矢量图形。

（二）研究方法

1.街巷的分级

乡村聚落作为一种自发性形成的聚居点，形态不同于城市，有明显的先导性和规划性，为了较准确地分析这种自发性在街巷不同层级构成的曲折特征的差异，有必要对街巷构成进行合理分级。自然界中河流的形成就是一种自发性成形的线性要素，构成方式和生成机理和乡村的街巷存在一定的相似性，因此本文街巷分级的方法，借鉴了河流分级中的Horton法对研究对象的街巷进行分级。以直接连接住户，最小不分支的街巷为第一级，仅仅接纳第一级街巷为第二级，接纳一二两级街巷的为第三级，依次类推，如图1所示。

2.研究指标选取

规划领域中对街巷或道路的曲折特征主要关注于其大的曲折趋势，即街巷或道路的实际距离与直线距离之间的关系，并不关注其形态在微观层面的曲折变化规律。因此本研究为了深入分析乡村聚落街巷的曲折特征，除利用常规的道路直线率（见式1）来表征街巷的曲折特征外，还需要利用其他指标较为准确地反映街巷的曲折特征变化。

直线率公式：T=l/L（1）

其中，T为街巷直线率;l为街巷端点直线距离;L为街巷实际长度。

乡村聚落的街巷可以近似地看作是若干条折线组合而成。这些折线的弯折变化和街巷两个端点所形成的连线存在偏离的变化可以用来反映街巷的曲折变化程度。这种偏离变化可通过若干转折点以及这些转折点与街巷端点连线的距离来表征。因此本文以这种模型里出现的街巷转折点数量（Nz）、最大偏离点距离（Dmax）和最小偏离点距离（Dmin）以及最大偏移距离和最小偏离距离差值（?D）作为反映街巷曲折度的补充研究指标（见图2），和规划中常用的直线率共同描述乡村聚落的街巷曲折变化。

3.数据分析方法

按前述分级方法将研究对象的街巷进行分级，分别统计其街巷曲折特征各指标的最大值、最小值、平均值和变异系数，以这些特征值来比较不同级别街巷的曲折特征的差异，并通过拟合回归方程的方法来分析乡村聚落街巷曲折特征变化和街巷级别的关系。

二、结果与分析

（一）街巷曲折特征差异

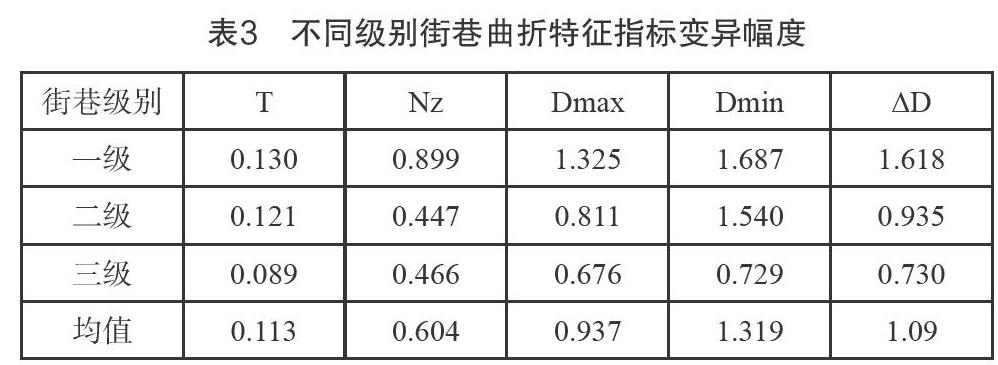
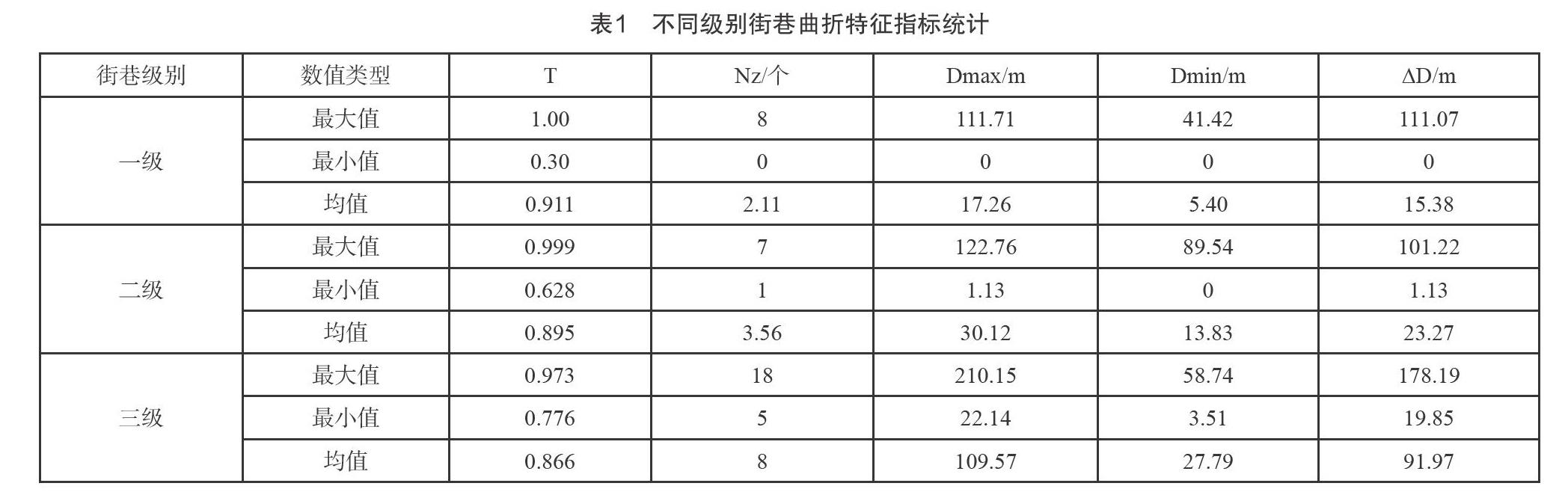
通过本次研究发现，陕南乡村聚落街巷不同级别的街巷在转折点数量、最大偏离距离、最小偏离点距离以及偏离距离差值有较大差异，而直线率的差异在4种曲折特征指标中最小（见表1）。其中，转折点数量均值最小的街巷级别为一级街巷数量，仅为2个，最大为三级街巷转折点数量多达10个，为一级街巷的5倍，表明三级街巷比一级街巷有更多的转折。最大偏离距离均值中最小的是一级街巷为17.91m，三级街巷的最大为109.57m;最小偏离距离均值最小仍然是一级街巷为0m，三级街巷的最大为17.60m;偏离距离的差值最小仍为一级街巷，最大为三级街巷。这表明在街巷级别中，三级街巷相对于一级街巷，不仅有着更多的转折点，而且转折幅度也远远大于一级街巷，从外观上表现出较大的曲折变化，这一特点也反映在直线率指标中，一级街巷的直线率（0.911）大于三级街巷的直线率（0.866）。

通过研究发现，各指标中，转折点数量、最大偏离距离、最小偏离距离及距离差随街巷级别升高而增加，直线率则随着街巷级别的升高而降低。这表明随着街巷级别的升高，街巷的曲折程度表现出变大的趋势。通过对各曲折度指标数据的回归分析也可以发现相似规律，街巷各曲折特征指标与街巷级别的关系均可用二次函数来表征。其中除最小偏离距离外，其他各指标伴随着街巷级别的升高均为增长趋势。从回归方程系数的差异，可以知道伴随着街巷级别的升高曲折度的各指标的增长幅度并不一致，指标中距离差和最大偏离距离增长最快，直线率增长最慢（见表2）。

（二）街巷曲折特征的变异程度

前文用各曲折度指标的平均值进行了比较，但均值只能反映数据的集中性，无法反映数据的多样性，因此还需要借助其他指标来反映街巷曲折度的指标变化幅度。变异系数可以用来比较不同指标数据的变化幅度的大小，变异系数大，则该指标数据的变化幅度大、多样性高;反之则说明该指标数据的变化幅度小，多样性低。变异系数的计算公式为：变异系数=标准差/平均值。通过研究发现街巷曲折度各指标的平均变异系数顺序为直线率<转折数量<最大偏离距离<距离差<最小偏离，各形态指标中直线率、转折点数量的变异系数最小，均值分别为0.113和0.604（表3）。说明在曲折度各指标中，直线率和转折点数量较为稳定，数据的变化幅度小;而偏离距离的极大值、极小值和差值3组指标的变异幅度较大，均值在0.9以上，说明它们的数据变化幅度大，最不稳定。不同级别的街巷形态指标的变异程度也不相同，从表3中可以看出伴随着街巷级别的升高，各曲折度指标的变异系数均成下降趋势，表明随着街巷级别的升高，各曲折度指标数据趋于稳定，变化幅度减少。通常情况下，变异系数不大于1，但本次研究中的一级街巷的最大偏离距离、最小偏离距离和距离差值均出现了大于1的情况，说明这3个指标的数据波动较大，数据的均匀性交叉，也较为客观地反映了现状中街巷为适应外部条件所发生的变化。

三、讨论与结论

乡村聚落的街巷在适应乡村所处的自然地理环境下，形成其特有的结构系统，加之乡村聚落的形成是一种自发性行为，因此街巷形态区别于城市街巷那种整齐划一的形态，呈现出曲折变化的特点。

不同级别的街巷曲折特征的差异从一定程度上反映出其在聚落街巷体系中承担的交通联系功能的差异。低级别的街巷主要起到居住组团内部的交通联系功能，如一级街巷主要和住户连接，为减少居民从家到各道路的行走距离，使住户便捷地达到各道路，其形态尽量平直;而高级别的街巷要承担组团之间的交通联系功能，尤其在分布在用地条件明显受到限制的山区、河谷的乡村聚落，其组团分布较为分散，连接各组团之间的高级别的街巷除了长度增长外还要适应组团间的各种地理环境条件，曲折特征要明显大于低级别的街巷。在本研究中曲折特征指标的差异也表明了这种功能上的差异，随着街巷级别的升高，各级街巷的转折点数量、最大偏移距离、最小偏移距离和偏离距离的差值均值在增加，直线率在降低，表明高级别的街巷由于功能因素在形态上显得更为曲折，或者说曲折的幅度更大。而对比各指标的差异可以发现，不同级别的街巷中，直线率的差异是最小的，说明在条件允许的情况下，尽量将街巷路网组织成接近直线类型，减少交通距离是乡村聚落街巷组织的理想目标，差异较小的街巷直线率也是乡村自发性建设中，平衡经济利益和适应外部条件的一个相对均衡的选择结果。

本研究通过各指标的变异系数研究发现，各指标中除直线率外，其余各指标的变异系数均较大，表明相关数据的均匀度较少，也反映了不同条件的乡村聚落由于自身条件差异的巨大变化。指标中偏离距离的变异幅度较大，转折点数量的变异幅度较小，说明乡村聚落在进行街巷建设时，受制于适应地形条件只能首先通过增加偏离距离来获得对外部条件的适应，使偏离距离数据的离散程度要大于转折点数量，这是在适应外部条件下一种人为选择的体现。

综上，乡村聚落的街巷曲折变化是在适应外部自然地理条件时，通过一定的人为选择实现的。本研究的结果限于研究条件，没有将具体的自然地理条件，如坡度、坡向等与街巷的曲折特征指标进行关联分析，对街巷究竟在何种条件下会发生何种变化认识不够深入，还需要在后续的相关研究中进行验证和分析。

（作者单位：陕西理工大学土木工程与建筑学院）