超高压容器设计实例浅析

(惠生工程(中国)有限公司， 上海 201210)

随着化学工业、石油工业、人造水晶、合成金刚石、等静压处理、超高静液压挤压、粉末冶金、金属成型以及地球物理、地质力学研究的发展，超高压容器越来越成为十分重要的、不可缺少的工具和各行业进行学术研究、产品生产和试验的必备设备。

为避免锅炉和压力容器设计不慎引起的破坏事故，确保高压、超高压容器的安全可靠使用，压力容器设计规范、规程、制造与检验技术规定一直在不断地完善、制订或修订[1]。我国于1993-12颁发了《超高压容器安全监察规程》(试行)[2]，该规定于2004年修订为TSG R0002—2016《超高压容器安全监察规程》[3]，并于2016-02-22合并到TSG 21—2016《固定式压力容器安全技术监察规程》[4]，GB/T 34019—2017《超高压容器》[5]紧跟其后于2017-07-12发布，2018-02-01正式实施，这标志着设计压力大于或等于100 MPa、设计温度在-40～400 ℃的超高压容器的选材、设计、制造、检验和验收都有了相应的标准，为设计人员提供了理论依据。虽然标准的颁布实施在设计上有了根据，但标准的设计实例还没有发布，超高压容器的设计计算还处在对照标准阶段，尤其在某些细节的处理上，标准并没有做出详细的规定。本文以1个超高压容器的工程设计为实例，介绍超高压容器的计算，供相关同行做一参考。

1 超高压容器设计参数[6-7]

某工程项目超高压容器结构简图见图1。此设备结构为筒体+螺塞型式，专为在水下20 000 m进行的实验而设计。

1.螺塞Ⅰ 2.O型圈Ⅰ 3.转换接头Ⅰ 4.筒体 5.转换接头Ⅱ 6.O型圈Ⅱ 7.O型圈Ⅲ 8.螺塞Ⅱ

该设备材料大部分为锻件，筒体为整体锻造结构，因材料原因不能采用焊接结构，只能采用螺纹连接。设备工作压力pw=200 MPa，设计压力ps=220 MPa，工作温度tw=1～50 ℃(外表面温度)，设计温度ts=50 ℃(外表面温度)，工作介质为淡水，内径d=300 mm，外径D=570 mm，标准筒体长度L=1 000 mm，标准有效体积V=706.5 L，腐蚀余量C=1 mm，使用寿命20 a， 循环次数3 000次，主要受压元件材料为35CrNi3MoVR。

2 超高压容器设计计算[8]

对超高压单层厚壁圆筒，按大变形理论根据爆破压力来设计较为合理。但这些公式的运算十分冗繁和复杂，因而一般工程上大都采用Faupel经验公式。试验压力按下式计算：

3 超高压容器强度校核

依据设备的结构特点和使用工况，选取塑性垮塌、局部过度应变以及疲劳失效评定方法对设备的强度进行校核。考虑筒体端部及螺塞为螺纹承载，按GB/T 34019—2017《超高压容器》 附录D校核筒体端部环向截面的当量应力，参照GB/T 34019—2017《超高压容器》附录D对筒体和螺塞的螺纹强度进行强度校核，采用疲劳分析法对螺纹牙进行疲劳评定。

3.1 塑性垮塌失效评定[5，9]

采用爆破压力法，按材料拉伸试验数据进行计算。当圆筒形筒体承受内压力超过屈服强度进入塑性状态后，筒体器壁发生应变硬化，可相应地提高承载能力，但器壁在获得硬化效应的同时，厚度也相应地逐渐减薄。开始时强化作用是主要的，承载能力得到提高。到一定值时，由于变形的加大，器壁减薄的作用增加，承载能力反而略有降低，筒体就在较低载荷下发生爆破。在整个过程中，出现的最大承载能力称为极限承载能力。爆破时的内压力为爆破压力，爆破压力是在维持较长的时间下达到破坏的最低压力值。

应变硬化的作用和壁厚减薄的影响情况极为复杂。为了简化分析，假定体积不变，即器壁断面保持不变并忽略轴向应变。经过剖分圆筒形筒体在塑性变形得到充分发展而即将达到极限压力时，对其横截面进行精密测量，结果表明断面积几乎无变化，这证明体积不变的假定是可行的。同时，应变测量表明轴向应变很小，不及周向应变的1%，可以忽略不计。所以，轴向应变为0的假设也是可行的。爆破压力pb按下式计算：

爆破安全系数nb按下式计算：

带入相关参数计算，得nb=3.0>2.2，满足强度要求，评定通过。

3.2 局部过度应变失效评定[10]

3.2.1材料应力-应变曲线

依据GB/T 34019—2017《超高压容器》附录E绘制35CrNi3MoVR材料的真实应力-应变曲线，见图2。

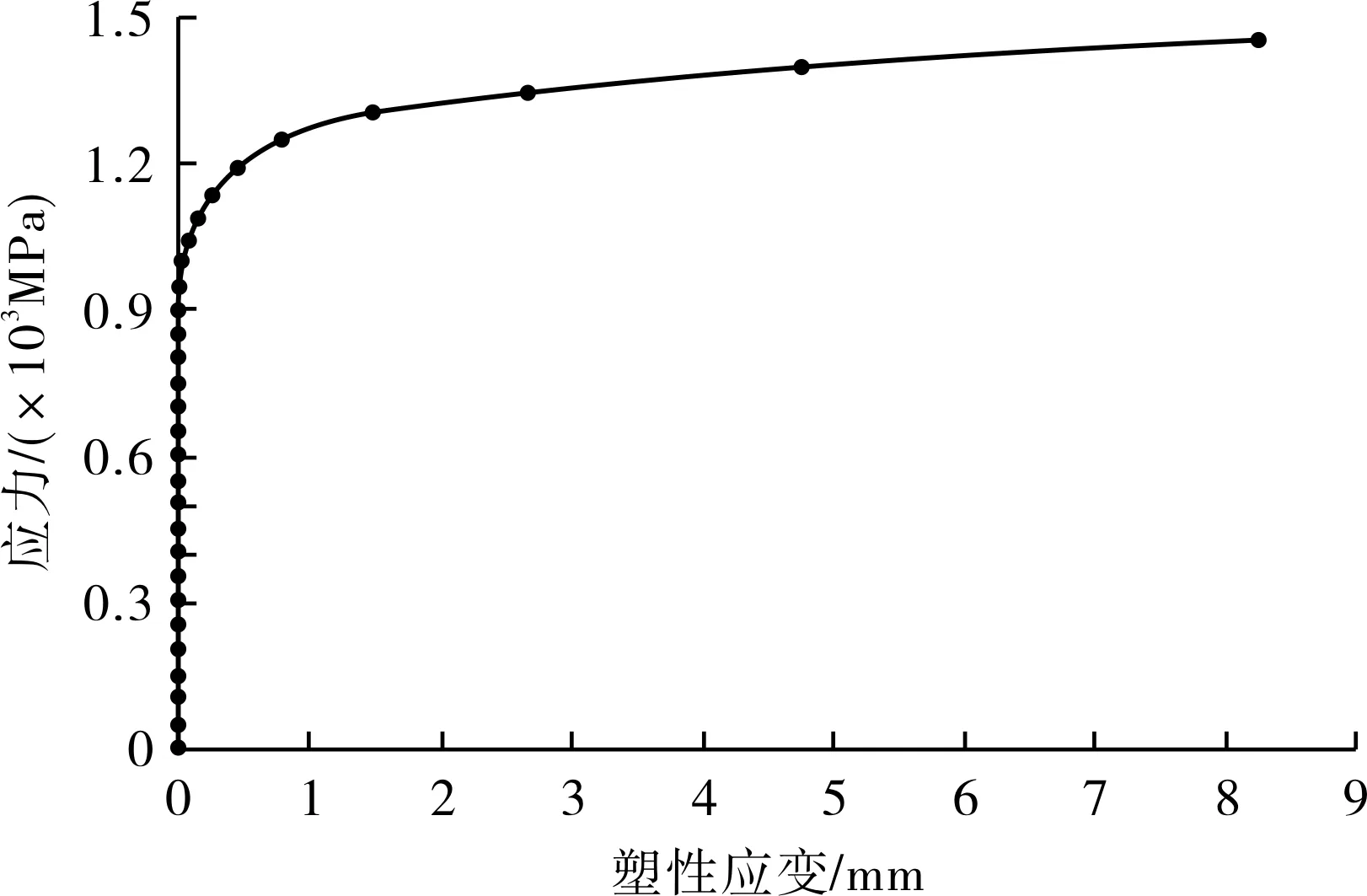
图2 22 ℃时35CrNi3MoVR材料真实应力-应变曲线

3.2.2建立有限元模型

经计算对比，左侧筒体及密封塞应力稍大于右侧筒体及密封塞，因此只针对实例左半侧进行分析。应用有限元分析软件Ansys workbench 14.0，对筒体及密封螺塞建立1/4模型(左侧)并进行网格划分，见图3。

图3 容器左侧1/4模型及网格划分效果图

3.2.3载荷工况和弹塑性数值计算

设计工况下载荷p1=1.42p=1.42×220=312.4 MPa。

在材料属性中添加真实应力-应变曲线，在所有受内压的筒体及密封塞内表面施加塑性垮塌失效压力载荷(440 MPa)并考虑几何大变形，数值求解计算得到的左半侧容器位移收敛解见图4，当量应力(Von Mises应力)收敛解见图5。

图4 左半侧容器位移云图

图5 左半侧容器Von Mises应力云图

在弹塑性数值计算分析时，程序解析提取312.4 MPa(整个加载时长的0.71倍)时的计算结果作为局部过度应变失效弹塑性分析的评定依据。312.4 MPa下左半侧容器的当量塑性应变见图6。

图6 312.4 MPa下左半侧容器当量塑性应变

3.2.4应变极限计算及合格判定

容器任意部位的三轴应变极限为：

式中，εL为三轴应力状态对应的应变极限；σ1、σ2、σ3为主应力，σeq为当量应力，MPa。

容器任意部位的当量塑性应变εpep均满足εpep≤εL，评定通过。

3.3 疲劳失效评定

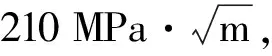
根据计算，裂纹扩展至临界裂纹深度ac(73.38 mm)的总循环次数Np=13 472，裂纹扩展至ac/4时的总循环次数Nc=10 984。因此容器在0～200 MPa下的许用循环次数Na=min{Np/2,Nc}=6 736。

表1 循环计算部分结果

3.4 筒体端部、筒体螺纹及螺塞螺纹强度校核

按GB/T 34019—2017《超高压容器》附录D进行筒体端部、筒体螺纹及螺塞螺纹强度校核，文中不再详细介绍。

3.5 筒体螺纹及螺塞螺纹疲劳评定

3.5.1载荷工况

根据设备的使用情况，有3种工况，即0～40 MPa、0～200 MPa、0～246.4 MPa。

3.5.2弹性数值计算

利用Ansys workbench 14.0进行弹性分析，模型中考虑筒体螺纹与螺塞螺纹之间的摩擦。0～246.4 MPa工况下的筒体端部第一主应力云图见图7，螺塞第一主应力云图见图8。

图7 0～246.4 MPa下筒体端部第一主应力云图

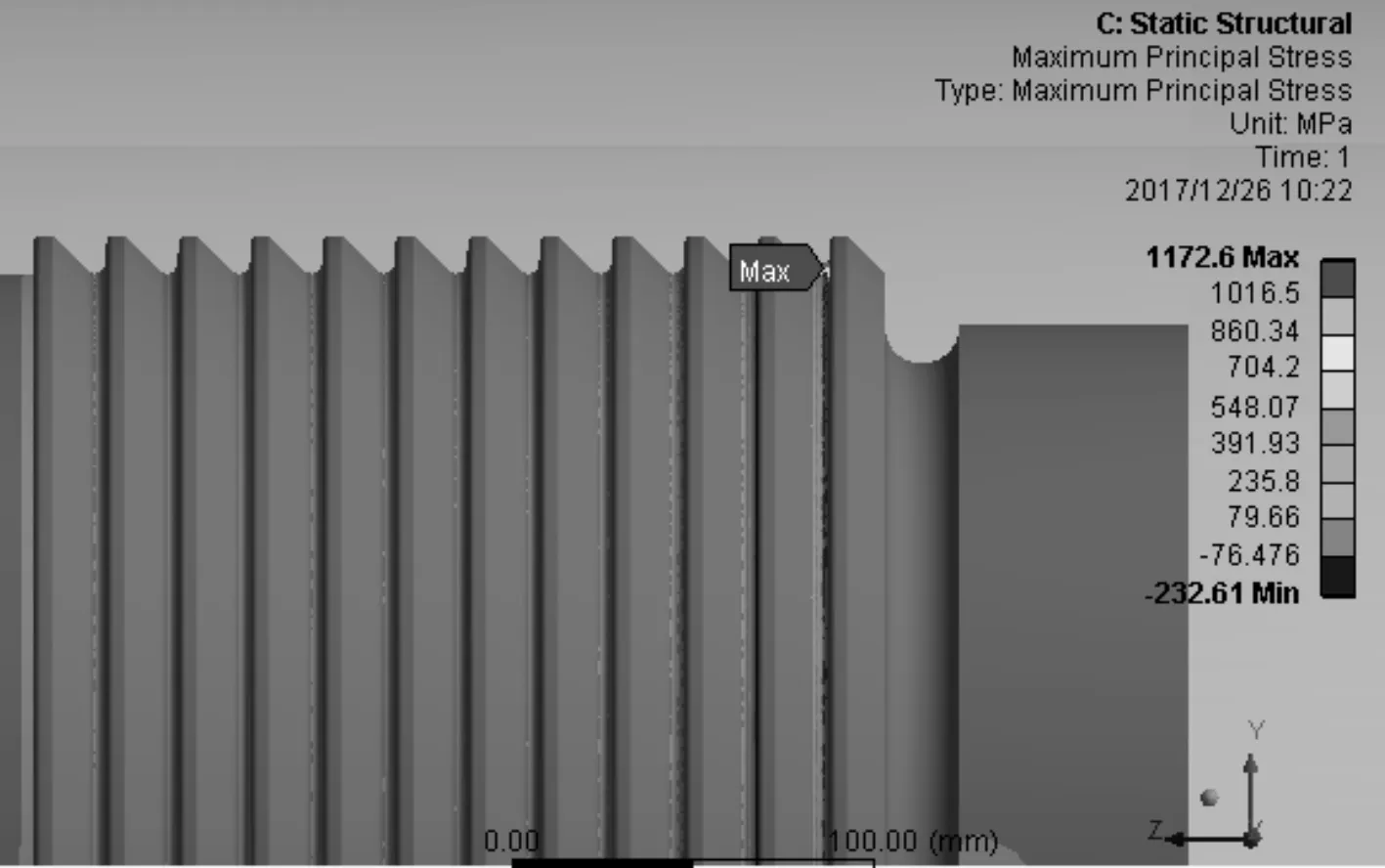
图8 0～246.4 MPa下螺塞第一主应力云图

3.5.3确定交变应力强度幅

按下式计算主应力差Sij：

按下式计算交变应力幅Saltij：

Saltij=0.5(Sijmax-Sijmin)

按下式计算主应力和Snij：

按下式计算主应力和均值Snijm：

Snijm=0.5(Snijmax+Snijmin)

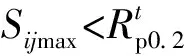
按下式计算当量交变应力幅Seqij：

最后按下式计算当量交变应力强度幅：

Seq=max{Seq12,Seq23,Seq31}

由图7及图8可以看出，筒体螺纹最大应力大于螺塞螺纹最大应力，因此只需对筒体螺纹进行疲劳失效评定即可。针对3种压力工况，分别提取筒体螺纹最大应力点主应力，计算其当量交变应力强度幅，结果如下：①设备使用压力为0～140 MPa时，最大应力点处σ1=697.4 MPa、σ2=233.0 MPa、σ3=84.7 MPa，当量交变应力强度幅Seq=348.7 MPa。②设备使用压力为0～200 MPa时，最大应力点处σ1= 996.3 MPa、σ2=332.8 MPa、σ3=121.0 MPa，当量交变应力强度幅Seq=544.0 MPa。③设备使用压力为0～246.4 MPa时，最大应力点处σ1=1 225.5 MPa、σ2=409.4 MPa、σ3=148.8 MPa，当量交变应力强度幅Seq=602.3 MPa。

根据GB/T 34019—2017《超高压容器》，得到3种工况下的允许循环次数分别为N1=12 412次、N2=1 550次、N3=1 072次。

取0～140 MPa的预计循环次数为n1，0～200 MPa预计循环次数为n2，0～246.4 MPa预计循环次数n3=3(水压试验次数)次，则3种应力循环各自的使用系数为：

则累计使用系数应满足下式：

U=U1+U2+U3≤1.0

即设备循环次数应满足下列公式：

4 结语[12]

文中的超高压容器设计计算实例证明，依据GB/T 34019—2017《超高压容器》提供的指导能够完成超高压容器的设计计算。但详细计算过程的落实需要对标准有充分的理解，需要注意部分计算过程是交叉使用的，需要作循环计算。此外还需要注意，在ASME Ⅷ-3中，断裂力学评定是以FAD失效评定图为前提，而在GB/T 34019—2017《超高压容器》中只进行了断裂力学评定。希望GB/T 34019—2017的计算实例尽快出台，完善各种计算方法，使得超高压容器的设计计算更加合理，以方便广大压力容器设计工作者参考使用。