地铁异步电机间接定子量控制策略研究*

赵雷廷

(中国铁道科学研究院集团有限公司 机车车辆研究所， 北京 100094)

地铁牵引传动系统具有功率大、调速范围宽、启动转矩高等特点。由于受到开关损耗以及散热限制，系统牵引变流器开关频率通常设置较低，且采用分段同步调制技术[1]，因此，会在一定程度上影响电机矢量控制中电流调节的充分发挥。针对上述问题，在20世纪90年代业界提出了一种异步电机间接定子量控制策略[2-4](Indirect Stator-quantity Control,ISC)，其通过对定子磁链轨迹的跟踪实现转矩控制，不仅可以充分利用开关频率，减小峰值电流以及电机谐波损耗，而且还有效规避了直接转矩控制在低速范围内转矩脉动大、控制特性差的问题[5]。文章利用小信号分析法建立了ISC控制策略的近似线性化等效模型，进而推导出既考虑控制带宽又保证稳定裕度的电机转矩及定子磁链PI调节器的参数整定方法。

此外，由于地铁车辆运行过程中存在网侧电压波动、直流侧滤波电感和支撑电容参数受限制选取以及牵引变流器-异步电机系统在ISC控制策略下呈现的负阻抗特性等不利因素，系统直流侧电压、电流将很容易产生持续振荡，从而引起电机输出转矩脉动[6]。近年来，国内外众多学者针对上述问题已经展开了一定分析并提出了相应的解决措施[7-9]，将牵引变流器-异步电机系统简单等效为一个降低系统阻尼系数的恒定负阻抗[10]。本文则在上述理论基础上，将ISC近似线性化等效模型与直流侧输入滤波器模型相结合，建立了牵引传动系统综合线性化等效模型，从而将牵引变流器—异步电机系统等效为随系统工作点移动而实时变化的线性化输入导纳模型，继而展开系统稳定性分析，并提出了一种主动稳定控制器，有效的抑制了直流侧振荡现象，提高了系统的稳定性。

1 异步电机ISC控制策略

1.1 线性化等效模型建立

结合异步电机数学模型、牵引变流器脉宽调制模型最终建立ISC控制策略近似线性化等效模型。

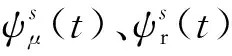
根据等效电路可以得到异步电机数学模型式(1)

(1)

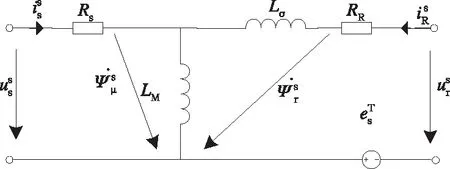
图1 异步电机 型等效电路

考虑到控制系统为获取电机定子电压、定子电流的基波分量，其A/D采样在当前开关周期中点进行，计算得到的开关时间在下一个开关周期起始处加载，因此，实际电机定子电压相对于控制系统给定的指令电压值将滞后半个开关周期，当忽略高频谐波且施加网侧电压波动补偿措施时牵引变流器脉宽调制策略线性化模型如式(2)

(2)

其中下标0表示对应变量的稳态值，A(t)为一个开关周期内求取变量平均值的函数，ωe则表示电机定子频率。

为补偿控制系统延时，ISC控制策略根据预测模型计算下一控制周期与当前控制周期的定子磁链空间矢量差值，从而得到下一控制周期的定子电压给定值，实现对异步电机转矩的控制。

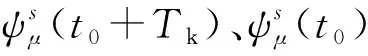
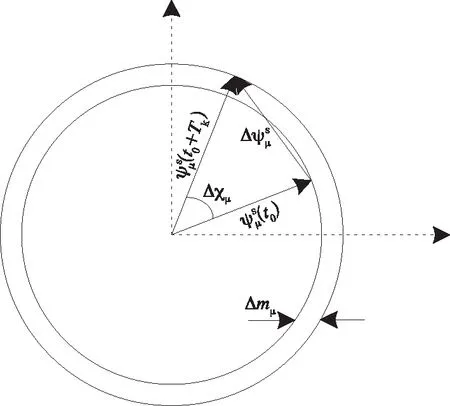
图2 定子磁链轨迹

因此可得到离散时间域下电机定子电压给定值为式(3)

Rsis(t0+Td)

(3)

为建立ISC控制策略近似线性化等效模型，在连续时间域下定义控制系统给定电机定子电压如式(4)所示

(4)

其中

(5)

定义变量如式(6)

(6)

则将式(4)和式(5)在系统工作点附近分别线性化，可以得到

usref(t)=KvTcucl(t)+KvTψψμ(t)+Ksis(t)

(7)

ucl=uc+Fωωm(t)+Fmrmr(t)

(8)

其中

uc=F(yref(t)-Ay(t))+Ffωyref(t)

(9)

(10)

(11)

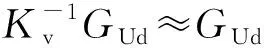
us(t)=KvTcuc(t)+KvTψψμ(t)+Ksis(t)+

KvTcFmrmr+KvTcFωωm(t)-AGUdUd(t)

(12)

y(t)=DPuc(t)+Q(1-DA)GUdUd(t)+

(1-D)ωm(t)

(13)

其中

(14)

Q(s)=

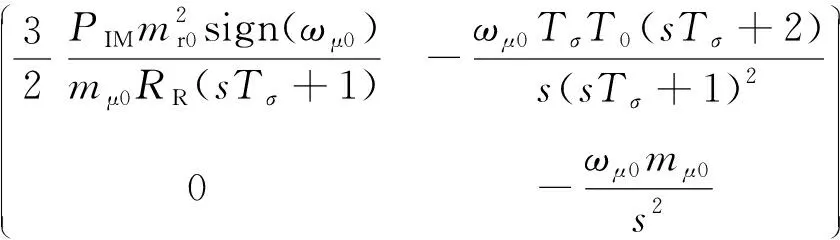
(15)

(16)

根据得到的近似线性化等效模型建立ISC控制闭环系统框图如图3所示。

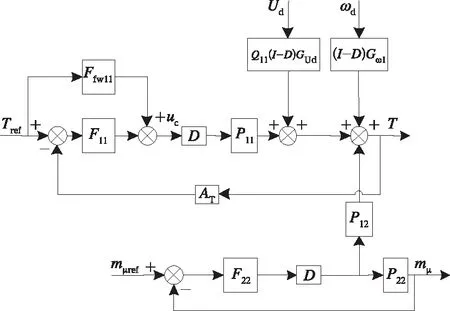
图3 ISC控制闭环系统框图

1.2 PI调节器参数整定

为完善ISC控制策略近似线性化等效模型，则需要针对电机输出转矩以及定子磁链PI调节器的参数进行合理的整定。从图3可以看出电机转矩和定子磁链控制实现了近似解耦，继而得到电机转矩控制系统闭环传递函数如式(17)～式(19)所示。

(17)

引入新的传递函数

(18)

≈e-Td·s×e-Td·s=e-Tk·s

(19)

则系统开环传递函数可近似表示为

(20)

为使电机转矩闭环控制系统具有较大的相角稳定裕度，开环传递函数在其穿越频率ωc附近应保持-20 db/dec的斜率，即一阶微分环节的交接频率应尽可能的小于穿越频率。

(21)

因此可以得到开环传递函数获得目标穿越频率ωcd时系统转矩PI调节器比例参数的表达式

KPI=Tσωcd-1

(22)

结合式(21)得到积分参数的限制函数

(23)

一般积分参数选取限制值的1/4时，系统具有良好的动态响应而且稳态误差较小

(24)

系统相角稳定裕度公式如下所示

(25)

可以看出其第一项近似为76.3°，而第二项则与系统延时以及穿越频率的大小相关，因此为保证一定的目标稳定裕度φmd，目标穿越频率限制函数如式(26)所示

(26)

电机定子磁链控制系统闭环传递函数亦可从图3中得到式(27)

(27)

同理推导出其开环传递函数获得目标穿越频率ωμcd时定子磁链PI调节器比例参数的表达式(28)

(28)

其相角稳定裕度公式为式(29)

(29)

因此为保证一定的目标稳定裕度φμmd，目标穿越频率限制函数如式(30)所示

(30)

2 基于ISC控制策略的系统稳定性分析

图4(a)所示为地铁牵引传动系统框图，R为线路电阻与电感内阻之和、L为滤波电感，C为支撑电容。如果将直流网侧电压E(t)与直流侧电流id(t)作为牵引传动系统的输入，直流侧电压Ud(t)作为系统输出，则系统输入滤波器频域下方程为式(31)

(31)

同时定义牵引变流器—异步电机系统等效输入导纳线性化模型为式(32)

(32)

因此可以得到如图4(b)所示的牵引传动系统线性化结构图。

图4 地铁牵引传动系统框图

继而将牵引传动系统整体稳定性的分析归结于对系统开环传递函数YZDC的分析。

将ISC控制策略近似线性化等效模型与地铁牵引传动系统直流侧滤波器模型相结合，最终可以将牵引变流器—异步电机系统等效为随系统工作点移动而变化的输入导纳线性化模型如图5所示。

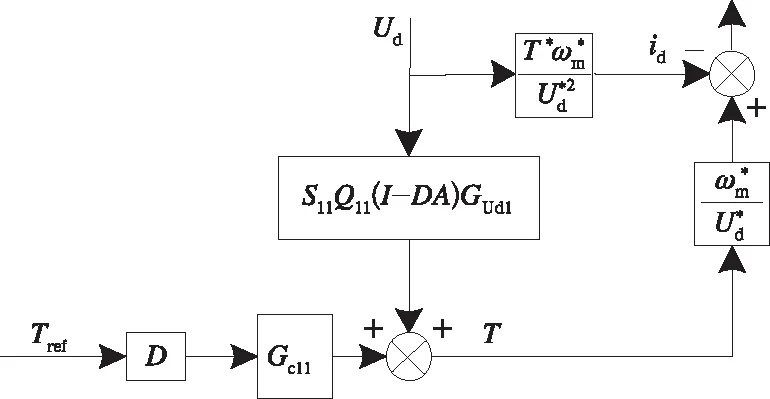
图5 输入导纳线性化模型

根据图5推导出其精确表达式为

(33)

Gc11=

(34)

如图(6)所示为系统在直流侧电压1 500 V，滤波电感5.2 mH，支撑电容8.6 mF，线路电阻与电感内阻之和34.8 mΩ，电机等效漏感2 mH的条件下开环传递函数YZDC频率域稳定分析仿真结果，在幅频特性曲线大于0的频率范围之内相频特性曲线穿越180°一次，根据奈奎斯特对数频率稳定判据可知此时系统处于不稳定状态，整个系统将产生持续振荡。

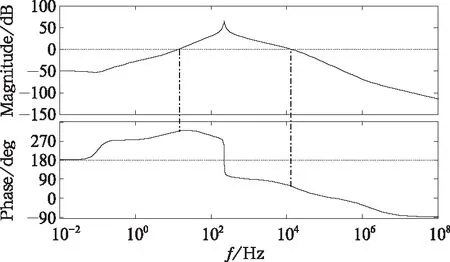
图6 开环传递函数YZDC伯德图

因此如何获得理想的牵引变流器—异步电机等效输入导纳线性化模型，从而改善系统开环传递函数幅频、相频特性成为了系统稳定性设计的关键。

3 主动稳定控制器设计

通过设计主动稳定控制器在线修正电机输出转矩分量给定值，以获得最终的理想牵引变流器—异步电机等效输入导纳线性化模型，修正公式如式(35)所示

(35)

其中Kst为主动稳定控制器，B为带通滤波器。传递函数ZDC由于滤波电感以及支撑电容参数受限制选取导致阻尼系数较小，因此在谐振频率ω0附近其对数幅频曲线有较大的尖峰，同时相角从90°突变至-90°，如果此时线性化输入导纳Y等效为复频域下一向量，当Re{Y(ω0)}<0时，arg(YZDC(ω))必然穿越(2k+1)180°(k=0、±1、±2…)从而导致系统处于不稳定状态。设计的主动稳定控制器分为两个部分，其中Kω和KT分别用于稳定当前等效输入导纳线性化模型即式(33)中的第1项Y1和第2项Y2。

采用主动稳定控制器后理想的牵引变流器—异步电机等效输入导纳线性化模型如式(36)所示

(36)

根据式(33)和式(36)可以得到系统在惰性情况下即T0=0且KT=0时，理想输入导纳为

(37)

其中

(38)

因此可以得到

(39)

为抑制系统振荡，提高稳定性，则需要理想的等效输入导纳在复频域下相角始终处于90°～-90°之间，至少在输入滤波器谐振频率附近满足上述条件，继而可以得到限制条件为

(40)

选取两倍的限制值可以得到主动稳定控制器Kω分量的表达式

(41)

同理为保证系统工作在牵引或者制动的工况下仍然处于稳定状态则还应满足如式(42)要求

(42)

根据式(42)可以看出系统只有工作在带宽频率段且为牵引工况时才需要稳定系数KT，因此设计KT如式(43)所示

(43)

结合式(41)推导出主动稳定控制器精确模型为

(44)

ISC控制策略采用主动稳定控制器之后的整体系统开环传递函数伯德图如图7所示，与图6相比，在同一工作点下其幅频特性曲线大于0的频率范围之内相频特性曲线没有穿越(2k+1)180°，从而使得系统处于稳定状态。

4 仿真验证

如图8所示为基于主动稳定控制器的异步电机ISC控制策略系统结构框图，利用定子磁链规划最优效率控制模块获得当前负载下能使异步电机效率达到最优的定子磁链给定值；通过采用主动稳定控制器得到电机输出转矩给定值，从而抑制直流侧振荡，提高系统稳定性；结合预测模型计算结果，最终给出牵引变流器开关时间，驱动异步电机正常运行。

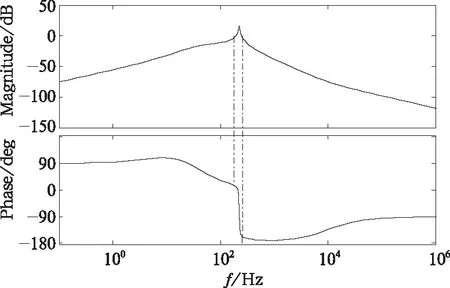
图7 理想线性化导纳下的开环传递函数伯德图

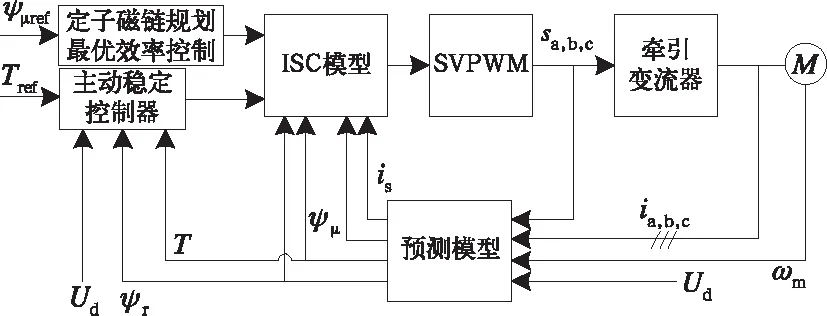
图8 间接定子量控制策略结构

基于上述控制策略利用Matlab进行系统仿真，图9所示为电机转矩(标幺值)以及定子磁链(交、直轴分量与合成矢量比值)波形，其具有良好的动态响应和微小的稳态误差。

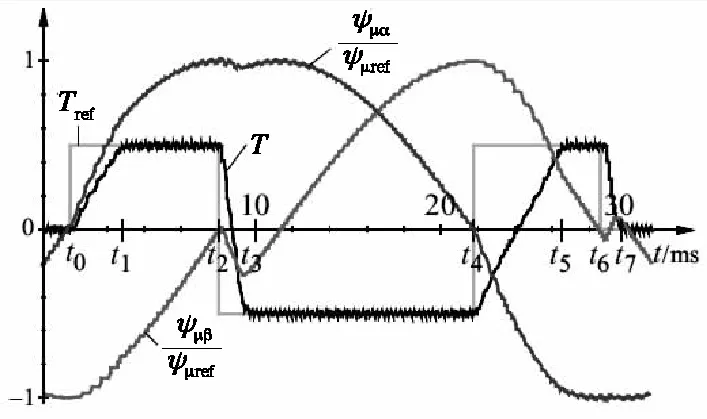
图9 电机转矩及定子磁链波形

图10给出了未采用主动稳定控制器与采用主动稳定控制器两种情况下，地铁牵引传动系统主要变量的仿真波形对比。

可以看出系统采用基于主动稳定控制器的ISC控制策略之后如图10(b)所示，在转速从0上升至3 300 r/min，运行工况由牵引→惰性→制动的过程中，消除了之前未采用主动稳定控制器时如图10(a)所示的系统振荡现象，其直流侧电压Ud、网侧直流电流ig以及电机输出转矩T变化平稳。

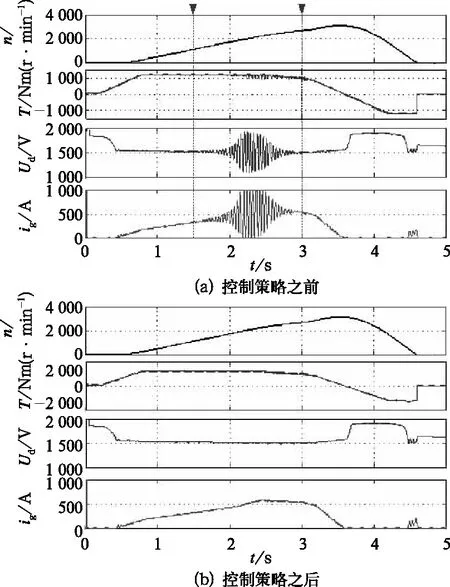
图10 牵引传动系统运行仿真图

5 结 论

利用小信号分析法，分别建立了系统在某一工作点的异步电机数学模型、牵引变流器脉宽调制等效模型从而得到ISC控制策略的近似线性化等效模型，推导出同时考虑系统控制带宽以及稳定裕度的电机转矩、定子磁链PI调节器参数整定方法。结合地铁牵引传动系统直流侧滤波器等效模型，将牵引变流器—异步电机系统等效为输入导纳线性化模型，继而利用奈奎斯特对数频率稳定判据阐释了直流侧振荡的机理，并在此基础上提出了基于主动稳定控制器的ISC控制策略，通过在线修正电机输出转矩给定值成功解决了地铁牵引传动系统振荡的问题，确保了地铁车辆的安全稳定运行。