层间连接对CRTS l型板式无砟轨道-路基系统力学特性的影响研究

雷鹏飞

（中铁磁浮交通投资建设有限公司，武汉430060）

1 概述

无砟轨道由于具有使用寿命长、高平顺性、少维修等特点，在国内外高速铁路中得到了广泛的应用。从20世纪60年代起，日本、德国等发达国家对无砟轨道进行了深入的研究，逐步形成了拥有各自特色的无砟轨道结构形式。

我国在吸收日本新干线单元板式无砟轨道的基础上，针对我国铁路的运营条件和地域条件研发了CRTS I型板式无砟轨道，并成功应用于哈大、沪宁城际、广珠、广深港等多条客运专线[1]。

自CRTS I型板式无砟轨道在我国得到成功应用，国内外学者针对其静力、动力特性进行了大量研究，取得了丰硕的研究成果。

2 CRTS l型板式无砟轨道-路基空间力学模型

在ANSYS环境下生成的CRTS I型板式无砟轨道-路基力学模型总体图及大样图分别如图1和图2所示。

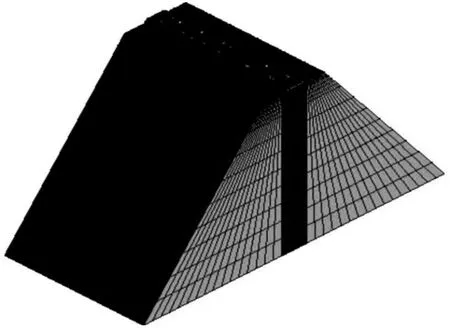
图1 CRTS l型板式无砟轨道-路基力学模型总体图

图2 CRTS l型板式无砟轨道-路基力学模型大样图

模型中，钢轨用beam4梁单元模拟，轨道板、CA砂浆、底座、基床表层、基床底层、地基以solid45实体单元模拟。

钢轨与轨道板之间的连接采用combin14弹簧—阻尼单元模拟，为考虑扣件的尺寸效应，避免将钢轨与轨道板对应节点直接相连造成轨道板的应力集中，将每个钢轨节点与其对应扣件尺寸范围内的轨道板节点均相连。

轨道板与CA砂浆、底座与路基间连接采用松散连接、紧密连接以及接触单元连接3种不同的连接方式。松散连接假定无砟轨道层间无摩擦，层与层仅垂向连接，本文采用combin14弹簧-阻尼单元对此加以模拟[2]；紧密连接假定无砟轨道层间摩擦系数无穷大，不同层之间变形协调一致，本文不同层间采用共节点对此加以模拟；接触单元连接可以考虑层间摩擦以及层间分离脱空，本文采用contact178单元对此加以模拟。

3 模型验证

采用遂渝线动力测试结果对上述层间接触单元连接空间力学模型进行验证。模型计算参数见表1。不同速度级别下路基上CRTS I型板式无砟轨道地段的货车轮轨垂向力平均值最大为131.2 kN，本文轮载取131.2 kN。

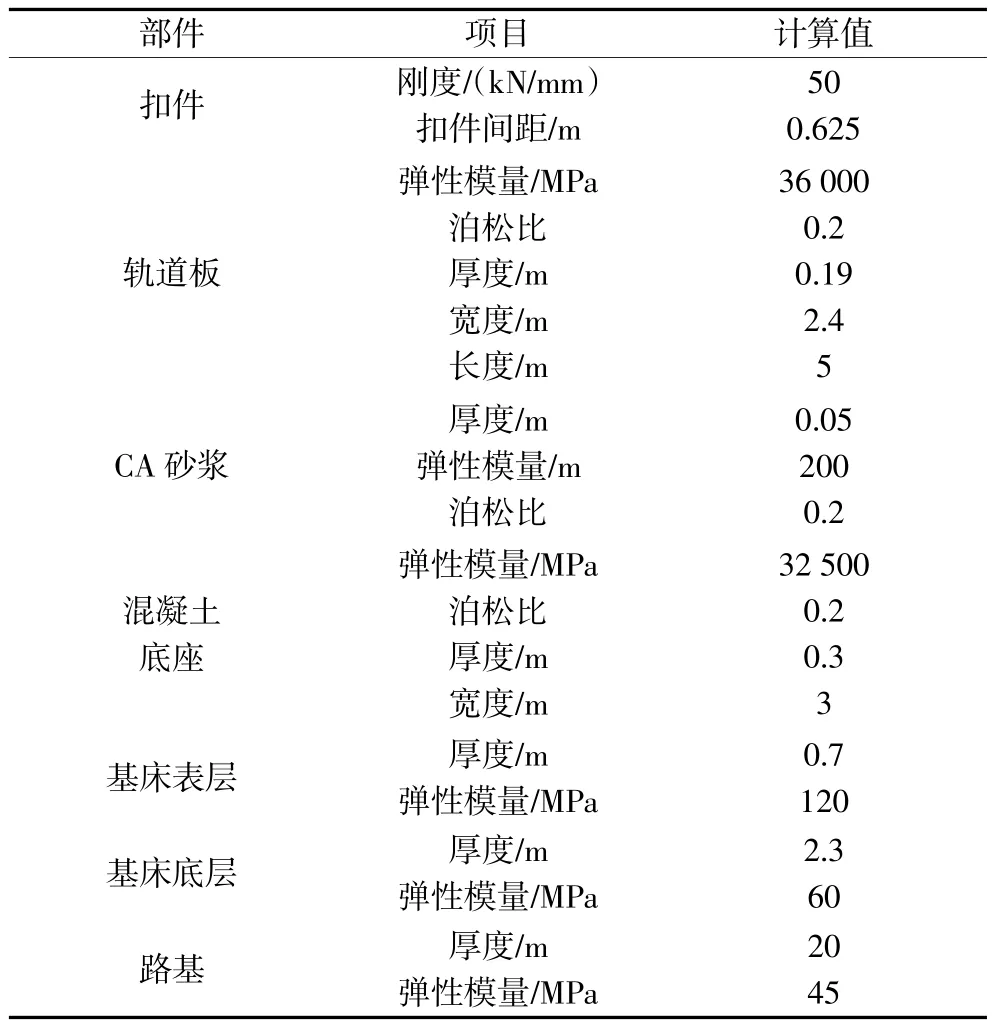
表1 轨道和路基计算参数

本文层间接触单元连接模型计算结果及遂渝线实测值比较见表2。

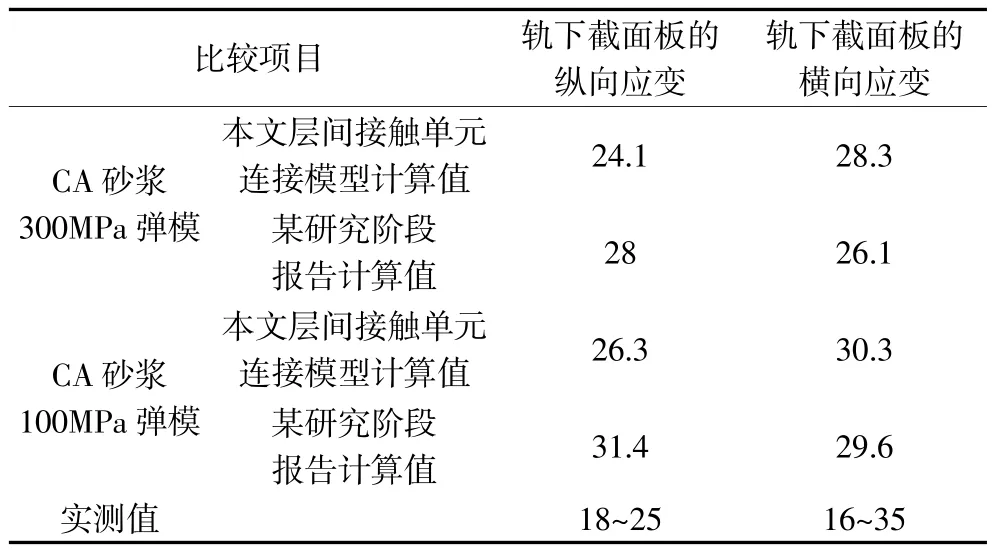
表2 遂渝线板式无砟轨道计算结果比较表

表2数据表明，本文层间接触单元连接力学模型能够反映无砟轨道受力的实际情况。

4 仿真计算

4.1 计算参数及计算工况

路基上CRTS I型板式无砟轨道力学模型中轨道和路基主要计算参数如表1所示。

本文列车荷载取为100kN，并考虑3.0的动载系数，以300kN动荷载单轮对移动加载，路基不均匀沉降采用余弦型，20m范围内最大沉降15mm，温度梯度荷载考虑无砟轨道上热下冷，取10℃。

为研究不同荷载作用下无砟轨道-下部基础层间连接对路基上CRTS I型板式无砟轨道各部件的影响，设置8种工况，如表3所示。

表3 计算工况

4.2 计算结果及分析

4.2.1 列车荷载工况下计算结果及分析

表4给出了在列车荷载作用下，无砟轨道-下部基础3种不同层间连接对轨道板以及底座板的影响规律。

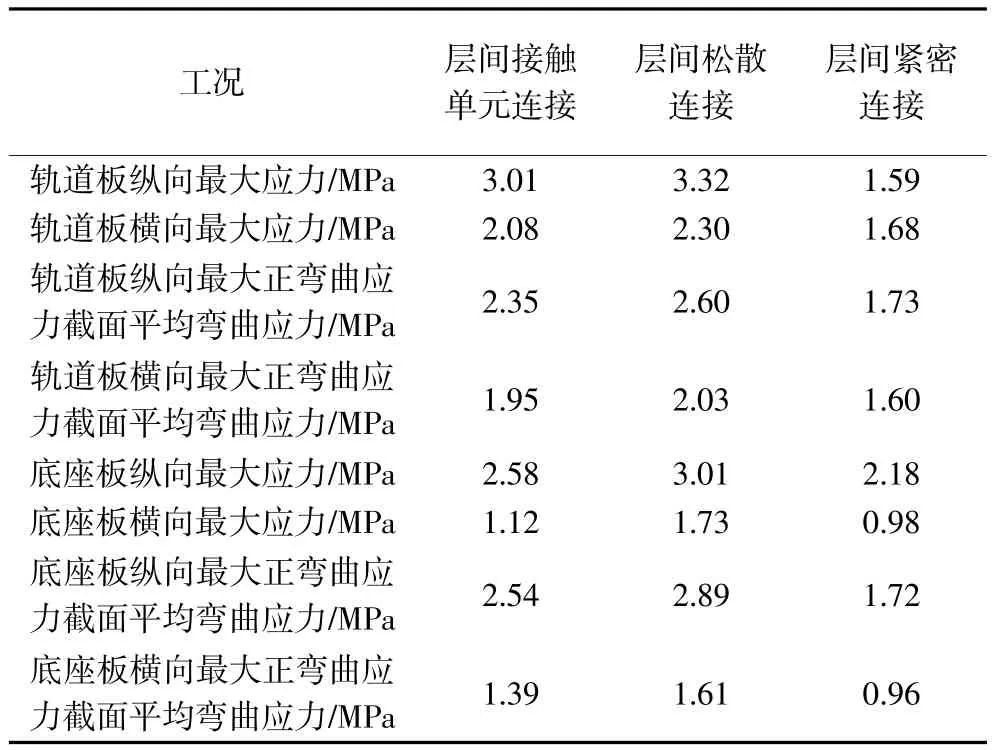
表4 列车荷载下不同层间连接对轨道板及底座板应力影响结果比较表

从表4可以看出，在列车荷载的作用下，不同层间连接下轨道板及底座板应力计算结果有不同程度的差别。对于轨道板，层间松散连接力学模型下轨道板纵向最大应力、横向最大应力、纵向最大正弯曲应力截面平均弯曲应力、横向最大正弯曲应力截面平均弯曲应力分别比层间接触单元连接力学模型大10.3%、10.6%、10.6%、4.1%。层间紧密连接力学模型下轨道板纵向最大应力、横向最大应力、纵向最大正弯曲应力截面平均弯曲应力、横向最大正弯曲应力截面平均弯曲应力分别比层间接触单元力学模型小47.2%、19.2%、26.4%、17.9%。对于底座板，层间松散连接力学模型下底座板纵向最大应力、横向最大应力、纵向最大正弯曲应力截面平均弯曲应力、横向最大正弯曲应力截面平均弯曲应力分别比层间接触单元连接力学模型大16.7%、54.5%、13.8%、15.8%。层间紧密连接力学模型下底座板纵向最大应力、横向最大应力、纵向最大正弯曲应力截面平均弯曲应力、横向最大正弯曲应力截面平均弯曲应力分别比层间接触单元连接力学模型小13.5%、12.5%、32.9%、30.9%。

进一步分析，可以得到以下规律：在列车荷载作用下，层间松散连接力学模型下轨道板及底座板应力最大，层间紧密连接力学模型下轨道板及底座板应力最小，层间接触单元连接力学模型下轨道板及底座板应力介于二者之间。造成上述规律的主要原因是：不同层间连接力学模型下无砟轨道抗弯刚度不同，层间松散连接下无砟轨道抗弯刚度最小，层间紧密连接下无砟轨道抗弯刚度最大，层间接触单元连接下无砟轨道抗弯刚度介于二者之间。而无砟轨道抗弯刚度越大，其弯曲应力越小[3]。

4.2.2 路基不均匀沉降荷载工况下计算结果及分析

路基不均匀沉降作用下，2种不同层间连接对轨道板以及底座板的影响规律见表5。

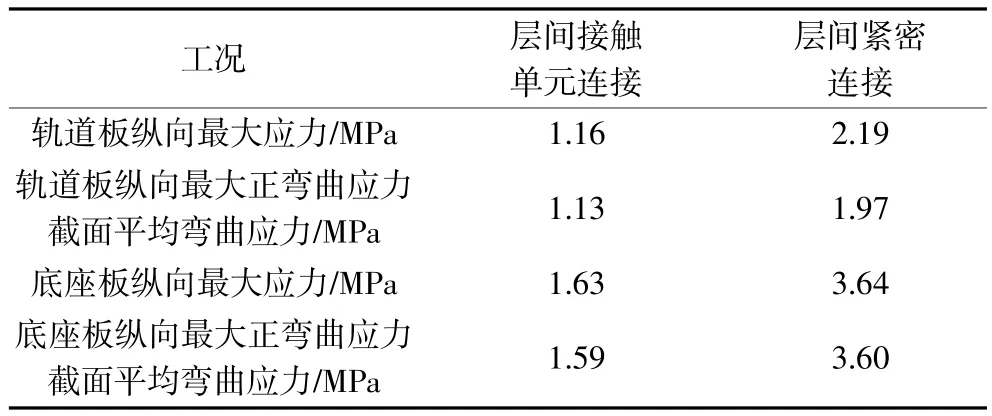
表5 路基不均匀沉降荷载下不同层间连接对轨道板及底座板应力影响结果比较表

由表5可知，路基不均匀沉降作用下，不同层间连接力学模型下轨道板以及底座板纵向应力计算结果均有显著差别。

层间紧密连接力学模型下轨道板纵向最大应力、纵向最大正弯曲应力截面平均弯曲应力分别比接触单元连接力学模型大88.8%、74.3%。层间紧密连接力学模型下底座板纵向最大应力、纵向最大正弯曲应力截面平均弯曲应力分别比接触单元连接力学模型大123.3%、126.4%。

造成上述现象的原因主要是：在不均匀沉降荷载工况下，无砟轨道各部件之间存在局部脱空，接触单元模型可以考虑局部脱空对无砟轨道受力的影响，无砟轨道变形和受力均减小，而层间紧密连接下无砟轨道和下部基础变形是一致的，其变形和受力较大[4,5]。

4.2.3 温度梯度荷载工况下计算结果及分析

温度梯度荷载作用下，3种层间连接对轨道板的影响规律见表6。

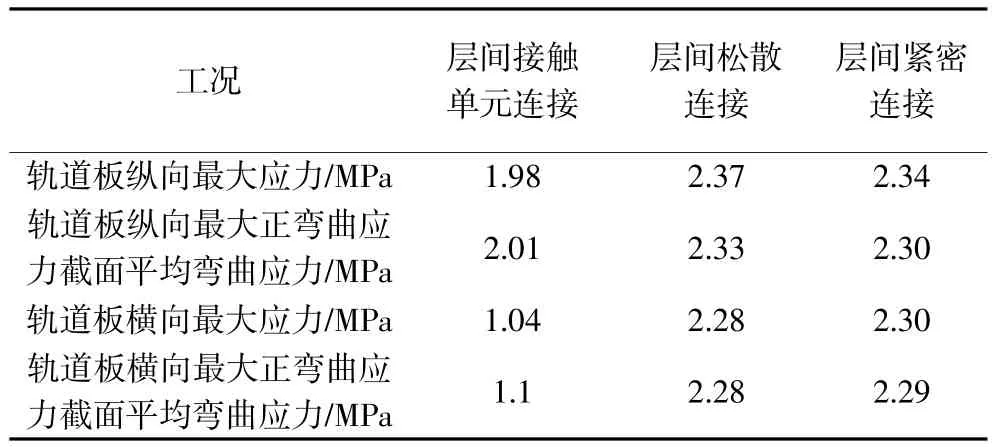
表6 温度梯度荷载下不同层间连接对轨道板受力影响结果比较表

表6表明，温度梯度荷载下，不同层间连接力学模型下轨道板纵向应力计算结果有一定的差别，不同层间连接力学模型下轨道板横向应力计算结果差别显著。

层间紧密连接力学模型下轨道板纵向最大应力、纵向最大正弯曲应力截面平均弯曲应力、轨横向最大应力、横向最大正弯曲应力截面平均弯曲应力分别比接触单元连接力学模型大19.7%、15.9%、119.2%、107.3%。层间松散连接力学模型下轨道板纵向最大应力、纵向最大正弯曲应力截面平均弯曲应力、横向最大应力、横向最大正弯曲应力截面平均弯曲应力分别比接触单元连接力学模型大 18.2%、15.4%、121.2%、108.2%。

造成上述现象的原因主要是：接触单元力学模型考虑了在温度梯度荷载作用下局部脱空效应对无砟轨道受力的影响，而紧密连接及松散连接力学模型都没有考虑这种影响。

5 结论

本文考虑无砟轨道-下部基础不同层间连接，建立了CRTS I型板式无砟轨道-路基空间力学模型，并探讨了在列车荷载、路基不均匀沉降荷载、温度梯度荷载作用下，不同层间连接对轨道板及底座板力学特性的影响规律，主要研究结论如下：

1）列车荷载作用下，无砟轨道-下部基础不同层间连接力学模型下轨道板及底座板应力计算结果有不同程度的差别。层间松散连接力学模型下轨道板及底座板应力比接触单元连接力学模型大4.1%～54.5%，层间紧密连接力学模型下轨道板及底座板应力比接触单元连接力学模型小12.5%～32.3%。

2）路基不均匀沉降荷载作用下，无砟轨道-下部基础不同层间连接力学模型下轨道板及底座板纵向应力计算结果差别显著[6]。层间紧密连接力学模型下轨道板纵向应力比接触单元连接力学模型下大74.3%～88.8%，底座板纵向应力比接触单元连接力学模型大123.3%～126.4%。

3）温度梯度荷载作用下，无砟轨道-下部基础不同层间连接下轨道板纵向应力计算结果有一定的差别，轨道板横向应力计算结果差别显著。层间紧密连接及松散连接力学模型下轨道板纵向应力比层间接触单元连接力学模型大15.4%～19.7%，层间紧密连接及松散连接力学模型下轨道板横向应力比层间接触单元连接力学模型大107.3%～121.2%。

4）为了更好地反映无砟轨道的空间力学特性，有必要在力学模型中使用层间接触单元，以提高计算精度。