浅谈平面直角坐标系内三角形的坐标面积公式的推导及应用
2019-01-28云南省昆明市宜良县第二中学李春红
云南省昆明市宜良县第二中学 李春红
初中阶段求三角形面积的方法有很多,常见的有直接计算法与割补法.本文在此基础上总结出一种利用坐标计算三角形面积的方法,对涉及平面直角坐标系中三角形面积问题时,用这种方法计算能省时省力.
一、平面直角坐标系内三角形的坐标面积公式的推导
例1,如图,三角形ABC的三个顶点的坐标分别为A(xA,yA)、B(xB,yB)、C(xC,yC),求S△ABC.
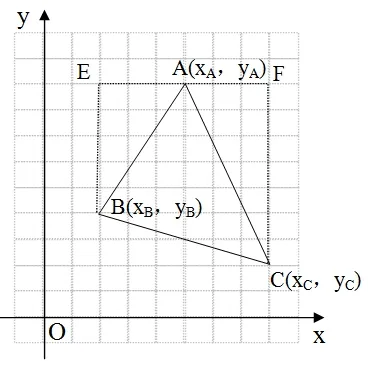
解:过点A 作EF∥x轴,分别过点B、C作y轴的平行线交直线EF于点E、F,
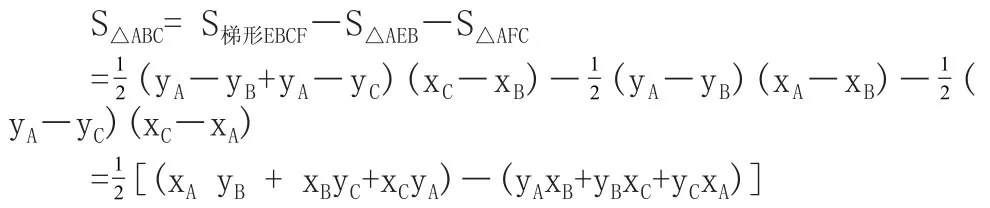
把上式中的xAyB、xByC、 xCyA、yAxB、 yBxC、yCxA分别记为①、②、③、④、⑤、⑥,则三角形ABC的面积公式可以表示为:

如果把三角形ABC的三个顶点的坐标按逆时针排序如下:
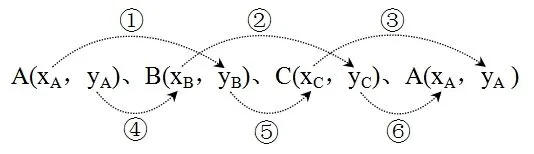
则公式S△ABC=[(①+②+③)-(④+⑤+⑥)]可以描述为:三角形三个顶点的坐标逆时针排序一周,则这个三角形的面积等于“大跨度积之和”与“小跨度积之和”之差除以2.
如果把三角形ABC的三个顶点的坐标按顺时针排序如下:
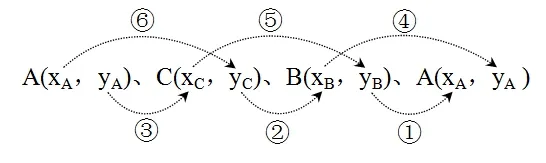
二、三角形坐标面积公式的应用
(一) 求定点三角形的面积
例2,已知,三角形三个顶点的坐标分别为A(-2,3)、B(6,-1) 、C(4,5),求S△ABC.
解法一(点的坐标逆时针排序一周):
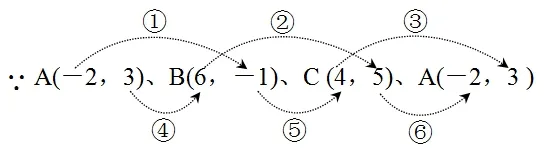
△ABC公式)
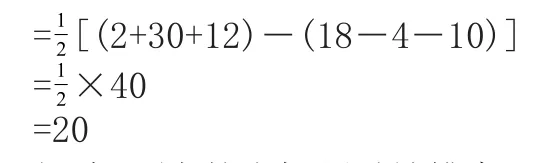
解法二(点的坐标顺时针排序一周):
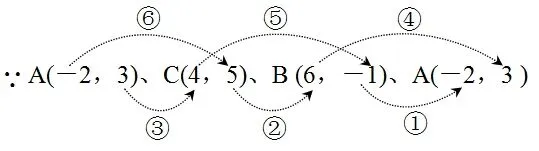
∴S=-1[(⑥+⑤+④)-(③+②+①)](三角形坐标面
△ABC2积公式)
=-12[(-10-4+18)-(12+30+2)]
=-12×(-40)
=20
(二) 求动点三角形的面积
例3,如图,在直角坐标系中,直线AB与抛物线y=x2+x的交点A、B的坐标为A (-1,0)、B(1,2).
(1)在抛物线上是否存在点Q (x,y),且-1<x<1,使S△ABQ最大?若存在,求出点Q的坐标和S△ABQ的最大值;若不存在,请说明理由.
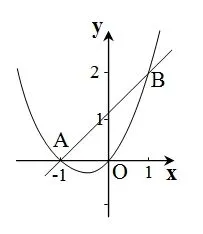
(2)在抛物线上是否存在点P,使S△ABP=2?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)结论:存在.
理由:∵点Q的坐标为(x,y),且在抛物线上,
∴Q点的纵坐标y=x2+x,
△ABQ三个顶点的坐标逆时针排序一周如下:
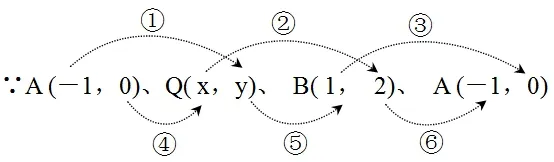
△ABQ积公式)
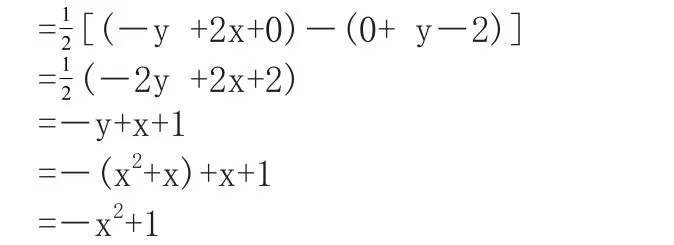
∴满足条件的点Q的坐标为(0,0),S△ABQ的最大值为1.
(2)结论:存在.
理由:设点P的坐标为(x,y),且在抛物线上,
∴P点的纵坐标y=x2+x,
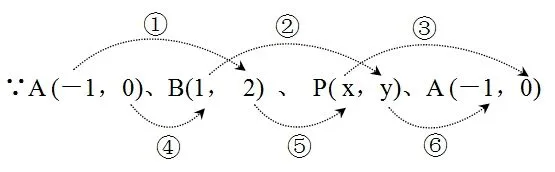
以上△ABP三个顶点的坐标排序可能是逆时针(x<-1或x>1),也可能是顺时针(-1< x<1),
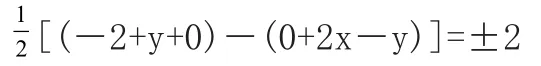
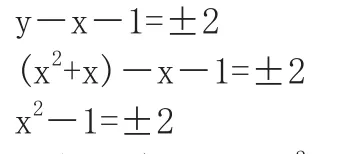
可得两个方程:x2=3,x2=-1(无解),
解x2=3,得x1=-,x2=,从而可得y1=3-,y2=3+.
∴满足条件的点P的坐标有两个点P1(-,3-)、P2(,3+).
总之,三角形的面积用坐标的形式公式化以后,可为学生提供解决定点简单问题和动点复杂问题的通法,对解决实际问题起到事半功倍的作用.
