心电信号预处理方法研究

2019-01-28王旭钱伟余宇帆

中国医学工程 2018年12期

王旭，钱伟，余宇帆

（广东环境保护工程职业学院环境监测系，广东佛山 528216）

心电信号是一种微弱的生理信号，是人体机能的客观表现，能够准确地反应人体健康状况。但是由于心电信号的幅度小，给信号采集带来很大的挑战，而且在进行心电信号采集过程中，会受到工频干扰、基线漂移及肌电噪声等干扰，给临床医学诊断造成极大的困难。

在传统的基线漂移去除方法中，主要采用样条插值，多项式拟合估计基线漂移，从而消除估计的噪声[1]，有学者在此基础上，提出一种改进的心电信号滤波算法，能适应更宽范围的基线噪声频率分布[2]，此算法实现复杂，算法效率低。采用经验模态分解的方法，选择最优EMD分解层数改进基线漂移的去除方法[3]，有学者在此基础上，根据变分模态分解理论，去除心电信号中的含有基线漂移成分的模态分量，有效去除基线漂移干扰[4]，该方法效果良好，但需要通过先验估计计算最优层数，且临床实用性有待一步验证。通过数据延时的方法实现基于零相位滤波器的实时改进，从而抑制基线漂移[5]，该方法滤波效果良好，但不能满足实时性要求。将小波变换与自适应滤波器结合起来，消除心电信号中的基线漂移[6]，该方法容易受到参考信号的影响，鲁棒性较差，有学者在此基础上进行改进，提出无模型自适应控制的心电基线漂移抑制方法[7]，实用性强，具有极其重要的使用价值和临床意义，缺点是期望输入模型需要多次计算，复杂度高，计算效率较慢。

在去除工频干扰的研究中，有学者通过对比平滑滤波、中值滤波、FIR滤波及小波变换对同一心电信号中的工频干扰滤波效果，证明小波变换在抑制心电信号的工频干扰具有较大优势[8]。史国华等[9]提出基于模板的方法滤除心电信号中的工频干扰，实现简单，复杂度低，但容易受到其他噪声的干扰，且具有不确定性。郝东昊等[10]提出抑制心电信号中工频干扰的方法，应用数字硬件技术，设计高衰减倍数的滤波采样系统，其优点是处理速度快，但硬件系统会带来其他干扰和噪声。

1 工频干扰与基线漂移

在心电信号采集过程中，常伴有工频干扰和基线漂移，工频干扰甚至会淹没胎儿心电信号，基线漂移则在心电信号中以正弦波形式出现，导致临床医生无法准确地判断胎儿心电波形所具有的生理信息，见图1。

图1 含有基线漂移和工频干扰的心电信号

在硬件上虽然可以设计滤波电路过滤工频干扰，但不能完全解决问题，而数字滤波器具有简单易实现等特点，且能较好地滤除工频干扰和基线漂移。本文根据零极点分布对系统频率响应特性的影响规律，设计消除工频干扰和基线漂移的数字陷波器，该方法能较好地消除心电信号中的工频干扰，且实现简单。本文在此基础上设计一种梳状滤波器消除0 Hz处基线漂移和50 Hz及其倍频工频干扰。

2 梳状滤波器设计

梳状滤波器可以在保持信号带宽不变的情况下消除谐波干扰，将频率响应设计为周期性的，使其在0 Hz、50 Hz及其高次谐波处有很窄的阻带，这样就可以消除0 Hz处的基线漂移和50 Hz及其高次谐波的工频干扰。

梳状滤波器的输入信号形式可表示为：

式（2.1）中x(n)是期望得到的滤除干扰之后的信号，Bksink (ωcn +ϕk)是基频为 0 Hz和 50 Hz及其谐波干扰信号。梳状滤波器的频率响应是ω的周期函数，周期是2π/L，其中L是一个正整数。若H（Z）是一种有单个通带或阻带的滤波器，则梳状滤波器可以通过用L个延时单元代替它的每个延时而产生，则梳状滤波器的传输函数结构为：

已知IIR梳状滤波器传输函数为：

根据式（2.3）进行梳状滤波器的设计，令z=ejω，带入上式得到：

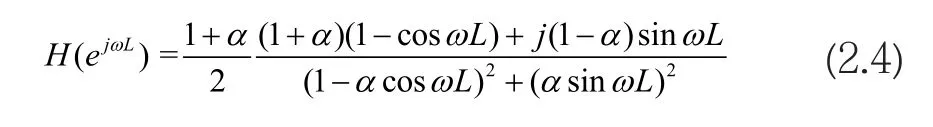
对式（2.4）求幅值，有：

给出阻带波纹计算公式：

要求最小阻带衰减αs=40 dB，由上式得出δs=0.01，即|H(ejωL)|=δs=0.01；要求最小阻带衰减αs=24 dB，由上式得出δs=0.06，即|H(ejωL)|=δs=0.06。

上式中阶数L的计算公式如下所示：

式（2.7）中fz为采样率，ωc为陷波频率。

医院临床心电数据的采样率为fz1=500 Hz，需要滤掉0 Hz处基线漂移和50 Hz及其谐波产生的干扰，故陷波频率为ωc=50 Hz，L=fz/ωc=10，代入|H(ejωL)|=0.01中，得到α=0.8568，代入上式中，得到梳状滤波器的传输函数：

式（2.8）幅频响应曲线如图2所示。

图2 应用于医院临床心电信号的梳状滤波器幅频响应曲线

MIT-BIT心电数据库中采样率为fz2=1 000 Hz，需要滤掉0 Hz处基线漂移和60 Hz及其谐波产生的干扰，故陷波频率为ωc=60 Hz，L=fz/ωc=17，由于阶数L为整数，实际消除62 Hz及其谐波造成的干扰，代入|H(ejωL)|=0.06中，得到α=0.9068，代入上式中，得到梳状滤波器的传输函数：

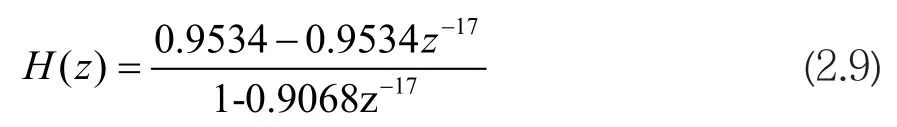
式（2.9）幅频响应曲线如图3所示。

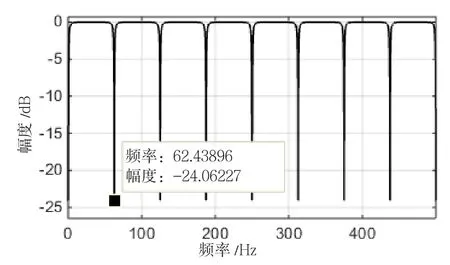
图3 应用于MIT-BIT心电信号的梳状滤波器幅频响应曲线

3 心电信号低通滤波

一般成人心电信号频率主要位于0.05～100.00 Hz，大部分能量位于0.5～50.0 Hz，胎儿心电信号的频率位于0.05～200.00 Hz，大部分能量位于14～160 Hz，因此设计一个低通滤波器滤除频率大于200 Hz的信号，其传输函数为：

式（3.1）中，α=(1-sinωc)/cosωc，ωc为3 dB的截止频率。已知心电信号的采样率为fs=1 000 Hz，应用低通滤波器去除频率大于200 Hz噪声成分，设置3 dB的截止频率ωc=180 Hz，则低通滤波器的传输函数为：

式（3.2）幅频响应曲线如图4所示。

图4 低通滤波器幅频响应曲线

4 仿真实验与结果分析

基于傅里叶级数变换的心电信号合成方法在MATLAB 2014b上编程实现，在Windows 7环境中运行。

4.1 合成信号仿真测试

设定采样率fs=500 Hz，在MATLAB上模拟产生母体心电信号和胎儿心电信号，再进行叠加，加入高斯白噪声、50 Hz频率的工频干扰、0.06 Hz频率的基线漂移干扰，运用上式梳状滤波器进行滤波，从时域和频域分别显示梳状滤波效果。时域效果如图5所示。

图5 梳状滤波时域效果图

频域效果如图6所示。

图6 梳状滤波频域效果图

从图中分析：在时域中，心电信号得到完好的滤波效果，去除大部分的工频干扰与基线漂移；在频域中，位于0 Hz和50 Hz的幅度得到较大的抑制，说明滤波效果良好。

4.2 临床信号仿真测试

采用本文中的信号预处理算法，分别对MITBIT心电数据库和国内临床心电数据做算法仿真测试，实验结果如图7～10所示。

图7 MIT-BIT心电数据库时域滤波效果图

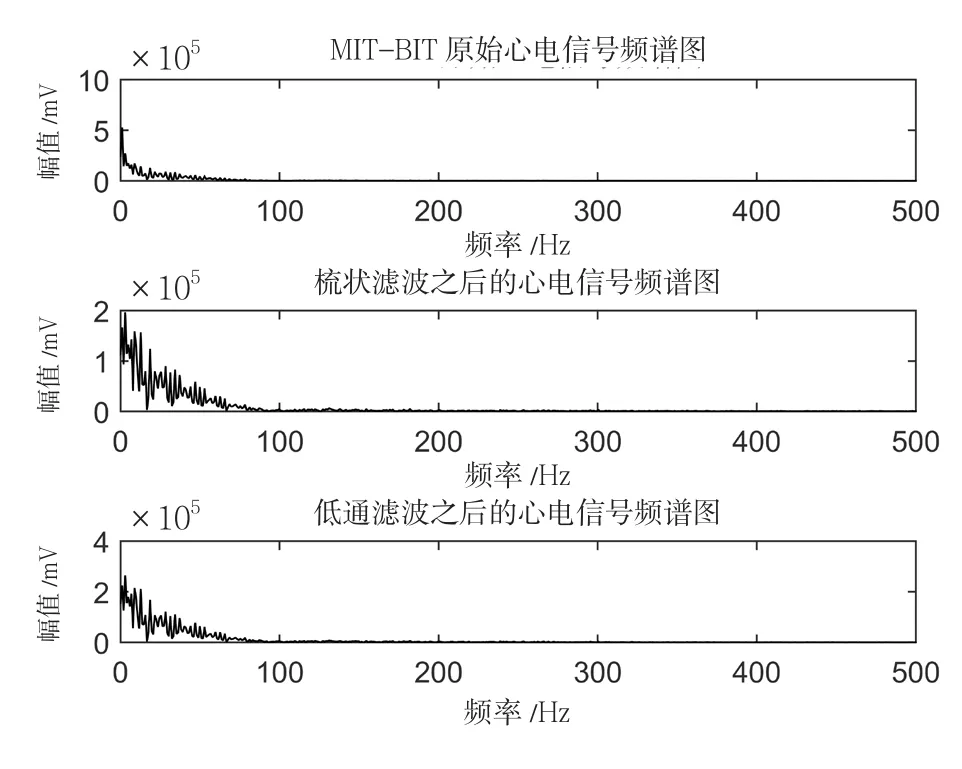
图8 MIT-BIT心电数据库频域滤波效果图

图9 国内临床心电数据库时域滤波效果图

图10 国内临床心电数据库频域滤波效果图

从图中分析：在MIT-BIT心电数据中，基线漂移和工频干扰得到较大抑制，幅度由10×105变为2×105，经过低通滤波之后，高频高斯白噪声进一步被抑制；在国内临床心电数据中，在信噪比较低的情况下，仍能达到预期效果，且能保持源信号不失真。

5 结论

本文提出心电信号预处理方法，包括梳状滤波去除工频干扰与基线漂移、低通滤波去除高频高斯白噪声，将此方法在合成心电信号、国外MIT-BIT心电数据库、国内临床心电信号中，验证此方法的临床实用性及可行性，方法简单，容易实现，为提取胎儿心电信号提供较高的信噪比，且在信噪比较高的情况下，能保持信号不失真，达到预期效果。