东非某大型水电工程地下洞室群稳定性研究
2019-01-25章奇锋向天兵杨凡杰张传庆
章奇锋, 向天兵, 李 华, 杨凡杰, 张传庆
(1.浙江华东建设工程有限公司, 浙江 杭州 310014; 2.中国电建集团昆明勘测设计研究院有限公司,云南 昆明 650051; 3.中国科学院武汉岩土力学研究所, 湖北 武汉 430071)
1 研究背景
地下洞室群的稳定性是众多大型基建工程的关键问题。向天兵等[1]依据控制因素、破坏机制、发生条件等归纳出18种典型的围岩破坏模式,给出了各种破坏模式的主要稳定分析方法及控制措施的建议,对于现场岩体破坏模式的识别具有重要意义。冯夏庭等[2]建议采用经验类比、数值分析、智能分析等多种方法进行综合评判,从地质条件、地应力特征、围岩变形破坏机制、破坏模式的识别、开挖支护响应、监测反馈分析等开展动态设计。
在洞室稳定性分析方面,数值模拟是重要的方法之一,已经普遍应用于工程设计中解决各种岩石力学问题,其要求研究人员具备足够的知识结构及工程经验[3]。同时,岩体参数取值是数值计算的重要技术环节,在很多情况下是根据岩石块体的试验结合岩体结构条件获得[4]。
郭维祥等[5]总结了Hoek-Brown方法在中国西部若干大型水电站的科研成果及工程应用,认为该方法比传统的水电方法及Mohr-Coulomb强度理论具有更好的合理性,能够更合理描述现场实际情况和解释围岩变形破坏特征。
通过数值计算与分析,评价了K项目地下洞室群的整体稳定性,并对支护效果进行了模拟,该分析成果对后续设计及施工有重要的参考价值,也可为该地区的其他地下工程提供重要借鉴。
2 资料和方法
2.1 工程概况
东非某水电站K项目总装机600 MW,项目临近尼罗河源头,紧邻东非大裂谷,地层为前寒武系的变质结晶基底,片麻理构造明显,上覆残积层较厚,洞室埋深较浅,其工程地质条件在东非地区具有很强的代表性。
项目的主体构筑物布置于地下,由厂房、主变洞、尾调室、输水系统等组成,其中厂房尺寸为200 m×19.6 m×53 m(长×宽×高),主变洞161.4 m×14.7 m×32.95 m(厂房下游40m),尾调室320 m×21 m×70 m(主变洞下游137.7 m),中部用厚30 m的岩墙分隔成左、右调压室。
2.2 地质概况
K项目位于乌干达境内[6],距离东非大裂谷西支55 km,见图1。裂谷的扩张对工程区形成挤压效应。一般认为,自元古代至太古代(20亿年前),该区域就已经形成了稳定的大陆核心地块,被称为中非克拉通地块;该地块与其他多个克拉通地块于5.4亿年前汇聚形成了非洲板块。自寒武纪(5.4亿年)以来,本地块就保持着较强的整体稳定性,因此项目毗邻区内的地质构造不发育。工程区的地层形成于约26亿年前,并在前寒武纪的早中期发生了大面积的中级区域变质作用,形成了明显的片麻理构造。片麻理是一种流劈理构造,是在区域变质作用下,各种矿物发生压扁、拉长、重结晶等变化及定向排列[7]。一般而言,流劈理只是一种潜在的破裂面,因此,K项目的岩体普遍较完整,部分片麻理发生了断续的破裂现象。
地下洞室群由厂房、主变洞及尾调室等组成,埋深约70~90 m,上覆有效岩体厚度32~50 m(其上为全强风化层),为微风化~新鲜的花岗片麻岩,坚硬较完整为主,以Ⅱ类围岩为主,局部Ⅲ类。
本项目采用了水压致裂法测量地应力,分别在两个钻孔(孔深150 m)中进行[8]。该方法假定垂直向地应力σv为主应力之一,其量值等于上覆岩层的自重。本次测试数据分析时,参考了侯明勋等[9]关于裂缝闭合压力Ps、破坏压力Pf、重张压力Pr等关键参数的识别方法及可能导致偏差的主要因素,提高了测试精度。测试结果表明本区以构造应力场为主,最大水平主应力为8.89 MPa,方向N56~60°E,拟合公式如下,其中σH及σh分别为水平向最大及最小主应力,h为测点埋深:
(1)

图1 大地构造图示
2.3 研究方法
根据工程地质条件和构筑物布置情况,建立三维数值模型;根据岩石试验成果采用Hoek-Brown准则确定岩体力学参数,并对参数的合理性进行评价;采用三维快速拉格朗日法模拟洞室逐层开挖过程,并采用等效方法模拟系统支护效果;根据计算结果,分析围岩的应力、变形、塑性区等力学响应并评价洞室整体稳定性,提出适合本工程的开挖支护建议。
3 计算模型的建立及参数选取
3.1 模型的建立
本项目采用FLAC3D程序进行计算分析,该方法采用三维快速拉格朗日法进行计算,采用拉格朗日差分公式处理有限变形问题,允许材料发生屈服及流变,适合于解决岩土工程中经常遇到的大变形问题,已经在岩土工程界广泛应用[10]。
数值模型范围的确定主要遵循以下原则:消除边界效应的影响;充分考虑洞室开挖的实际情况和施工工序;软件的正常运行,不产生歧异结果。因此,本次模型边界按满足洞室周边围岩的厚度不小于3~5倍开挖洞径进行要求,计算范围为332 m×440 m×199 m,包括了厂房、主变洞、尾调室、引水隧洞、尾水隧洞、母线洞、出线竖井等。计算模型中,离散节点总数119 867个,多面体单元总数709 255个;岩体采用实体单元模拟,断层、节理采用接触面单元或参数等效弱化实体单元模拟,锚喷支护采用参数等效强化实体单元模拟。其中洞室群的网格模型见图2,模型四周为法向约束,底部为三向约束,地表为自由边界,地应力场采用拟合公式(1)。
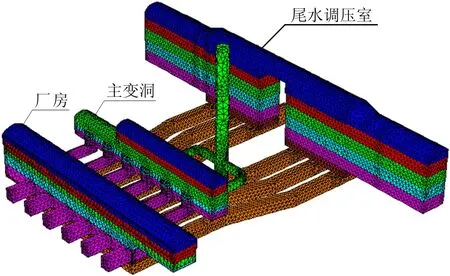
图2 地下洞室群的网格划分
3.2 岩体力学参数的确定
(1) 岩体力学参数的估算。岩体力学参数的确定是洞室稳定性研究的关键问题之一,其对开挖支护设计、稳定性评价、数值模拟的准确性至关重要。岩体原位试验的周期长、费用高、测试困难、可重现性差,难以大量开展且测试结果常呈现较大的离散性,难于应用于工程实践[11]。因此, Hoek等[12]通过几百组岩石三轴试验资料及大量现场岩体试验成果的统计分析,提出了基于GSI围岩分级系统和Hoek-Brown准则估计岩体力学参数的方法,在工程实践中具有很强的可操作性。
朱合华等[13]指出如何针对特定工程选取合适的岩石及岩体力学参数是开展工程评价、分析、设计工作等的的关键,并系统阐述了Hoek-Brown准则的发展历史及最新进展,总结了岩石及岩体参数的获取方法、参数可靠度、微观分析等问题。
Hoek-Brown破坏准则[14]已经在国际上被广泛认可,同时也是国际岩石力学学会建议的方法之一,其形式如下:
(2)
公式(2)中各参数的经验公式如下:
mb=mi·e(GSI-100)/(28-14D)
s=e(GSI-100)/(9-3D)
式中:mi与岩性有关,可以从岩块抗压强度试验成果拟合或查经验值表获得,GSI为岩体强度指标,与岩体结构及不连续面性状有关[15],D为扰动系数,与爆破控制及应力调整有关。
GSI指标是该强度准则的核心,但Hoek只给出了概化的区间范围,没有提出定量化的方法,导致GSI取值主观性较强。苏永华等[16]引入岩体块度指数、风化指数,从而对GSI的岩体结构及结构面性状进行量化,具有重要的参考价值。
另外,Hoek等[14]提出了的岩体变形模量的经验公式:
(3)
由于Mohr-Coulomb强度准则历史悠久,使用广泛,很多经典的解析表达式及数值分析软件均基于该准则,因此Hoek等[14]提出了从Hoek-Brown准则等效计算Mohr-Coulomb准则岩体参数的拟合方法,见图3。
本项目地下洞室群的岩层总体较为一致,但可细分为两种类型,见图4~6,其中A型为花岗片麻岩,是洞室内的主要地层,B型则比A型的黑云母含量明显要高,而黑云母是对岩石强度及不连续面性状有明显影响的因素,进而影响到GSI取值。
岩石单轴抗压试验采用美标[17],试验结果经尺寸修正后进行统计;综合现场地质条件,尤其是考虑黑云母含量较高对不连续面性状的影响,提出岩体的GSI值;然后应用Hoek-Brown破坏准则得到岩体力学参数,并汇总于表1。其中,岩体单轴抗压强度σc是指岩石微单元体的抗压强度,而岩体抗压强度σcm是指岩盘的整体抗压强度,计算公式如下:
σc=σci·sa
(4)
σcm=2c·cosφ/(1-sinφ)
(5)
虽然洞室内布置了位移及应力监测工作,但由于各仪器安装严重滞后,未能测得初始变形,导致最终变形量明显偏小,只能作为参考,因此本项目的岩体参数采用Hoek-Brownt破坏准则进行估算并与现场情况进行比对验证。

图3 等效Mohr-Coulomb参数的拟合方法
(2) 岩体参数估算值的验证。本工程是坚硬完整的岩体,是符合Hoek-Brown破坏准则的适用条件的。从数值计算成果可以看出,变形破坏集中于体型突变处,主要是中间岩墙及底部流道处,岩体易于破碎及松弛,这与现场调查的情况是一致的。
A型是洞室的主要围岩,岩体变形模量Em较大,数值计算表明洞室整体变形量很小,洞室稳定性良好,这是符合开挖现象及监测规律的。
B型岩石分布于局部洞段,洞室开挖后,整体稳定性良好,但观察到洞壁岩体逐渐趋于破碎的现象,而此现象在其他部位是没有发现的。从表1及数值计算结果看,B型的σc=2.8 MPa低于洞壁处的切向应力,而σcm=13.5 MPa高于切向应力,因此洞壁处的岩石会受压破碎,但岩体的整体强度是足够的。
据现场观察,中隔岩墙顶部的岩体存在着随洞室向下开挖逐渐变得破碎的现象,这是由岩体劣化造成的。由于开挖时未有效控制爆破,岩体受到严重扰动,估算岩体强度σc=7.6 MPa,σcm=22.3 MPa,而随着开挖的进行,切向应力逐渐加强,因此表层岩石逐渐受压破碎,见图7。
从上文看出,采用Hoek-Brown破坏准则估算的岩体参数后,数值计算得到的围岩破坏特征与现场情况是吻合的,表明该经验准则在低应力条件下是可靠的。
4 开挖及支护模拟
4.1 开挖模拟与分析
通过模拟地下洞室群七层开挖的施工全过程,三维数值计算获得了相应的围岩变形、应力、塑性区等分布规律,见图8~13。

表1 岩体力学参数表

图4 A型岩石(花岗片麻岩)图5 B型岩石(花岗片麻岩,黑云母含量较高)

图6岩石单轴抗压试验图7尾调室中隔岩墙顶部岩体的逐渐劣化现象

图8三维模型及位移图图9三维模型及最大主应力图图10三维模型及最小主应力图
下文以尾调室洞轴线剖面为例,分析围岩的力学响应过程。尾调室开挖完成后,围岩变形集中于体型突变处,在中隔岩墙及底部流道处的变形量约8~16 mm,两侧端墙处约7~10 mm,拱顶处约4~5 mm(图14)。
根据地应力以水平为主的特点,开挖后洞顶及底板为应力集中部位,边墙为应力松弛部位。由于地应力水平较低及洞顶圆弧轮廓等原因,因此应力集中现象不明显,洞周最大主应力约为-10~-14 MPa(图15)。
洞室开挖时,原始应力场遭到破坏,引起应力场重新调整。当洞室周边的围岩强度低于二次应力时,岩体发生破坏,无法承受较高的应力,促使最大主应力向围岩深部转移,直至在一定深度处达到新的应力平衡;此时洞壁附近出现一个围岩破坏区或损伤区,主要表现为裂隙的扩展、贯通及产生新的裂隙,并引起洞室变形。K项目的松弛区主要表现在中间隔墙、底部流道、两侧端墙等部位,但未出现明显的拉应力(图16)。应力松弛与围岩变形较大的位置基本一致,说明围岩变形主要是应力松弛导致的。
洞周的塑性区深度约为2.2~4.5 m,而在中隔岩墙及底部流道处较深,最大值约为5~7 m,这与现场情况是一致的。
综上,洞室开挖造成的二次应力、变形、塑性区深度等均不高,洞室的整体稳定性良好,适合建设地下工程;洞室体型突变及交叉部位的塑性区深度有明显增加,在开挖过程中,需要及时支护。
4.2 支护模拟与分析
锚杆、锚索是现代岩石工程最常见的支护措施。在数值模拟中,预应力长锚索采用施加节点力的方式模拟;砂浆锚杆锚固的效果与锚杆材料的强度、直径、长度以及锚杆布设的间距与方式有关,且在工程中锚杆常与喷射混凝土配合使用。因此,锚固效应主要是提高了被锚固围岩的抗剪强度,并提高加锚单元的刚度[18]。通过大量模型试验,朱维申等[19]提出了岩体抗剪强度的提高与锚杆布设参数之间的经验关系式:
c1=c0(1+ητS/ab),φ1=φ0
(6)
式中:c0、φ0、c1和φ1分别为原岩体及锚固岩体的黏聚力和内摩擦角;τ和S分别为锚杆材料的抗剪强度及横截面积;a和b为锚杆的纵、横向间距;η为综合经验系数,可取2~ 5。根据工程经验,对于K项目,可取c1=1. 33c0,φ1=φ0。
K项目各洞室的支护方式均类似,即采用锚杆加喷射混凝土,未设置锚索。以尾调室为例,其主要支护参数为:全断面系统支护,其中锚杆Φ28,L=6.0/8.0 m,间距1.5 m,混凝土喷层厚度15 cm。按设计支护方案的加固深度及处理范围,采用公式4模拟其支护效果。图17~19给出了采取系统支护后的计算成果,结果表明加固效果不明显,仅体现在位移量略有减小,而这与Barton提出的基于Q系统的支护建议[20]结论正好是一致的。
对于K项目,锚喷支护的主要作用是对应力松弛较大的部位及局部破碎岩体进行支护。对于爆破损伤造成表层岩体的劣化,锚喷支护也是很有效的。考虑到地下洞室群的极端重要性及破坏后果的严重性,把系统支护作为安全储备是合适的,在经济效益上也是值得的。
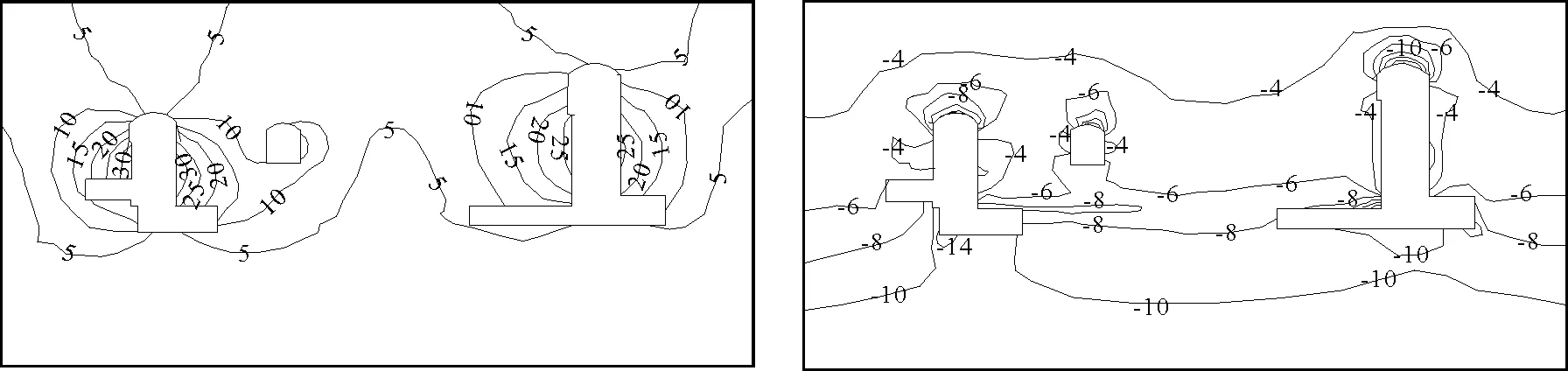
图11洞室群纵剖面位移图(单位:mm)图12洞室群纵剖面最大主应力图(单位:MPa)
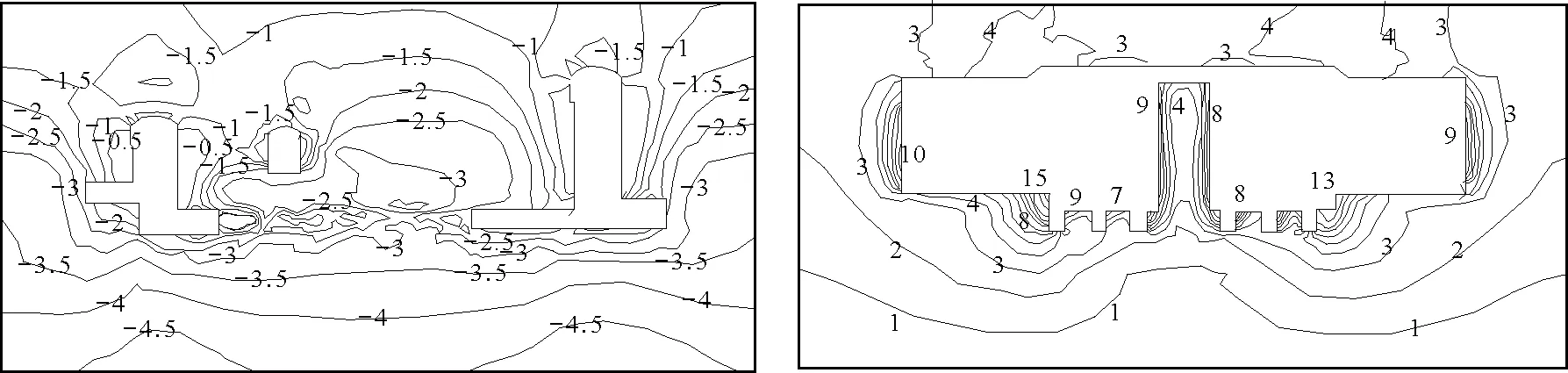
图13洞室群纵剖面最小主应力图(单位:MPa)图14洞轴线断面位移图(单位:mm)

图15洞轴线断面最大主应力图(单位:MPa)图16洞轴线断面最小主应力图(单位:MPa)

图17支护后位移图(单位:mm)图18支护后最大主应力图(单位:MPa)
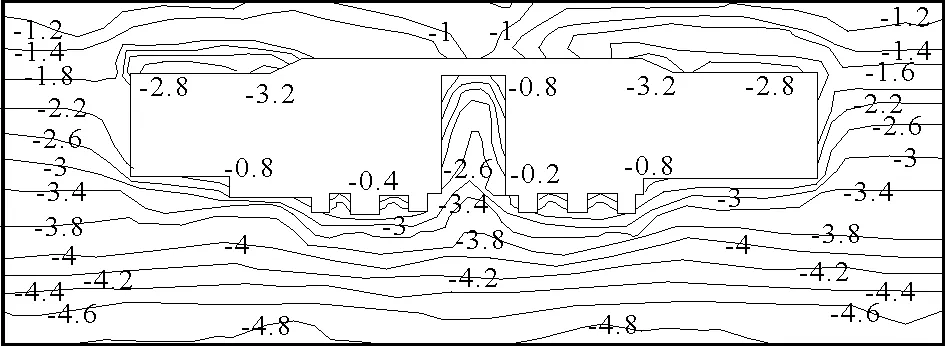
图19 支护后最小主应力图(单位:MPa)
5 结 论
(1)K项目的地下洞室群规模较大,但围岩条件较好,地应力水平中等,适合建设地下工程。
(2)根据地质条件及洞室尺寸建立三维数值模型,并模拟分步开挖过程;初始地应力采用实测值;采用等效方法模拟喷锚系统支护的效果。
(3)洞室开挖造成的二次应力、变形、塑性区深度等均不高,洞室的整体稳定性良好。
(4)应用Hoek-Brown破坏准则获取岩体参数,并把数值计算成果与现场情况进行比对,吻合得很好,表明Hoek-Brown方法是实用及可靠的。
(5)Hoek-Brown破坏准则经历了不断的修正过程,已经从经验准则上升到理论体系,并对岩体参数的确定方法提出了更高的要求,如何基于工程实际获取更加精确的岩体参数是未来的研究方向之一。
(6)K项目的工程地质条件在东非地区具有很强的代表性,因此本文的分析方法及结论具有较高的参考价值。
