黄河源区气候变化特性分析

吴 晗， 董增川， 蒋飞卿， 张 延

(河海大学 水文水资源学院， 江苏 南京 210098)

1 研究背景

19世纪以来，全球气候变化改变了全球水循环的现状，也对降水、蒸发、径流等产生了直接的影响，进而改变了水资源的时空分布，对人民生活与社会经济等造成重大影响[1]。黄河源区由于其特殊的地理位置，长期以来一直为国内外许多学者所研究。通过研究分析黄河源区气候变化，为后期径流影响、水资源演变规律、生态环境改善、植被生物保护等提供研究背景与科学依据。气候变化问题是现今社会发展中环境变化的重要问题，受到各领域学者及群众的广泛关注[2]。在当前的大背景下，研究气候变化规律与趋势，是保护水资源、维护人类社会平衡发展的重要途经之一。

黄河源区指龙羊峡水库以上的黄河流域，位于青藏高原东北部的腹地，包含青海、四川、甘肃3个省的部分城市，流域总面积13.2×104km2，研究区域如图1。黄河源区整体地势较高、气候严寒，属于高原大陆性气候。其冰川融水、雨水和冻土融水是地表水资源的重要来源，并影响着地表径流的年际变化与未来趋势[3]，是黄河的主要产流方式。近年来研究表明：受气候变化和人类活动的共同影响，源区的冻土层厚度减小、冰川消融、地下水水位不断下降、湖泊退缩与土地荒漠化等形势日益严重，促使黄河源区的径流量大多为偏枯状态[4-6]。在当地气候情况和下垫面条件的共同影响下，源区的径流量出现不同程度的减少，而其中影响最大的就是气候变化因素。同时，径流量的变化也引起了下游的供水、发电、航运、生态、水资源分布等一系列问题，给当地人民的生活带来了许多影响[7]。

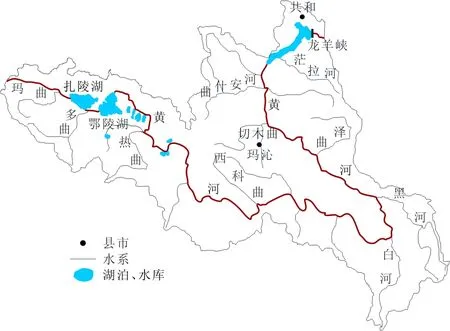
图1 黄河源区水系图

2 资料来源和研究方法

2.1 资料来源

选取黄河源区12个国家气象站点1960-2016年逐月平均气温资料与降雨资料作为黄河源区流域气象资料，气象站点分别为56021曲麻莱、56029玉树、56033玛多、56034清水河、56038石渠、56046达日、56065河南、56067久治、56074玛曲、56079若尔盖、556173红原、52943兴海，数据均来源于中国气象数据网，测站的基本信息如表1所示。

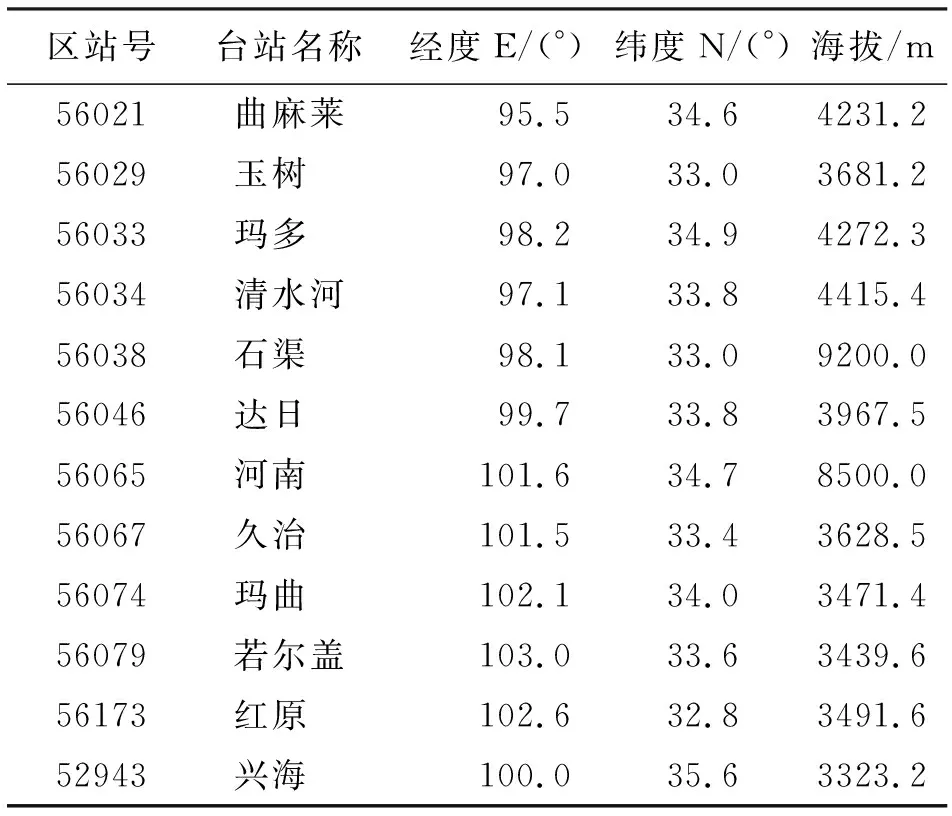
表1 黄河源区气象站点基本信息

2.2 分析方法

根据搜集到的黄河源区1960-2016年的气象资料，计算年均气温与年降雨量并组成年均气温与年降雨量序列，季节划分按照春季(3-5月)、夏季(6-8月)、秋季(9-11月)、冬季(12-翌年2月)以此计算对应季节的月均温与降水量序列。序列的突变性分析首先利用有序聚类分析法和Mann-Kendall检验法初步得出序列的突变点，然后利用滑动t法检验突变点是否合理以综合确定突变点年份。本文使用线性趋势法、Mann-Kendall检验法和Spearman秩次相关检验法对序列进行趋势性分析，并检验其显著性，最后综合各方法的结果对趋势性变化进行总结[8-13]。周期性分析运用Morlet小波分析，根据计算出的小波系数实部、小波系数模方与小波方差，绘制小波系数等值线图、小波系数模方图与小波方差图，判断序列不同尺度的周期情况、周期结构与周期强弱[14-15]。

3 结果与分析

3.1 年内气候特性分析

3.1.1 年内气温趋势分析 对1960-2016年黄河源区春、夏、秋、冬四季的月均温数据进行线性趋势法和5 a滑动平均法分析，结果如图2所示。

由图2可知，四季月均气温均呈增长态势。其中，冬季的月均温线性变化幅度最大，为0.0435 ℃/a，秋季次之为0.0336 ℃/a，春季则最小为0.0218 ℃/a。由此可见，黄河源区四季气温的增长态势均显著，其中冬季月均温增长幅度最大，春季月均温增长幅度最小。分析结果与罗栋梁等[16]的结果一致，其中冬季升温最为明显与杨特群等[17]、李晓英等[18]的结果一致，可见冬季升温对年均气温影响贡献最高。

3.1.2 年内降水量趋势分析 计算出1960-2016年黄河源区春、夏、秋、冬每个季节的降水量，并同样对其进行线性趋势法和5 a滑动平均法分析，结果如图3。

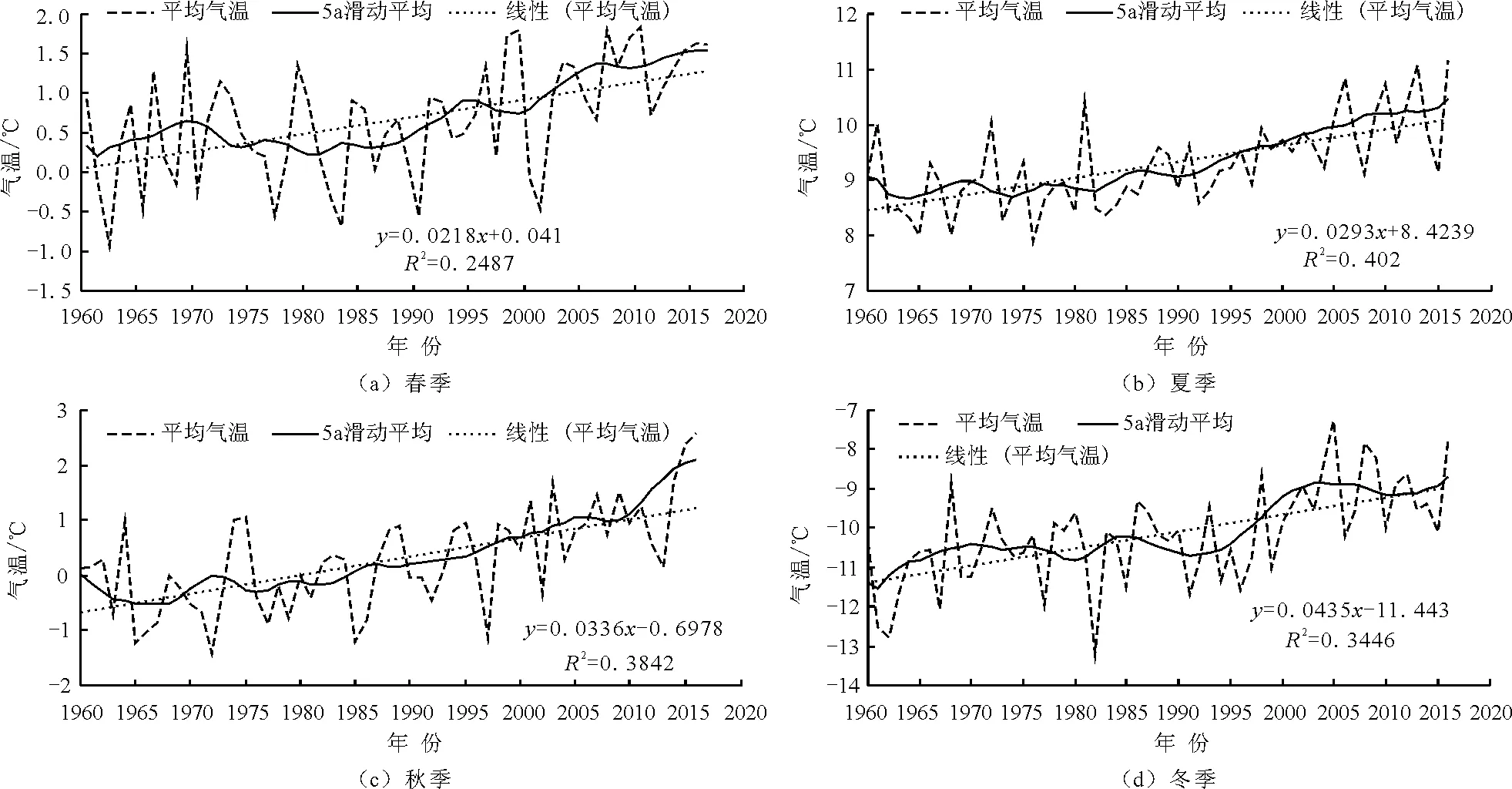
图2 1960-2016年黄河源区四季月平均气温变化趋势

图3 1960-2016年黄河源区四季降水量变化趋势

由图3可知，夏季和秋季的降水量线性变化幅度为负值，分别为-0.1594 mm/a与-0.1016 mm/a；春季和冬季的降水量线性变化幅度为正值分别为0.4712 mm/a和0.1002 mm/a。由此可见，黄河源区的降水量在春季和冬季均呈显著的增长态势，其中春季增长最为显著；而夏季和秋季降水量的下降趋势均不显著。分析结果与罗栋梁等[16]、李晓英等[18]的结果一致，其中降水量的增加量主要发生在春季，对年降水量变化贡献最高。

3.2 年际气候特性分析

3.2.1 年际气候突变性分析 首先采用有序聚类分析法分析黄河源区1960-2016年年均气温和年降水序列的突变点。计算年均气温序列和年降水序列各个年份数据的离差平方和，并在同一坐标轴下点绘离差平方和逐年变化过程，初步认定离差平方和最小值对应的年份即为突变年份。点绘出离差平方和逐年变化过程，如图4所示。

由图4可以看出，黄河源区年均气温与年降水量序列均存在离差平方和的最小值。其中，年均气温离差平方和最小值对应的年份为1997年，年降水量离差平方和最小值对应的年份为2008年。因此初步判定，黄河源区气温突变年份为1997年，年降水量突变年份为2008年。

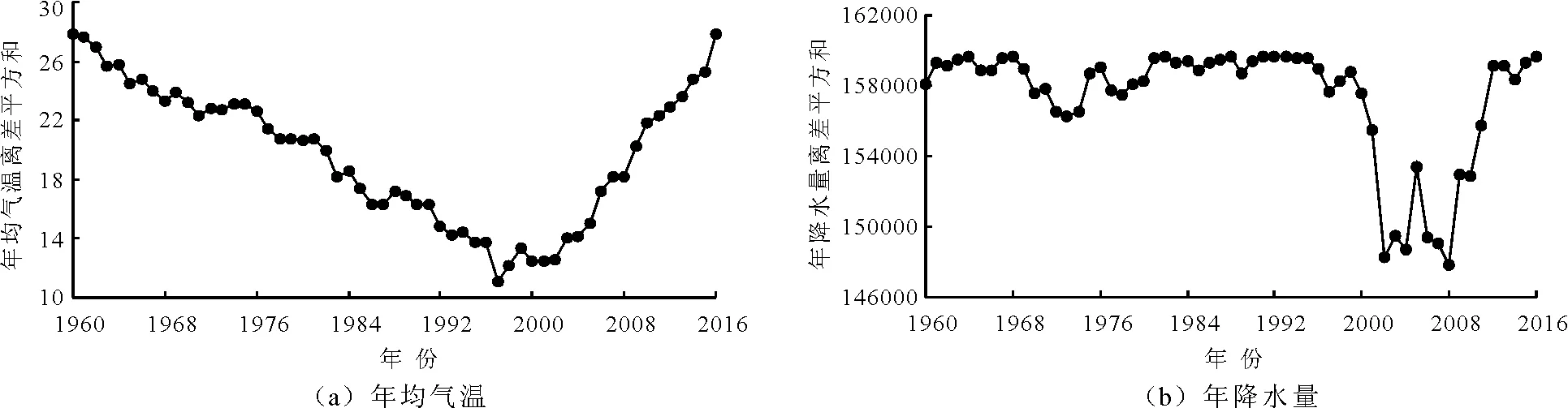
图4 1960-2016年黄河源区气候离差平方和过程图

图5 1960-2016年黄河源区气候M-K检验变化过程图

由图5(a)可知，年均气温UF与UB两条曲线存在交点为2000年，然而交点不在置信区间内未通过0.05的显著性水平。观察UF曲线可知，1966年以后年均气温序列的值都大于0，表明年均气温均呈增长态势，且1998年之后年均气温序列的值超过显著性水平0.05的临界线，证明1998年之后黄河源区的气温开始显著上升。

由图5(b)可知，年降水量变化的波动较大，UF与UB两条曲线存在交点为1961、1974、1976、1978、1985、2008、2014、2015年，且均通过0.05的显著性水平。观察UF曲线可知，1975-1996年降水量序列的值大于0，表明降水量呈增长态势，1997-2008年序列的值小于0，表明降水量呈减少态势，而2008年发生突变之后序列的值大于0又呈增长态势。

根据以上分析发现有序聚类法和Mann-Kendall检验法初步计算得到的突变点所在年份不完全一致，因此最后采用滑动t检验法对以上两种方法计算出来的突变年份进行显著性检验。将初步选定的突变年分设为基准年，分别计算前后两个序列的均值与方差，得出统计量t并判断其显著性，检验结果见表2。

表2 滑动t检验突变年份显著性结果

由表2可知，采用滑动t检验法检验有序聚类分析法和Mann-Kendall检验法初步的得出的突变点，年均气温突变点显著性较好为1997年，与罗栋梁[16]等人的结果一致，且通过了0.01的置信度检验。而年降水量的突变点显著性都较差，无明显的突变点。

3.2.2 年际气候趋势性分析 首先采用线性趋势率法和5年滑动平均法，点绘黄河源区1960-2016年年均温和年降水量的过程，添加线性趋势线及5年滑动平均变化过程线，如图6所示。

图6 1960-2016年黄河源区气候及滑动平均变化过程图

由图6(a)可知，黄河源区年均气温呈显著的增长态势，线性变化幅度为0.0318℃/a。由图6(b)可知，黄河源区降水量的增长趋势较不显著，线性变化幅度为0.3194mm/a。分析结果与白路遥等[19]的结果一致，即黄河源区年均气温与年降水量均呈增长态势，其中年均温增长显著，而年降水量序列在近20年增加趋势显著，即图6(b)中可明显看出20世纪以来降水量呈现明显的增长态势。

采用Spearman秩次相关检验法和Mann-Kendall检验法对黄河源区的年均气温和年降水量进行趋势性检验，选择显著性水平α值为0.01，相关检验结果如表3所示。

表3 Spearman和Mann-Kendall秩次相关检验法检验结果

由表3可以看出，黄河源区年均气温序列的Spearman统计量T值与M-K统计量U值都大大超过了0.01的临界值，说明年均气温递增趋势特别显著。而黄河源区年降水量序列的Spearman统计量T值与M-K统计量U值均不显著，说明年降水量无明显的递增趋势。该结果与线性趋势法分析的结果相一致。

3.2.3 年际气候周期分析 对黄河源区的年均气温和年降水量序列都分别进行Morlet小波系数实部、模方和小波方差分析。首先，将序列的数据格式进行转化，再运用Matlab软件消除或减小该序列的边界效应，最后计算新序列小波系数实部与其模方和方差，并绘制小波系数实部等值线图、小波系数模方等值线图与小波方差图，以此分析年均气温和年降水量序列的周期情况。年均气温结果如图7，年降水量结果如图8。

由图7(a)可知，黄河源区年均温序列存在着18～29、8～15以及3～7 a的3种尺度的振荡周期，其中18～29 a尺度上出现了高-低温交替的准3次震荡且具有全域性，8～15 a的尺度上出现了准9次震荡。观察图7(b)可以分析出不同周期的震荡能量，其中18～29 a尺度的周期变化能量较弱，但周期分布较明显具有全局性；8～15 a尺度的周期变化能量最强，周期分布最明显，但具有局部性20世纪90年代前比较明显；3～7 a尺度的周期变化能量也较强，周期分布很明显，也是具有局部性1975年之前与1985-2010年之间比较明显。

图7(c)小波方差图中存在着3个明显的峰值情况，依次对应于10、5与23 a。其中，最大的峰值对应着10 a的时间尺度，说明10 a左右受信号扰动最大周期震动最强，是年均气温序列变化的第一主周期；5 a为第二峰值，即为年均气温序列的第二主周期；23 a为第三峰值，即为年均气温序列的第三主周期。

图7(d)反映出不同的时间尺度下年均气温序列的平均周期及高-低温变化特征，可以看出在10 a特征时间尺度上年均气温的平均周期为6.5 a左右，在5 a特征时间尺度上年均气温的平均周期为3.5 a左右，在23 a特征时间尺度上年均气温的平均周期为14 a左右。与刘光生等[20]分析的黄河源区年均气温存在的24～28、10～12、5～8 a尺度的年际周期变化基本一致。

图7 1960-2016年黄河源区年均气温小波分析

同样由图8(a)可知，黄河源区降水量序列存在着22～32、9～14以及6～9 a 3种尺度的振荡周期，其中22～32 a尺度上出现了降水量多-少交替的准5次震荡且具有全域性，9～14 a的尺度上出现了准9次震荡。观察图8(b)可以分析出不同周期的震荡能量，其中22～32 a尺度的周期变化能量最强，且周期分布最明显，具有全局性；9～14 a尺度的周期变化能量较弱，周期分布较明显且具有局部性80年代前较明显；6～9 a尺度的周期变化能量最弱，具有局部性1995年之后较明显。图8(c)小波方差图中存在着3个峰值情况，依次对应于28、11与8 a。其中，最大的峰值对应着28年的时间尺度，说明28 a左右受信号扰动最大周期震动最强，是降水量序列变化的第一主周期；11 a为第二峰值，即为降水量序列的第二主周期；8 a为第三峰值，即为降水量序列的第三主周期。由图8(d)同样可以看出在28 a特征时间尺度上降水量的平均周期为20 a左右，在11 a特征时间尺度上降水量的平均周期为7.5 a左右，在8 a特征时间尺度上年降水量的平均周期为5 a左右。与刘光生等[20]分析的黄河源区年降水量存在的27～28、10～11、8～11 a尺度的年际周期变化一致性较高。

4 结 论

(1)年内气候特性分析选取黄河源区1960-2016年春夏秋冬四个季节的月均气温序列和降水量序列，对其进行线性趋势和5 a滑动平均分析，结果显示黄河源区四季气温的增长态势较显著，其中冬季月均气温增长幅度最大为0.0435℃/a，春季月均气温增长幅度最小为0.0218℃/a；降水量在春季和冬季均呈显著的增长态势，其中春季增长最为显著，为0.4712 mm/a；而夏季和秋季降水量的下降趋势均不显著。

(2)年际气候突变性分析通过采用滑动t检验法，检验有序聚类分析法和Mann-Kendall检验法初步得出的突变点的显著性水平，得到黄河源区1960-2016年年均气温序列突变点显著性较好为1997年，且通过了0.01的置信度检验；而年降水量的突变点显著性较差，无明显的突变点。

(3)年际气候趋势性分析分别采用线性趋势法、Spearman秩次相关检验法和Mann-Kendall检验法综合分析黄河源区1960-2016年年均气温和年降水量序列并进行显著性检验，结果显示年均气温呈递增趋势且大大超过临界值，说明递增趋势特别显著；而年降水量序列趋势性不显著，无明显的递增趋势。

(4)年际气候周期性分析对黄河源区1960-2016年年均气温和降水量序列进行Morlet小波分析、小波模方分析与小波方差分析，绘制小波系数实部等值线图、小波模方等值线图与小波方差图，结果显示年均气温存在着10、5与23 a的周期变化且10 a为第一主周期，年降水量存在着28、11与8 a的周期变化且28 a为第一主周期。