短历时强降雨下边坡滑移特征时空分布规律的研究
2019-01-25王守甲傅长锋
戚 蓝, 王守甲, 傅长锋
(1.天津大学 水利工程仿真与安全国家重点实验室, 天津 300072;2.水利部河北水利勘测设计研究院, 天津 300143)
1 研究背景
随着极端降雨出现的频率越来越大,强降雨已成为威胁边坡安全的重要因素。强降雨会导致边坡潜在滑移区内的土体快速由非饱和状态进入饱和状态,重量增加,并削弱土体强度,甚至导致滑坡等灾害的发生。通常,边坡滑移最直观的表现是特征点的位移变化,而边坡位移在强降雨下的变化与边坡的渗透特征响应直接相关,因此,研究边坡在强降雨影响下位移的时空分布规律和相应的孔隙水压力发展过程是有意义的。
降雨入渗是典型的饱和-非饱和耦合渗流问题,对其渗流特性和安全特性的研究方法主要包括室内试验、原型观测和数值模拟分析等。近年来,由于计算机技术的快速发展,数值模拟以其可重复性和操作性强的特点取得了较快发展和较多成果。宁万辉等[1]通过模型试验,发现了降雨强度、历时和地下水位是影响碎石土边坡稳定性的重要因素。付建新等[2-3]通过建立二维渗流方程并编制渗流场程序研究了二维边坡在不同降雨强度和时间下体积含水率的变化,发现降雨时长越大,则降雨影响范围越大,初始体积含水率和表层体积含水率呈负相关,和降雨影响深度正相关,这表明了土壤的干燥程度对降雨对边坡稳定性的影响很大。张社荣[4]等通过对典型边坡进行二维有限元数值模拟,研究了降雨类型、强度对边坡的孔压发展、位移变化和安全状态均有很大影响,但是,由于其所选取的边坡为典型二维边坡,所以无法考虑支护结构对边坡安全状态的影响,也无法完全反映边坡在降雨条件下的实际安全状态。付宏渊等[5-6]基于二维数值模拟,并将强度折减法引入降雨条件下的边坡稳定性计算,研究了降雨对暂态饱和区和安全状态的影响,发现饱和区发展速度及大小受雨强和持时共同影响,初始地下水位对饱和区的产生和消散有较大影响,边坡在降雨过程中的破坏是从浅层到深层逐步发展的过程,且孔隙水压力的消散会降低边坡破坏的风险。李炎隆等[7]基于ABAQUS二维有限元分析研究了降雨对分层开挖基坑边坡在降雨影响下的位移和安全系数发展的影响。
唐栋等[8]基于二维数值模拟研究了前期降雨对边坡稳定性的影响以及短历时强降雨和长历时弱降雨对边坡稳定性的影响,但没有对不同雨型对边坡安全状态做系统性的评价。田继雪等[9]基于二维数值模拟,研究了高填方边坡在短历时强降雨和长历时弱降雨下饱和区发展、安全系数变化和土体强度参数的变化,并发现长期降雨导致的土体软弱夹层的出现是高填方边坡失稳的重要原因。海龙等[10]、王俊光等[11]、金佳旭等[12]和崔亮等[13]基于二维数值模拟技术,也研究了降雨强度和历时对边坡安全系数的影响。由此可见,目前对降雨对边坡安全研究的主要对象还是二维的天然无支护边坡,主要方法是通过数值模拟研究边坡在强降雨下的饱和区演化以及不同降雨强度、历时下边坡安全系数的变化来评估降雨对边坡的影响。但是,二维数值模拟技术无法全面反映实际的边坡状态,也不能反映边坡在有支护结构的情况下,支护结构对边坡安全状态的影响,同时,对于边坡在短历时强降雨下的位移发展规律还缺乏系统性的研究,而通常在进行边坡的的降雨安全预警时,边坡位移是最容易得到的数据,因此,探讨不同的降雨类型、强度、持时对边坡位移时空分布规律的影响及降雨过程中的孔隙水压力响应是有意义的。
本文基于饱和-非饱和渗流理论,以海河沿岸某三维支护边坡为研究对象,采用ABAQUS软件对该边坡在短历时强降雨条件下的位移响应进行了系统的研究。通过对选定的典型强降雨进行分析,得到影响边坡在短历时强降雨下的最主要因素,即降雨雨型和雨强,并探究了这些因素对边坡的位移和孔压发展的影响。对边坡排水设计和在降雨条件下的预警具有一定的工程借鉴意义。
2 强降雨入渗边坡渗流基本理论
2.1 饱和-非饱和渗流计算公式
强降雨入渗条件下,边坡土体位于浸润线下的部分处于饱和状态,位于浸润线以上部分处于非饱和状态。随着降雨的持续,上部土体会逐渐由非饱和状态转变为饱和状态,这一过程是典型的饱和非饱和渗流问题。非饱和渗流问题和饱和渗流问题同样遵循达西定律,其控制方程[5]如下:
(1)
式中:h为土体空隙中的总压力水头,m;Kx、Ky分别为土体沿x、y方向的渗透系数,m/h;w为汇源项;mw为比水容重,kN/m3;ρw为水的密度,kg/m3;g为重力加速度,m/s2;t为时间,s。
2.2 非饱和土的土水特征曲线
非饱和土渗流中,土体的渗透系数同时受到孔隙比和饱和度的影响。考虑到饱和度通常与土体的化学势能直接相关,因此,饱和度通常表达为基质吸力的函数形式。本文采用的土水特征曲线函数[14]为:
kw=awkws/[aw+(bw·(ua-uw))cw]
(2)
Sr=Si+(Sn-Si)as/[as+(bs·(ua-uw))cs]
(3)
式中:kw为土体渗透系数,m/h;kws为土体饱和时的渗透系数,取为0.018 m/h;ua和uw分别为土体中的孔隙水压力和孔隙气压力,由于坡面处于大气中,这里取为0;aw、bw和cw是材料系数,本文分别取为1000,0.01,1.7。Sr为饱和度;Si为残余饱和度,本文取为0.08;Sn为最大饱和度,取1;as、bs、cs是材料参数,本文分别取为1、5 10-5、3.5。本文中渗透系数与饱和度、基质吸力与饱和度的关系曲线如图1。
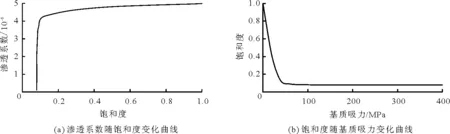
图1 土体土水特征曲线
3 有限元模型建立
3.1 工程概况
本文边坡取自天津市海河沿岸某一实际抗滑桩-挡土墙联合支护边坡,天津为典型的温带大陆性气候,降雨分布时空不均,6-9月份暴雨发生频率极高,支护边坡安全受极端降雨影响很大。边坡横剖面布置图如图2,坡顶距坡底4.89 m,边坡水平角为11.55°,抗滑桩中心距离坡顶水平距离13.19 m,坡顶宽度为6 m,挡土墙高2.05 m,底宽1.02 m,顶宽0.4 m,抗滑桩桩长8 m,桩径0.6 m,桩间距为0.6 m。考虑到对称性,采用假三维模型,即沿厚度方向取1倍桩心距。由于暴雨发生时河道多位于低水位,本文取地下水位位于墙底以下4.5 m处。布置监控点A、B、C分别位于坡顶、坡面中部和坡脚处,如图2。
3.2 本构模型及参数选取
该工程所在地层从上至下如图2,土体采用摩尔莫尔-本构模型,抗滑桩和挡土墙采用线弹性本构模型,土体和支护结构材料参数见表1。对于单
元划分,土体采用八节点六面体孔压单元,支护结构采用八节点六面体单元。对于各个部件之间的相互作用,挡土墙和抗滑桩之间采用绑定约束。支护结构与土体之间的接触采用库伦摩擦,其中法向作用采用硬接触,切向作用采用罚函数,摩擦系数计算公式为:
μ=tan(0.75φ)
(4)
式中:μ为摩擦系数;φ为与支护结构接触的土体对应的摩擦角(°)。
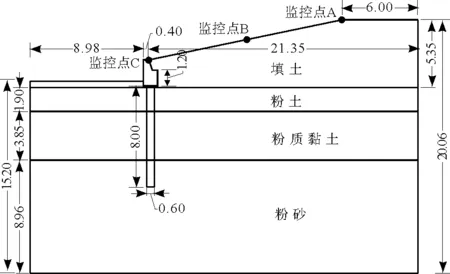
图2 边坡横剖面布置图(单位:m)

材料弹性模量/MPa土层厚度/m重度/(kN·m-3)渗透系数/10-7(cm·s-1)孔隙比泊松比土体参数C/kPaΦ/(°)填土 4.405.3519.036.70.550.2518.312.1粉土 8.281.9020.01.000.350.2517.610.2粉质黏土9.003.8518.72.950.410.2512.818.0粉砂 17.08.9619.55080.450.254.6033.0混凝土 3000024.50.20
3.3 短历时强降雨工况设计
考虑到前锋型降雨更符合天津地区夏季暴雨的实际规律,以前锋型降雨雨型研究雨强不同时对边坡滑移特征的响应,选取降雨历时为18 h,雨强依次为雨强1(5 mm/h)、雨强2(10 mm/h)、雨强3(15 mm/h)、雨强4(20 mm/h)。如图3所示,控制18 h总降雨量为220 mm不变,研究4种雨型工况下边坡滑移特征的响应行为,即后锋型、前锋型、中锋型、均匀型。
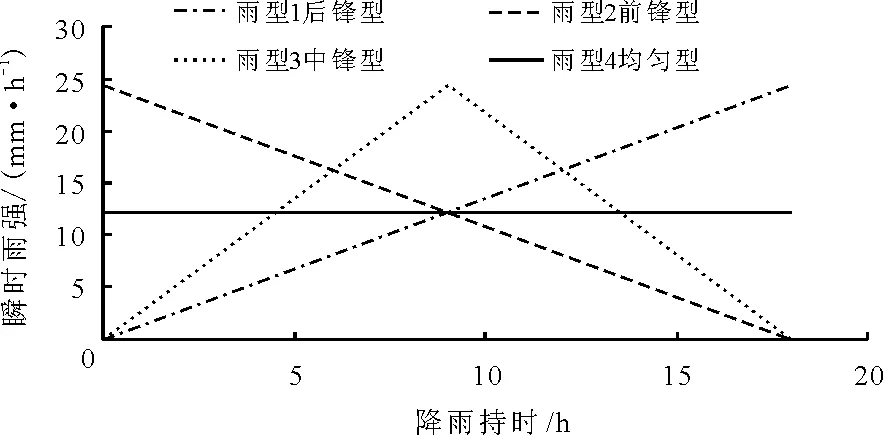
图3 短历时暴雨雨型
4 结果与讨论
4.1 短历时强降雨不同雨强下边坡位移响应
图4和5为各监控点位移随时间的发展规律,从图4、5可以看出,各监控点的水平和竖向位移发展情况呈先增大后减小的规律,同时,对于水平位移分布规律,坡脚>坡面>坡顶,对于竖向沉降,坡顶>坡面>坡脚。在到达位移最大点前,水平和竖向位移的增长速度和瞬时雨强呈正相关,与前期累计降雨量呈负相关,这是因为降雨强度越大,上部干燥土体进入饱和状态的速度也就越快,潜在滑移区内的土体重量增加越快,位移的增长速度也就越快,同时,前期累计降雨量越大,土体对于雨水的吸收能力也就越差,位移增长也就越慢。当雨强逐渐变小直至0时,潜在滑移区内的土体重量不再增大,水分持续入渗到地下水,潜在滑移区的土体越早进入饱和,则上部土体越早出现卸荷回弹,即出现位移减小的情况。
4.2 短历时强降雨不同雨型下边坡位移响应
4.2.1 不同雨型下监控点水平位移的发展规律 位于边坡斜面上的监控点A、B、C 3点随降雨时长和降雨雨型的变化,其水平位移的发展过程如图6所示,由图6可看出,不同监控点在不同雨型条件下的水平位移随时间的发展情况是类似的。空间上,水平位移分布为:坡脚>坡面中部>坡顶。时间上,后锋型降雨下,水平位移随时间单调递增,降雨后期位移增长速度变快,这是因为,后锋型降雨前期雨强较小,位移发展缓慢,后期降雨强度持续增大,上部土体迅速由非饱和状态过渡到饱和状态,重量增加,土体在重力的牵引下,位移快速增长。
对于前锋型和中锋型降雨,水平位移随时间先增大后减小,这是因为对于前锋型和中锋型降雨,前期降雨强度大,降雨快速入渗,位于潜在滑坡带内的土体快速饱和,位移发展迅速,后期降雨强度变小,且前期累计的降雨使潜在滑移区内的土体已趋于饱和,此时上部土体中的水分稳定持续补给到地下水中,上部土体重量不再增加而呈现出一定的卸荷回弹,水平位移不再发展。对于均匀型降雨,水平位移逐渐增大,但增长趋势先增大后减小,这是因为降雨后期,上部土体全部处于湿润状态时,潜在的浅层滑坡区域的重量不再增加,水平位移不再发展。

图4 不同雨强各监控点水平位移随降雨历时发展图
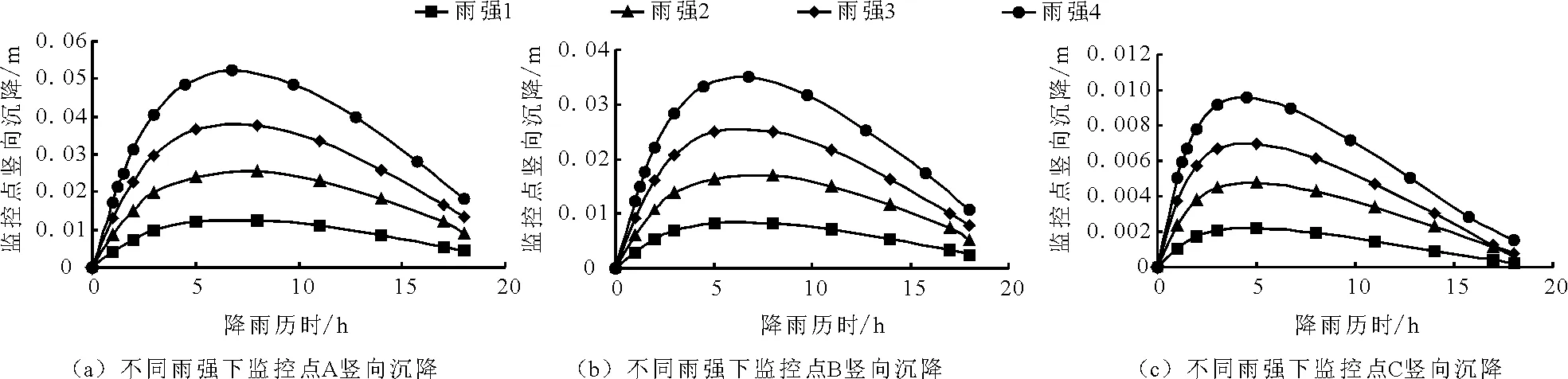
图5 不同雨强各监控点竖向沉降随降雨历时发展图
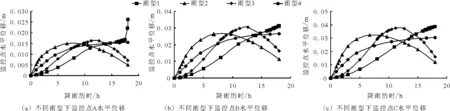
图6 不同雨型各监控点水平位移随降雨历时发展图
对于水平位移的增长速度,降雨前期,上部土体处于干燥状态,水平位移增长速度与瞬时雨强呈正相关,前锋型>均匀型>中锋型>后锋型。随降雨进行,对于前锋型和中锋型降雨,上部土体逐渐趋于饱和,潜在的浅层滑坡带重量不再增加,水平位移随土体的卸荷回弹,有一定程度的下降,此时,均匀型和后锋型降雨对应的潜在滑坡带还远未达到饱和状态,因而,位移会持续发展。可见边坡水平位移在短历时强降雨下的发展不仅与瞬时降雨强度有关,还和潜在滑移区的饱和状况及前期累计降雨量有关。
4.2.2 不同雨型下监控点竖向沉降的发展规律 监控点A、B、C在不同雨型下,竖向位移随时间的发展如图7所示,可以看出竖向位移随雨型和降雨历时的变化规律与水平位移相似。均匀型和后锋型降雨后期降雨强度呈现单调增长的趋势,且越靠近坡脚,竖向沉降越小。对于前锋型和中锋型降雨,竖向沉降表现出先增大后减小的趋势,这是由于,这两种降雨前期降雨量较大,降雨初期,上部位于潜在滑移区处于非饱和状态的土体快速进入饱和状态,降雨后期,由于浅层滑移区的土体已经达到饱和状态,其重量不再增加,而水分会持续入渗到地下水位,上部土体在应力重分布后会出现卸荷回弹现象。
4.3 典型短历时强降雨下边坡孔压响应
实例分析参照与前锋型降雨历程类似的短历时强降雨研究了在实际降雨过程中边坡的孔隙水压力发展的时空规律,该场降雨为2016年天津“7.20大暴雨”,该暴雨在18 h内平均降雨量达到220 mm,部分区县18 h降雨量达到300 mm,本次模拟取降雨历时18 h,总降雨量为250 mm。
图8为降雨过程中,边坡孔压的空间分布和发展云图。降雨前,边坡孔压沿高度方向呈线性分布,地下水位以上土体处于非饱和状态,基质吸力沿靠近坡顶方向增大。随降雨的进行,上部土体逐渐由干燥状态进入饱和状态,孔隙水压力增大,浅层土体基质吸力迅速减小直至消失,此时对应于前锋型降雨位移快速发展阶段。降雨后期,由于降雨强度逐渐减小至0,浅层土体中的水分逐渐下渗到地下水中,此时对应于位移回弹减小阶段。坡脚渗径短,所需下渗时间少,因此,孔隙水压力快速变为0,坡面和坡顶处渗径长,所需下渗时间长,同时,挡土墙和抗滑桩也在一定程度上阻挡了水分向坡脚处的下渗,因此,孔隙水压力消散速度要明显慢于坡脚。孔压的发展可以解释降雨过程中的位移发展。
5 结 论
本文基于饱和-非饱和渗流理论,采用ABAQUS软件进行了短历时强降雨下支护边坡的位移和孔压响应研究,主要结论为:
(1)边坡在短历时强降雨下位移的增长速度与雨强成正相关,与前期累计降雨量负相关。强降雨下,边坡水平位移最大处位于坡脚,竖向沉降最大处位于坡顶。
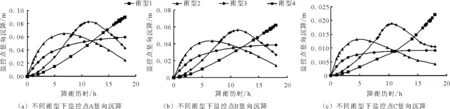
图7 不同雨型各监控点竖向沉降随降雨历时发展图
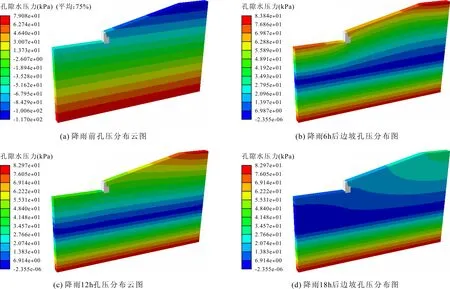
图8 降雨全过程边坡孔压分布图
(2)在总降雨量和降雨历时相同的条件下,不同雨型下最大和最终水平位移分别为中锋型和后锋型,竖向沉降随雨型和降雨历时的变化及水平位移与二者的关系呈现相似的规律。后锋型和均匀型降雨下,边坡位移随时间单调增长,后锋型降雨下位移增长速度基本不变,均匀性降雨下位移增长速度逐渐减小至0。前锋型和中锋型降雨下,位移均先增大后减小,其中前锋型降雨在前期位移发展最快,峰值出现最早,因此,应在降雨前期尤其关注边坡的滑移监测和预警。
(3)在典型强降雨过程中,浅层土体进入饱和状态的速度和平均雨强呈正相关,孔压消散时间和渗径长度呈负相关,支护结构的存在会减缓孔隙水消散速度。综上,边坡安全预警应和降雨预测相结合,充分参考可能发生降雨的雨型和雨强,预警点的选取应充分考虑不同方向的位移发展规律,支护边坡应做好排水设计以引导雨水下渗。
