注塑机用永磁同步电动机的齿槽转矩优化
2019-01-25
(广东海洋大学寸金学院,广东湛江 524000)
0 引言
塑料制品与我们日常生活密切相关,而塑料制品一般是通过注塑机注塑成型的,因此,注塑机是塑料行业主要的制造设备之一。传统的注塑机主要是通过三相异步电动机驱动,但是三相异步电动机的体积较大,效率较低,并且在运行中噪音、振动较大等缺点,而永磁同步电动机的体积小、结构简单、高效节能和起动转矩大等优点,是一种新型的高效特种电机,因此,永磁同步电动机可在注塑机中得到广泛应用[1]。
由于永磁同步电动机本身存在的齿槽转矩问题,特别是对于整数槽的永磁同步电动机则更为明显。若不能有效削弱永磁同步电动机的齿槽转矩,将会导致其输出转矩的波动较大,进而产生较大的振动和噪声,情况严重时甚至会影响到永磁同步电动机的正常运行。因此,有必要对注塑机用永磁同步电机的齿槽转矩进行优化。
首先通过分析永磁同步电动机齿槽转矩产生的原理,总结得出其齿槽转矩的表达式。根据推导得到的齿槽转矩表达式,经过分析磁极偏移与齿槽转矩的关系得出,若磁极偏移合适角度,能够明显削弱永磁同步电动机的齿槽转矩。本文以一款48槽8极注塑机用永磁同步电动机为例,利用ANSYS软件中Maxwell2D模块建立其有限元模型,为了降低其齿槽转矩,将磁极的偏移角度设为变量,在一定角度范围内进行扫描分析得到一个最佳的偏移角度,根据得到的最佳的偏移角度进行仿真分析,结果表明,磁极偏移合适的角度使该款永磁同步电动机的齿槽转矩得到明显的削弱[2、3]。
1 永磁同步电动机齿槽转矩产生机理
1.1 齿槽转矩的产生机理
若永磁同步电动机的绕组不加激励时,其铁心和永磁体之间的相互作用,可产生一个转矩,该转矩则称为齿槽转矩,通常是由永磁体和电枢齿的相互作用,产生的相互作用力中切向分量引起。在永磁同步电动机中,如果其转子和定子间存在着相对的运动,则在永磁体与永磁体极弧下的电枢齿间,其磁导基本保持恒定,所以,位于该永磁体极弧下的电枢齿周围磁场基本不变,然而,在一些由永磁体两侧面对应一个或者两个电枢齿所组成区域内,由于在该区域内其磁导有较大的变化,使磁场的储能有所变化,则形成了齿槽转矩。当永磁同步电动机绕组不通电时,其磁场能量W对于定子和转子位置角α的负导数被定义为齿槽转矩,即
(1)
1.2 齿槽转矩的解析分析
为了分析更为简便,可先作以下假设:若无特殊说明,同一电机的永磁磁钢的形状和尺寸相同、均匀分布和性能相同;永磁电机的电枢铁心磁导率无穷大;永磁材料的磁导率与空气相同,因此,得到永磁电机内所储存的磁场能量,即
(2)
由于永磁同步电动机的定、转子间的相对位置、永磁磁钢性能、结构尺寸决定其磁场能量W,沿电枢表面分布的气隙磁密可近似表示
(3)
将式(3)代入式(2),经整理可得,其磁场能量又可以表示为
(4)
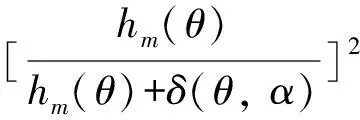
在永磁电机中,其永磁磁极是均匀分布,在区间[-π/2p,π/2p]上,Br2(θ)的傅里叶展开为
(5)
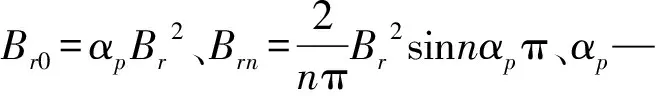
(6)
将式(4)、式(5)和式(6)代入式(1),则可得出永磁电机齿槽转矩的表达式
(7)
式中,LFe—电枢铁心的轴向长度;R1—电枢外半径;R2—定子轭内半径;n—nz/2p—整数的整数[4、5]。
1.3 分析磁极偏移与齿槽转矩相互影响
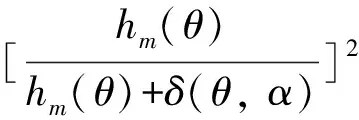
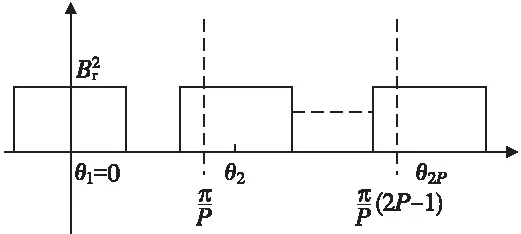
图1 永磁体偏移时Br2(θ)示意图
Br2(θ)傅里叶分解的表达式为
(8)
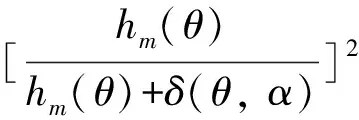
(9)
式中,Branz和Brbnz分别表示为
(10)
(11)
其中θk为第k个磁极偏移的角度,当永磁体不偏移时(即θk=0),此时Brbnz的值恒为零,此时Branz可表示为
(12)
只有当n为Np的倍数时,Branz才不为零,Np满足
(13)
式中,2p—电机极数;z—槽数,GCD(z,2p)—2p和z的最大公约数。
根据式(10)、式(11)、式(12)分析可知,当永磁体均匀分布时,只有n为Np的倍数时,则该次齿槽转矩的谐波不为零。由此可得,磁极偏移可以明显削弱槽极配合为整数的永磁电机的齿槽转矩[6]。
2 注塑机用永磁同步电动机尺寸参数及有限元模型建立
已知一款注塑机用永磁同步电动机的尺寸参数以及性能指标,如表1所示。
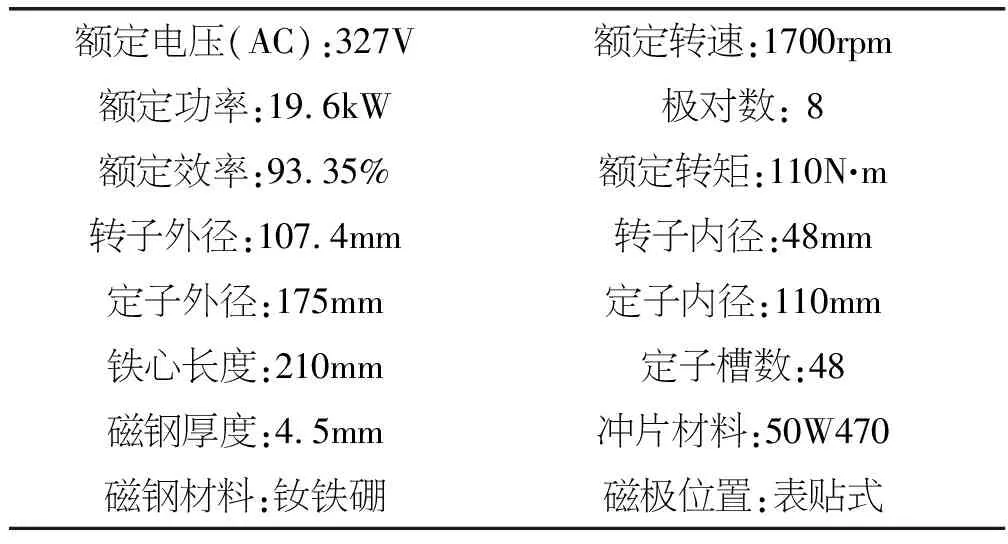
表1 注塑机用永磁同步电动机性能参数
根据表1给定的注塑机用永磁同步电动机尺寸参数,利用ANSYS软件在Maxwell 2D中建立其有限元模型,如图2所示。
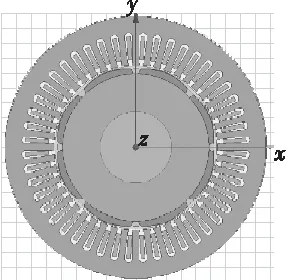
图2 注塑机用永磁同步电动机有限元模型
3 永磁同步电动机的磁极偏移分析
基于Maxwell 2D模块建立的有限元模型进行分析,由于该款永磁同步电动机的磁极对称分布,为了分析简便,可用Maxwell 2D中的1/2模型进行分析。根据建立的有限元模型,该电机磁极偏移的方向,如图3所示,即将磁极1、2按逆时针进行偏移,将磁极3、4按顺时针进行偏移,其中磁极2、3偏移角度为θ1,磁极1、4偏移角度为θ2。为了满足实际工况需要,θ1和θ2需满足θ2=3θ1,其中偏移角度θ1扫描范围可设为(0,1.1°),θ2扫描范围可设为(0,3.3°)。
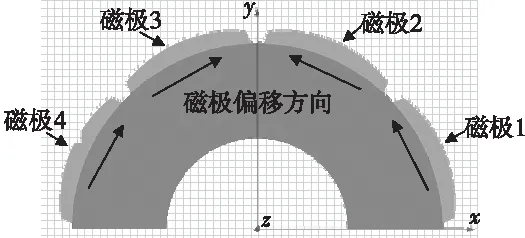
图3 磁钢偏移方向示意图
为了分析该款电机磁极偏移不同角度时,其齿槽转矩变化的情况,从而寻找最佳的磁极偏移角度使得齿槽转矩最小,利用变量参数优化法,在Maxwell 2D模块中将磁极偏移角度设为变量,在设定的磁极偏移范围内进行扫描分析,从而得到其齿槽转矩最小的磁极偏移角度,其磁极偏移不同角度时对应齿槽转矩优化曲线,如图4所示。
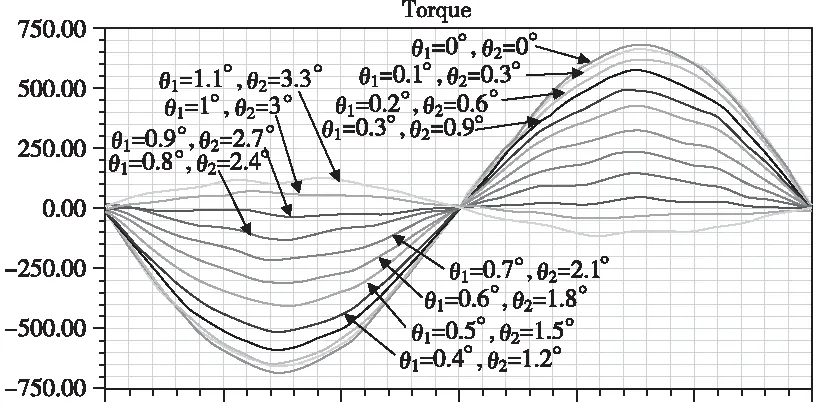
图4 磁极偏移不同角度的齿槽转矩优化曲线
利用ANSYS软件进行扫描分析,得到磁极偏移不同角度时的齿槽转矩曲线图,由此可得,各组磁极偏移角度[θ1,θ2]对应的齿槽转矩峰值,如表2所示。
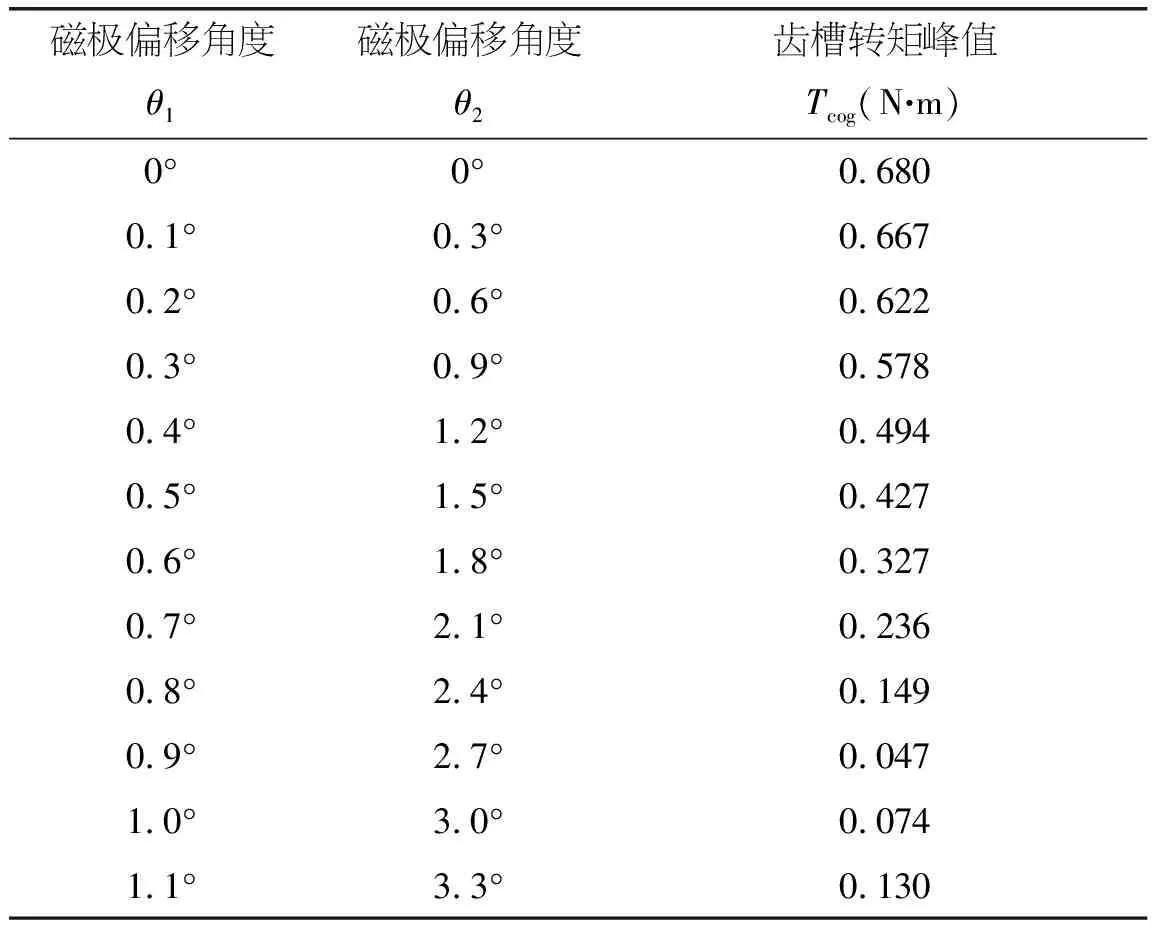
表2 各组磁极偏移时齿槽转矩峰值表
根据表2可得,永磁同步电动机的齿槽转矩峰值和其磁极偏移角度并不是呈线性递减关系。在已设定磁极偏移的角度范围内,其齿槽转矩峰值先是随着其磁极偏移角度的增加而逐渐减小,当磁极偏移到一个最佳的角度,其齿槽转矩峰值最小,若磁极偏移角度继续增加,其齿槽转矩的峰值又逐渐增加。因此,将磁极偏移到最佳偏移角度时可使其齿槽转矩减低到最小值,该款注塑机用永磁同步电动机最佳偏移角度为:磁极θ1偏移0.9°,磁极θ2偏移2.7°,其齿槽转矩峰值仅为0.047 N·m[7]。
4 注塑机用永磁同步电动仿真结果及分析
利用有限元分析软件Maxwell2D模块进行扫描分析,选取齿槽转矩峰值最小的一组[θ1,θ2]为磁极最佳偏移角度,仿真分析得出该款注塑机用永磁同步电动机的磁极偏移和未偏移的齿槽转矩曲线,如图5所示。
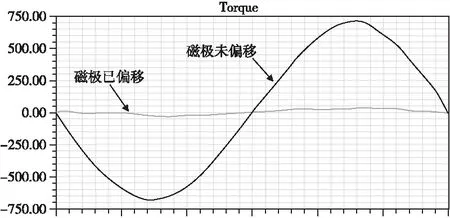
图5 磁极未偏移和已偏移的齿槽转矩曲线
根据图5得出,该款注塑机用永磁同步电动机磁极未偏移时,其齿槽转矩峰值为0.710 N·m,当磁极偏移到最佳角度,得到其齿槽转矩峰值仅为0.038 N·m,故齿槽转矩峰值降低了0.672 N·m,而且当磁极偏移后,其齿槽转矩峰值仅占额定输出转矩0.035%。将磁极偏移后的注塑机用永磁同步电动机进行仿真分析,得到其输出转矩曲线,如图6所示。
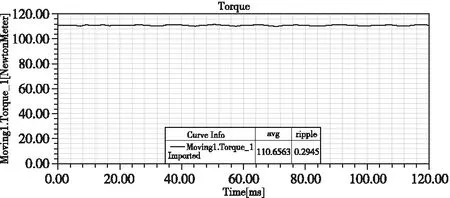
图6 注塑机用永磁同步电动机输出转矩曲线
根据图6得出,通过对该款注塑机用永磁同步电动机的磁极偏移合适角度后进行仿真,得到其平均输出转矩为110.66 N·m,而且转矩波动仅0.2945 N·m,仅为其额定转矩0.27%,由仿真结果可知,经过优化后,该款注塑机用永磁同步电动输出转矩平稳。
5 结语
本文目的是削弱一款注塑机用永磁同步电动机的齿槽转矩,改善其性能,通过将磁极偏移的方法来降低该款永磁同步电动机的齿槽转矩。基于变量参数优化法,利用ANSYS软件中的Maxwell 2D模块进行扫描分析,选择最佳一组偏移角度[θ1,θ2],即[0.9°,2.7°]进行仿真,仿真结果表明,该款电机经过优化后,其齿槽转矩降低了0.672N·m,仅占额定转矩0.035%,而且其平均输出转矩为110.66N·m,其转矩波动仅为0.2945N·m,占其额定转矩0.27%。因此,若要降低注塑机用永磁同步电动机的齿槽转矩,可采用磁极偏移的方法来实现,且优化后该款永磁同步电动机的输出转矩平稳,各项性能指标较好。该文为优化注塑机用永磁同步电动机齿槽转提供了一定的参考价值。
