融合超像素和伪流算法的交互式图像分割

瞿绍军，李乔良，陈 明，谭 煌

1(湖南师范大学 信息科学与工程学院，长沙 410081)2(湖南师范大学 数学与统计学院，长沙 410081)

1 引 言

近年，交互式图像分割在计算机视觉领域得到了人们的广泛关注，图割是最流行的交互式图像分割方法.Boykov和Jolly[1]第一次在离散域中构建简单的生成MRF模型，用于处理二值图像分割任务，这是交互式分割的基本模型.指定一些目标和背景像素作为用户先验约束，可以通过图割方法高效地求解全局最优解.该方法基本原理是将能量最小化问题转化为基于图的最大流问题，主要优势在于全局最优、实际效率高，缺点是容易产生孤立割集.为了避免最小割在图中分割出孤立节点集合.Shi提出利用归一化割(Ncut)[2]评价不同组之间的不相似性，以及组内的总体相似性.Ncut方法可以稳健地生成平衡簇，并且优于其他谱图分割方法.Tao等人[3]开发了一种基于均值漂移和Ncut方法的彩色图像分割方法.Yu和Shi[4]扩展Ncut来处理硬性必连约束(must-link)，Eriksson等人[5]提出利用Ncut来处理硬性的必连约束和勿连约束(cannot-link)，Subhransu Maji[6]提出了一种修改的“归一化割”，将先验引入图像分割，可认为是一种修改的Ncut解决方法，以软方式来满足必连约束.Chew[7]重新形式化Ncut(Semi-Supervised Normalized Cuts：SSNCuts)，以便以软约束方式处理必连约束和勿连约束，使用户能够调整约束满足的程度.

超像素图像分割是Malik和Ren在2003年提出和发展起来的一种图像分割技术[8]，是指具有相似颜色、纹理、亮度等特征的相邻像素构成的有一定视觉意义的不规则像素块.它利用像素之间特征的相似性将像素分组，用少量的超像素代替大量的像素来表示图像特征，很大程度上降低了图像后处理的复杂度.常用的超像素图像分割方法有：Turbopixel[9]、均值漂移(Mean shift)[10]、SLIC[11]等.甘玲等提出一种基于SLIC超像素初始分割和区域合并的交互式图像分割方法[12]，程仙国等提出融合SLIC与改进邻近传播聚类的彩色图像分割算法[13]，都获得了较好的分割结果.

最小s-t割问题是一个经典的组合优化问题，它是许多视觉和成像算法中的一个重要构建模块.Hochbaum在文献[14-17]中介绍了伪流算法并将伪流算法应用于求解最小s-t割问题，与push-relabel、增光路径算法和部分增广路径-重标记算法在执行时间与内存利用率方面进行了理论对比和实验验证.实验结果表明，伪流算法比这三种算法更高效并且使用更少的内存.这对于许多需要解最小s-t割问题的实时计算机视觉问题，伪流算法是一个很好的选择.

本文受Chew的半监督归一化割[7]启发，提出将超像素和伪流算法融合进行图像分割.在所提出的方法中，交互信息由用户以粗略地指示少部分目标和背景位置，然后使用SLIC[11]对图像进行超像素分割，再以每个超像素作为图中的一个顶点进行构图，采用与论文[7]中一致的gPb(globalized probability of boundary)[18]计算超像素之间的相似性，最后用伪流算法进行超像素分割，并将超像素分割结果转换到原始像素和图像得到最终分割.由于在分割中计算gPb非常费时，严重影响到分割效率，本文进一步用均值漂移进行超像素分割和Bhattacharyya系数[19]计算超像素之间的相似性，实验结果显示，本文提出的方法既提高了分割的准确性，又提升了分割的效率.

2 半监督归一化分割方法

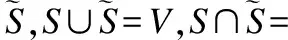
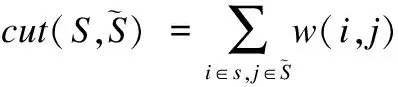
(1)

图的最优的分割是最小化(1)的割值.在图的划分过程中，先验知识告诉我们应该将某些顶点划分在一起，某些顶点不应该划分在一起，分别称它们为必连约束和勿连约束.

必连约束：假设知道集合C={(vil，vjl)|l=1，…，m}表示两个顶点应该分组在同一划分中.一个修改的违反必连约束的惩罚的割的成本形式：

(2)

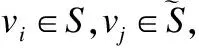
(3)

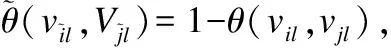
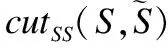
(4)

通过以下方式定义半监督归一化割(SSNCuts)成本：

(5)

3 伪流算法

近年来，Hochbaum在基于图的分割方面做出了突破性的工作，文献[14-17]中介绍了伪流算法并将伪流算法应用于求解最小s-t割问题.她将该算法与push-relabel、增广路径算法和部分增广路径-重标记算法在执行时间与内存利用率方面进行了理论对比和实验验证.实验结果表明，伪流算法比这三种算法更高效并且使用更少的内存.Hochbaum对归一化割、等周常数、Cheeger常数、conductance等问题之间的关系进行了系统的分析，证明了在离散变量上最小化Rayleigh比问题是多项式时间可解的.对这些问题可以表示成不同的正交约束下的离散变量上的Rayleigh比问题[20].传统上，这些问题利用谱方法启发式求近似解.该文还提出了一个新的约束割集问题——次归一化割集问题，这一问题是多项式时间可解的.因此，Hochbaum伪流算法算法可以给出比谱方法更好的对归一化参数的估计.将上述结果应用到归一化分割，可以得到更好的分割效果.

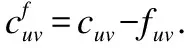
最大流问题定义在有向s，t-图Gst=(Vs，t，Ast)，标准形式的最大流问题用变量fij表示弧(i ，j)上流的总量.

maxfts
满足 ∑ifki-∑jfjk=0，∀k∈Vs，t
0≤fij≤cij，∀(i，j)∈Ast

(6)

公式(6)中目标函数值，也是离开源(或到达汇)的总流，表示为|f|，第一个约束(等式)叫流平衡约束.第二个约束(不等式)叫容量约束.一个“预流”可违反流平衡约束，在一个方向允许非负过剩(流出的小于流入的)，∑ifki-∑jfjk≤0.而“伪流”可能在两个方向违反流平衡约束.容量约束都是满足的.

使用动态树数据结构的伪流算法如[14-17]具有O(mnlogn)的时间复杂性，之后被改进到O(mnlog(n2/m)).

4 基于超像素和伪流算法的图像分割

首先由用户交互引入目标和背景的先验信息；其次分别使用SLIC和均值漂移对图像进行超像素分割(产生的超像素个数为n)；再以每个超像素作为一个顶点建立邻接矩阵(邻接矩阵大小为n*n)，分别用gPb[18]和Bhattacharyya系数[19]计算超像素之间的相似性；最后利用伪流算法进行超像素分割，并将超像素分割结果转换到原始像素和图像得到最终分割.其过程如图1所示.

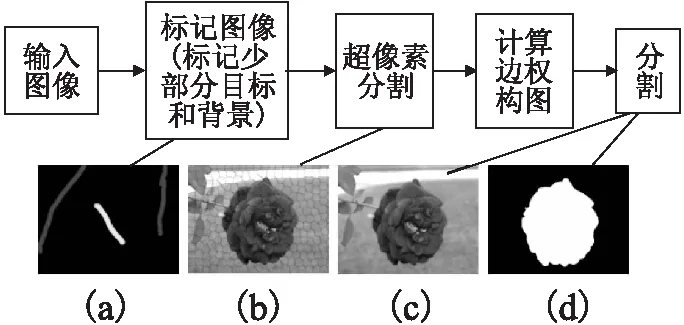
图1 交互式图像分割过程Fig.1 Interactive image segmentation process

4.1 目标和背景标记

在交互式图像分割中，用户需要指定目标和背景像素或区域，用户可以通过绘制线条、曲线和涂鸦输入交互信息.图1(a)展示了通过使用简单的曲线标记目标和背景像素，使用白色标记来表示目标，用浅黑色标记来表示背景.

4.2 生成超像素

在提出的方法中，需要先将图像分割成许多区域(超像素)以提供初始分割.首先选择与 SSNcuts一样的SLIC进行初始分割，之后进行改进和实验比较，使用均值漂移方法进行初始分割.图1(b)显示了SLIC初始分割的一个例子.SLIC中参数选择和SSNcuts论文中保持一致，取regionSize=10，regularizer=10000.均值漂移中的参数，根据论文作者建议，取Spatial=7，Color=6.5，MinimumRegion=20，对绝大部分图像都能得到比较好的预分割结果.

超像素生成后，根据目标标记，找到具有目标种子像素的超像素区域，并将这些顶点对应的超像素区域作为新的目标种子点集合(ObjectSet，ObjectSet={i|超像素i中至少一个像素∈目标种子点}).根据背景标记，找到具有背景种子像素的超像素区域，并将这些顶点对应的超像素区域作为新的背景种子点集合(BackgroundSet，BackgroundSet={i|超像素i中至少一个像素∈背景种子点}).

4.3 计算超像素之间相似性

以每个超像素作为一个顶点来构造图，用图的边权来表示超像素之间的相似性关系.分别用gPb和Bhattacharyya系数两种方法计算超像素之间的相似性.

1)gPb定义图的边权.在每个像素计算边界的全局化概率(gPb)，找出8个方位角上的最大gPb，并定义超像素i和j之间的权重为[7，18]：

(7)

如果‖pi，j‖≤r，则Wi，j=0，否则，Pi，j是连接超像素i和j的质心的线段，ρ是常数. 将r设置为图像宽度和高度的最大值的0.1倍.ρ设置与论文[18]一致，取ρ=0.1.

2)Bhattacharyya系数定义图的边权.由于计算gPb对硬件配置要求非常高，并且耗时，严重影响分割效率，在改进实验中使用RGB颜色空间来计算颜色直方图，将每个颜色通道统一量化为16个等级，然后在16×16×16 = 4096个bins的特征空间中计算每个超像素的直方图.Hi表示超像素i的归一化直方图.然后定义两个超像素i和j之间的相似性度量W(i，j)，以提供各超像素之间的比较，这里选择使用Bhattacharyya系数[19]来衡量i和j之间的相似度：

(8)

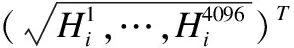
如果超像素的个数为n，则权矩阵W的大小为n×n.

4.4 构 图

给定图G=(V，A)，V是顶点的集合，包括产生地超像素共n个节点、新增终端节点S与T，A是边的集合，包括两类边：

第1类边是超像素顶点之间的关系，即任意两个超像素块之间的相似性.对任意两个超像素i和j，如果Wi，j>0，则超像素i和j之间连接一条边Ai，j，其权值设为Wi，j*1000.因4.3节中计算出的权是归一化的权，其值的大小在0～1之间，而伪流计算的时候需要整数权，通过实验分析，当权值扩大到100-1000倍，分割结果的趋于稳定，因此，实验中对W扩大1000倍，即W=1000*W.

第2类边是终端节点S到标记为目标种子点的边和终端节点T到标记为背景种子点的边.对任何目标种子点集(object)，设置As，object=INFINITE_FLOW，对任何背景种子点集(background)设置AT，background=INFINITE_FLOW.INFINITE_FLOW是一个很大的数，如108.权值越大，表示分割的时候一条边关联的两个顶点越不应该被分开.其边权设置方法如表1所示.

表1 边权计算方法Table 1 Calculation of edge weight

图G建好后，利用伪流算法计算最优解，获得最优的分割.最后，将超像素分割结果转换到原始像素和图像得到最终分割，结果如图1(c)所示，其二值掩码分割结果如图1(d)所示.

5 实验对比及结果

为了定性和定量的评估采用伪流算法之后对分割质量的改善，在标准数据集上进行对比测试，图片选自Berkeley分割数据库[21]和MSRA显著对象数据集[22]共250张图片，包括背景较单一，纹理较少，背景比较复杂，纹理较多，前背景颜色非常相似等图片.MSRA显著对象数据集本身提供了二值分割真值，Berkeley分割数据库中图片的二值分割真值来自Kevin[23]提供的96张图片的真值.

5.1 与SSNCuts对比实验

通过几组不同图片对SSNCuts进行分割实验，其中约束条件选取必连约束+勿连约束组合情况，从中选取最好的分割结果，如图2所示.

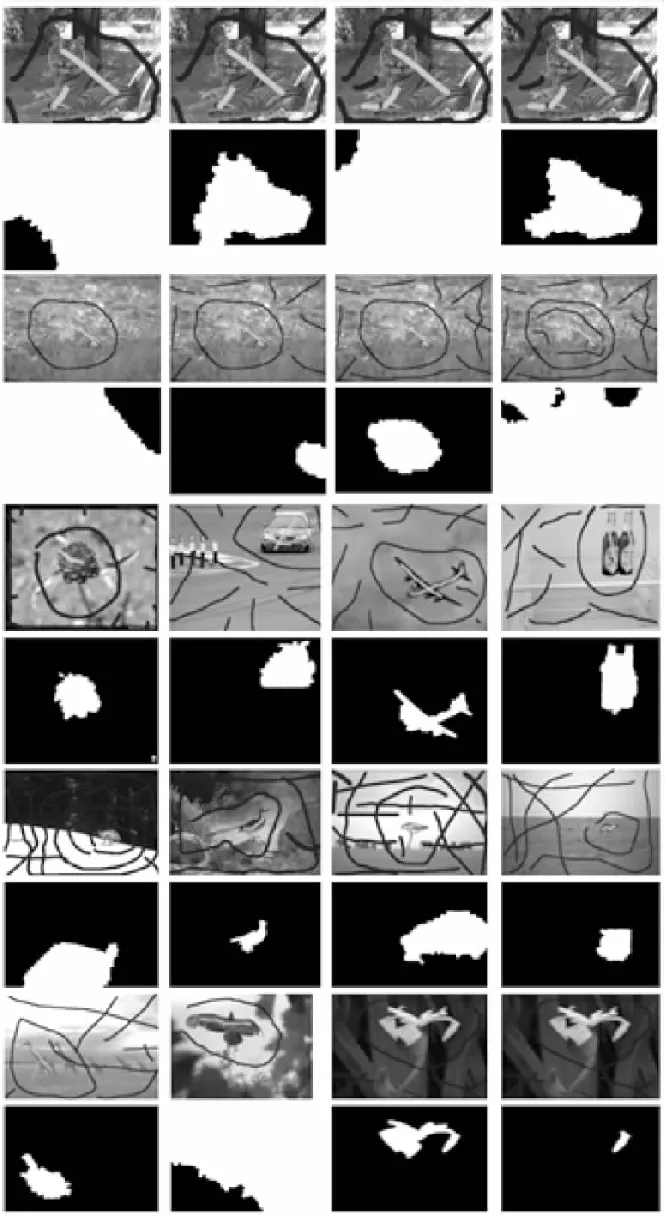
图2 SSNCuts分割结果Fig.2 Segmentation results of SSNCuts

在图2(第1、第3行图片)，人工不断修改标记，从分割结果可以发现，SSNCuts方法对标记的选取非常敏感，标记相差不大的时候，但对分割结果影响非常大；当图片中目标和背景颜色非常相似，纹理复杂分割效果不好；从分割过程来看，标记非常费时和困难，标记种子点的时候，无法预测分割的结果，不能保证标记为目标区域的像素分割为目标，标记为背景的像素分割为背景.当图片背景较为单一时(图2中第5行图片)，图片中目标较小的时候(图2中第7行图片)，图片中存在多个相似的目标(图2中第9行第1列)，要得到较好的分割效果也很困难.在图2中第9行第2列，SSNCuts将图片边界的区域误分成目标或背景.在图2中第9行第3列，花朵左边中间有小部分背景，SSNCuts将其误分为目标，在图2中第9行第4列，在误分为目标的背景上增加背景标记，分割结果更差了.

本文提出的方法一是SLIC、gPb和伪流算法的融合(简称SGH)；二是Mean shift、Bhattacharyya和伪流算法的融合(简称MBH)，对图2中图片分割结果如图3所示，从实验结果来看，整体优于SSNcuts.

5.2 目标精确性指标评价

目标精确性指标又称Jaccard 相似性系数[24].计算公式如下：

(9)

其中S是真值分割，S’是算法的分割结果.通过Jaccard相似系数来量化分割的准确性，提出的方法和SSNcut比较结果如图4所示.

图3 本文提出方法对图2中图片分割结果(a)和(d)为原始图片(b)和(e)为SGH分割结果 (c)和(f)为MBH分割结果Fig.3 Results of our method in Fig.2

从实验结果可以看出，对绝大部分图片，当超像素分割和计算超像素之间的相似性与SSNcuts一致时，当超像分割使用均值漂移，计算超像素之间的相似性使用Bhattacharyya系数时，提出方法的分割准确性都高于SSNcuts方法.在分割效率方面，由于计算gPb对硬件配置要求非常高，并且耗时，对分辨率为400*300左右大小图像，在Intel Xeon CPU E5-2680 v2 2.80GHz、32GB内存的机器上测试，计算gPb需要60秒左右的时间，严重影响分割效率.而采用Bhattacharyya系数定义图的边权，在普通计算机上分割时间一般都在2秒内完成，大大提高了分割的效率.因此，基于伪流和超像素的分割方法整体上优于SSNcut.

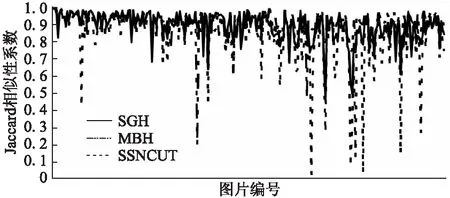
图4 三种方法的Jaccard相似性系数比较Fig.4 Jaccard similarity coefficient comparison results of the three methods

提出的方法与SSNCuts在图片集上更多分割结果比较如图5所示，整体上来看，提出的方法优于SSNCuts.

提出的方法与SSNcut的主要区别：

1)SSNcut中采用软形式的必连约束和勿连约束，提出的方法采用硬性必连约束和勿连约束，保证了标记为目标区域的像素分割为目标，标记为背景的像素分割为背景.

图5 提出方法与SSNcuts分割结果比较(a)原始图像，(b-d)分割结果.(b)MBH，(c)SGH，(d)SSNcutsFig.5 Comparison of our method with SSNcuts

2)构图和优化方式不同，SSNcut使用谱方法求解，提出的方法使用伪流优化求解.

3)采用Bhattacharyya系数定义图的边权比gPb具有更高的的效率.

5.3 与多种主流算法比较结果

提出的方法进一步与OneCut[25]，Random Walker (RW)[26]，Normalized Random Walker(NRW)[27]，Normalized Lazy Random Walker (NLRW)[27]，Pseudo-Bound Optimization (PBO)[28]五种方法进行了比较，评价指标采用Precision(查准率)，Recall(召回率)，F-Measure和ME(平均错误率).F-Measure定义为查准率和召回率的调和平均值：

(10)

其中，β是用来确定查准率对于召回率的重要性，一般设置取β2=0.3使得查准率略高于召回率.

给定两个有限点集S和S′，ME定义为：

(11)

p1表示S和S′对应位置像素标签是背景的数量.p4表示S和S′对应位置像素标签是前景的数量.r和c分别表示图像的宽度和高度.实验中为了显示的方便取ME=1-ME.

图6显示了平均查准率、平均召回率、平均F-Measure和平均错误率.

1)平均查准率比较：MBH的值为0.960，SGH的值为0.962，KL_PBO略高于本文提出的方法，其值为0.967，其它方法都低于本文提出的方法.

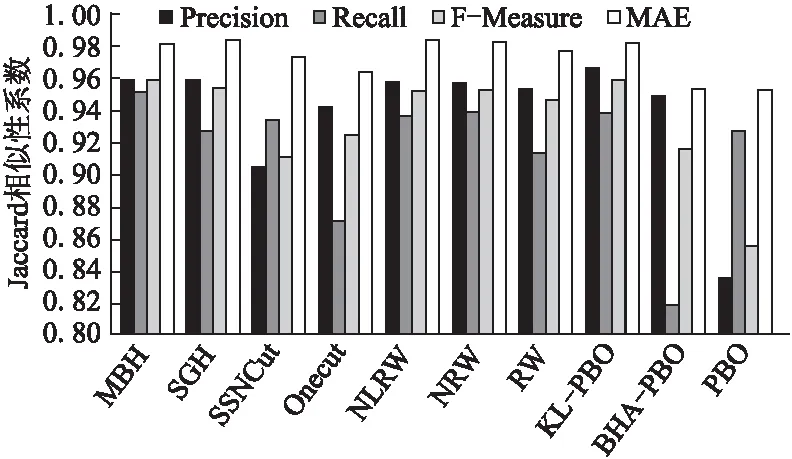
图6 平均precision、recall、F-Measure和ME比较Fig.6 Average precision，recall，F_Measure and ME comparison

2)平均召回率比较：MBH的值为0.951，SGH的值为0.928，SSNCUT的值为0.934，NLRW的值为0.936，NRW的为0.939，KL_PBO的值为0.938.SSNCUT、NLRW、NRW和KL_PBO略高于SGH，最高的为MBH.

3)平均F-Measure比较：MBH的值为0.958，SGH的值为0.954，KL_PBO略高于本文提出的方法，其值为0.960，其它都方法都低于本文提出的方法.

4)平均错误率比较：MBH的值为0.982，SGH的值为0.983，NLRW的值为0.982，NRW的为0.983，KL_PBO的值为0.982，其它方法都低于0.982.综合来看，本文提出的方法在几种指标上都取得了较好的结果.

6 总 结

本文提出将超像素和伪流算法结合起来进行交互式图像分割，提出的算法有效的解决了SSNcut分割的缺陷：当目标和背景颜色相似，或纹理复杂的图片分割时效果不佳，对标记的种子像素非常敏感等问题，提高了分割精度，获得了很好的分割结果.通过使用Bhattacharyya系数计算超像素之间的相似性，大幅度获提高了分割的效率.进一步的研究是将伪流算法运用到多个目标的分割和语义分割.