融合特征降维和密度峰值的二进制协议数据帧聚类算法
2019-01-24闫小勇
闫小勇,李 青
(信息工程大学 信息系统工程学院,郑州 450000)
1 引 言
二进制协议区别于文本类协议[1],面向比特定义字段、数据帧结构紧凑、控制开销小、传输效率高,因此在物联网、数据链等场合中应用广泛.尤其是用户自定义的二进制协议,出于各种原因不公开协议规范,在网络中占有相当的比例[1].二进制协议大多通过UDP协议承载传输,不形成会话流,传统的面向流的分类识别算法无法有效解决这一问题.自定义字符集的使用,导致很难利用定界符等先验信息[1],进行频繁模式提取.同时,灵活的字段长度定义[1],要求统计分析需要以比特为单位,这在一定程度上缩小了协议数据帧之间的差异.这些特点都使得二进制协议分类识别相比于文本类协议更加困难.
刘兴彬[2]等基于Apriori算法提取特征字符串和包长特征用于协议识别,但因Apriori算法需要多次扫描数据库,并且会产生大量的候选项,导致算法整体的计算效率和可扩展性较差.Wang[3]等采用X-means方法对会话流聚类,然后对每个簇的主导应用建立分类模型.黄笑言[4]等基于字节熵矢量加权指纹实现二进制协议识别,以不同字节对协议识别的贡献不同进行加权并完成聚类.Luo[5]等提出基于粗糙集的协议识别方法,利用最小描述准则实现聚类簇数的自适应确定.Yue[6]等利用AC算法提取频繁项,使用Apriori算法挖掘关联规则,最后采用改进的K-means算法实现二进制数据帧聚类,但因频繁特征挖掘范围不易确定,导致聚类的粒度很难掌控.
上述网络协议识别方法大多面向会话流、以字节宽度对协议数据做统计分析[2-5],虽然对二进制协议识别有一定效果,但更偏向于文本类协议.本文面向二进制私有协议数据帧,提出了一种融合特征降维和密度峰值的二进制协议数据帧聚类算法(Feature Dimensionality Reduction based on Frequent Items-Density Peaks Clustering based on Distance Index Weighting,FIFDR-DIWDPC).主要贡献有:
1)提出基于频繁项的特征降维算法(Feature Dimensionality Reduction based on Frequent Items,FIFDR),在降维的同时保留了能够区分不同协议数据的信息;
2)提出基于距离指数加权的密度峰值聚类算法(Density Peaks Clustering based on Distance Index Weighting,DIWDPC)自动选取聚类中心,有效提高了聚类中心和其它数据帧的区分度.
本文剩余部分组织如下:第二节建立了问题模型;第三节详细阐述了算法细节;第四节对算法本身进行仿真与实验分析,并与经典算法进行对比;第五节结论.
2 问题模型
二进制协议根据设计目标和应用背景的不同,其所定义数据帧长度存在很大差异.就同一协议而言,由于帧用途不同,会有多种帧长.即使同一类数据帧,仍会存在可扩展字段,导致帧长可变.
对于变长帧,以比特为处理单位计为一维特征,则数据帧的维数通常会从上百维到上千维,其中包含大量冗余信息[7,8].为提高聚类的性能,需要进行特征选择.
对于接收到的数据集,可能是不同协议数据帧的混合,也可能是同一协议下不同帧格式数据帧的混合.由于先验信息缺失,数据集的真实类别数目和类别中心很难确定[9].
因此,实现二进制私有协议数据帧的聚类需要解决数据帧预处理、冗余信息去除和无监督条件下聚类中心、聚类簇数的自动确定等关键问题,如图1所示.
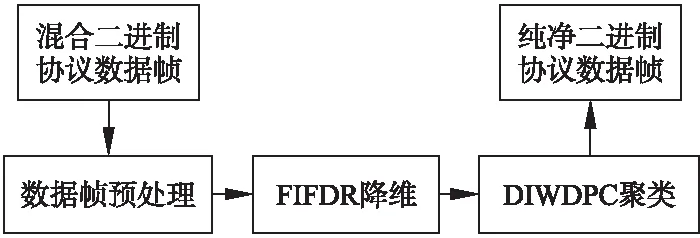
图1 FIFDR-DIWDPC算法流程图Fig.1 Workflow for FIFDR-DIWDPC
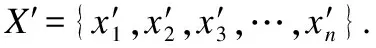
3 FIFDR-DIWDPC算法
3.1 数据帧预处理
由于3.2节中利用滑动窗提取频繁项的过程中,当协议数据帧长度不是滑动窗长度的整数倍时,协议数据帧末尾的若干比特信息将会丢失.为了避免信息损失,采用给长度非滑动窗长整数倍的协议数据帧末尾补0的方式,使得协议数据帧的长度为滑动窗长整数倍,如式(1)所示.szeroi表示第i条协议数据帧末尾补0的个数,|xi|表示数据帧xi的比特长度,win_size是滑动窗长,mod为数学中取余运算.
szeroi=win_size-(|xi|modwin_size)
(1)
3.2 基于频繁项的特征降维算法
绝大部分协议报文中存在关键词,关键词能够用于区分不同的协议报文[10-12].关键词通常在协议报文中频繁出现,提取频繁项,构造特征矢量用来表示协议数据帧能够实现协议数据帧降维.基于频繁项的特征降维算法主要包含两个步骤:
1)利用滑动窗实现不同偏移位置处的频繁项统计,构造携带偏移位置信息的频繁项集合;
2)对照频繁项集合将协议数据帧转化为特征矢量,实现协议数据帧降维.
步骤1中频繁项的提取涉及到支持度,用bstring(j)表示携带偏移位置信息的比特串,bstring为比特串,长度与滑动窗长win_size相同,j为bstring的起始比特相对于协议数据帧首部的偏移位置,则支持度的定义如下:
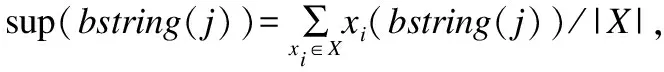
设置最小支持度阈值minsupport,当sup(bstring(j))>minsupport时,bstring(j)为频繁项.由于本文面向混合二进制私有协议,协议的种类和数量未知,为了尽可能的识别混合数据集中的协议,通常minsupport取值较小.
如图2所示,设滑动窗的长度为4比特,滑动窗w1,w2,w3,…,wk-1,wk的起始位置对应于协议数据帧首部的偏移量分别为0,4,8,…,(k-2)×4,(k-1)×4.假设由支持度定义获取的频繁项共有四个,分别为0001(0),0001(8),0101(8),0110((k-2)×4).由图可以看出,同一个滑动窗可能产生多个不同的频繁项,相同的比特串在不同的滑动窗中代表不同的频繁项.将得到的频繁项按照位置先后进行排序,得到频繁项集合F_item={f_item1,f_item2,…,f_items}.将原始数据帧对照频繁项集合,若频繁项存在于数据帧中,即xi(bstring(j))=1,则将bstring(j)在频繁项集合F_item中的对应序号(若f_item2=bstring(j),则对应序号为2)添加到数据帧的特征矢量.图2中,第1帧、第i帧和第m帧的特征矢量分别为:(1,2),(1,4),(1,3).
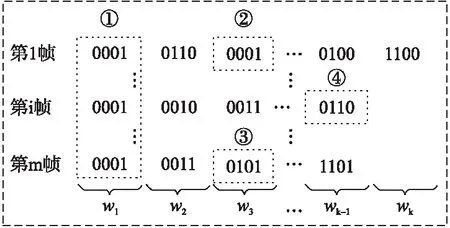
图2 特征降维Fig.2 Feature dimensionality reduction
基于频繁项的特征降维算法,利用数据帧中包含的频繁项来表示原有的协议数据帧,达到协议数据帧降维的目的.因为协议关键词通常在协议报文中频繁出现,通过频繁项构建特征矢量降维原始高维数据帧,能够保留用于区分不同协议数据帧的信息,从而实现后续混合协议数据帧的聚类.
3.3 基于距离指数加权的密度峰值聚类算法
鉴于大部分聚类方法存在聚类中心和聚类簇数无法自动确定的问题,本文改进密度峰值聚类算法(Density Peaks Clustering,DPC)[13],提出基于距离指数加权的密度峰值聚类算法DIWDPC,利用最长公共子序列距离度量数据帧之间的相似性,重新设计了γ,并采用统计学中识别异常值的方法选取聚类中心.
3.3.1 相似性度量
不同协议数据帧中包含的频繁项数量可能不同,因此3.2节得到的降维后的数据帧维度不同.对于不等长的降维数据帧之间的距离不能使用欧氏、马氏距离计算,本文采用最长公共子序列距离衡量降维数据帧之间的距离.距离公式如式(2)所示.dij表示数据帧yi和数据帧yj之间的距离,LCSS(yi,yj)表示数据帧yi和数据帧yj的最长公共子序列.
(2)
最长公共子序列通常使用动态规划的方法求解.由于降维后的数据帧用频繁项在频繁项集合中的序号来表示,因此数据帧中不包含重复的元素.最长公共子序列LCSS(yi,yj)等价于yi和yj的交集,式(2)可以简化为式(3).
(3)
3.3.2 密度、距离计算及参数确定
DPC算法的基础是对聚类中心的两点假设:
1)聚类中心被密度均不超过它的邻居包围;
2)聚类中心与其它密度更大点之间的距离较大.
为此,算法给每个点定义了两个属性:密度ρ和距离δ,ρ值和δ值都大的点才有可能成为聚类中心.
关于密度ρ,文献[13]给出了Cut-off kernel和Gaussian kernel两种形式.Gaussian kernel考虑了数据点之间距离对密度ρ的影响,本文选择Gaussian kernel作为密度计算公式,如式(4).其中dij是数据帧yi和数据帧yj之间的距离,dc为距离阈值.
距离δ表示数据点与密度更大数据点的最小距离,如式(5).
(4)
(5)
距离阈值dc是DPC算法的一个重要参数,该参数直接影响密度ρ的计算,如式(4).协议数据中存在完全相等的数据帧,导致不同数据帧之间距离为0的情况较为普遍.dc的确定依赖于帧间距离,为了使dc大于0,本文确定dc的方法与文献[13]有所不同.首先过滤掉距离为0的数据,再通过文献[13]的经验估计方法选取dc,具体过程如式(6)-式(9).
A={dij|j>i,dij≠0}
(6)
A′=sort(A)
(7)
p=[perc×|A′|]
(8)
(9)
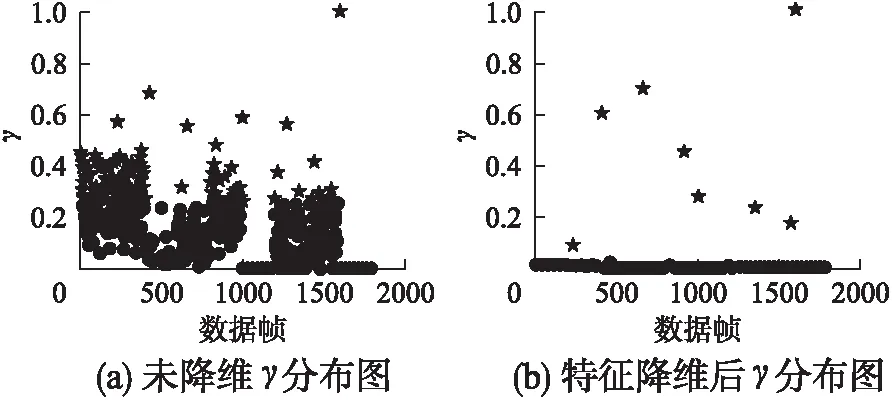
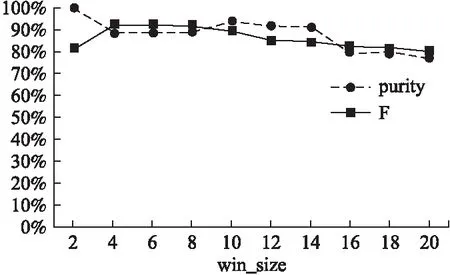
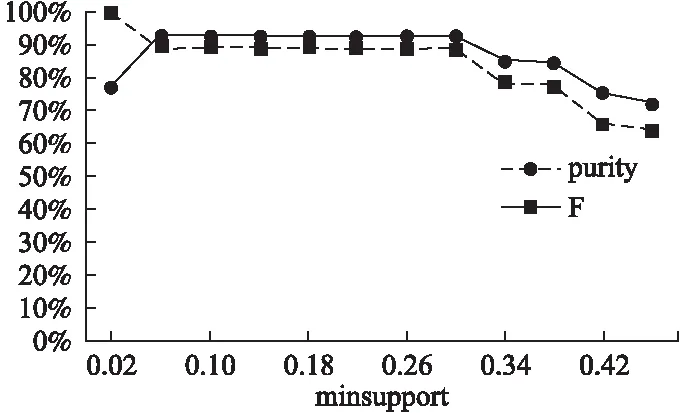
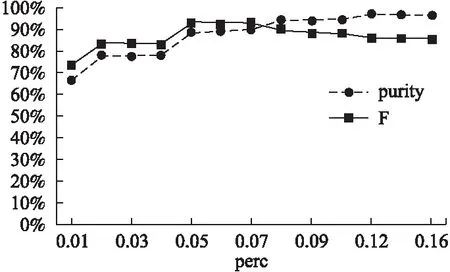
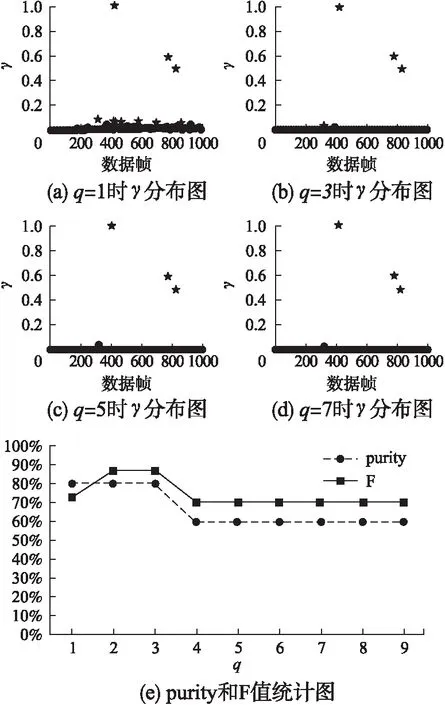
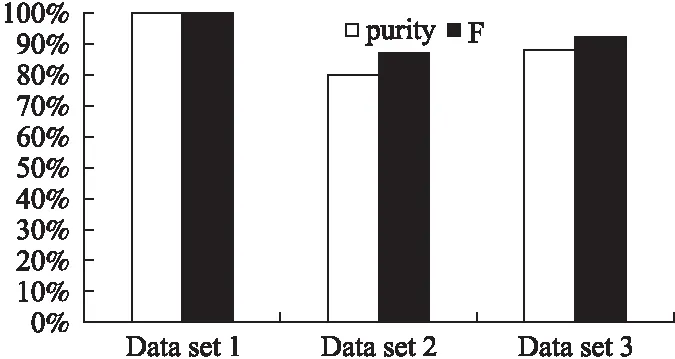
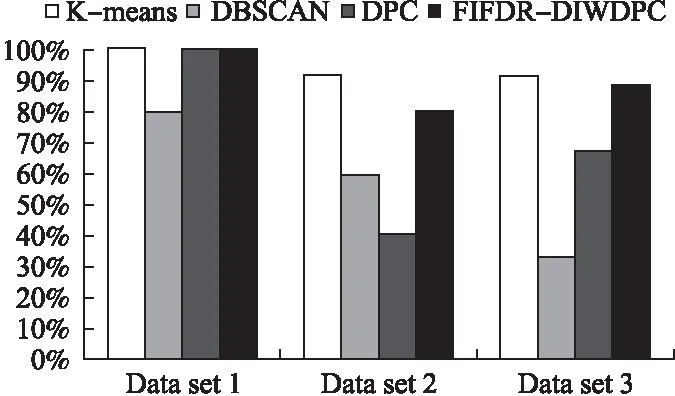
A是帧间距离的集合,A′是A的升序排列,p是A′的索引,0.05 3.3.3 基于距离指数加权的聚类中心选取算法 由3.3.2节所述,ρ值与δ值均大的数据帧有可能是聚类中心.因此,文献[13]定义γ=ρ×δ,γ值大的数据帧为聚类中心. 本文认为δ值大的数据帧要比ρ值大的数据帧更可能成为聚类中心.因为通常数据帧的分布密度多样,ρ值大于聚类中心ρ值的数据帧较多,而δ值大于聚类中心δ值的数据帧较少.图3是数据集2的ρ-δ分布图(数据集2在第4小节中详细介绍),五角星标注的点为可能的聚类中心.可以发现,δ值大的点只有几个聚类中心,而ρ值大的点有很多,因此δ值在聚类中心选取过程中比ρ值具有更好的区分性,δ值大的点更可能成为聚类中心.为了更好的选取聚类中心,本文重新设计了γ,如式(10).γi表示第i条数据帧的γ值. (10) 图3 ρ-δ图Fig.3 ρ-δ graph 新设计的γ考虑到ρ值和δ值可能处于不同的数量级,在计算γ的过程中对两者进行了归一化处理,即每条数据帧的ρ值和δ值分别除以ρ和δ的最大值.γ中对δ进行了q次方的处理,且要求q>1,体现了δ值的重要性,使聚类中心能够更好的区别于其它数据帧. 由于聚类中心的γ值相对于非聚类中心点的γ值属于过大值,因此可以使用统计学中检测异常值的方法提取聚类中心,如式(11). N={yi|γi-μ>σ} (11) N为聚类中心集合,μ为γ的均值,σ为γ的标准差.统计学方法中认为检测值和均值的差值超过两倍标准差时为异常值,超过三倍标准差时为高度异常值.为尽可能提取聚类中心,本文通过不同数据集上多次试验验证认为γ值和均值μ的差值超过一倍标准差时即可作为聚类中心. 3.3.4 聚类 确定聚类中心之后,数据帧被分配给比它密度高并且距离它最近的数据帧所属的类,如式(12)所示. (12) (13) Cc和Hc分别表示第c个簇的核心点与边界点集合.最终的聚类结果如式(16)所示,li表示聚类之后第i条数据帧的类标签.li为0时,表示该点没有被分配类标签,视为噪声数据. (14) (15) (16) 为了验证FIFDR-DIWDPC对不同协议数据帧的区分能力, 构造数据集1,如表1所示,由五种不同协议的单种帧格式数据帧构成.为了验证FIFDR-DIWDPC对同一协议下不同 表1 数据集1 协议数据帧格式数量(帧) AISType4200 ARPRequest200 DNSRequest200 ICMPType11200 SMB200 帧格式数据帧的区分能力,构造数据集2,如表2所示,由AIS协议的五种不同帧格式数据帧构成.为了更贴近实际,构造数 表2 数据集2 协议数据帧格式数量(帧)Type1200Type3200AISType4200Type6200Type18200 据集3,如表3所示,由AIS协议的五种不同帧格式数据帧和其余四种协议的单种帧格式数据帧共同构成. 表3 数据集3 协议数据帧格式数量(帧)Type1200Type3200 AISType4200Type6200Type18200 ARPRequest200 DNSRequest200 ICMPType11200 SMB200 实验过程中主要涉及四个参数win_size、minsupport、perc和q,设置如式(17)~式(20). win_size=4 (17) minsupport=0.1 (18) perc=0.06 (19) q=3 (20) 本文采用两种常用的评价指标:纯度purity和F值,如式(21)和式(24)所示. 纯度purity: (21) F值: (22) recall和precision分别表示召回率和准确率,nt表述数据帧中属于第t个类别的帧个数,nc表示数据帧中属于第c个簇的帧个数. (23) F(t,c)表示第t个类别和第c个簇之间的F值,总的F值为: (24) 4.1.1 FIFDR算法参数分析 图4是FIFDR-DIWDPC在数据集3上的运行结果,图4(a)和图4(b)中五角星标注的点为选取的聚类中心.图4(a)是在没有降维的条件下,对预处理后的数据帧直接应用DIWDPC得到的γ分布图.图4(b)是采用特征降维后再使用DIWDPC得到的γ分布图.对比图4(a)和图4(b)发现降维对聚类中心的选取影响较大,数据帧降维后再做聚类,冗余信息得到有效去除,聚类中心与其它数据帧区分性增强. 图4 降维对聚类的影响Fig.4 Influence of dimensionality reduction on clustering 1)滑动窗长win_size分析 图5为FIFDR-DIWDPC在数据集3上,win_size不同取值下的purity和F值统计.可以发现,4≤win_size≤8时,purity和F值稳定且相对较大.win_size>8以后,purity和F值整体成下降趋势.这与二进制协议数据帧的特点密切相关,二进制协议数据帧以比特定义字段,数据统计和分析的最小单元为比特,不受字节长度限制,因此在win_size小于8时,算法性能良好.当win_size大于8以后,随着win_size不断增长,能够提取的频繁项数量逐渐减少,算法整体性能开始下降.本文在大部分情况下,win_size设置为4. 2)支持度阈值minsupport分析 图6是FIFDR-DIWDPC在数据集3上,不同minsupport取值下的purity和F值统计.minsupport的取值与原始数据集中包含的协议种类数有关.minsupport取值较小,降维效果将不明显;minsupport取值较大,数据集中占比较小的协议数据帧的频繁项将无法通过minsupport获取,从而对聚类结果产生影响.从图6中可以看出,参数minsupport具有较强的鲁棒性,0.06≤minsupport≤0.30时,purity和F值均较大且稳定.minsupport>0.30以后,随着部分协议数据的频繁项无法被提取,由特征矢量表示的协议数据帧开始丢失可区分不同协议数据帧的信息,表现为purity和F值开始下降. 图5 不同win_size下的purity和FFig.5 Purity and F under different win_size 图6 不同minsupport下的purity和FFig.6 Purity and F under different minsupport 4.1.2 DIWDPC算法参数分析 1)参数perc分析 图7是在数据集3上,win_size取值为4,minsupport取值为0.1,q取值为3,不同perc取值对应的纯度purity和F值.可以看出perc取值在0.05到0.07之间时,纯度purity和F值均较大,本文设置perc为0.06. 图7 参数perc对聚类的影响Fig.7 Influence of perc on clustering 2)距离指数q分析 图8(a)至图8(d)是在数据集2上,win_size取值为4,minsupport取值为0.1,perc为0.06,q分别取1,3,5,7时的γ分布图.图8(e)是相应的纯度purity和F值.可以看出,q取值为1时,通过本文算法提取的聚类中心较多,与实际偏差较大.q取值为3时,聚类中心由原来的多个变为了4个,与真实情况接近.q取值为5和7时,图中最左边的聚类中心点随着q的增加逐渐消失,通过本文算法最终只能得到三个聚类中心点.由图8(e)可以看出q取值为2和3时,纯度purity和F值均取得最大值,而后随着q值的增加,两者均开始下降,最终保持平稳,本文设置q为3. 图8 参数q对聚类的影响Fig.8 Influence of q on clustering 4.1.3 FIFDR-DIWDPC算法整体性能分析 图9是在三个数据集上,FIFDR-DIWDPC算法的纯度purity和F值.数据集1是不同协议单种格式数据帧的混合,差异性较大,FIFDR-DIWDPC不仅能够准确识别协议的种类,同时能够将各数据帧正确划分到所属的类,纯度purity和F值均达到100%.数据集2由AIS协议的5种不同帧格式数据帧混合而成,同种协议不同帧格式数据帧差异性较小,较难区分,纯度purity和F值有所下降.数据集3既包含不同协议的数据帧,同时包含同种协议不同帧格式数据帧.FIFDR-DIWDPC算法能够识别不同协议的数据帧,但对于同种协议不同帧格式数据帧识别性能稍差.因为纯度purity和F值是整体性能的衡量指标,所以算法在数据集3上的整体性能优于在数据集2上的性能. 图9 FIFDR-DIWDPC算法整体性能Fig.9 Overall performance of FIFDR-DIWDPC 图10 purity统计图Fig.10 Purity graph of different algorithms 图11 F值统计图Fig.11 F graph of different algorithms FIFDR-DIWDPC算法在不同协议数据帧聚类中性能良好,而在同一协议不同帧格式数据帧聚类中与经典算法相比优势明显.该算法能够克服冗余信息对二进制协议数据帧聚类的影响,保留能够区分不同协议数据的信息,并且实现了聚类中心和聚类簇数的自动确定,达到了二进制协议分类识别的目标. 假设待聚类的数据集有n条二进制数据帧,数据帧维度为m.DPC算法时间复杂度依赖于三部分,分别是数据帧与数据帧之间的距离计算时间(时间复杂度为O(mn2/2));数据帧的局部密度ρ计算时间(时间复杂度为O(n2));数据帧的距离δ计算时间(时间复杂度为O(n2)).所以DPC算法的整体时间复杂度近似为O((m/2+2)n2).FIFDR-DIWDPC算法时间复杂度主要由FIFDR时间复杂度和DIWDPC时间复杂度两部分构成.FIFDR的时间复杂度近似为O(n×「m/win_size⎤).DIWDPC时间复杂度由三部分构成,数据帧与数据帧之间的距离计算时间(时间复杂度为O(n2/2));数据帧的局部密度ρ计算时间(时间复杂度为O(n2));数据帧的距离δ计算时间(时间复杂度为O(n2)).因此FIFDR-DIWDPC算法的时间复杂度近似为O(n2).K-means算法的时间复杂度近似为O(n),DBSCAN算法的时间复杂度近似为O(n2). 本文提出的融合特征降维和密度峰值的二进制协议数据帧聚类算法FIFDR-DIWDPC,能够在无监督条件下实现二进制协议数据帧的分类识别.通过在AIS、ARP、DNS、ICMP和SMB五种协议数据构成的三个数据集上测试,具有不错的效果.该算法的局限性在于对数据集中不同类型协议数据的频繁项提取还不够准确.因为本文面向混合二进制私有协议,数据集中协议的种类和数量未知,若存在小类样本,而通过设定的支持度阈值无法提取该小类样本的频繁项,那么最终的聚类结果中将不包含该小类样本协议.如何克服小类样本对聚类的影响是未来需要研究的课题.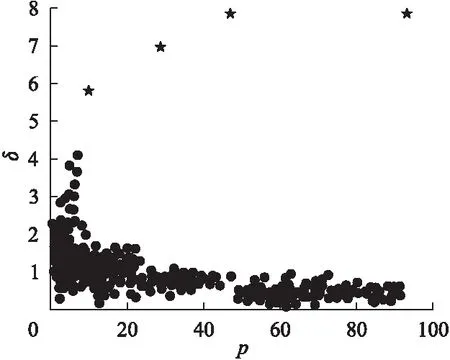
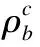
4 仿真与实验分析
Table 1 Data set 1
Table 2 Data set 2
Table 3 Data set 3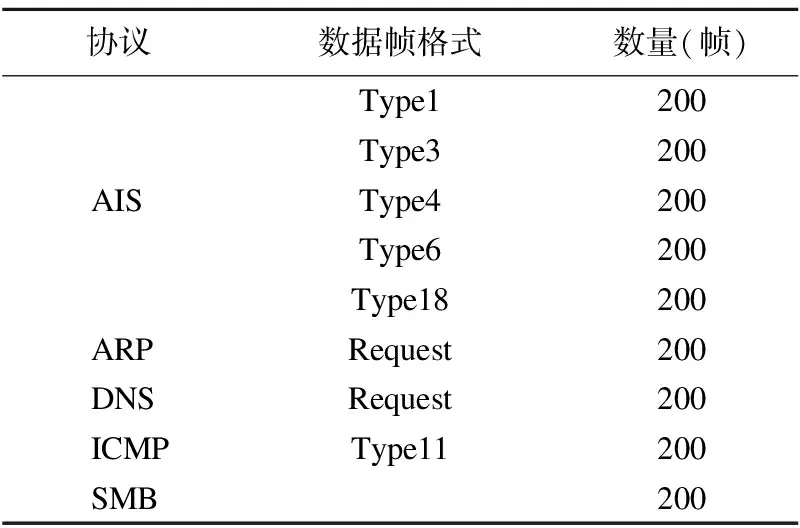
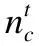
4.1 FIFDR-DIWDPC算法参数及性能分析
4.2 与经典算法的性能对比
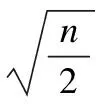
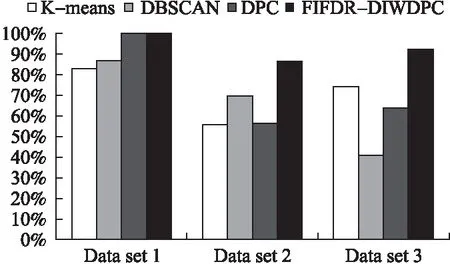
4.3 算法时间复杂度分析
5 结 论
