一种动态调整惯性权重的简化均值粒子群优化算法

黄 洋，鲁海燕，2，许凯波，沈莞蔷，2

1(江南大学 理学院，江苏 无锡 214122)2(江南大学 无锡市生物计算工程技术研究中心，江苏 无锡 214122)

1 引 言

粒子群优化(particle swarm optimization，PSO)算法[1]是一种基于对群体捕食行为进行模拟研究的群体智能优化算法.自1995年提出以来，PSO算法已受到众多学者的关注并已在现实优化问题当中得到了广泛的应用[2-4].然而，PSO算法也存在早熟收敛以及在算法搜索后期收敛速度慢等不足.为了改善这些不足，国内外众多学者提出了不同改进策略的粒子群优化算法.其中，对粒子群优化算法中更新公式的改进成为众多研究热点之一.文献[5]通过对粒子群优化算法中惯性权值递减策略的研究，分析了4种常用的惯性权重调整策略的性能特点.文献[6]提出了一种随机权重取值的粒子群优化算法，改进后的算法不但改善了求解的精度，而且也能够提高求解的速度.姜建国等[7]采用余弦函数对惯性权重进行非线性调整，提高了算法的搜索效率，能够有效地改善早熟现象.Clerc等[8]将压缩因子加入到算法速度更新公式当中，从而提高算法的收敛性能.文献[9]提出了一种只有位置更新公式的简化粒子群优化算法，并证明了改进算法的收敛性，算法变得更加简单高效.Deep等[10]通过利用个体最优位置和全局最优位置的线性组合来修正速度公式中的个体最优位置和全局最优位置，使算法的收敛速度和全局收敛能力得到提高.

本文结合对上述改进粒子群优化算法的分析以及文献[7、9、10]中算法的改进思想，提出了一种动态调整惯性权重的简化均值粒子群优化算法.为了进一步平衡算法的全局和局部搜索能力，惯性权重在满足非线性递减策略的基础上，加入贝塔分布的随机调整策略.同时，在简化粒子群优化算法的基础上，分别用个体最优位置和全局最优位置的线性组合取代算法速度公式中的个体最优位置和全局最优位置，从而提高算法的收敛速度以及全局收敛性能.并将本文改进的算法与线性递减惯性权重粒子群优化算法(LPSO)[11]、均值粒子群优化算法(MPSO)、简化粒子群优化算法(SPSO)以及新近或相关改进算法进行对比实验，证明了本文新算法的有效性.

2 粒子群优化算法

粒子群优化算法是对群体捕食行为进行模拟的数学模型.该算法的具体数学描述为：假设目标搜索空间的维数为D，粒子种群规模为N，Xi=(xi1，xi2，…，xiD)表示第i个粒子在D维搜索空间中的位置，Vi=(vi1，vi2，…，viD)表示第i个粒子的速度，其中i=1，…，N.pbest表示第i个粒子自身经历过的最优位置，gbest表示整个群体经历过的最优位置.在算法的整个进化过程当中，每个粒子通过不断更新pbest和gbest来更新自身的速度和位置，从而寻找到达到最优适应度值时粒子的最佳位置，即为待优化问题的解[12].粒子的速度和位置更新公式为：

(1)

(2)

其中w为惯性权重；c1和c2为学习因子，通常取值为2；r1和r2为分布在[0，1]内的随机数；t为粒子当前的迭代次数.

3 贝塔分布

贝塔分布(Beta Distribution)是指一组定义在(0，1)区间的连续概率分布，它又作为多元统计分析中一类重要的基础分布，在数理统计学等领域具有广泛的应用.贝塔分布的概率密度函数的表达式为：

(3)

式(3)中的分母是贝塔函数，其表达式为：

(4)

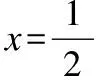
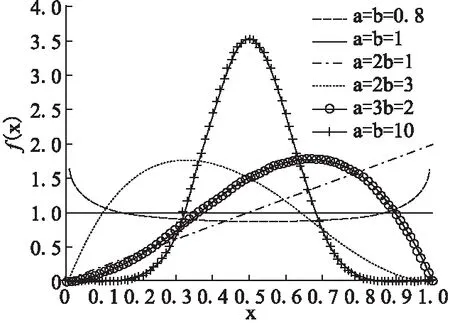
图1 贝塔分布概率密度函数图像Fig.1 Image of the Beta density distribution

4 改进的粒子群优化算法

4.1 简化粒子群优化算法

文献[9]在标准粒子群优化算法的基础上，通过去除算法中粒子的速度项，提出了一种简化粒子群优化算法(SPSO)，算法位置更新公式如式(5)所示：

(5)

简化粒子群优化算法能够在仅有粒子位置项的情况下进行迭代，使优化方程从二阶变为一阶，算法变得更简单高效，从而避免了由速度引起的粒子发散造成的算法在搜索后期收敛速度变慢等不足[9].

4.2 改进的简化粒子群优化算法

为了加快粒子群优化算法的收敛速度，且避免出现早熟现象，结合文献[10]提出的均值粒子群算法的思想，本文在简化粒子群优化算法的基础上利用线性组合(pbest+gbest)/2和(pbest-gbest)/2取代式(5)中的Pbest和gbest，因此式(5)可变为：

(6)

其中式(6)右边的第二项可以引导粒子由当前位置向粒子个体最优位置和全局最优位置的平均位置方向偏移；第三项可以引导粒子由当前位置向粒子个体最优位置方向和全局最优位置负方向的平均位置方向偏移[13].

在简化粒子群优化算法的基础上，利用个体最优位置和全局最优位置的线性组合取代位置更新公式当中的粒子个体自身最优位置部分和群体全局最优位置部分，这种改进策略充分利用了粒子自身和全局位置的有用信息，可以更好地调整粒子飞行方向与当前最好位置方向的偏移，使粒子更快地寻找到全局最优位置，从而有效地避免算法早熟收敛的问题.

4.3 动态惯性权重

从改进的简化粒子群优化算法模型中的式(6)可以看出，惯性权重依旧是平衡算法全局和局部搜索能力的重要参数之一.姜建国等[7]采用余弦函数来控制惯性权值的变化，提出一种动态改变惯性权重的策略，惯性权重变化公式可表示为：

w=[(wmax-wmin)/2]cos(πt/Tmax)+(wmax+wmin)/2

(7)

其中wmax，wmin分别为惯性权重的最大值和最小值，Tmax为粒子最大迭代次数.

上述惯性权重的改进策略为非线性地减小w的取值，改进的算法在一定程度上不仅可以提高算法的搜索效率，同时还能够改善早熟问题.由式(7)可知，虽然改进的惯性权重策略可以提高算法的寻优性能，但是在算法搜索后期，种群中的粒子都向最优解方向靠近，群体的多样性也会逐渐缺失，这样就会导致算法在搜索后期的收敛速度明显变慢[14].针对上述问题，本文借鉴文献[7，15]中对惯性权重的改进思想，提出一种动态调整惯性权重的策略，惯性权重的具体表达式为：

w=wmin+(wmax-wmin)×cos(πt/2Tmax)+σ×betarnd(a，b)

(8)

其中σ为惯性调整因子，betarnd生成服从贝塔分布的随机数，且贝塔分布能够拟合出均匀分布、正态分布等多种分布形式[16].惯性权重w表达式中的第一项和第二项通过余弦函数的改变，使得惯性权重的取值区间为[0.4，0.9]，相关实验表明，在此区间变化的惯性权值，算法能够取得较好的寻优性能[11].第三项利用贝塔分布调整惯性权重整体取值的分布，并在betarnd前加入惯性调整因子，控制w的偏离程度，从而使得对惯性权重取值的调整更加合理.

由式(8)可知，这种改进方式使得惯性权重在总体上呈非线性变化，且满足在整个搜索过程当中惯性权值递减的要求；同时再加入服从贝塔分布的随机调整策略，一方面在搜索初期惯性权值减小过快时，可能产生较大的调整值，增强算法在搜索初期的全局搜索能力，并增加粒子种群的多样性；另一方面，在搜索后期能够有机会获得较大的惯性权值，从而提高算法的搜索精度.

综合4.1-4.3小节所述，本文提出了一种动态调整惯性权重的简化均值粒子群优化算法(A Simplified Mean Particle Swarm Optimization Algorithm with Dynamic Adjustment of Inertia Weight，DSMPSO)，该算法的具体步骤为：

Step1. 参数初始化：初始化粒子数量，最大迭代次数等，并随机初始化每个粒子的位置以及粒子的速度；

Step2. 根据给定的目标函数计算所有粒子的适应度值；

Step3. 比较群体中所有粒子的适应度值与其经历过的最优位置的适应度值的优劣，如果前者更优，则用粒子的当前位置替代粒子的个体历史最优位置；

Step4. 比较群体中所有粒子的适应度值与整个群体经历过的最优位置的适应度值的优劣，如果前者更优，则更新全局最优位置；

Step5. 利用公式(6)和公式(8)更新每个粒子的位置；

Step6. 判断是否达到实验设置的终止条件，若达到，则算法停止并输出最优值；否则转至Step 2.

5 实验结果及分析

5.1 基本测试函数

为了测试本文提出的DSMPSO算法的有效性，本文选取12个测试函数[14，17]与线性递减惯性权重粒子群优化算法(LPSO)、均值粒子群优化算法(MPSO)和简化粒子群优化算法(SPSO)进行对比实验测试.12个测试函数的数学表达式如下：

(1)Sphere函数

(2)Schwefel′s P2.21函数

f2(x)=max{|xi|，1≤i≤n}

(3)Schwefel′s P2.22函数

(4) Step函数

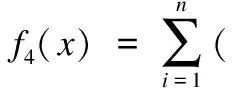
(5) Schaffers函数

(6) Rastrigin函数

(7) Griewank函数

(8) Ackely函数

(9) Schaffer函数

(10) Branin函数

(11) Six-Hump Camel-back函数

(12) Goldstein-price函数

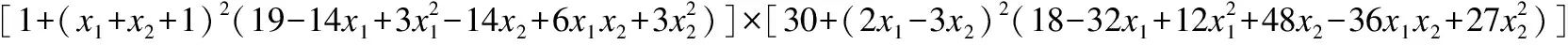
其中在12个测试函数当中，f1-f9的理论最优值都为0，f10、f11和f12的理论最优值分别为：0.3979、-1.0316、3.

5.2 仿真实验结果分析

在实验中不同的PSO算法设置了相同的群体规模N=40，最大迭代次数为Tmax=500，学习因子c1=c2=2，其他参数设置与原文献保持一致，在DSMPSO算法中：wmin=0.9、wmin=0.4、σ=0.1；在betarnd(a，b)函数中：a=1、b=2.

为了测试算法的性能，实验分为两组，算法中的维数分别设置为30和50，4种算法分别独立运行50次，各个算法在平均值(MEAN)和标准差(STD)上的比较结果如表1、表2和表3所示.图2给出了部分测试函数的适应度值曲线.其中f9-f12为2维的测试函数，实验最好结果用粗体表示.

表1 4种算法的测试结果(D=2)Table 1 Experimental results of four algorithms (D=2)

由表1的实验结果可知，对于f11-f12这2个2维函数来说，4种算法都能够寻找到理论最优值，这说明算法的寻优精度无差别.但是对于病态复杂的、很难找到理论最优值的Schaffer函数来说，DSMPSO和SPSO算法都能够寻找到理论最优值.从2维测试函数的对比结果可知，DSMPSO算法的寻优性能优势并不明显.

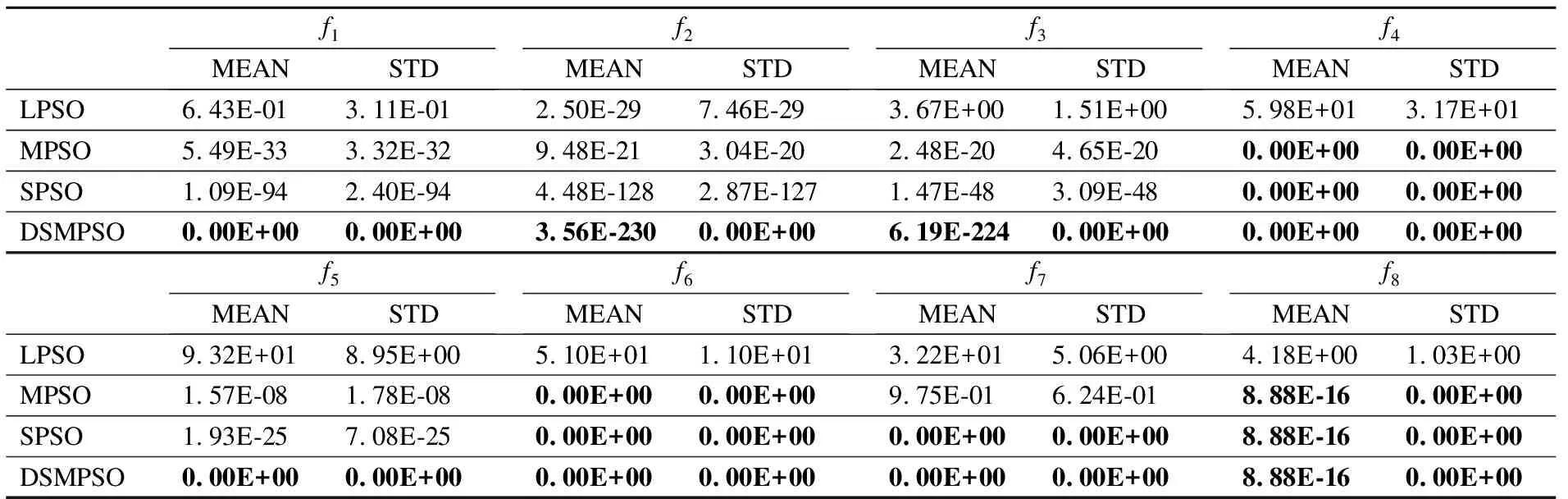
表2 4种算法的测试结果(D=30)Table 2 Experimental results of four algorithms (D=30)

为了进一步比较算法寻优性能的差异，对f1-f8这8个可变维的测试函数在不同的维数下进行对比实验.从表2和表3的对比结果可以得到，DSMPSO算法在8个测试函数上，不管是30维还是50维，DSMPSO算法与其他三种改进的PSO算法相比，对测试函数的优化效果都有进一步的提高.对于单峰问题f1-f3以及多峰问题f5，DSMPSO 算法的平均值均小于其他三种算法，说明本文算法具有更好的寻优精度.尤其是对于一般用来测试算法收敛速度的单峰函数f1和f4来说，DSMPSO算法都能够寻找到理论最优解0，并且由图2(a)、图2(e)可以看出，DSMPSO算法只需要较少的迭代次数就可以收敛到最优解.同时对于非线性多峰函数f6-f8来说，MPSO、SPSO和DSMPSO这三种算法在函数f6和f8上达到了相同的寻优精度，且SPSO和DSMPSO这两种算法在函数f6-f7上都能够寻找到理论最优解0，但是由图2可以看出，DSMPSO算法需要的迭代次数更少，因此具有更快的收敛速度.从表2和表3的结果也可以看出，DSMPSO算法的标准差均小于其他三种算法，因此算法具有更好的稳定性.由此可得，DSMPSO算法与其他三种算法相比，不管是在单峰或者多峰函数问题上(尤其是维数较高的测试函数问题)，本文改进的算法都能够具有很高的寻优精度和很快的收敛速度.

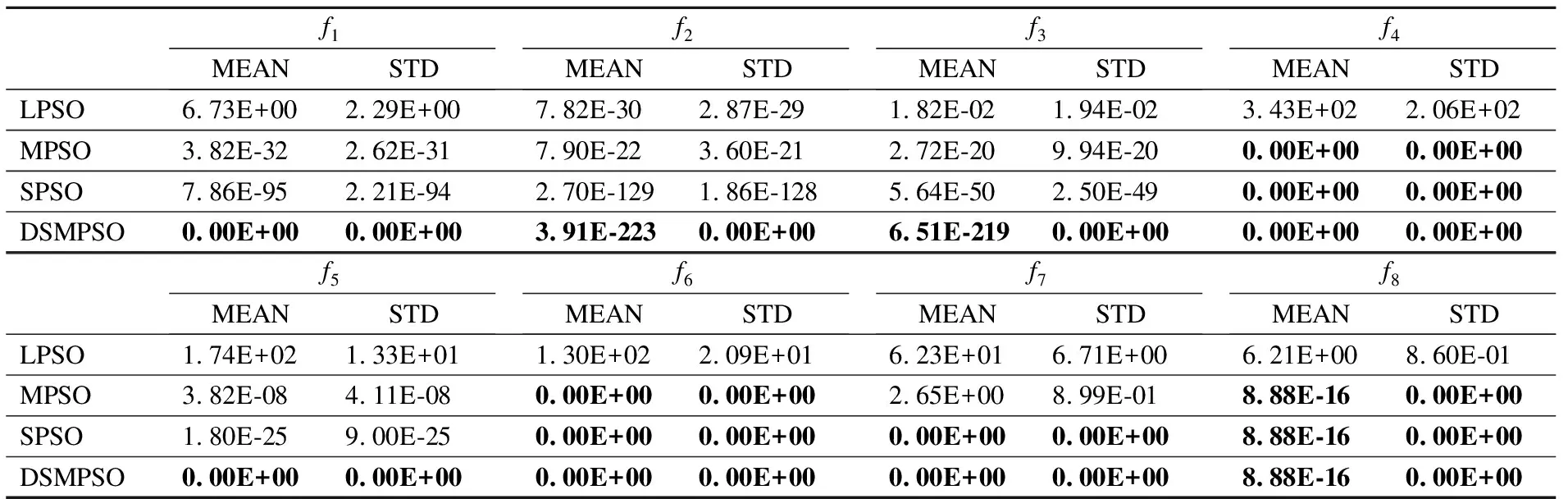
表3 4种算法的测试结果(D=50)Table 3 Experimental results of four algorithms (D=50)

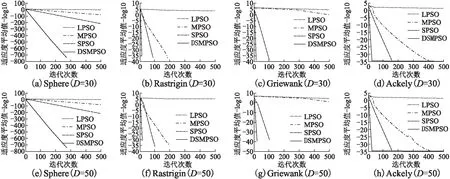
图2 不同测试函数在不同维数下的收敛曲线Fig.2 Convergence curves of different test functions under different dimensions

5.3 T检验和Friendman检验

由表1、表2和表3可知，SPSO和DSMPSO算法在12个测试函数上有8个测试函数的寻优精度相同，为了进一步明确算法之间是否存在显著性差异，本文从统计学角度来讨论算法的性能，引入T检验[18]和Friendman检验[19]，对4种算法在12个测试函数上的性能进行测试，实验结果见表4.T检验结果表明，LPSO算法与DSMPSO算法性能差异明显；DSMPSO与MPSO算法相比，在7个测试函数上的性能更优，4个无差异，1个更差；DSMPSO与SPSO算法相比，4个函数更优，6个无差异，2个更差.由Friendman检验可知算法性能越好则秩均值越小.由4种算法的Friendman检验结果可得，DSMPSO算法的秩均值最小，在4种算法中性能最好.综合两种检验结果可知，DSMPSO算法的性能比其他三种算法更优.其中“+”表示DSMPSO算法优于其他算法，“=”表示算法之间无明显差异，“-”表示劣于其他算法，w/t/l分别表示这三种比较结果的统计数目.

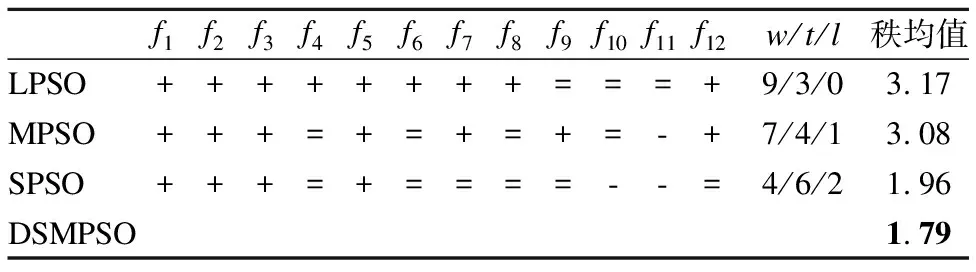
表4 4种算法的T检验和Friendman检验结果Table 4 Results of T test and Friendman test for four algorithms

5.4 指定精度下的平均迭代次数

由5.2小节的实验结果可知，表2和表3给出了在指定迭代次数下，算法寻优精度的实验结果比较.为了全面分析算法的性能，本小节给出了4种算法对8个测试函数(f1-f8)在指定精度10-10下进行测试，维数为30，各个算法分别独立运行50次的平均迭代次数如表5所示.

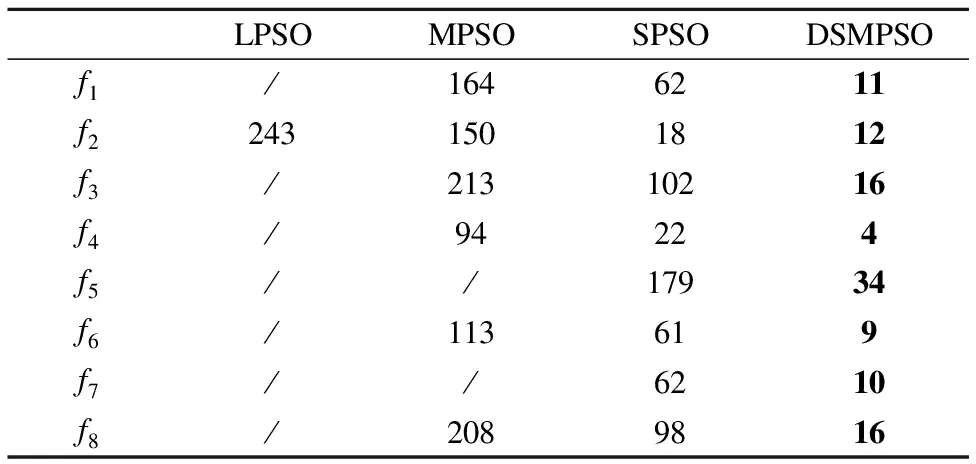
表5 指定精度下的平均迭代次数Table 5 Average number of iterations under the specified accuracy

由表5的实验结果可知，LPSO算法只在一个测试函数上达到指定精度，MPSO算法在8个函数上有6个达到指定精度，而SPSO和DSMPSO算法在所有测试函数上都达到了指定精度.并且与其他三种算法相比，DSMPSO算法都能够以最少的迭代次数达到指定精度，平均迭代次数在4-34之间，这表明DSMPSO算法的收敛速度优势明显，具有较高的寻优性能，从而也进一步说明了改进的简化均值粒子群优化算法具有收敛速度快的特性.

5.5 与新近或相关改进算法的对比实验

为了整体综合比较DSMPSO算法的性能，本文与新近相关改进的算法做了两组对比实验.实验1：与新近相关改进的粒子群算法(基于随机惯性权重的简化粒子群优化算法，SIWSPSO)[15]的比较；实验2：与新近其他两种改进的人工智能算法(动态调整惯性权重的自适应蝙蝠算法(DAWBA)[14]和自扰动人工蜂群算法(IGABC)[17])的比较.

5.5.1 与SIWSPSO算法比较

DSMPSO和SIWSPSO算法在文献[15]中的六个测试函上进行测试，两种算法的最大迭代次数为Tmax=500，维数D=30，其他参数设置与原文献保持一致，算法独立运行50次取最优值平均值(MEAN)，达到最优值的平均迭代次数(AI)作为最终比较结果，具体结果如表6所示.

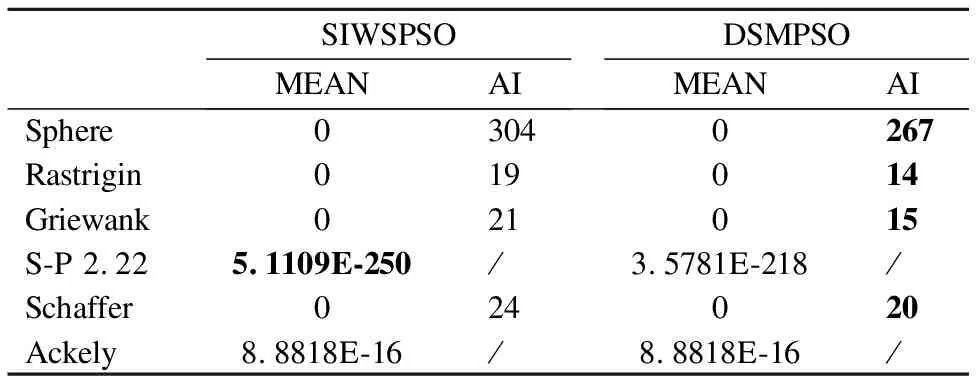
表6 SIWSPSO与DSMPSO算法实验结果Table 6 Experimental results of SIWSPSO and DSMPSO

由表6可知，两种算法在5个测试函数上的寻优精度相同，1个测试函数上的寻优精度略低于SIWSPSO算法.且在4个函数上都找到了理论最优值，同时DSMPSO算法在这4个测试函数上收敛到理论最优值的平均迭代次数明显少于SIWSPSO算法，这也说明 DSMPSO算法具有收敛速度快的优势.

5.5.2 与DAWBA和IGABC算法比较

DSMPSO与DAWBA和IGABC算法在其所测试的函数上选取五个常用测试函数，与DAWBA算法在最优值和平均值上作对比，与IGABC算法在最优值平均值和标准差上作对比，DAWBA和IGABC算法的实验数据结果均来自原文献，具体比较结果见表7和表8.

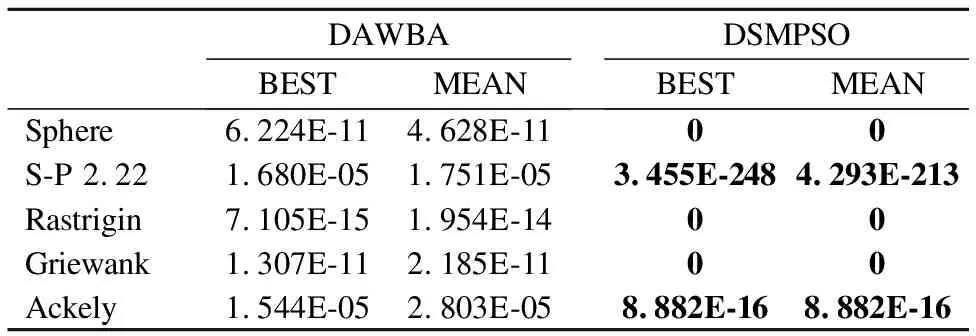
表7 DAWBA和DSMPSO算法实验结果Table 7 Experimental results of DAWBA and DSMPSO

由表7的实验结果可得，DSMPSO算法的寻优精度均优于与DAWBA算法，说明本文算法的寻优精度高.由表8可知，两种算法在函数Rastrigin和Griewank上的寻优性能相同，在其他3个测试函数上的寻优结果优于IGABC算法.

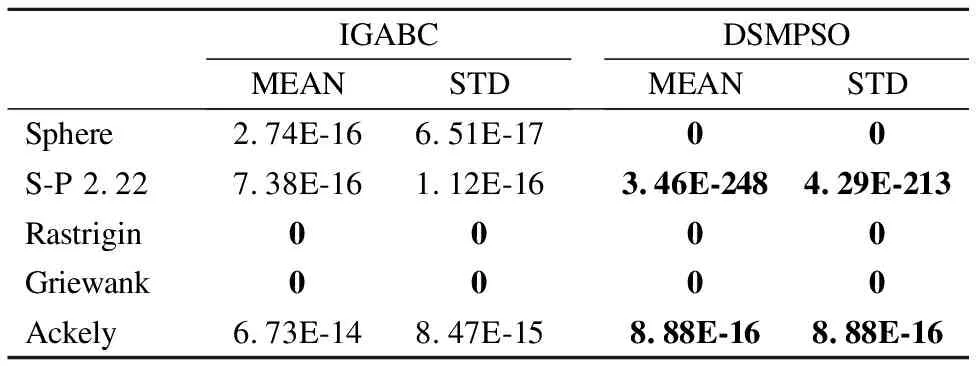
表8 IGABC 和DSMPSO算法实验结果Table 8 Experimental results of DAWBA and DSMPSO

综合上述2组对比实验结果可知，不管是与新近的相关改进粒子群算法相比，还是与其他新近的人工智能算法相比，DSMPSO算法都具有良好的寻优优势.

6 结 论

本文在简化粒子群优化算法的基础上，提出一种动态调整惯性权重的简化均值粒子群优化算法.通过对算法速度公式中个体最优位置和全局最优位置的修正，以及对惯性权重加入贝塔分布的动态调整，既增加了种群的多样性，又使得算法具有良好的全局收敛能力.仿真实验结果表明，本文改进的算法具有较快的收敛速度，以及较高的寻优精度.同时改进的算法对解决维数较高的多峰函数问题，具有良好的性能和潜在的应用价值.