三元概念分析的联盟应用研究
2019-01-24王红敏王黎明
王红敏,张 卓,王黎明
(郑州大学 信息工程学院,郑州 450001)
1 引 言
随着网络技术的飞速发展,互联网中涌现出了越来越多的三维数据.1995年,Wille R.等受实用主义哲学的启发把FCA(形式概念分析)扩展到三元背景下,提出了三元概念分析.Lehmann.和Wille 在文献[1]中首次定义了三元背景、三元概念和概念三元格.文献[2]介绍了如何从三元图中读出不同的信息.文献[3]提出了一种构造三支概念的算法CbO3C.文献[4]介绍了三支概念与经典形式概念的关系,并且在经典形式背景给出了两种具体的三支概念模型.文献[5]从三支决策的视野探究不同概念格之间的内在联系.文献[6]梳理了三元概念分析的研究现状及发展趋势.文献[7]研究了概念三元格的构造算法及其在folksonomy分类中的应用.文献[8]研究了三元概念分析在文本分类中的应用.
关于经典的合作博弈,已经存在诸多相关研究并且广泛的应用在多智能体协作[9,10-12]等领域.合作博弈的第一个主要问题是参与者如何结盟.然而,在大多数情况下,并不是N的所有子集都可以构成一个联盟或者是可行的,这就意味着效用函数只是映射在2N的子集F上.Aumann和Dreze[13]针对该情况提出了联盟结构.Faigle和Kern[15]提出了限制合作.F在分布格(在交和并下封闭)[15]、凸代数[16]等一些结构的假设中被研究.与以往研究不同的是,本文基于参与者所拥有的资源,提出受限合作博弈,在这种条件下,经典的Shapley值将不再适用,需要重新定义.2014年,Faigle U[17]等人提出了基于概念格的博弈,但他只是从数学层面给出了一些定理,并没有指出相关的应用以及算法的实现.因此本文借鉴形式概念分析上的博弈以及结合作为处理分析数据新框架的三元概念分析的特点,提出了受限合作博弈,并且结合三元概念分析与合作博弈的特点,提出了受限合作博弈的联盟形式的形成算法LMXC,以及效用值分配G-shapley值法.
2 相关理论
2.1 三元概念分析基本理论
三元概念分析作为形式概念分析的推广,是一种新的信息处理的概念和计算范式,它能够有效的处理三维数据.网络上的三维数据可以表示为三维二值表,根据相应算子的计算推理,进而得到所有的三元概念.
定义1.[6](三元背景):三元背景被定义为四元组(G,M,B,Y),其中G是对象集合,M是属性集合,B是条件集合,Y是G、M和B之间的三元关系,且Y⊆G×M×B,(g,m,b)∈Y表示对象在条件b下具有属性m.
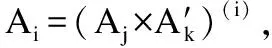
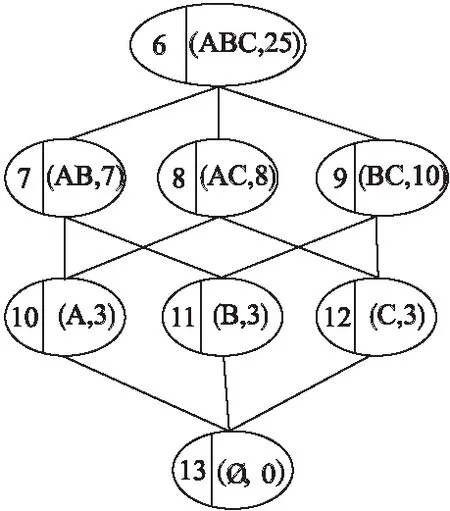
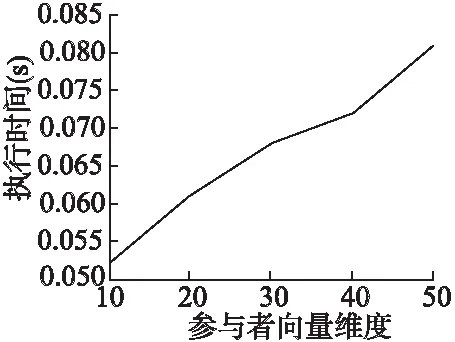
定义3.[6]((i)-诱导算子):三元背景K=(K1,K2,K3,Y),{i,j,K}={1,2,3},满足j X→X(i):={(aj,ak)∈Kj×Kk|(ai,aj,ak)∈Y,∀ai∈X} Z→Z(i):={ai∈Ki|(ai,aj,ak)∈Y,∀(aj,ak)∈Z} 定义4.(预序和等价关系):三元背景K=(K1,K2,K3,Y),S为三元背景下所有三元概念的集合,对于任意的(A1,A2,A3)∈S,(B1,B2,B3)∈S,定义预序关系≤i和等价关系~i为: (A1,A2,A3)≤i(B1,B2,B3) Ai⊆ Bi, (A1,A2,A3)~i(B1,B2,B3) Ai= Bi, i={1,2,3}. 用N={1,…,n}表示有限个参与者的集合,在这n人的博弈中,N的任何一个子集S就作为一个联盟,与结盟相关的是特征函数.空集Φ和全集N也可以称作联盟,单点集{i}仍是一个联盟.然而,在多数情况下,合作是受限的,比如当只有他人加入到此联盟时一些人才加入该联盟.本文我们考虑一般情况,即合作是受限的. 一个合作博弈(F,ν),对于任意一个S⊂N的联盟,一个分配向量就是一个向量x∈Rn,对每个参与人i∈N分配一个实值参数,形成n维向量x={ x1,…,xn}. 本文首先利用三元概念分析的理论解决受限合作博弈联盟形式形成问题,然后结合三元概念分析与Shapley值法提出G-shapley值法,进而能够有效分配联盟的效用值,得到每个参与者的平均边际贡献. 针对联盟的形成问题,经典的合作博弈理论假设N局中人任意的子集都成为一个联盟,比如,有N={A,B,C}三个参与者,那么依据其理论,就形成B={Φ,A,B,C,AB,AC,BC,ABC}八种联盟形式.然而,实际的很多情况下,参与者并不是一成不变的,即参与者所拥有的资源与它所处的条件息息相关,就比如,参与者A在a条件下有资源1,随着环境的变化,参与者在条件b下就不一定还拥有资源1,因此,参与者的个体状况依赖于它所处的环境.针对此种情况,本文结合三元概念分析与合作博弈各自的优势提出一种新的理论,称之为受限合作博弈这种合作方式仍然有一定的联盟优势.类似于合作博弈联盟的概念,本文提出如下联盟形式的概念: 定义5.(联盟形式)联盟形式以三元组(A,B,C)的形式刻画,A代表参与者集合,B表示参与者在条件C下共同拥有的资源集,C表示条件集合. 为有效处理受限合作博弈的联盟形式形成问题,同时为了清晰描述本文理论,本节借鉴Faigle U[17]提出的基于概念格的博弈论,并结合三元概念分析的特点,以提出问题并解答问题的方式解析联盟形式的形成过程. 为解决上述问题,首先将上述条件通过三元背景的形式进行描述,利用三元背景的对象集K1代表参与者的集合、属性集K2代表参与者所拥有的资源或能力、条件集K3表示参与者所属条件的集合.如果参与者在某个条件下具有某种资源或者能力,在相应的位置上就用1表示,否则用0表示,最终通过三元背景描述了参与者、参与者在特定条件下所拥有的资源、参与者所属的条件之间的三元关系.联盟形式的形成借鉴了文献[18]的CTLA算法的思想,具体的形成过程主要包括两部分:一:在单个条件下,类似于合作博弈理论中,单点集{i}也称为联盟,本文将单个参与者依靠自身所拥有的所有资源或能力也看作一种联盟形式,多个参与者为形成强强联合,提高效率,依赖他们共同拥有的资源组成多参与者合作的联盟形式,基于此就形成了单个条件下所有的联盟形式.二:在多个条件下,有时参与者在不同的条件下具有某些同种类的资源,为了使本文研究粒度更加细化同时为了对后续联盟效益分配更加精确,针对此种情况将某些条件下参与者共同拥有某些资源也看作一种联盟形式,有时还表示在不同的条件下存在相同参与者及同种资源的合作方式,为了减少冗余,将条件进行合并. 定义6.(稳定联盟):如果一个联盟是任一三元概念的外延,那么这个联盟是有效的或者说是稳定的.在相同的条件下(S′′,S′)是一个二元概念,形成的联盟也是稳定的. 定义7.(受限合作博弈):受限合作的博弈是一个三元组T=(N,F,ν),N是有限个参与者的集合,F是N的子集构成的有效联盟的集合,ν是F→R的效用值函数,并且ν(Φ)=0. 算法1.LMXC() 输入:预处理后的三元背景(K1,K2,K3,Y) 输出:所有的联盟形式C 1.begin 2. for(every a∈K3) 3. 在模式a下所有的联盟形式以概念的形式存入f[a] 4. for(every(S,S′)∈f[a] 5. (S,S′)→(S,S′,a) 6. end for 7. end for 8. e=|K3|; 9. for(int i=0;i 10. for(every(A1,B1,C1)∈f[i]) 11. for(every(A2,B2,C2)∈f[i]) 12. if(A1=A2and B1=B2) 13. Insert((A1,B1,C1∪C2)) 14. end if 15. end for 16. end for 17. end for 18.end 算法2到5行,描述在单个条件下,如果不同的参与者拥有相同的能力技能,为了实现强强联合,获得更多的利益,就形成该条件下的联盟形式.单个参与者也可不与其他参与者合作,仅使用自身所有能力形成类似于单点集的联盟形式. 基于ARIMA-TREND的企业价值评估收益法探析——以A企业价值评估为例 …………… 李保婵 王思颖 林俊良(4/36) 算法10到13行,算法10到16行,描述在不同的条件下,如果得到相同的参与者组合及相同的资源集组合,就说明此参与者组合存在不同条件下的合作,为提高效率对不同的条件进行合并以及为了使联盟效益分配更加合理同时使研究粒度更加细化将参与者在不同条件下共同拥有的属性此种状态也刻画为联盟形式. 为了使上述的联盟形式的形成更加清晰、直观,接下来引入一个算例,将该理论用在企业之间的合作. 算法实例1.在2012年在接受访问的14家通州企业中,有12家与其他企业有合作,以其中三家企业为应用背景,结合企业的行业特点,综合国内外有关企业能力评价指标已有的结果,建立了企业能力指标体系及其指标量化结果如表1所示,表1列举了3家企业构成的集合为N={A,B,C},a、b、c、d分别代表技术、生产、销售、资金四种合作方式,1、2、3、4、5、6分别表示企业在技术力量、售后服务、资产负债、地理位置、市场影响、企业信誉六个方面的能力,用本节提出的联盟形式的形成理论,依据企业所拥有的能力可以形成哪些联盟形式. 首先用三元形式背景来刻画上述问题,如表1所示. 表1 三元背景 abcd123456123456123456123456A111111111B111111111C111111111111111 针对上述问题,根据LMXC算法生成以下联盟形式:(A,146,d),(AC,126,c)(A,15,a),(B,146,b),(C,12356,b),(BC,16,ab),(C,1246,a),(C,126,abc),(ABC,1,abcd),(B,15,cd),(AC,16,cd),(C,16,abcd),(C,136,bd). 在上述的结果中,通过LMXC算法共生成了13个联盟形式,将联盟形式以三元组的形式表示,分别代表企业组合、企业组合共有的技能、合作模式.根据定义2的三元概念的形成理论可知每个联盟形式都是一个三元概念,因此这些联盟形式又是稳定联盟,每个稳定联盟中的局中人,这里表示每家企业受外界约束不会随意退出该联盟.每个三元概念代表一定的合作含义比如概念(AC,126,c)就表示企业A和C在技术力量、售后服务、市场影响三方面较一致,进行销售合作.企业也有可能不进行合作,(C,136,bd)就表示企业C依靠自身所拥有的技术力量、资产负债情况、企业信誉独自完成生产与资金模式.每个联盟形式又是稳定的,比如企业A拥有能力126可以独自完成生产模式.但为了形成更加稳定的联盟以获得更多的利益,它会与拥有同样能力的企业C合作. 如果运用经典的合作博弈理论针对上述的三家企业的合作问题,它不考虑企业合作模式的种类的状况以及企业在不同的合作模式下所拥有资源的变化情况,只是简单的用穷举的方法产生{Ø,A,B,C.AB,AC,BC,ABC}所有这8种联盟形式,如果有N家企业,那么也将用穷举的方法生成2N种联盟.显然,本文提出的联盟形式形成算法与经典的合作博弈联盟形成方法相比在粒度上更加细化,不仅考虑到参与者自身拥有的资源状况还充分的考虑到了参与者所处的条件. 效用理论的核心是效用和效用函数,每个联盟形式的形成都对应一个效用值,效用值由特征函数描述.将联盟的效用值进行合理的分配,这是联盟稳定的关键因素之一.博弈论Shapley值基于参与人的边际贡献来对参与者进行分配,比其它的方法公平.因此本文以经典Shapley值为基础,又因为本文讨论的是受限合作博弈,即特定条件下的合作,那么Shapley值将不在适用.基于此本文将经典的Shapley与三元概念分析相结合提出了G-shapley值法. 定义9.(G-shapley):对于每一个三元博弈(l,V)存在唯一的G-shapley值:Φ(v)={φ1(v),φ2(v),…,φn(v)}.其中: Φi((l,V))= (1) 基于G-shapley的特性,可以在条件维上定义G-shapley,依据G-shapley值的最终结果可以对条件的重要程度进行排序和加权.还可以在属性维上定义G-shapley值,这样能够有效的依据其结果对参与者所拥有的属性的依赖程度进行由经典形式背景向模糊形式背景的转化. 定义9.(同伴参与者):F是N上的一个闭系统[17].一个子集K⊆N,对于任意一个不为空的子集S∈F,如果K⊆S或者K∩S=Φ,那么|K|>1在F上是一个同伴参与者. 定理.l=(K1,K2,K3,Y)是一个三元背景,(l,v)是三元背景l上的博弈,如果K是联盟S同伴参与者,那么Φi(l,v)=Φj(l,v). 基于上述定理可以在属性上定义同伴参与者,当两个属性满足同伴关系时,可以有效的进行属性消减. 算法2.G-shapley值法: 输入:联盟形式集合T、概念子节点数组S 输出:成员利益分配D //判断叶子节点和根节点是否唯一,修正概念集 1. for each c∈S 2. if S[c].size==0 3. Leaf.add(c) 4. else 5. Unroot.put(S[c]) 6. end if 7. end for 8. if Leaf.size > 1 9. c1 = createConcept(Leaf) 10. T.add(c1) 11. LeafNode = c1 12. else 13. LeafNode = L[0] 14. end if 15. if (T.size - Unroot.size)> 1 16. c2 = createConcept(Root) 17. T.add(c2) 18. end if 19. //重新计算联盟间关系 20. S′ = computeRealtion(T) 21. //从叶子节点出发向上,递归得到所有链路 22. Links = constructLinks(T,S′,LeafNode) 23. //根据链路计算联盟成员收益 24. for each p∈RootNode.Extends 25. for each r∈Links 26. for each c∈r 27. c′ = r[c+1] 28. if !c.Extends.contains(p)& 29. c′.Extends.contains(p) 30. profit +=(P[c′] P[c])/ 31. (c′.Extends.size-c.Extends.size) 32. end if 33. end for 34. end for 35. D[p]= profit 36. end for 37. Output D 算法第1行到19行,根据A1⊆B1、A2⊇B2及A3⊆B3对所有的联盟形式进行联盟形式格结构的构造. 算法第20行到35行,求解参与者i的能力值.如果参与者i属于拥有全部资源的联盟,对该联盟值均分,否则,搜索整个格结构的每条链,查找任一条链第一个包含i的联盟形式,以及最后一个不包含链的联盟形式,得到参与者i的平均边际贡献. 为了验证本节提出的G-shapley值的正确性,引用文献[19]中的背景数据,该文献将Shapley值应用在在农产品合作供应链中,符合本文的研究理论,本文用到的具体数据如图1所示. 图1 联盟形式格结构图1 Lattice structure of alliance form 在农产品合作供应链中有三个参与者,它们分别是:生产者A、物流商B、零售商C,当A、B、C单独经营时,均能获得3万元的收益,若A和B合作获7万元,A和C合作获8万元、B和C合作获10万元,A和B和C合作获10万元. 依据上述数据,采用本文提出的G-shapley值法计算三个参与者的分配利益,农产品合作供应链可看作单个条件下的合作问题,根据G-shapley值法的主要思想,形成图1所示的联盟形式格结构: 图中的每个节点由联盟形式及其对应的效用值的有序对组成,按上述联盟形式的定义,联盟形式应有参与者组合,共同的资源及条件组合这三部门组成,但此处解决的是单条件在的利益分配问题,为描述简单又由于文献[19]未详细描述参与者的资源信息,因此联盟形式用参与者集合描述.图2共有6条链路组成: 第1条链路:8 5 2 1 第2条链路:8 5 3 1 第3条链路:8 6 2 1 第4条链路:8 6 4 1 第5条链路:8 7 3 1 第6条链路:8 7 4 1 求解生产者的分配利益ΦA(v)具体过程: 1.在第1条链路上找到最后一个不含生产者A的联盟形式并获得它的效用值,由图2可知它为节点8,节点8的联盟形式是∅,效用值为0; 2.在第1条链上找到第一个含有参与者A的联盟形式并获得它的效用值,由图2可知它为节点5,节点5的联盟形式为A,效用值为3. 3.计算联盟形式A与联盟形式∅参与者差值的模|A∅|=1. 同理可得物流商分配利益ΦB(v)=8.5万元;零售商分配利益ΦC(v)=9万元.与文献[19]中通过经典Shapley值计算的结果是一样的,具体的计算过程文献[19]已展示,这里不再赘述. 本文提出的G-shapley值适合任何使用经典Shapley值计算利益分配问题,但如果是多条件下的利益分配问题,就不能再使用经典Shapley值计算. 本文提出的模型主要包括两个部分:LMXC()算法和G-shapley()值法,对每个部分进行时间复杂度分析.LMXC()和G-shapley()的时间复杂度与三元概念中的外延、内涵和条件都有关系,LMXC()算法的执行时间主要取决于联盟形式的形成,联盟形式由参与者数量,参与者拥有的资源和条件种类共同决定,而在满足三元关系的情况下,这三者可分别看作三元背景的对象数目、属性数目和条件个数.在计算每个条件下形成联盟形式的时间复杂度时,需要考虑到所有参与者的所有资源.因此,每个条件下联盟形式的时间复杂度为O(‖L1‖*‖L2‖),那么在所有条件下形成联盟形式的时间复杂度为O(‖L1‖*‖L2‖*‖L3‖).G-shapley值法的时间复杂度取决于LMXC()算法生成的联盟形式的数量,假设由LMXC形成的联盟形式个数为‖A‖,在G-shapley的格构建过程中,在判断任意一个联盟形式与其他联盟形式的关系时,需要搜索除它以外所有的联盟形式,因此格构建的时间复杂度为O(‖A‖*‖A‖).对参与者的效用分配,需要考虑三个阶段:联盟形式的形成、联盟形式格的构建,格的搜索,在格的搜索过程中,考虑极限情况,在评估每个参与者复杂度为O(‖L1‖*‖A‖).综上所述,总的时间复杂度为:O(‖L1‖*‖L2‖*‖L3‖+‖A‖*‖A‖+‖L1‖*‖A‖) 文章的第三部分已对提出的理论进行了有效性的分析与验证,因此本节分别测试LMXC和G-shapley值法的性能,由于本文是从参与者所拥有资源层面进行受限合作研究的,与经典的合作博弈不同,由于没有权威的联盟形式形成算法以及效用分配算法作比较分析,因此本文的算法没有与其它文献的算法进行对比. 实验环境:3.4GHz CPU,4GB内存,Win10操作系统,使用Java实验平台对LMXC()算法及G-shapley值法的性能进行验证.针对本文的研究内容,由于没有典型的数据集,因此实验用到的数据是随机生成的. 实验中分别将参与者数量、参与者向量维度作为变量执行LMXC算法. 实验1.a.在参与者能力向量维度为10,条件种类为5的条件下使参与者的个数不断增加,实验结果如图2所示. 图2 实验a参与者数量作为变量实验分析图Fig.2 Performance of experiment a where as variable 实验结果表明,固定参与者能力向量维度以及条件种类的条件下,随着参与者数量的增多,运行时间也随之增加.这是因为当参与者的个数增多时,参与者的组合方式随之增加,在单个条件下形成的联盟形式也增加.在多个下进行联盟形式的合并时,需要对比的联盟形式的数量也会增加,从而导致算法的执行时间增长. b.参与者数量为30,条件种类为8的条件下,使参与者向量维度不断增加,实验结果如图3所示. 图3 实验b参与者向量维度作为变量实验分析图Fig.3 Performance of experiment b where attribute as variable 实验结果表明,随着参与者能力向量维度的增加,运行时间也随之增加.这是因为当参与者的能力向量维度增加时,参与者的合作方式种类会增加,相应的联盟形式的个数也会增长.通过图2和图3观察到,算法的执行时间都有所增加,原因是无论是增加参与者的数量还是增加参与者的向量维度,最终都会导致联盟形式的增多,从而影响算法的性能. 实验中将LMXC算法得到的联盟形式作为输入执行G-shapley值法并进行分析,通过观察该算法的运行时间来衡量算法的性能. 实验2.a.在参与者能力向量维度为6,条件种类为3的条件下,参与者个数不断增加,实验结果如图4所示. 图4 实验a G-shapley分配实验分析图Fig.4 Performance of experiment a G-shapley b.在参与者数量为30,条件种类为3的条件下,参与者向量维度不断增加,实验结果如图5所示. 图5 实验b G-Shapley分配实验分析图Fig.5 Performance of experiment b G-shapley 从图4和图5的实验结果观察到如果将LMXC的运行结果传送给G-shapley,它的运行时间随着参与者数目的增加或者参与者向量维度的增加而有所上升这是因为在求解G-shapley值的过程中,首先要构建联盟形式的格结构,随着输入的联盟形式的数量的增多,所构建的格会变大,在计算参与者的平均边际贡献时,要搜索所构建格的每条链,在每条链上查找其对应联盟形式的效用值时,每个环节都会随着联盟形式数量的增多,算法的执行时间也会增加,实验结果表明,只要联盟形式的数量增多,在执行G-shapley进行分配时所需时间就会增大. 本文在三元概念分析理论的基础上引入了受限博弈,主要研究了如何运用三元概念分析解决受限合作的联盟形成以及为了得到参与者的分配值,结合三元概念分析的理论提出了G-shapley算法,同时通过实验测试了本文模型的效率.该理论的提出是对三元概念分析的扩展,同时也为三元概念的应用奠定了基础.虽然三元概念分析有很大的发展空间,但本文提出的理论是三元概念分析在受限合作博弈上的初步探索,仍有许多不足之处,如本文提出的G-shapley值法,随着参与者人数的增多,算法的运行时间有待进一步研究以及LMXC算法也要进一步优化.2.2 合作博弈
3 三元概念分析的联盟应用
3.1 联盟形式形成
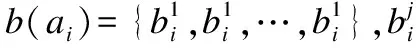
Table 1 Triadic concext
3.2 效用值的分配

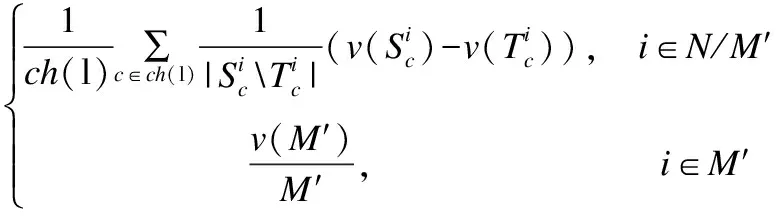
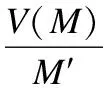


3.3 算法的时间复杂度分析
4 实验结果与分析
4.1 联盟形式构造

4.2 联盟效用分配


5 总 结
