不确定数据背景下基于DS-MM的设备健康预测研究

吴健飞，刘勤明，吕文元，叶春明

(上海理工大学 管理学院, 上海 200093)

1 引 言

随着现代化工业技术的蓬勃发展，机械设备的可靠性和维护水平已成为保证系统正常运行的必要条件.在实际生产过程中，随着设备使用时间的增加，设备的性能在不断衰退，若不进行有效的维护，设备可能会失效或者发生故障，从而会影响企业的生产效益.所以在设备的健康状态严重之前，对设备进行实时的处理，可以避免一些成本高昂的维修，降低设备的维护成本，提高设备的利用率.

设备的健康预测是有效实施维护策略的关键，由于数据监测和计算机技术的进步，关于设备健康预测理论的研究引起了国内外学者的关注[1-3].其中，基于马尔可夫链的预测方法显得尤为突出.例如：Du Ying等人将隐马尔可夫模型(HMM)应用到润滑油的寿命预测中，在该方法中，假设状态的驻留时间服从指数分布，但这与实际并不相符[4].针对HMM中的不足，许多学者又研究了基于隐半马尔可夫模型(HSMM)的预测和诊断，HSMM模型没有HMM模型中不符合实际的假设，因此对实际问题具有更强的建模和分析能力.像Akram Khaleghei将HSMM模型用于部分观测的故障系统的寿命预测中，并利用EM算法估计出HSMM中的参数[5].Dong等人使用隐半马尔可夫模型(HSMM)进行机械故障诊断和故障预测，结果表明其故障识别率比HMM提高了，且基于HSMM的剩余寿命预测模型效果也较好[6，7].Wang等人针对设备运行状态识别与故障预测问题，提出一种基于时变转移概率的隐半Markov模型，并通过滚动轴承的实验，证明了基于该模型的设备健康预测方法比传统的隐半Markov模型方法更加有效[8].

然而目前的研究大都是基于样本数据准确的情况下对设备进行的健康预测[9-12]，而关于在数据不确定情况下的设备健康预测文献较少，或在数据不确定情况下对设备进行健康预测的研究很难得到令人满意的结果[13-17].不确定数据是指在工程实际中由于噪声、扰动、非理性测量仪器以及人为等因素导致数据在产生过程中出现异常的情况.

不确定的数据会导致样本数据的不准确，不仅增加了分析数据的难度，而且会导致数据挖掘结果产生偏差，不能准确的对设备进行健康预测.因此，针对数据不确定的情况，本文基于马尔可夫模型，首先利用DS证据理论构建状态识别框架.其次，用区间数来表示不确定的数据，并利用区间数之间的距离和相似度作为产生BPA的证据，为了使预测结果更加准确，采用Pignistic概率转换将BPA转化为基础状态的概率分布.最后，通过一个案例研究验证了提出方法的有效性.

2 DS-MM理论框架

2.1 DS证据理论

设θ为一有限集，2θ为θ上的幂集，m是2θ到[0,1]上的函数，若满足：

m(φ)=0，∑A⊆2θm(A)=1

(1)

称m为θ上的基本概率分配函数，∀A∈2θ，m(A)称为A的基本概率赋值，反映了对A的信任程度.如果A的基本概率赋值m(A)>0，则把A称为θ的一个焦元.θ通常也称为识别框架，表示在条件E下所有可能结论的基础命题的有限集，θ的一个子集A，即2θ中的元素，可以理解为一个命题.

2.2 Markov链

随机序列Xn在任一时刻n，它可以处在状态O1,O2,…,ON，且它在l+k时刻所处的状态为ql+k的概率，只与它在l时刻的状态ql有关，而与l时刻以前所处状态无关，即：

P(Xl+k=ql+k|Xl=ql,X1=q1)=P(Xl+k=ql+k|Xl=ql)

(2)

其中q1,q2,…,ql,ql+k∈(O1,O2,…,ON)，则称Xn为Markov链.

并且称Pij(l,l+k)=P(ql+k=Oj|ql=Oi)为k步转移概率，其中1≤i,j≤N，l,k为正整数.当Pij(l,l+k)与l无关时，称这个Markov链为齐次Markov链，此时Pij(l,l+k)=Pij(k).当k=1时，Pij(1)表示单步转移概率，简称为转移概率.

3 基于DS-MM的设备健康预测

3.1 识别框架确立

根据相同设备的历史运行状况可以建立状态识别框架θ={θ1,θ2,…,θn}，其中θ1,θ2,…,θn表示设备的n个基础状态.识别框架θ的幂集为2θ，令2θ中的每个元素分别代表设备运行中的一个状态，则设备的状态相应的在原来的n个基础状态上增加了，然后根据实际情况可以确定每个状态对应的数据范围.

3.2 基本概率赋值计算

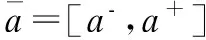
另外，若A=[a1,a2]，B=[b1,b2]分别表示两个区间数，则它们之间距离的平方为：

(3)

其中，D(A,B)表示区间数A和B之间的距离.虽然采集到的数据很多是确定的，但是仍可以用区间数来表示，例如10可以表示成[10,10].因为每个状态都有对应的数据范围，基于公式(3)，计算采集到的数据和状态之间的距离.然后基于区间数之间的距离计算区间数之间的相似度.区间数之间的相似度定义为：若X=[x1,x2]和Y=[y1,y2]分别表示两个区间数，则这两个区间数的相似度为：

(4)

最后，标准化计算出的区间数相似度就得到采集数据的基本概率赋值，具体计算过程见图1.

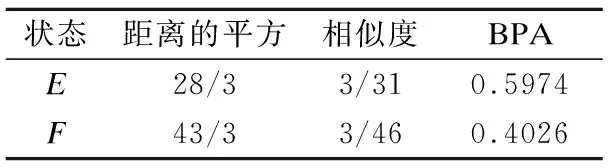
图1 基于区间数的BPA计算过程Fig.1 BPA calculation process based on interval number

通过一个例子来说明整个计算过程：若状态E对应的数据范围为[0,5]，状态F对应的数据范围为(5,10]，给定一个区间数C=[3,6]，则区间C的基本概率赋值见表1.

3.3 转移概率计算

获得每个采集数据的基本概率赋值后，计算各个状态之间的转移概率，如下：

(5)

其中m(i)t表示状态i在第t个时间点的基本概率赋值，n表示马尔可夫链的长度.所以状态转移概率矩阵P=[Pij].在这里，状态之间的转移是指识别框架中的所有状态.

3.4 健康预测计算

利用得到的状态转移概率矩阵P和采集到的最后一个时间点上数据的基本概率赋值m，可以计算出下一个时间点上数据的BPA，即：

m预测=m·P

(6)

其中m=m(i)，i∈2θ表示采集到的最后一个时间点上数据的基本概率赋值.

虽然得到了下一个时间点上数据的基本概率赋值，但有时想通过基本概率赋值直接进行预测还是不容易的.为了更准确的进行健康预测，本文采用Pignistic概率转换将识别框架中所有状态的基本概率赋值转化为基础状态的概率分布.Pignistic概率转换是为了重新分配系统已获得的各命题的信度值，以得到更可靠的决策依据.通常使用的分配方式是平均分配法，即认为每个元素出现的概率相同，因此多元素命题的BPA值被平均分配到所包含的元素中：

(7)

m(A)为A的基本概率赋值，|A|表示A中元素的个数.得到了基础状态的概率分布即可知道下一时间点设备状态.

4 案例分析

通过机械设备的健康预测来验证所提出方法的有效性.机械设备在运行使用过程中会经历不同状态的演化，假设这个演化过程服从马尔可夫过程，并且设备的状态可以用下面三个状态来表示：健康状态{0}，退化状态{1}，失效状态{2}.表2是在一段时间内通过传感器从设备上采集到的20个数据，其中在第3、6、13、16个时间时由于传感器的波动导致采集的数据是不确定的，我们用区间数来表示这些不确定的数据.

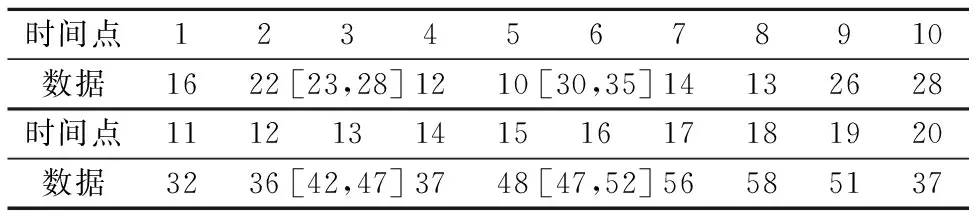
表2 一段时间内采集到的数据Table 2 Data collected over a period of time

根据相同设备的历史信息可以得到三个基础状态对应的数据范围，见表3.

表3 3个状态下对 应的数据范围Table 3 Corresponding data range in three states

4.1 DS证据理论确定状态识别框架

考虑到在某时间点采集到的数据不能表示设备以概率1处于某个状态，即数据18可能表示设备以概率0.4处于健康状态{0}，以概率0.6处于退化状态{1}.所以通过历史信息得到的3个状态的据范围并不很合理.利用DS证据理论解决该问题.

因为采集到的所有数据都可以表示设备处于3个基础状态：健康状态{0}，退化状态{1}，失效状态{2}.所以可以构建识别框架θ={0，1，2}，得到θ的子集为{0}，{1}，{2}，{0,1}，{0,2}，{1,2}，{0,1,2}，φ，在一个证据识别框架中这些子集分别代表一个状态，这些状态及对应的数据范围见表4.

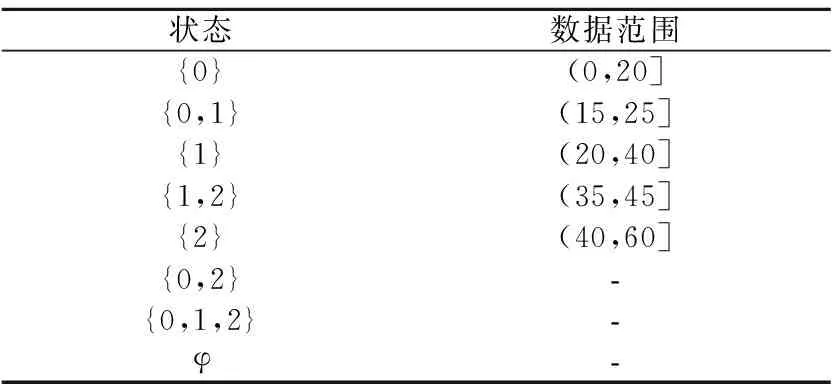
表4 识别框架中的状态及这些状态对应的数据范围Table 4 Identify the states of the frame and the range of data corresponding to those states

考虑到在实际情况中，设备不可能既处于健康状态0又处于失效状态2，所以状态{0,2}没有对应的数据范围，同理，状态{0,1,2}和φ也是.所以最后的有效状态为{0}，{0,1}，{1}，{1,2}，{2}.在状态和对应的数据范围确定之后，可以得到20个采样时间点的状态分布，见图2.

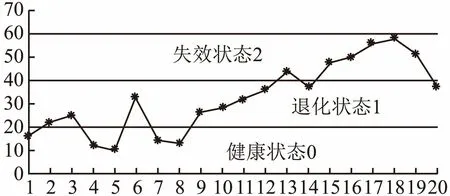
图2 20个采样数据点的状态分布Fig.2 State distribution of 20 sampling data points

4.2 计算采集数据的BPA

根据图1的计算过程，可以获得20个数据的基本概率赋值.以第6个采样时间点上的数据为例来表示计算过程.因为第6个时间点上的数据是不确定的，用区间数来表示.识别框架中有效状态对应的数据范围也用区间数的形式表示，所以第6个时间点上的数据和有效状态对应的数据范围之间的距离可以利用公式(3)计算出来；然后根据公式(4)，可以计算区间数之间的相似度；最后标准化相似度就可以得到第6个时间点上的数据的BPA.结果见表5.

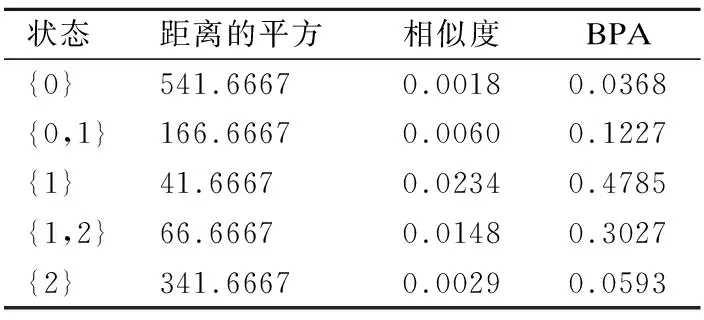
表5 第6个时间点上的数据的BPATable 5 BPA of data at sixth time points

对剩下的其余所有时间点上的数据重复上述过程，可以获得每个时间点上的数据的基本概率赋值，见表6.

表6 20个时间点上数据的BPA Table 6 BPA of data at 20 time points

4.3 获得状态转移概率矩阵

由表6可以看出每个数据的BPA都不为0.所以公式(5)可以推导为：

(8)

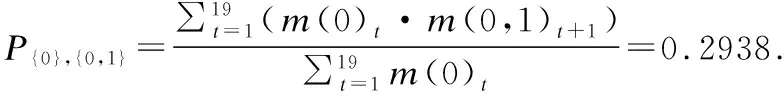
4.4 结果分析

通过上述获得的第20个时间点的BPA和状态转移概率矩阵，利用公式(6)可以计算第21个时间点的BPA：

m(21)=m(20)·P=(0.0922 0.1288 0.1487 0.3472 0.2831)

然后利用公式(7)将第21个时间点的BPA转化为基础状态的概率分布，即：

BetP({0})=0.0922+0.1288/2=0.1566

BetP({1})=0.1288/2+0.1487+0.3472/2=0.3867

BetP({2})=0.3472/2+0.2831=0.4567

最后得到P({0},{1},{2})=(0.1566,0.3867,0.4567).所以在第21个时间点上设备最可能处于失效状态.在实际中，相同设备在第21个时间上的确已经失效，这与预测结果相符合.

由于第3、6、13、16个时间点上的数据是不确定的，我们利用matlab软件随机生成4个数据，然后基于本文的方法得到状态转移概率矩阵：

利用公式(6)可以计算第21个时间点的BPA:

m(21)=m(20)·P=(0.0803 0.1221 0.1938 0.3571 0.2427)

然后利用公式(7)得到P({0},{1},{2})=(0.1414,0.4334,0.4213).最后结果表明设备更可能处于健康状态1，这与实际情况不符合，所以利用区间数来处理不确定数据能更精确的预测设备的健康状态.

另外，为了验证本文所提方法的改进性，我们利用文献[15]中的方法来进行比较.首先采用拉依达准则法剔除样本数据中不确定的数据.拉依达准则如下：有在线监测数据序列X={x(1),x(2),…,x(n)}，若采样点x(i)满足公式(9)，则认为x(i)为不确定数据应剔除.

|x(i)-x|>3σ

(9)

5 结 论

本文提出了一种针对数据不确定下如何处理设备健康预测的新方法.提出的DS-MM框架能够有效对设备的健康状态进行预测.考虑到区间数的性质，利用区间数来表示不确定的数据，并基于区间数之间的距离和相似度来作为产生BPA的证据，为了使预测结果更加可靠，利用Pignistic概率转换将BPA转化为基础状态的概率分布.最后，通过设备健康预测的案例分析验证了该方法的有效性.

本文的新方法能够有效解决机械设备健康预测中存在的数据不确定情况.但是本文仅给出了基于DS-MM模型的设备健康预测，而设备健康预测的目的是进行设备维修决策，因此下一步是根据预测结果进行设备预测维修决策的研究.