一种面向OpenCL架构的矩阵-向量乘并行算法与实现

肖 汉,周清雷,姚鹏姿

1(郑州师范学院 信息科学与技术学院,郑州 450044)2(郑州大学 信息工程学院,郑州 450001)

1 引 言

科学技术的发展日新月异,当今许多应用领域如电路仿真模拟、数学建模和网络分析等都需用到矩阵-向量乘法算法[1].随着现代工程问题复杂度的提升,计算过程运算尺度大、运算数据量剧增,造成矩阵-向量乘法运算过程的效率低,导致无法满足应用系统实时处理的要求,限制了其发展.因此,人们对矩阵-向量乘法的运算速度的要求越来越高[2,3].

运用昂贵的服务器、工作站等设备,多核计算平台和计算机集群系统能够在一定程度上提供了较强的并行处理能力,但是在数据量较大时容易出现传输瓶颈,制约了性能的进一步提高.同时,将算法部署在工作站和计算机集群系统上,将造成硬件成本上升,软件研发过程复杂;而采用多核处理器进行性能提升,则存在器件集成度较低、功耗较高、价格昂贵等不足[4,5].而通过图形处理器(Graphic Processing Unit,GPU)的并行计算,将使计算机的运算效率得到很大的提升,GPU以其高速的浮点运算能力用于通用计算越来越引起人们的重视,GPU加速的矩阵-向量乘并行算法的优化与实现将是一个研究的热点[6].

开放式计算语言(Open Computing Language,OpenCL)不仅仅是一种编程语言,更是一个能帮助开发者充分而合理的利用整个计算机系统的所有计算资源,并挖掘和发挥出其中计算能力的跨平台异构框架,即完整的在异构平台上并行编程的开放框架标准,它包括编程语言、API、函数库以及运行时系统来支持软件在整个平台上的开发.

2 相关研究工作

近年来,关于矩阵-向量乘法算法的并行化处理和优化已有许多工作,代表性的工作主要有:Zhang Jilin等[7]提出了采用缓存遗忘的扩展四叉树存储结构的稀疏矩阵-向量乘法,与CSR格式相比,达到了1.5倍加速.邬贵明等[8]提出了稀疏矩阵二维均匀分块方法和相应的表示方法嵌套分块CSR,将有效开发定制结构的并行性.Gao Zhen等[9]提出了一种基于FPGA的整数并行矩阵-向量乘法的容错设计方法,显著降低了算法开销和容错成本.苏锦柱等[10]提出了一种基于FPGA的二元域大型稀疏矩阵向量乘SpMV的环网硬件系统架构,相对于PR模型获得了2.65倍的加速比.薛永江等[11]提出了一种基于FPGA的浮点数格式,二叉树数据流的矩阵向量乘法器,与软件执行相比,双精度运算速度能达到其3倍.Malovichko M等[12]使用OpenMP加速矩阵向量乘法,提出了一种用积分方程方法进行频域声学建模的并行算法.Hassan Somaia A等[13]通过使用AVX指令集、内存访问优化和OpenMP并行化,提出了一种单精度矩阵-向量乘法的优化算法,性能提升了18.2%.吴长茂等[14]通过在CPU和MIC以及网络间实现了异步计算和异步数据传输,设计了SpMV并行算法,使得行星流体动力学数值模拟在CPU-MIC异构众核环境下获得了6.93倍的加速比.张爱民等[15]针对Intel Xeon Phi的体系结构特点,提出了一种通用的分块压缩存储表示的SpMV并行算法,性能比MKL的CSR算法平均快2.05倍.李政等[16]根据油藏模拟线性解法器的算法要求,设计了基于一种块混合结构稀疏存储格式及其对应的GPU线程组并行策略的SpMV并行算法,相对串行BCSR格式的SpMV的加速比可达19倍.Liang Yun等[17]提出了基于OpenCL硬件遗忘实现和基于至强Phi本地编程语言的硬件有意识实现的稀疏矩阵向量乘法,并分别获得了2.2倍和3.1倍加速比.

这些研究表明,并行计算的应用能够极大地减少处理时间,系统性能得到了有效提高.但是这种高计算效率多获益于一些比较传统的并行处理技术的运用,却没有与目前主流的并行计算技术所产生的效率优劣势的对比,以至于并行化方案并没有充分发挥出系统的效率.此外,部分研究虽然采用了当今比较流行的硬件架构和计算模型,但是多针对单一的并行计算技术进行算法的改进,多算法跨平台系统的性能评估较少.本文将根据矩阵-向量乘算法的特点和OpenCL架构特征,实现了基于GPU加速的矩阵-向量乘并行算法和算法在不同计算平台上的性能移植.

3 OpenCL并行计算引擎

OpenCL并行计算引擎的执行模型分为两个部分,一部分是通过主机端CPU系统执行,另一部分是通过设备端在若干个OpenCL设备上执行的内核.OpenCL通过使用主机端系统对多个支持OpenCL的计算设备进行定义上下文并管理内核的调度,通过主机端内存和设备端存储器,共同完成整个系统的运行[18].

出于对系统的可移植性的考虑,OpenCL定义了一个抽象的存储器模型,它能够将该存储器模型映射到实际的设备存储器系统中.OpenCL将内核程序中用到的存储器分为了四类不同的类型:本地存储器(Local Memory)、常量存储器(Constant Memory)、全局存储器(Global Memory)和私有存储器(Private Memory),如图1所示[19,20].

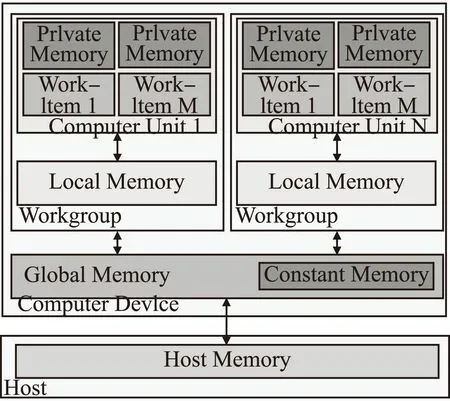
图1 OpenCL存储器模型Fig.1 OpenCL memory model

① 私有存储器:只从属于当前的工作节点,私有存储器中的数据通常映射到寄存器.一个工作项内部的私有缓冲区对于其他工作项是完全不可见的.

② 本地存储器:从属于一个工作组的存储器,同一个工作组中所有的工作项都可以共享使用本地存储器.可用来分配一些由该工作组中所有工作项共享的数据,它通常位于片上,与全局存储器相比较,带宽更高,访问延迟更短,但容量非常有限.

③ 常量存储器:带有缓存的全局存储器,是全局存储器的一部分,工作空间内所有的工作项可以只读常量存储器中的任意元素,而不是特意针对某种只读数据类型.

④ 全局存储器:工作空间内所有的工作项都可以读/写全局存储器中的任意位置元素.

4 在OpenCL中的并行化实现和优化

4.1 并行算法描述

矩阵-向量乘法将一个n×n阶的方阵A=[aij]乘以n×1的列向量B=[b1,b2,…,bn]T可得一个n×1的列向量C=[c1,c2,…,cn]T:

根据OpenCL架构的特点,在行带状划分矩阵-向量乘法中,设每个工作组内工作项数量为S,对方阵A按行划分为p块,每块含有连续的S行行向量,p=「n/S⎤,这些行块依次记为A0,A1,…,Ap-1,分别存放在索引号为0,1,…,p-1的工作组中,同时所有工作组将接收来自系统广播的列向量B.存储于局部数组a中的行块Ai和列向量B在各工作组中并行做乘积运算,矩阵-向量乘并行算法具体描述如下:

算法.行带状划分的矩阵向量乘法并行算法

输入:矩阵An×n,向量Bn×1.

输出:向量Cn×1.

Begin

forall work-grouppar-do

fori=0top-1do

c[i]=0.0

forj=0ton-1do

c[i]=c[i]+a[i,j]*b[j]

endfor

endfor

endfor

End

4.2 并行算法执行模式

基于OpenCL的矩阵-向量乘GPU并行化处理执行模式如图2所示.

矩阵向量乘并行算法实现的主要工作过程如下:

1)进行平台创建和初始化OpenCL设备.

2)创建上下文.通过在主机端创建这种抽象容器,实现在主机与设备之间进行相应的协调、交互,并对设备上的可用存储器进行管理、安排.

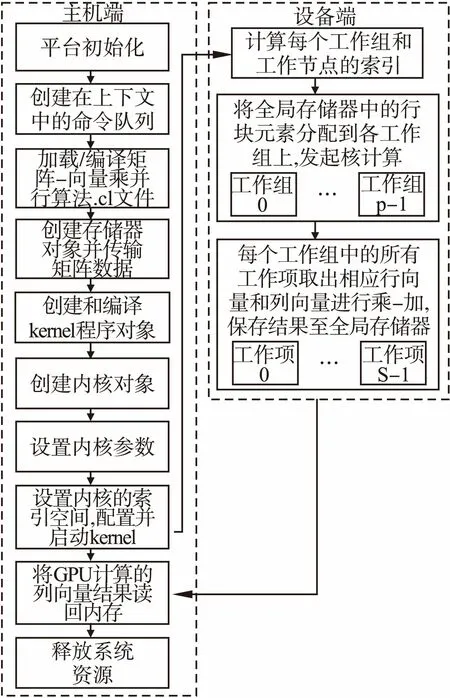
图2 矩阵-向量乘并行算法执行模式Fig.2 Matrix-vector multiplication parallel algorithm execution mode

3)创建命令队列.将提交的命令与设备进行通信,命令队列是主机端向相应的设备端传递消息和发送请求的一种行为机制.

4)创建设备缓存.创建三个buffer用来读入矩阵A、列向量B和输出列向量C.

5)将主机端数据写入设备存储器.将矩阵A和列向量B分别写入全局存储器和常量存储器中,用来完成数据的传递.

6)编译程序对象.通过clCreateProgramWithSource()将kernel转化为一个cl_program对象,再使用clBuildProgram()编译kernel.

7)创建kernel对象.将主机端传来的矩阵A和列向量B对象进行乘积操作.

8)将输出读回主机端并释放OpenCL资源.将输出结果列向量C读到主机端内存.

4.3 矩阵-向量乘并行算法设计

1)两级并行计算

根据矩阵-向量乘并行算法执行模式,需要将矩阵A进行分块,将大规模的矩阵划分为小规模的行块Ai进行处理.每个工作组按照获得的坐标get_group_id(0)位置将相应的行块Ai调度到计算单元中.每个工作组中的每个工作项按照获得的坐标get_local_id(0)位置将相应的矩阵行和常量存储器中的列向量B做乘―加运算.在矩阵-向量乘并行算法中,工作组负责行块Ai的数据处理,每个工作项负责将相应坐标位置上的行向量和列向量B调度到相应处理单元中做乘―加运算,从常量存储器中取出列向量B并将列向量C存储到全局存储器中.同一个工作组中的工作项可以通过work_group_barrier()进行同步处理.

矩阵-向量乘法算法的并行计算按照在工作组进行粗粒度并行计算和在工作项进行细粒度并行计算的两个层次进行组织.粗粒度并行是存在于同一N维工作空间NDRange内的不同工作组之间,不同工作组之间不需要进行数据的通信和交换,使得并行算法系统可扩展性很好:由于一个计算单元上可以任意运行每个工作组中的子任务,因此,基于OpenCL的矩阵-向量乘并行计算系统在核心数量不同的GPU上都能正常运行.细粒度并行是存在于同一工作组内的工作项之间,同一工作组内的工作项之间需要进行数据的交换和通信.

2)内核函数配置

根据互不重叠的矩阵行块数量,整个矩阵可以划分成若干个行块,每个行块在GPU中可作为一个基本处理单位,分割出来的大量行块的计算可由工作空间和工作组处理.从数据层面上看,GeForce GTX 980中拥有16个计算处理单元,一个计算处理单元可同时处理32个行块.所以,在GPU中可并行处理512个行块.矩阵-向量乘并行算法将n作为工作空间在x方向上的长度,行块的大小S作为每个工作组内工作项值,核函数的网格配置如下:

size_tlocalWorkSize[]=(S)

size_tglobalWorkSize[]=(n)

clEnqueueNDRangeKernel

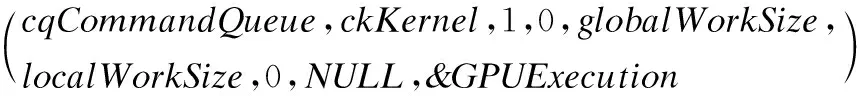
3)工作项映射模型

为了标记行块中每个工作项在工作空间中的位置,利用OpenCL内建函数建立了工作项的ID索引workItemID,如下所示:

workItemID=get_local_id(0)+get_group_id(0)*get_local_size(0)

4.4 优化策略

OpenCL存储模型包含了可以访问的多种快速存储区域,如私有存储器、本地存储器和常量存储器等,合理地对快速存储器的运用,将会使算法获得更高的性能.由于在矩阵-向量乘并行算法的处理过程中,列向量B是不会改变的,而且每个工作项的处理都要用到该列向量.为了提高运行效率,本算法选择把列向量B的内容传递到常量存储器,并且常量存储器带有缓存机制,这样能进一步提高每个工作项访问列向量B的效率,加速了算法的运算速度.

5 实验测试及设计

5.1 测试平台和实验数据

1)硬件环境

研究平台:图形处理器采用GeForce GTX 980,拥有2048颗计算核心,其流处理器频率为1216MHz,核心频率为1126MHz,GPU显存位宽为256位,GPU显存带宽为224GB/s,显存为4GB GDDR5.

对比平台1:GPU为AMD Radeon HD5850,共有1440个流处理单元,核心频率为725MHz;GDDR5显存,频率为1050MHz,容量为1GB,位宽为256bits.

对比平台2:CPU为Intel i5 8400 2.8GHz(六核心),系统存储器为8.0GB.

2)软件环境

操作系统采用Windows7 64bits;集成研发工具为Visual Studio 2013;环境支持为CUDA Toolkit 7.5,内部支持OpenCL 1.2.

实验采用矩阵大小分别为5×5、10×10、50×50、100×100、500×500、1000×1000、2000×2000共7组实验数据,并将矩阵乘法算法分别运行于基于CPU的OpenMP系统、基于NVIDIA GPU的CUDA系统、基于AMD GPU的OpenCL系统和基于NVIDIA GPU的OpenCL系统,并记录处理时间,如表1所示.

为了验证各种架构下并行算法的效率,可以直观地用加速比作为加速效果的衡量标准,其定义如下:

表1 不同计算平台下矩阵-向量乘算法执行时间(s)

Table 1 Matrix-vector multiplication algorithm execution time under different computing platforms

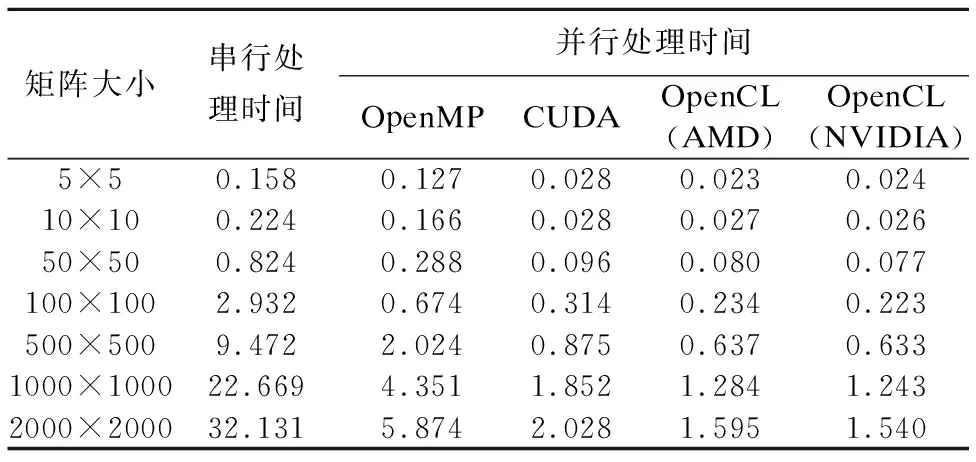
矩阵大小串行处理时间并行处理时间OpenMPCUDAOpenCL(AMD)OpenCL(NVIDIA)5×50.1580.1270.0280.0230.02410×100.2240.1660.0280.0270.02650×500.8240.2880.0960.0800.077100×1002.9320.6740.3140.2340.223500×5009.4722.0240.8750.6370.6331000×100022.6694.3511.8521.2841.2432000×200032.1315.8742.0281.5951.540

加速比是指CPU串行算法执行时间与并行算法执行时间的比值.

表2 不同计算平台下矩阵-向量乘并行算法性能对比
Table 2 Performance comparison of parallel algorithm of matrix-vector multiplication on different computing platforms

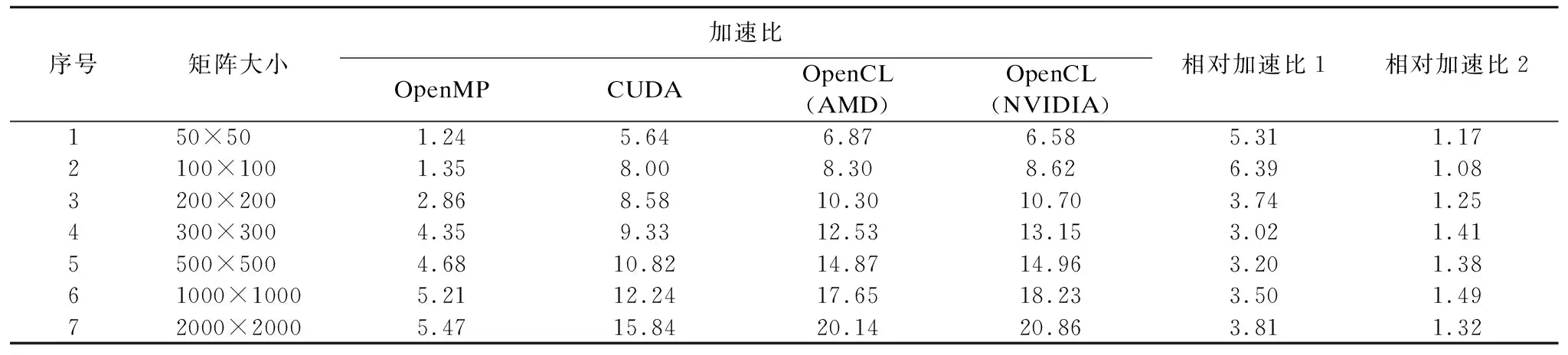
序号矩阵大小加速比 OpenMPCUDA OpenCL(AMD)OpenCL(NVIDIA)相对加速比1相对加速比2150×501.245.646.876.585.311.172100×1001.358.008.308.626.391.083200×2002.868.5810.3010.703.741.254300×3004.359.3312.5313.153.021.415500×5004.6810.8214.8714.963.201.3861000×10005.2112.2417.6518.233.501.4972000×20005.4715.8420.1420.863.811.32

相对加速比1是指基于CPU的OpenMP并行算法执行时间与基于NVIDIA GPU的OpenCL并行算法执行时间的比值.

相对加速比2是指基于NVIDIA GPU的CUDA并行算法执行时间与基于NVIDIA GPU的OpenCL并行算法运行时间的之比.

相应计算架构下GPU并行算法相比CPU串行算法整体性能提升情况可用加速比反映,可用于对系统性能改进程度的衡量,如表2所示.而相对加速比1则反映出基于OpenCL的NVIDIA GPU并行算法相比基于OpenMP的多核CPU并行算法的性能提升程度,相对加速比2则反映出基于OpenCL的NVIDIA GPU并行算法相比基于CUDA的GPU并行算法的性能提升程度.

5.2 并行算法性能分析

1)矩阵-向量乘并行算法加速比性能分析

图3显示了在不同计算平台下矩阵-向量乘并行算法的加速比对比曲线.从中看出,随着矩阵大小的增加,基于OpenMP算法的加速比不断地增加,但是由于CPU核心数有限,加速比较小且增幅较小.而经过CUDA和OpenCL加速的矩阵-向量乘并行算法,由于GPU计算资源充裕并且可以创建充足的工作项来满足大量数据的并行处理,通过时间分割的机制将工作项分配到2048个处理单元中,获得的加速比较大且增幅较大.从中反映出基于GPU运算对于计算密集型的运算不如CPU敏感,在面对大规模数据的计算密集型运算时,GPU计算时间的增幅很小,体现出GPU强大的计算能力.

由图3可知,随着矩阵规模的增加,GPU的加速效果十分明显,例如:对于2000×2000大小的矩阵-向量乘法运算,获得了近21倍加速比.然而,GPU并行处理系统性能的提高并非线性增长,而是随着矩阵规模的增加,呈现出缓慢提升的趋势.这是由于当矩阵规模增大时,PCI-E总线带宽有限,GPU显存与主机内存间数据传输通信耗时较多,通信瓶颈现象明显出现.内存与显存之间的传输时间极大地抵消了GPU并行计算优势,GPU加速比增幅缓慢,制约了系统整体性能的提升.

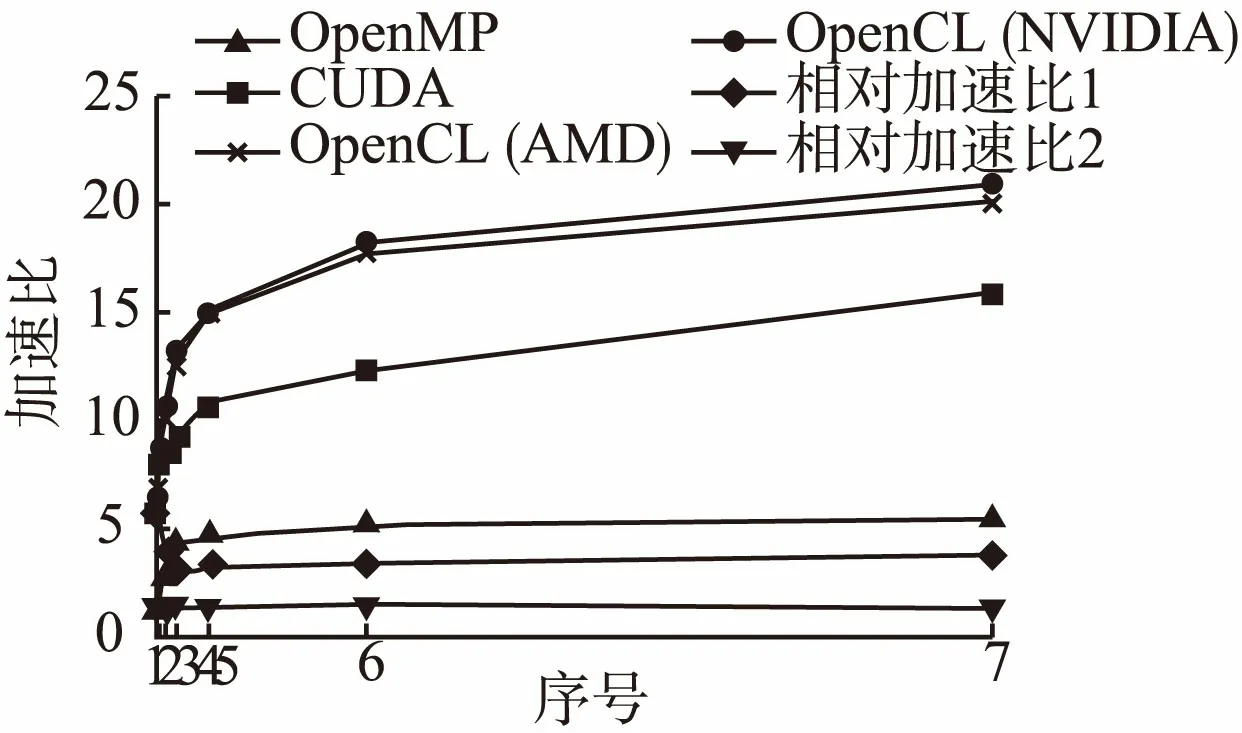
图3 矩阵-向量乘并行算法的加速比对比Fig.3 Comparison of acceleration ratios of matrix-vector multiplication parallel algorithm

2)基于OpenCL的矩阵-向量乘并行算法跨平台性分析

图3表明,算法源码级别的可移植性不仅要求源码可以在不同的平台上成功的编译和运行,而且还要求算法保持相当的性能.实验表明,基于CUDA的矩阵-向量乘并行算法受到硬件平台的限制,而基于OpenCL的矩阵-向量乘并行算法在多种硬件平台上具备最大程度的可移植性和兼容性,其算法性能与OpenMP计算平台和CUDA计算平台上的算法性能基本相近并略有提升.

6 结束语

本文对OpenCL计算平台的并行架构和矩阵-向量乘法算法的并行层次进行了详细的讨论和分析,提出了矩阵-向量乘法算法的GPU并行化实现方法,并对其并行算法和关键技术:两级并行计算,工作项映射模型与性能优化等问题进行了详细论述.实验结果表明,与基于CPU的串行算法、基于CPU的OpenMP并行算法和基于GPU的CUDA并行算法的性能相比,优化后的基于OpenCL的矩阵-向量乘并行算法分别获得了20.86倍、6.39倍和1.49倍的加速比,不仅实现了高性能,而且实现了在不同计算平台间的性能移植.本文采用的优化方法,充分利用了GPU强大的众核并行处理能力和OpenCL架构良好的可移植性,数值计算能够被有效地加速,为进行跨平台高速大规模数据运算的提供了一条新的思路.今后将进一步研究如何将GPU和集群的计算能力进行整合,形成CPU+GPU多节点GPU集群,以满足更大规模的矩阵对计算能力的需求.