机器学习技术在气动优化中的应用

陈海昕，邓凯文，李润泽

清华大学 航天航空学院，北京 100084

气动优化设计作为飞行器设计的重要组成部分，复杂程度相当高，存在大量需要考虑且互相影响的因素。在超临界机翼优化中，除需考虑巡航升阻力系数、升阻比、力矩系数等设计点性能外，抖振、阻力发散、阻力蠕增等非设计点动态特性也需纳入考虑范围；同时优化还存在一些不可忽略的约束，如机翼厚度、油箱容积、前后缘装置；更多地，压力分布形态、失速起始位置和形态等流动形态的期望也应纳入考虑范围。以上性能要求与几何外形之间的关联十分敏感和复杂，呈现强烈的非线性。气动优化可以协调复杂的设计变量、目标和约束，提升飞行器综合性能，近年来在飞行器设计中得到越来越广泛、深入的使用。在C919飞机的气动设计中，优化设计展现了巨大的优势和能力，获得了良好的效果[1-2]。

在气动优化方法出现之前，气动设计主要依靠风洞试验和简化的理论计算，依赖设计人员的经验以试凑法(Cut and Try)进行。在复杂问题面前，人的试凑设计常表现出顾此失彼、重复浪费、搜索受认识局限等缺陷。优化方法则在这些问题上相应地展现出其优势。

gi(x)≤0i=1,2,…,Ng

hi(x)=0i=1,2,…,Nh

对气动优化而言，设计变量x通常为待进行优化的几何外形控制点坐标、工况等，优化目标y通常为气动性能(如升阻特性等)。为消除歧义，本文所指的优化方法是由计算机为主实现的、以寻优算法配合数值模拟为主的评估手段进行的自动搜索寻优。图1给出了一个典型的气动优化设计流程。

基于数值模拟的气动优化有着超过40年的发展，从其发展历程来看，研究人员主要试图解决2类问题：① 在给定优化问题的情况下，研究寻优算法等，以更省时省力、又快又好地得到最优解，解决效率问题。除寻优算法本身的改进外，典型的例子是引入代理模型和降阶模型技术。② 如何合理地定义优化问题，运用寻优算法，使得到的解更符合实际的工程需求，即解决实用性问题。多学科优化和鲁棒性优化思想均属此方面的努力，前者将气动和结构、隐身等学科进行综合权衡，获取飞机最优综合性能。后者通过对不确定性进行建模以抑制工况变化带来的性能损失。

图2给出了气动优化发展的粗略时间线。图中：上方基本体现了人们改善寻优效率的历程，下方则体现了人们在解决实用性方面的努力。

图1 气动优化运行流程Fig.1 General flowchart of aerodynamic optimization

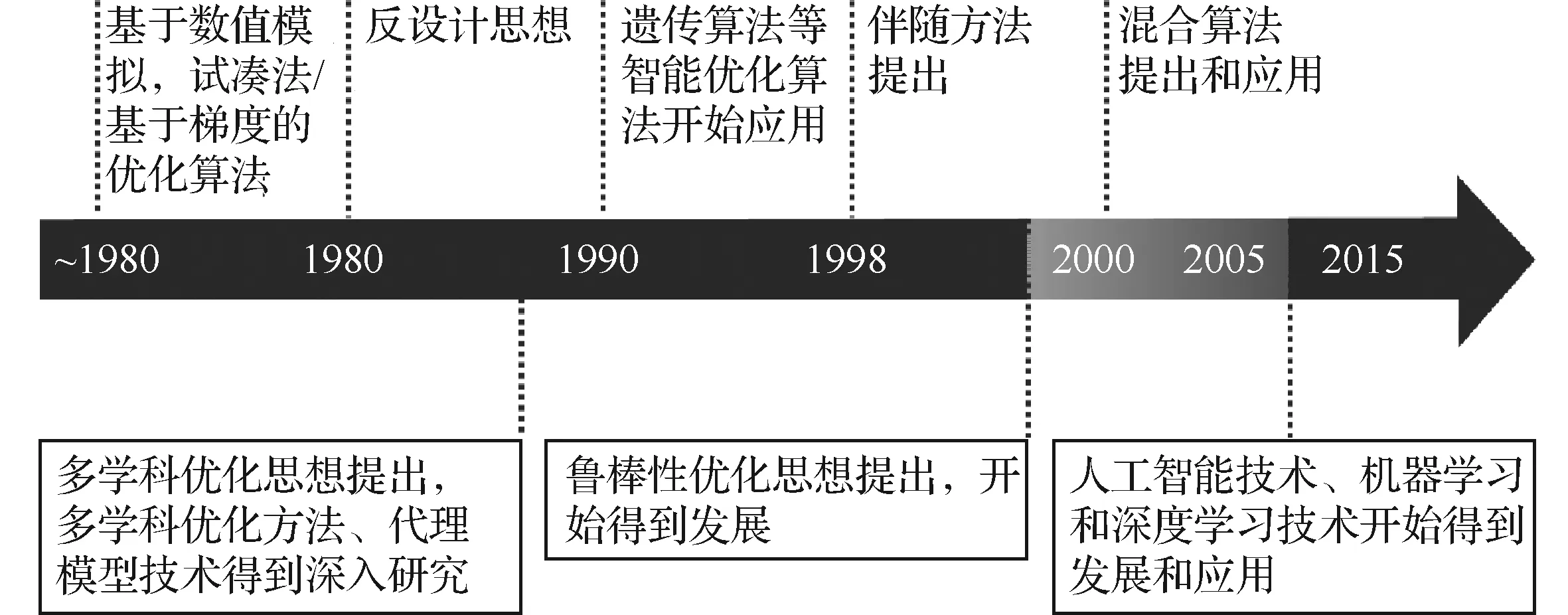
图2 气动优化发展的时间线Fig.2 Development timeline of aerodynamic optimization

1 气动优化设计

1.1 寻优算法的发展历程

气动优化的应用最早可见于20世纪70年代[3-7]，此时多使用小扰动方程、全势流等快速方法进行气动评估，并结合以共轭梯度法为代表的梯度类优化方法进行寻优。

在20世纪80～90年代，以遗传算法为代表的进化类算法，与蚁群算法、模拟退火算法等启发式的智能优化算法在气动优化中开始得到应用。此类方法由于不需引入梯度等额外信息，搜索方向具有不确定性，因而也被称为随机优化方法。随机优化方法可以构建自动通用的优化框架，使得使用者可将其视为黑箱而无需了解具体的运作细节，因而成为气动优化中很受欢迎的算法。在单次目标评估计算量不大时，如基于全势流方程或欧拉方程进行评估的二维优化问题或简单的反设计问题中[8-11]，取得了很好的效果，简单的三维优化问题也可以在该框架下成功解决[1-2,12-15]。

进化类算法以其较强的鲁棒性，对多变量多目标的天然适应性，使气动优化可以从单点、单目标、单学科优化自然地过渡到多点、多目标、多学科优化[16-19]。

进化类算法尽管具有种种优点，但其需要完成大量的适应度函数分析，优化效率较低。在复杂三维气动优化问题中的应用困难重重。20世纪90年代，伴随方法的提出[20]解决了气动优化中目标对设计变量梯度的求取问题。通过求解伴随场，伴随方法能以低廉的计算代价求得流场各点物理量对几何外形的敏感导数。因此在优化目标是以流场局部闭区间积分形式表示的情况下，可以直接应用伴随方法求得梯度，并使用局部优化效率强的、基于梯度的优化方法进行优化。这使得基于雷诺平均Navier-Stokes(RANS)、大涡模拟(LES)的三维复杂外形优化问题不再困难[21-25]。Zingg等[26]的研究表示，梯度类方法的优化效率可达进化类算法的5倍，但尽管如此，梯度类方法还是受限于易陷入局部最优且难以应对多个目标和约束等问题。

代理模型方法的发展和应用是另一个里程碑。代理模型又称为响应面或元模型方法，以类似拟合的方式从已知样本集构造简单模型替代复杂的计算流体力学(CFD)评估过程，从而显著降低优化过程中的计算需求，提高优化效率和质量。代理模型中常用的模型有二次多项式响应面、Kriging响应面、径向基函数(Radial Basis Function, RBF)响应面和多层感知机(Multi-Layer Perceptron, MLP)等。20世纪90年代，代理模型方法在气动优化中得到了大量应用[27-32]，一般直接利用寻优算法在所构造的代理模型上进行寻优。此类方法虽然建模时在训练样本集上可以达到很低的误差，但在未知的设计空间其误差则无法保证，导致寻优进程很容易被误导。

近年来，气动优化寻优算法的发展趋向于上述方法的改进和运用策略。如通过融合代理模型和降阶模型简化计算量，通过融合多种精度的代理模型和降阶模型进行分层搜索以提高优化的时间效率，通过对多目标加权降低优化复杂度，通过混合多种优化算法实现局部搜索和全局搜索能力的均衡，通过将优化分阶段提高搜索效率等。这些改进大多在具体问题上取得了收益，但本质都是对全局寻优能力和局部寻优能力进行折中。

1.2 优化设计的实用性改进

如图2所示，伴随着寻优算法的进步，气动优化在实用性上的发展起初主要是通过更为合理全面的设计准则，也就是设计变量、目标与约束的设定，来更真实合理地协调设计构型可能面对的工况和对性能的期望。文献[1-2]在C919飞机超临界机翼设计中进行了大量的尝试和努力，提出“多点优化”、“人在回路”、“压力分布形态约束”等策略，取得了很好的效果。

多学科优化通过将与气动耦合的其他特性纳入考虑范围，以优化算法进行权衡寻优，实现更综合可用的设计。鲁棒性优化关注降低设计点性能在工况变化时的性能损失风险。一般以设计点邻域内气动性能的方差进行表征[33-34]。对设计点邻域进行采样可使用蒙特卡罗为代表的方法进行。不难看出，多学科优化和鲁棒性优化都强烈依赖更多、更为复杂的目标和约束评估。以鲁棒优化为例，由于气动性能在设计点附近的敏感度要求大量额外的目标评估，很多情况下只能使用代理模型方法才使鲁棒性优化得以应用[35-43]。

为了应对多学科优化和鲁棒性优化中对多目标寻优的需要，人们发展了多目标优化算法。多目标优化研究起步于20世纪90年代，通常有2种处理方式：① 将多个目标的加权形成单个优化目标；② 基于Pareto占优准则进行真正的多目标优化。前者的问题在于权重的选择困难，且权重设置直接关系着优化结果。后者的问题在于其对目标数目有严格限制，Pareto占优准则在目标数目过多(≥3)时极易失效，这会使优化停滞。

约束同样是改善优化结果实用性的重要手段。如利用几何方面的相对厚度约束，确保翼型设计满足油箱容积和结构效率的要求。文献[1-2]在设置性能和几何约束外，还对压力分布形态建立了复杂的约束体系，以“迫使”优化产生期望的压力分布形态。然而过多、过细的约束将造成合乎约束的初始种群难以形成、演进困难等问题。

为了增强优化结果在实际环境下的可用性，单纯依靠更为面面俱到地设置目标、约束是存在困难的。在这种情况下想取得工程实用的解，气动优化仍很大程度依赖专家干预，这就是所谓“人在回路”思想[1-2,44]。狭义来讲，“人在回路”指的是由专家来监视优化进程，适时删除重复和性能较差的个体，根据自己的理解手动添加潜在优秀的个体，根据当前优化状况和走向改变相应的算法参数，重设和调整设计空间范围等，对优化进程起到引导的作用。

当然广义来说，专家还需在优化前和优化中设定和调整优化目标、设计变量、搜索空间、约束表达式和约束权重，并在优化结束后对已有解进行筛选和修改以满足更为复杂的要求。现有寻优算法可以很容易地附加数据分析功能，如定量地计算优化目标和变量间的相关性，给设计人员选择和制定优化参数提供指导，形成对专家的决策辅助，帮助更好地引导优化的方向，提升气动优化的效率和质量。

1.3 优化设计对信息的利用

目前，进化类优化算法可谓是一个黑箱数学游戏：给定x和y的对应关系，调节前者得到更优的后者，而对决定x和y之间的物理机理并不直接关心。代理模型方法同样可以对x到y的单层直接映射进行建模，代理模型对已有算例间体现的映射进行了存储和积累，然而它也不能推断该映射背后的物理机理。

在优化设计中，信息是分层级的，最表层的信息是设计变量和优化目标的映射关系，目前所有寻优算法都依赖这些信息进行寻优决策，在建立映射方面，寻优算法相对人而言优势极为明显。然而，专家相对于寻优算法显而易见的优势在于其知识层级、获取利用信息的渠道和方式要更为高明。因此，面对现有优化方法的能力不足，“人在回路”是一种无奈却有益的补充。

相对于映射关系，气动设计所涉及的潜在物理知识，即流动机理、其他学科知识、设计经验等是更为高层级的信息。与寻优算法相比，专家积累了大量此层级的知识，并能灵活地加以运用。如何使优化能够利用这一层级的知识和能力，是应该得到更多关注的问题。

2 传统机器学习与气动优化

机器学习在过去几十年得到了快速发展。一种较为广泛接受的定义为：“机器学习是一个构建和研究能从数据中进行学习的算法的学科”。这是维基百科中关于机器学习的定义。简单而言，机器学习是数据驱动的,用于对数据间的内部关系进行建模的方法。机器学习技术包含模型定义、模型评估和模型训练等多个部分。大部分机器学习技术都是“样例学习”，即需要提供一系列样本用于估计模型参数。在CFD中，机器学习已被应用于湍流模型[45-66]替代等。在气动优化设计中，机器学习的应用主要体现在代理模型(或响应面)构建、设计变量间关联的探索、降阶模型构建等方面。

2.1 构建代理模型辅助优化

机器学习方法在气动优化中最为典型的应用是从已计算的样本出发，基于高斯过程回归(典型如Kriging响应面)、多项式、RBF、神经网络等构建模型，从设计变量快速预测目标函数，以部分或完全取代CFD分析。本文将常见的响应面、代理模型及机器学习中用于回归分析的神经网络模型统称为代理模型。使用代理模型完全取代CFD过程的优化方法通常被称为基于代理模型的优化(Surrogate Based Optimization, SBO)，此类方法要求已获得一定数量的个体输入输出数据，用其构建一个代理模型，再使用该代理模型替代耗时的数值评估过程进行优化。而使用代理模型部分取代CFD过程的优化方法一般称为代理模型辅助的优化(Surrogate Aided Optimization, SAO)，或者基于代理模型的预评估(Inexact Pre-Evaluation, IPE)。在这种优化方法中，代理模型仅作为局部搜索工具，可理解为对已计算个体进行分析后给出优化方向的建议，可以看做是专家归纳思考的简单抽象，通常被整合在一个更大的优化算法框架中。

在当前的气动优化中，SBO仍是主流[42, 67-79]。韩忠华[80]综述了Kriging代理模型在气动优化中的应用。Chen和Agarwal[67]在优化钝后缘翼型时使用MLP来替代部分CFD计算，在MLP预测结果和CFD计算结果偏差较大时仅使用CFD的结果。Lamarsh[68]使用MLP替代转子叶片的动力学评估过程，结合渐进分析方法优化了叶片在3种工作状态下的马力。Su等[69]使用MLP模型结合种群控制的遗传算法对导弹的气动外形进行了优化。朱莉和高正红[70]使用MLP代替了气动优化中的CFD评估过程，并结合遗传算法用于翼型优化问题。Mengistu和Ghaly[71]使用同样的策略优化了跨声速冲力式涡轮机叶栅及亚声速压气机转子。蒙文巩等[72]使用相似的策略根据翼型速度和扭转角的不确定性优化了升阻比，并提升了其稳健性。白俊强等[42]使用RBF网络替代CFD评估，使用标准遗传算法对一个超临界翼型进行了稳健性优化，使其气动特性得到明显提高。Haryanto等[73]同样利用MLP模型结合遗传算法，对翼型升阻比进行了优化。周晨等[74]使用RBF网络结合多岛遗传算法进行翼型优化，显著提高了优化效率。王宏亮和席光[75]使用反向传播(BP)神经网络分别结合多目标遗传算法和粒子群算法对一个翼型进行优化，并采用多属性决策方法对最优解进行挑选。Zhang等[76]使用结合分层公平竞争和动态小生境技术的遗传算法(GA-HFCDN)优化了一个平面叶栅，提高了约8%的升阻比，目标评估采用基于CFD结果构建的MLP。黄江涛等[77]使用MLP和粒子群算法针对翼梢小翼后掠角和倾斜角的不确定性对其升阻比进行了鲁棒性优化，使最终升阻比提高了2%，飞行器整体阻力减少5 counts(count为阻力单位，无量纲量，1 count=0.000 1)。张彬乾等[78]利用RBF神经网络代替复杂目标函数的评估，结合松散式代理模型管理框架和遗传算法实现了对翼型的气动/隐身综合优化。Ju等[81]对比了MLP、RBF网络和SVM模型的拟合精度(皆使用遗传算法优化参数)，认定SVM的精度较高，并以此基于SVM、遗传算法和蒙特卡罗方法针对翼型表面粗糙度的不确定性对翼型升阻系数进行了鲁棒性优化。

SBO的应用虽然直观，但存在一些不可忽视的问题，如要求大量样本构建代理模型。可以看到，SBO优化的例子几乎都是样例易于获得的二维简单优化问题。另一个问题是，单纯依赖代理模型优化会使代理模型在局部的错误变化规律误导优化，以致产生错误的优化结果。图3给出了一个基于代理模型的优化结果，蓝色和黄色圆点为2种代理模型预测得到的Pareto前缘，三角形代表这些点经高精度CFD验证后得到的结果，可以看到其规律和分布完全不一致。

SAO将代理模型和进化算法进行混合，以鲁棒性和全局寻优能力强的进化算法作为优化主框架，使用CFD作为目标评估手段，代理模型仅归纳已计算个体，提供低精度预评估，为进化算法建议演化方向。

倪昂修等[82-83]提出了一种将NSGA-Ⅱ算法与Kriging响应面相混合的SAO算法，方晓明[84]将该算法应用于短舱的优化设计中。邓凯文和陈海昕[85-86]提出了一种基于差分进化(DE)和RBF响应面的算法。图4给出了将Kriging响应面和RBF响应面分别与DE算法混合得到的算法(DEKrig和DERBF)优化二维翼型时的收敛曲线对比。可以看到，相对于单纯的DE算法，SAO方法可以减少30%～50%的优化耗时，并保证最后的解是物理和可信的。

基于SAO的优化方法在大型客机设计中得到了深度应用。Giannakoglou等[87]使用MLP辅助遗传算法进行预评估，在多个翼型优化算例中证实该方法能显著减少CFD评估次数。Praveen和Duvigneau[88]在粒子群算法中使用RBF响应面进行预评估，在机翼优化的例子中证明，可以在保证优化质量的前提下显著降低CFD等昂贵评估工具的调用次数。Asouti等[89]提出了一种基于RBF响应面的异步SAO方法。Hacioglu[90]使用了一种组合MLP和遗传算法的混合方法，MLP作为局部搜索工具为遗传算法的种群填充精英个体，同时遗传算法的优化流程也引入了“分销策略”(Distribution Strategies, DS)，使得算法具有更好的全局寻优能力。Shahrokhi和Jahangirian[91]强调不能完全采用神经网络的估计值而使用基于正态分布采样的样本点构建MLP，若待评估点设计变量多数处于正态分布均值正负标准差内时使用MLP估计目标值，否则调用精确求解器(CFD)，将以上策略结合遗传算法优化了一个跨声速翼型，减少了约40%的CFD调用，获得了较好的效果。Ju和Zhang[35]使用经遗传算法和BP训练的MLP，结合蒙特卡罗方法和遗传算法对风力涡轮机翼型进行了鲁棒性优化，该MLP替代了蒙特卡罗采样频繁的CFD计算，极大地提高了优化效率。Pehlivanoglu和Yagiz[92]提出了一种多项式响应面、RBF网络和遗传算法结合的优化框架，使用多项式响应面构建全局代理模型，将设计变量空间网格化，将格点上的精英个体加入当代遗传算法种群，围绕以上个体构造局部RBF网络，在网络上寻优并将精英个体同样加入遗传算法种群，按照遗传算法的步骤进行迭代，并使用精确CFD求解器计算目标值，该方法被应用在翼型优化问题上。Iuliano和Pérez[93]提出了一种以SVM作为代理模型，使用遗传算法为局部优化工具的混合方法，其核心思想为通过初始样本集构造高精度的SVM，再使用遗传算法在SVM上寻找最优解，将寻得的最优解通过高精度模型(如CFD)进行评估，而后加入样本库更新SVM，循环往复以上步骤。

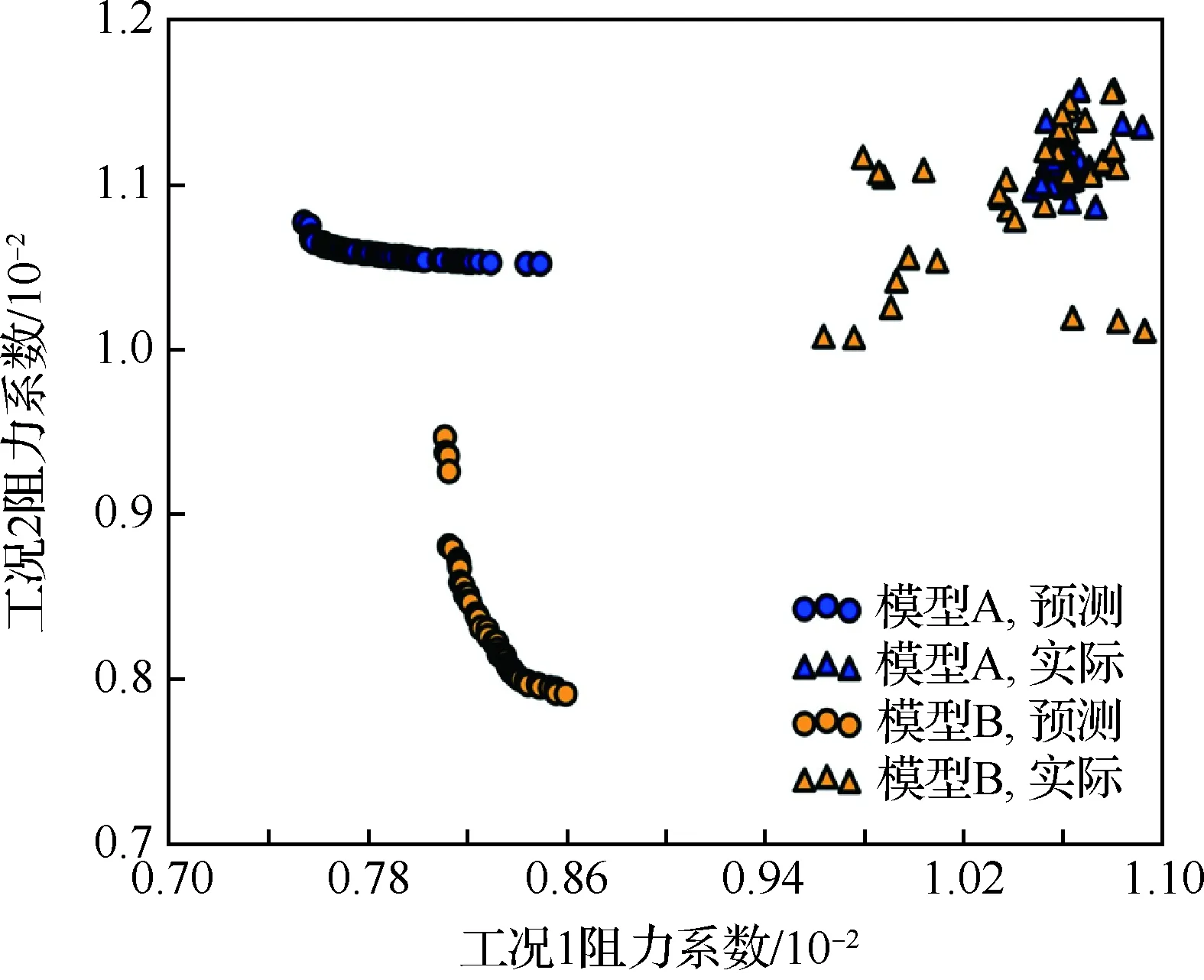
图3 基于代理模型的优化示例Fig.3 Example of surrogate based optimization

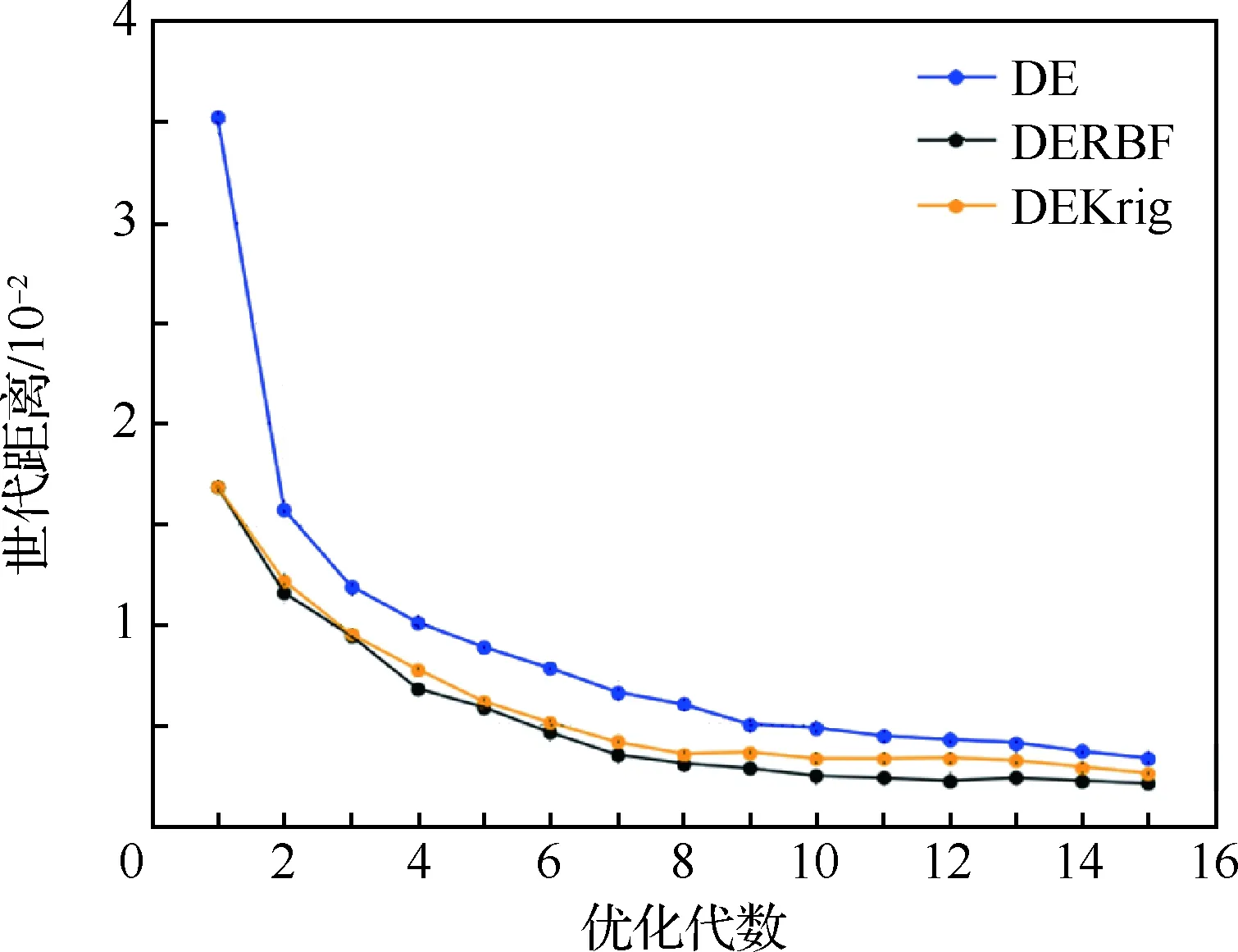
图4 代理模型辅助的优化示例Fig.4 Example of surrogate aided optimization

不同代理模型间也可以进行集成以提高精度和可用性。Rai[94]提出了一种结合MLP模型和多项式响应面模型的复合响应面的优化框架，并应用于压气机翼型设计，该框架根据目标对设计变量敏感度的区别将设计变量归纳为简单和复杂2种情况，前者用多项式响应面进行拟合，后者用MLP进行集合，采用单纯形方法进行搜索，使用两步策略拟合出给定点目标值。Papila等[95]采用上述优化框架，将MLP模型替换为RBF网络，用于压气机翼型设计，显著减少了优化计算量。Su等[96]将RBF网络进行Bagging和Boosting后形成2个新网络，并利用以上网络进行集成，结合网格自适应直接搜索方法进行翼型优化，结果表明，相较传统遗传算法，该方法可以显著减少计算量。

2.2 设计变量和优化目标相关性分析

机器学习方法用作代理模型时主要是用于回归预测，即关心的是模型在给定输入时输出的分布。有时研究者并不关心对应于某个具体输入其输出是多少，只想获得这些输入输出变量间的影响关系和相关性，以对精简设计变量和目标提供数据支持。以主成分分析(Principal Component Analysis,PCA)和自组织映射图(Self-Organizing Map, SOM)为代表的机器学习方法在此方面存在大量应用，可以很好地辅助设计人员确定设计变量和目标。

Chiba和Obayashi[97]使用SOM、方差分析(Analysis of Variance，ANOVA)和粗糙集理论(Rough Set Theory, RST)对进化算法优化可重用二级入轨飞行器的再入助推器机翼产生的数据库进行数据分析，分析表明，SOM可以进行各目标间的权衡分析，也可以给出对目标影响较大的设计变量和大致的影响规律，而ANOVA和RST都不能兼顾以上功能。Guo等[98]在优化跨声速轴流转子叶片时使用SOM对几个待选的优化目标进行了筛选精简，使用基于Kriging响应面的优化方法进行优化，并用ANOVA分析了目标对各设计变量的敏感度。Jung等[99]使用自适应遗传算法进行翼型优化，用SOM方法对设计变量进行了敏感度分析，发现翼型建模的24个PARSEC参数中起主导作用的有4个，即上表面前缘半径、上下表面最大厚度处的曲率和后缘位置。司景喆和孙刚[100]使用SOM分析叶尖翼型的几何特征和气动特性，利用置信度推理方法建立起几何参数和气动性能的关系，给出优化方向。Kapsoulis等[101]针对气动优化等昂贵问题可能存在的维数灾难，将PCA方法整合进遗传算法，在交叉和变异阶段使用PCA对设计变量进行降维，在降低优化复杂度的同时促使新个体的变化方向沿着方差最大的方向进行，以期提高优化效率。同时，PCA方法亦可用于降低针对高维问题的代理模型构建的复杂度。Toal等[102]提出了一种利用特征正交分解(Proper Orthogonal Decomposition，POD)方法降维筛选设计变量的方法，即在优秀个体几何中将待设计的气动外形/几何外形数据进行降维，选取基矢量对应的系数为新的设计变量以代表几何外形，以此为基础进行优化。

2.3 构建降阶模型

使用代理模型替代复杂的数值模拟过程的想法是比较直接的，但这种替代完全基于输入和输出的统计分析，而忽略了背后的流动机理。为在信息分析的层次上更进一步，另一种思路是使用机器学习方法对气动优化背后主导的偏微分方程组(Partial Differential Equations, PDE)进行降阶，以减少其复杂度，构建一个相对精简的降阶模型(Reduced Order Model, ROM)，继而进行快速求解预测。这种处理手段在代理模型中引入了物理信息，被一些学者称为基于物理的代理模型。机器学习方法在构建降阶模型方面应用广泛，其中最典型的手段即为PCA，或称为POD。目前依赖降阶模型进行气动优化的文献多结合了代理模型方法，即不对降阶后的PDE进行迭代求解，而训练一个代理模型来直接预测解，然后利用这些解重构出源方程的解(即流场)，通过积分等手段求出关心的气动性能。

Legresley和Alonso[103]利用已有的计算结果，使用POD方法对Euler方程中各格点物理量进行了线性降阶，在不改变方程和物理量数目的情况下极大地减小了计算复杂度，将Euler方程数值求解转化为求POD各基矢量系数使得新方程组残差最小化的过程，使用Levenberg-Marquardt方法进行快速求解并在翼型反设计的问题中进行了验证。Park等[104]延续了文献[103]的思路，在给定设计变量参数时，不再使用梯度算法迭代求解对应的POD基矢量的系数，而使用一个训练好的神经网络直接对其进行预测。Thomas等[105]将基于PCA/POD的降阶模型引入了三维机翼的气动弹性设计中，并发现在一组结构参数上构建的基矢量可以很好地应用于另一组结构参数上，并维持很高的精度。Agarwal和Biegler[106]发现使用PCA降阶的模型进行优化时，若脱离原PDE直接求得相关的系数，则这些系数很可能并不满足源方程组，导致求得的解在远离样本集合时可信度降低，据此提出了一种信赖域框架，用于引入以上脱离约束的考虑，限制优化过程中解的搜索空间从而使最终的优化结果更加可信且可用。Zahr和Farhat[107]应用了思路与文献[106]类似的方法，使用信赖域方法结合POD降阶模型和代理模型方法进行优化，并额外对源方程变量的导数进行降阶，以更好地应用于基于梯度的方法，在亚声速喷管外形优化中进行了应用，在保持0.1%错误率的同时能降低4～5倍的计算量。

PCA方法可以以很高的精度将高维流场变量降阶到低维，图5给出了将翼型上下表面压力分布(400维)降至10维再恢复后的效果，实线为源压力分布，圆点为恢复后的压力分布，可以看到两者基本是完全重合的,图中Cp为压力系数。

PCA方法实现简单，效果也常常能令人满意，但仍存在以下问题：

1) PCA是一种线性降维方法，虽然可以使用核函数转变为非线性，但由于可选用的核函数有限，因此PCA对非线性强变量多的PDE的降阶能力不强。

2) PCA在降维时将输入数据展成一维矢量，因此作为输入的流场，各格点物理量的空间联系和物理量间的联系都被抹去了。

3) PCA在降维过程中对各格点的物理量是单独处理的，不存在不变性，如平移不变性和缩放不变性等。

因此，使用PCA来模拟专家对流动的理解目前来看效果是难以满意的。更重要的是，专家具有从不同优化问题中提炼归纳共同点的能力，而PCA是问题相关的。

图5 PCA降维能力验证Fig.5 Validation of PCA based dimension reduction

3 深度学习与气动优化

近10年来，以深度学习为代表的人工智能/机器学习技术取得了令人瞩目的发展和成就，在图像分类领域，ImageNet 1000类图像分类挑战赛中的顶尖模型可达到约98%的准确率，超过人类平均水平的95%。在游戏博弈方面，AlphaGo及后继的AlphaGo Zero已经能轻松击败人类围棋冠军，棋力远超顶尖棋手。深度学习技术利用海量训练数据，展现出了极为强大的归纳学习能力。

深度学习相对于传统机器学习利用了更加复杂和深层次的模型结构，并在训练过程上进行了针对性的改进，使其归纳能力得到了极大的提升，应用范围也更加广阔。传统机器学习方法由于分析归纳能力有限，依赖使用者对特征进行精选以缩减问题规模，因此需要大量与问题相关先验的知识积淀，这样会带来优化设计的诸多困难。相反地，深度学习方法拥有强大的归纳学习能力，能够自主进行特征选择，可以从大量的候选特征中剔除无用特征，再进行回归和分类。

3.1 深度代理模型

深度学习较传统机器学习拥有更为强大的归纳能力，因此之前传统机器学习在气动优化中扮演的角色可以替换为深度学习来进行进一步的增强。

最直观的例子是可以利用深度神经网络构建深度的代理模型形成SBO或SAO。使用深度学习作为代理模型可以有以下好处：

1) 不需要对输入特征进行人工筛选和精简，可极大地减少对设计变量数目的限制，使得设计者能对几何外形的坐标点进行直接设计或使用更多的几何控制点。利用深度学习技术，设计变量可以细化为几何外形所有离散点的空间坐标，实现精细的外形优化。

2) 深度学习可以得到更加符合物理直觉的模型。如使用卷积神经网络对几何外形坐标点和气动性能的关系进行建模。输入数据是一个二阶或三阶张量，可以很好地保留坐标点间的空间相邻关系。同时，其特征提取过程具有空间上的平移不变性和缩放不变性。

3) 由于能够提取更深层次的特征，因而拥有更强大的归纳能力。使用深度代理模型不仅可以令关心的气动性能，还可以令一些流场特征作为代理模型的输出，如压力分布等。

3.2 深度降阶模型

可以利用深度神经网络构建更为复杂和精准的降阶模型。常用的基于PCA的降阶方法存在诸多问题：核函数单一，用于降阶的特征内部关联(空间关联、跨物理量关联)无法体现，最重要的是此类方法无法自定义降阶后的低维特征，因此丧失了可解释性。

而使用以卷积自动编码机(Convolutional AutoEncoder, CAE)为代表的深度学习模型可以实现质量更高的模型降阶和流场特征提取，此类方法有以下优点：

1) 输入输出的数据形式和流场数据格式一致，包含结构化的空间信息。输入输出张量的宽和高可以类比结构化网格流场数据的i方向和j方向网格数，通道数可类比各物理量分量。

2) 计算效率高，深度神经网络在使用GPU进行运算时计算效率非常高，比基于CPU运算的PCA降维要快。

3) 符合物理直觉，即特征提取过程具有空间上的平移和旋转不变性。

PCA方法可用的核函数有限，且只经过一次非线性变换，表达能力一般。而深度神经网络由于含有很深的层次结构，即使激活函数单一，在经过多个层次的非线性映射后理论上可以逼近任何未知映射。

图6展示了使用CAE对x轴方向无量纲速度u的速度场进行降维并利用反向变换进行重建的效果，并和PCA方法进行了对比。训练样本为12 000个二维翼型流场，包含6个通道的数据(x,y,u,v,p,T)，u和v分别为x、y方向归一化速度，p和T分别为归一化压强和温度，网格大小为256×96，降至维度为40维，信息压缩比率约为0.027%。CAE的编码器和解码器采用残差网络Resnet结构，总的网络参数量约为600万，网络约有近100层。

可以看出，经CAE提取的流场特征相对于PCA能够更好地保留信息和恢复流场。Wang等[108]应用长短期记忆循环(Long-Short Term Memory, LSTM)神经网络结合PCA对非定常流动控制方程进行降阶，具体处理手段为：对于0～Nt个时刻的流场精确解，使用PCA对其进行降维，得到基系数，以这些系数为LSTM输入，以下一时刻Nt+Δt的基系数作为输出进行建模。在使用该模型时，若已获得前0～Nt时刻的流场，即可对下一时刻的流场进行预测。Kani和Elsheikh[109]使用了与文献[108]一样的策略构建降阶模型，其循环神经网络使用了残差神经网络。不过以上研究仍使用的是传统PCA方法对流场进行降阶，使用到的深层循环神经网络仅是用于对时间序列间的关系进行建模。以上这些方法没有被应用在优化中，因此没有形成给优化算法提供更深层次信息的策略，仍被归类为对表层信息的挖掘和利用。

图6 PCA和CAE降维效果对比Fig.6 Comparison of dimension reduction performance between PCA and CAE

3.3 优化中对深层信息的利用

在气动优化中，所针对的问题处于流场被Navier-Stokes方程主控的物理背景中。传统机器学习和深度学习在优化中的行为主要是基于样本对空间流场数据进行了降维。更进一步，Farimani等[110]使用生成对抗网络(Generative Adversarial Network, GAN)构建了一个能按照任意边界条件生成满足控制方程的二维不可压方腔定常流动流场的模型，从而实现了对流场控制方程的降维。利用变分自动编码器，生成如对抗网络等的深度学习生成式模型，实现由流场数据对未知的控制方程进行建模，并根据输入条件(边界条件、几何外形等)生成满足控制方程流场。

综上所述，传统机器学习方法受限于信息处理能力，难以对优化中的高层次信息进行分析和归纳，并用于优化。而即便是深度学习发展的今天，尚没有一种行之有效的手段使其能“深度地”用于优化中,原因在于现有优化框架往往是基于设计变量和优化目标的。

本文认为专家在设计中对物理信息的利用方式并不全部来自对Navier-Stokes方程的求解，更不是只着眼于气动性能参数，更为直接的是针对流场结构(如旋涡、附面层、尾迹、激波等)进行观察分析，并通过修型实现对这些结构的调控，获得更全面均衡的性能。因此不妨彻底改变现有以性能指标为目标的优化框架，而增加流场结构为优化对象。

模仿气动专家进行优化时的行为和思路，可分为如下步骤：① 判断流场中存在哪些关键流动结构；② 分析这些结构如何影响所关心的性能；③ 分析几何外形如何影响这些流动结构；④ 如何合理地通过修改外形获得所关心的性能。

以上步骤可以使用机器学习或深度学习模型进行替代。文献[111]应用CAE(一种深度神经网络)提取流场的结构特征，利用MLP神经网络对流场结构特征、设计变量、优化目标的关联进行建模。利用MLP模型，可以求得目标函数对流场结构特征及流场结构特征对设计变量的梯度信息。依据这些梯度信息可对气动外形设计变量进行改进。根据上述模拟专家对流动结构进行分析利用的过程，在DE算法中，对个体进行改进，并引入种群实施种群引导，形成了一种改进混合优化算法。图7和图8对改进算法与传统DE算法进行了对比。展示的优化问题是二维翼型减阻，图7给出了优化目标为马赫数Ma=0.72下总阻力的单目标优化解的流场和压力分布对比，图8给出了优化目标为Ma=0.72和Ma=0.75下总阻力的双目标优化得到的Pareto前缘对比。

在图7表征的单目标优化流程中，改进混合算法得到的最优解相比于传统DE算法可进一步减阻0.7 counts，可以看出，引入模仿专家的个体改进方法的混合算法得到了典型的无激波、压力分布光滑且阻力更小的翼型，而传统DE算法得到的翼型表面存在轻微的曲率不连续，导致上翼面压力分布出现振荡，有二次加速和双激波。这可能是由于混合算法对大量流场特征与气动性能的关系进行了归纳，因而得出了抑制激波与光顺表面压力分布可以降低阻力的结论，因此可以在传统DE算法解的基础上进一步降低阻力并避免这种不合理的压力分布形态。而传统DE算法在搜索过程中陷入了局部最优，受限于寻优能力难以对已得到的性能较好但流动结构欠佳的解进行进一步的改进。

从图8同样可以看出，引入了流动特征分析的混合算法得到的Pareto前缘明显领先于传统DE算法。从以上结果可以基本看出，对深层流动相关信息的利用可以加快优化速度，并提高最终解的质量。

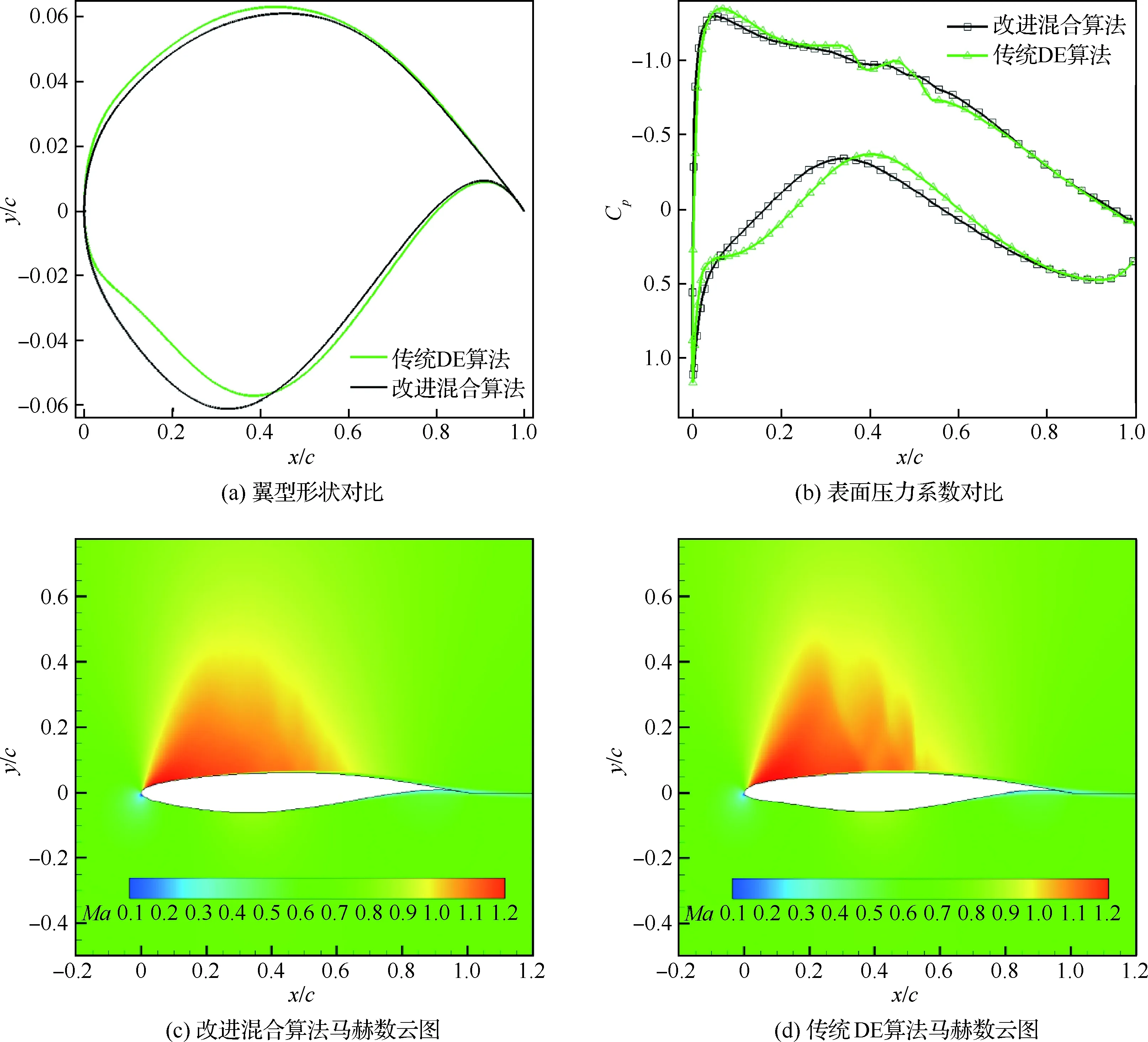
图7 单目标气动优化性能对比Fig.7 Comparison of performance in single objective aerodynamic optimization

图8 双目标气动优化Pareto前缘对比Fig.8 Comparison of Pareto front in double objective aerodynamic optimization

4 结 论

本文总结了机器学习在气动优化中应用的历史和现状。有效地给优化算法更多的信息用于决策是提高效率、改善效果的有效途径。机器学习技术，尤其是其中的深度学习技术非常适合对气动优化中的数据，尤其是缺乏关注的流场数据进行归纳和分析，从而对优化起到非常好的支持作用。本文也对深度学习在气动优化中可能的应用形式进行了探讨并进行了部分验证。

深度学习技术在气动优化中的应用尚处于起步阶段。由于深度学习训练依赖大量样本，因此存在所谓的"冷启动"(即在优化初期由于样本稀缺导致模型训练效果不佳，给顺利发展到样本充足阶段带来困难)的问题。如果没有在优化前积累一定数量的样本，对于从零开始且样本产生较为困难的优化过程，深度学习是不便于应用的，这也是其在气动优化中应用的最大困难。

已有的深度学习在空气动力学中的应用多是参考其在计算机视觉领域的成果,如陈海等[112]使用卷积神经网络根据翼型图像对其气动力系数进行了建模，显示获得了较高的精度。在优化方面,也可利用这一方法，利用流场后处理图像,使用基于深度学习的物体检测算法(检测出图像中给定类别的物体,进行标记和分类)对流场或流场图像中的流动结构(如激波、旋涡和分离区等)进行检测识别，进而重建流场,分析其与几何/性能间的关联，从而更好地支持优化设计。