大型客机涡扇发动机动力特性模拟

谭伟伟，颜洪，聂智军，马涂亮，梁益华,*

1. 西北工业大学 航空学院，西安 710072 2. 航空工业西安航空计算技术研究所，西安 710065 3. 中国商飞上海飞机设计研究院，上海 201210

在现代大型客机设计中，机体与发动机之间的相互干扰影响对评估和改善飞机气动性能至关重要[1-3]。20世纪80年代至今，国内外研究学者针对各种发动机进排气气动干扰问题，开展了理论、试验和数值计算等方面的研究。由于发动机内部进气、燃烧和喷气等过程十分复杂，导致试验研究存在难度高、周期长和费用高等问题，美国NASA(National Aeronautics and Space Administration)兰利研究中心用试验的方法[4]，采用涡轮动力模拟器对发动机短舱在机翼下不同安装位置的情况进行了大量研究，以达到减少动力效应带来的干扰阻力的目的。

随着计算机计算能力的逐年提升，计算流体力学(Computational Fluid Dynamics, CFD)技术也逐渐成为模拟发动机进排气气动干扰问题的最有效手段之一[5]，Hirose[6]和Deese[7]等通过求解Euler方程，模拟了发动机进排气效应，得到了进排气效应会引起发动机唇口激波强度变化的结论；上海飞机设计研究院张美红和王志栋[8]利用Ansys公司商用软件CFX，对带动力民用飞机进行了Navier-Stokes方程数值模拟，并应用到带动力气动设计中，谭兆光[9]和郝海兵[10]等建立模型，研究了机体/动力装置一体化分析中的动力效应。模拟方法上，不论是商业软件，还是研究机构的in-house代码，比如FUN3D、USM3D、NSU3D、TAU、FLUENT、CFX等，都是建立发动机动力特性模型来模拟，即在进气口设置质量流量比，排气口和外涵道设置总温比/总压比来等效模拟发动机动力特性。西北工业大学刘李涛等[11]提出了一种新的涡扇发动机动力特性计算模型，并基于特征变量法构造进排气边界条件，最终对外吹式动力吹气襟翼进行Navier-Stokes方程数值模拟，取得了较好的结果，但是该方法在整个边界面网格上指定均匀的质量流量，因此会影响计算的收敛性和精度。

本文作者在实际评估大型客机动力特性工作中，分析并实现了文献中的这些模型，并对这些模型进行了比较研究[12]，发现对大涵道比发动机，当前的这些模型计算所得发动机进排气口质量流量(绝对值)存在较大偏差，有时相对误差达到16%之多。因此，本文借鉴远场特征边界思想(保证流入、流出流场流体质量守恒)，将外涵道指定为特征边界，建立了一种新的发动机动力特性模型，并采用标模、某型客机等构型对该模型进行了系统的验证和确认。

1 研究方法

本文研究工作基础为自研非结构网格并行计算软件WoF90，是一款Euler/Navier-Stokes流动计算软件，基于格点格式有限体积法(所有离散均在对偶网格[13-16]上进行)，可处理多种单元类型(三角形、四边形、四面体、金字塔、三棱柱、六面体)的非结构/混合网格，支持中心格式、Roe、AUSM(Advection Upstream Splitting Method)系列以及LDFSS(Low Diffusion Flux Splitting Scheme)等多种空间离散格式，时间推进采用显式、点/线隐式Runge-Kutta方法，同时采用多重网格、当地时间步长和残值光顺等加速收敛技术。

1.1 基本求解器

在笛卡儿坐标系下，可压缩Navier-Stokes方程的表达式为

(1)

式中：U为流场守恒变量；FI与FV分别为无黏与黏性通量；Q为源项。将式(1)两端积分，则可得到可压缩Navier-Stokes方程的积分表达式为

(2)

其中:Ω为任意封闭参考区域；S为边界面；n为边界面单位外法向。

由式(2)可得有限体积法的数值离散方程为

(3)

式中：U0为网格顶点v0处的流场守恒变量；m0为与网格顶点v0相邻网格点的总数；S0k为连接网格顶点v0与相邻网格点vk(k=1,2,…,m0)的边所对应控制面的面积；n0k为该控制面的单位法向量；FI0k与FV0k为穿过该控制面的无黏通量和黏性通量；Q0和V0分别为网格顶点v0对应控制体上的源项和控制体体积。

1.2 涡扇发动机动力特性模型

由于发动机内部风扇进气、燃烧、喷气等过程十分复杂，工程上评估机体/发动机干扰问题时，通常需要采用简化模型，即在发动机进排气口设置等效的边界条件，建立发动机动力特性模型，来模拟发动机进排气效应，而不直接去模拟发动机内部的复杂流场。图1为典型民用涡扇发动机动力边界示意图。

在WoF90软件中，编程实现了文献[10]中的涡扇发动机动力特性模型A；同时分析、构造了一种新的涡扇发动机动力特性模型B。

如表1所示,分析、构造并实现的两种涡扇发动机动力特性模型主要涉及3种边界条件：发动机进气口边界条件(Nacelle_in)、发动机喷口边界条件(Nacelle_out)以及外涵道(特征)边界条件(Characteristic)。

图1 涡扇发动机动力边界示意图Fig.1 Sketch of boundary of turbofan engine with power

表1 两种涡扇发动机动力特性模型Table 1 Two models of turbofan engine with power

1.2.1 进气口边界条件

图2为亚声速发动机进气道的几何特性和进气道流动，图2(a)为高速飞行时捕捉到的流管；图2(b)为起飞和低速飞行时捕捉到的流管。进入压气机的流管有3个主要横截面面积(图2(a))：前方无穷远处的面积A∞(近似为发动机入口上游处流管剖面面积)，喉道面积A*和风扇入口面积Ainlet。

定义捕获面积ε为流过进气道捕获流管上游剖面质量流量与风扇入口质量流量之比：

(4)

发动机进气口边界采用静压条件，程序根据事先设定的目标流量(通过捕获面积ε来表达)，在计算过程中不断调节边界面静压，使实际流量尽快收敛到目标流量。

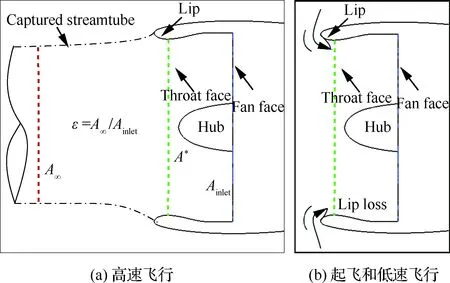
图2 亚声速发动机进气道特征和进气道流动[1]Fig.2 Characteristics of a subsonic engine intake and intake flow[1]

由等熵原理，风扇入口总压p0,inlet等于自由来流总压p0,∞。进而，风扇入口处静压为

(5)

式中：Mainlet为风扇入口马赫数；p0,∞的表达式为

(6)

因此，计算风扇入口马赫数Mainlet后，即可确定风扇入口静压。

由连续性方程ρAU=ρ*A*U*(A、U分别表示面积和速度大小，上标“*”表示声速喉道处的物理量)可知，发动机截面面积与声速喉道处的面积之比为

(7)

式中:T为温度;下标“0”表示滞止参数。

根据等熵关系式：

(8)

则有：

(9)

将式(9)代入式(7)，可以直接推导出面积比与马赫数之间的对应关系：

(10)

进一步引入拉瓦数，其定义为当地速度与临界声速之比，即La=U/c*,则自由来流拉瓦数和马赫数之间的关系为

(11)

式中：R为理想气体参数。

根据等熵关系式，可以确定自由来流拉瓦数和马赫数之间的关系为

(12)

将式(12)代入式(10)，最终推导出面积比与拉瓦数的关系为

(13)

为了获取风扇入口处拉瓦数Lainlet，重新定义了估算拉瓦数：

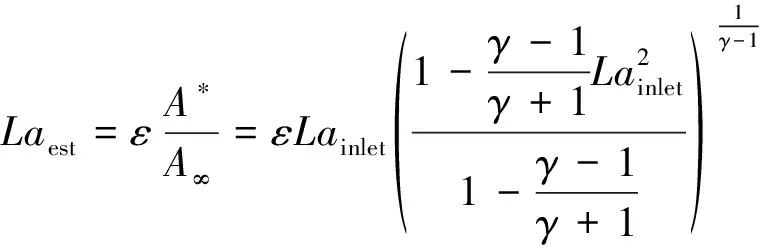
(14)

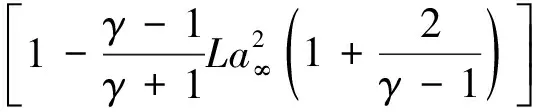
(15)

则由式(14)～式(15)可推导出下一步迭代的拉瓦数为

(16)

式中：松弛因子k可取k=0.875。通过对式(16)进行迭代求解收敛后(Δ≤1.0×10-10)，即可确定Lainlet，由拉瓦数-马赫数关系式(12)，可计算风扇入口处的马赫数：

(17)

进而可根据式(5)计算风扇入口处静压。

值得注意的是：① 进气口边界点上除了静压，其他流场变量(包括湍流变量)均通过流场内点外插得到；② 进气口边界条件实为流场出流条件，而下一节的喷口边界条件实为流场入流条件。

1.2.2 喷口边界条件

发动机喷口需给定出口处总温与自由来流总温之比TEx,ratio=T0,Ex/T0,∞和出口处总压与自由来流静压之比pEx,ratio=p0,Ex/p∞，给定喷口的总温比及总压比，即可求出总温和总压：

(18)

利用等熵关系式，可计算喷口处马赫数为

(19)

进而可计算得到喷口处的静温、静压和密度为

(20)

1.2.3 特征边界条件

文献[10]中的发动机动力特性模型(模型A)，其外涵道一般采用喷口边界条件。本文构造的模型B，借鉴特征边界思想，将外涵道指定为特征边界，得到一新的发动机动力特性模型，该模型基于质量守恒定律，保证了流入、流出流场的质量守恒，因此物理上可行。

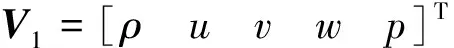
L=L(V∞,n)=

(21)

式中：V∞为自由来流原始变量；c为声速;n=[nxnynz]T。

L-1=L-1(V∞,n)=

(22)

然后根据特征值的符号确定特征变量W1的各分量：

(23)

式中:λi为第i个特征向量对应的特征值，具体表达式为

(24)

其中:u=[uvw]。

2 计算模型验证

为验证本文所构造和实现涡扇发动机动力特性模型的正确性和可靠性，分别对轴对称超高涵道比涡扇发动机模型(Counter Rotating Ultra-high-bypass Fan Simulator, CRUFS)，轴对称涡轮动力模型(Turbine Powered Simulator, TPS)的黏性流场进行了动力特性模拟，并与试验数据进行对比分析。在数值模拟中，主控方程对流项采用二阶中心格式，黏性项采用中心差分格式离散，时间推进采用线隐Runge-Kutta迭代法，并利用多重网格、当地时间步长及残值光顺等加速收敛方法，湍流模型均采用Spalart-Allmaras(S-A)一方程模型[17]。

若无特殊说明，本文所有算例中对称平面指定为对称边界条件，物面指定为绝热壁面边界条件，远场指定为特征边界条件。

2.1 CRUFS模型

CRUFS模型[18]为轴对称超高涵道比涡扇发动机模型。由于其超高涵道比，因此在计算中通常忽略内涵道，认为由进气道进入的气体全部由外涵道排出[19]。

2.1.1 计算网格及状态

CRUFS为对称模型，可采用半模计算。网格采用ICEM CFD网格生成器制作，附面层第1层网格高度给定为5×10-6m，拉伸比为1.2，网格总点数约为273万，远场长度约为50倍短舱外罩长度，支杆一直延伸到远场。发动机表面、进排气边界网格以及网格中心截面如图3所示。CRUFS模型仿真参数如表2所示,表中Re/L为单位长度雷诺数。

图3 CRUFS模型计算网格Fig.3 Computational grid of CRUFS model

表2 CRUFS模型仿真参数Table 2 Simulation parameters of CRUFS model

2.1.2 两种动力特性模型比较

验证涡扇发动机动力特性模型正确性的一个重要标准是：排除计算数值误差影响后，发动机进排气口质量流量是否一致。

首先考察收敛性，图4给出了风扇入口处质量流量收敛历史比较，两种动力特性模型虽然风扇入口边界条件一样，但不同的外涵边界条件导致模拟初期风扇入口质量流量有些许不同，迭代约1 800步后，两者逐步稳定并趋于一致，很快收敛到目标值2.001 kg/s。图中升力系数CL收敛历史特征类似风扇入口质量流量。

图4 CRUFS模型进气口流量收敛速度比较Fig.4 Comparison of convergence rates of mass flow through engine fan of CRUFS model

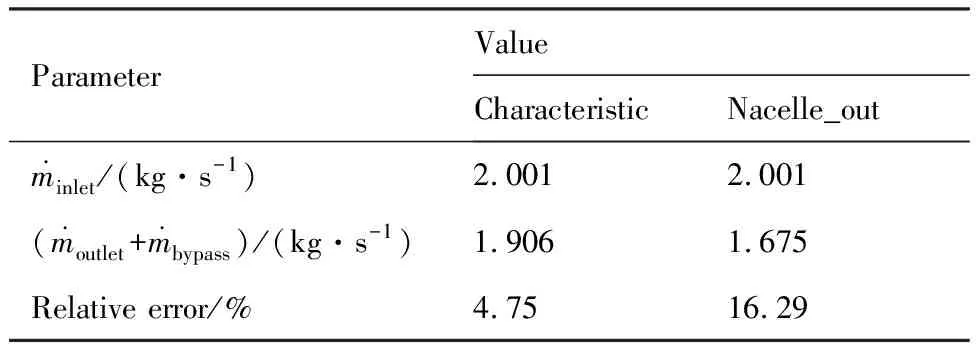
表3 外涵道边界类型对质量流量的影响(CRUFS)

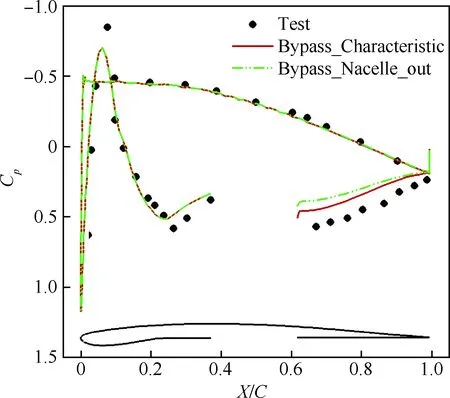
图5 CRUFS模型计算得到的压力系数分布比较Fig.5 Comparison of pressure coefficient distributions calculated by CRUFS model

2.1.3 流场分析

两种动力特性模型模拟所得流场比较接近，图6是动力特性模型B计算得到的流场马赫数等值线分布图。可以看到，由于风扇进气质量流量较大，进气道内喉道处加速区已经超过声速，最大马赫数约为1.2，风扇入口中心马赫数也达到了0.65。在短舱外表面有一加速区，但由于受风扇较大进气质量流量的影响，加速区最大马赫数未能超过声速。

此外，风扇出口处中心马赫数也在0.6附近，由于外涵道内气流量较大且为收缩型喷管，使得马赫数沿流向逐渐增大，且在外涵道出口附近达到最大值，约为0.85，随着流动向下游扩散，马赫数又逐渐降低到接近来流马赫数0.8附近。同时，在外涵道出口处，喷管排出的高速气流与外部气流混合，形成了较强的剪切流动。

图6 CRUFS模型计算得到的马赫数等值线Fig.6 Mach number contours calculated by CRUFS model

2.2 TPS模型

TPS模型[10,20]是一轴对称涡扇发动机模型，是日本航空宇宙技术研究所设计的风洞试验模型。模型包括风扇入口、内涵(喷口)及外涵3个部分。

2.2.1 计算网格及状态

TPS为对称模型，可采用半模计算。网格采用ICEM CFD网格生成器制作，附面层第1层网格高度给定为5.8×10-6m，拉伸比为1.2，网格总点数约为273万，远场长度约为50倍短舱外罩长度。发动机表面、进排气边界网格以及网格中心截面如图7所示，TPS模型仿真参数如表4所示。

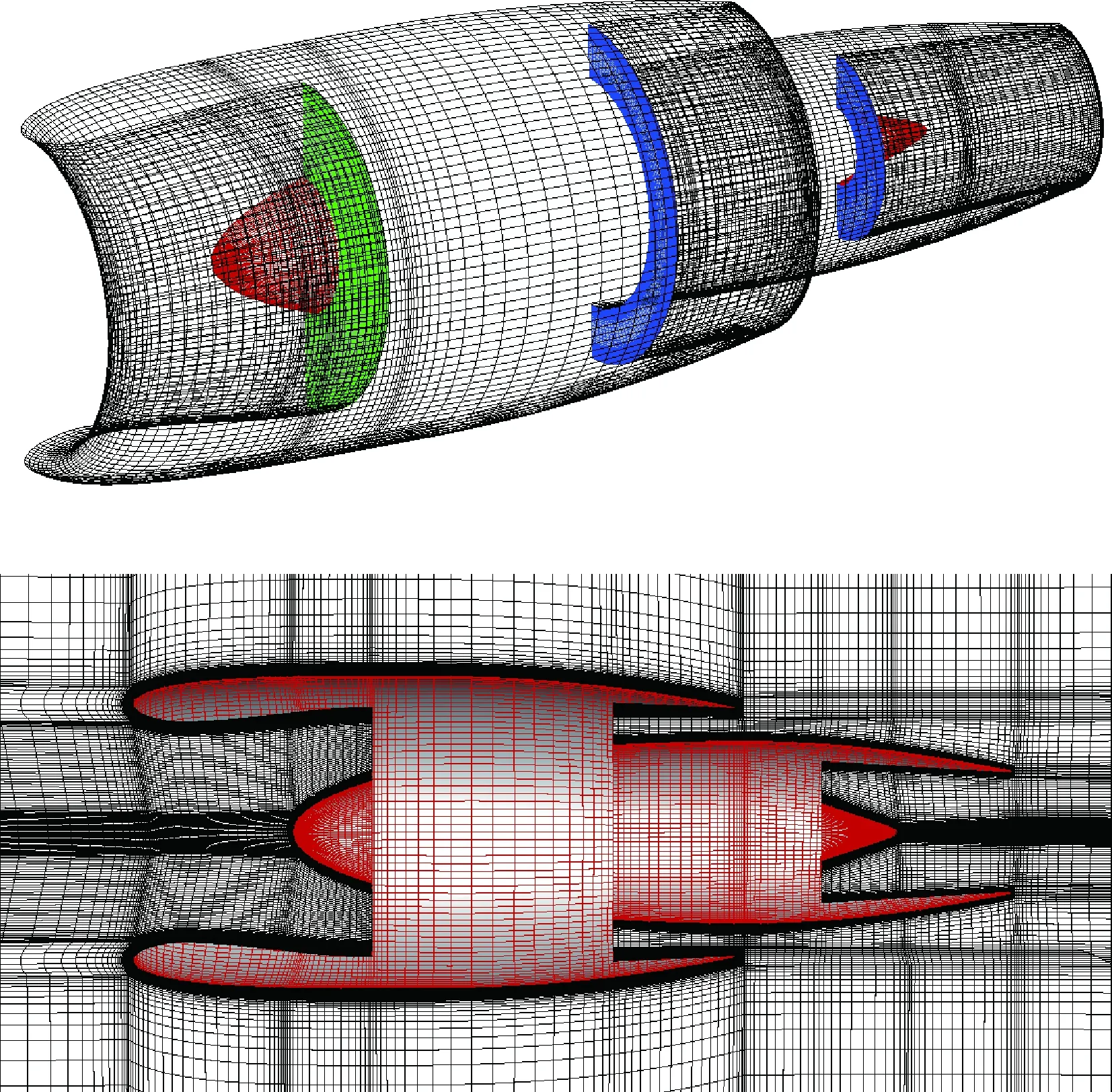
图7 TPS模型计算网格Fig.7 Computational grid of TPS model

表4 TPS模型仿真参数Table 4 Simulation parameters of TPS model

2.2.2 两种动力特性模型比较

图8给出了TPS模型风扇入口处质量流量收敛历史比较，类似于CRUFS模型，两种动力特性模型虽然风扇入口边界条件一样，但不同的外涵边界条件导致模拟初期风扇入口质量流量有些许不同，迭代约2 000步后，两者逐步稳定并趋于一致，很快收敛到目标质量流量8.789 kg/s。图中升力系数收敛历史特征类似风扇入口质量流量，但是升力系数在1 000步以后就趋于稳定。

图8 TPS模型进气口流量收敛速度比较Fig.8 Comparison of convergence rates of mass flow through engine fan of TPS model

正如2.1.2节中所述，验证涡扇发动机动力特性模型正确性的一个重要标准是：排除数值误差影响后，发动机进排气口质量流量是否一致。表5给出了两种动力特性模型计算得到的进排气口质量流量(绝对值)比较。图9给出了短舱中心截面压力系数分布与试验值的比较，结合表5可知，两种动力特性模型计算所得进排气口质量流量、短舱表面压力系数分布一致性较好，与风洞试验也吻合较好，说明两种动力特性模型精度相当，可靠性好。

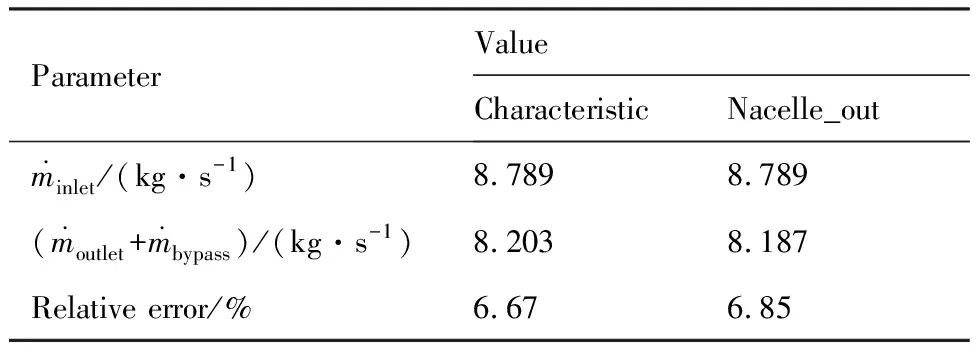
表5 外涵道边界类型对质量流量的影响(TPS)

图9 TPS模型计算得到的压力系数分布比较Fig.9 Comparison of pressure coefficient distributions calculated by TPS model

2.2.3 流场分析

图10给出了TPS模型中心截面处马赫数等值线分布(动力特性模型B模拟结果)，可以看出计算得到的中心截面马赫数分布合理，在外涵道和内涵道出口附近，短舱外气流与外涵道气流、外涵道气流与内涵道气流之间形成较强的剪切流动并且随着流动向下游扩散，3股气流逐渐混合，且马赫数在下游逐步接近来流马赫数。

图10 TPS模型计算得到的马赫数等值线Fig.10 Mach number contours calculated by TPS model

3 某型客机动力特性评估

为验证本文构造的两类动力特性模型的工程适用性，对某型客机带翼吊涡扇发动机模型巡航状态下有无动力、机体/发动机干扰问题进行验证、评估，计算方法和参数与CRUFS、TPS模型一致。

3.1 计算网格及状态

计算网格采用ICEM CFD网格生成器制作，先生成结构化网格，然后转换为非结构网格进行计算。带动力模型需要模拟发动机喷流，因此对发动机附近网格进行了局部修改。除发动机外，其余部件网格拓扑结构与无动力模型网格基本一致，只是对发动机部分拓扑进行了重新构造，其他位置的网格保持与无动力模型基本相同。

无动力模型为C4，网格总点数为2 589.6万；动力模型为C4PN，网格总点数为2 577.5万。远场取100倍平均气动弦长，保证远场的气流不干扰飞机表面的气流，以减少对阻力的影响。机翼前缘网格间距约为0.1%平均气动弦长。后缘分布20个网格点，机翼展向在翼根附近的网格间距约为0.8%半展长，在翼稍附近的网格间距约为0.5%半展长，机身前端和后端为1.5%平均气动弦长。附面层第1层网格高度约为1×10-5m，拉伸比≤1.25。局部计算网格如图11所示，某型客机仿真参数如表6所示。

3.2 两种动力特性模型比较

与CRUFS、TPS模型一样，首先验证发动机进排气口质量流量是否一致，表7给出了两种动力特性模型计算得到的进排气口质量流量(绝对值)的比较。从表7可知，两种动力特性模型计算所得进排气口质量流量一致性较好。

3.3 有无动力计算比较

工程上，评估飞行器机体/发动机干扰问题，一般先计算通气模型无动力流场，进而模拟发动机动力特性，评估发动机动力特性对机体气动特性的影响。因此，本节对比了有无动力对客机气动性能的影响，图12是有无动力模型计算所得机翼2个展向剖面上的压力系数分布曲线(图中b为展长)。

图13是有无动力计算得到的展向剖面(Y=6.18 m)、法线剖面(Z=-2.12 m)马赫数等值线分布比较图，结合图12可知：① 有无动力模型风扇入口处马赫数均约为0.55；② 发动机喷流对机翼上下表面流场影响较大，使得上翼面激波位置前移、强度稍有减弱，发动机唇口激波强度亦减弱；③ 下翼面短舱外气流与外涵道气流、外涵道气流与内涵道气流之间形成较强的剪切流动并且随着流动向下游扩散，3股气流逐渐混合，形成了较强的剪切流动，并一直向下游延伸；④ 外涵道内气流逐步加速，马赫数沿流向逐渐增大，在外涵道出口附近达到最大值，约为0.92，3股气流混合后，马赫数又逐渐降低到接近来流马赫数0.785附近。

图11 某型客机计算网格Fig.11 Computational grid of civil aircraft

表6 某型客机模型仿真参数Table 6 Simulation parameters of civil aircraft model

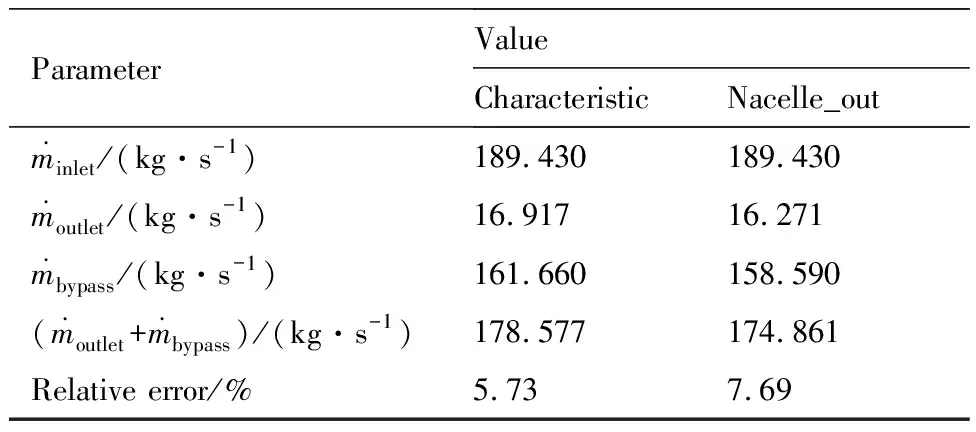
表7 外涵道边界类型对质量流量的影响(C4)

图12 机翼展向剖面有无动力计算得到的压力系数分布Fig.12 Surface pressure coefficient distribution on wing span profiles obtained by models with or without power

图14为有无动力模型计算得到的空间涡黏性系数分布，图中物面采用压力系数分布渲染。翼稍小翼、后缘襟翼滑轨，机身尾部、发动机短舱均不同程度产生了尾涡，尤其是发动机喷流尾涡强度较大且一直向下游延伸，但是对平尾几乎没有干扰。

图13 有无动力模型计算得到的马赫数等值线比较Fig.13 Comparison of Mach number contours calculated by models with and without power

图14 有无动力模型计算得到的空间涡黏性系数分布Fig.14 Eddy viscosity distribution calculated by models with or without power

4 结 论

本文以等熵流动原理为出发点，分析、构造并实现了3类发动机动力边界条件，据此实现了文献中的发动机动力特性模型，同时，基于特征边界思想，建立了一种新的涡扇发动机动力特性模型。采用轴对称超高涵道比涡扇发动机模型CRUFS、轴对称涡轮动力模型TPS对这两种动力特性模型进行了验证，并采用某型客机带翼吊涡扇发动机模型整机进行了工程评估，结果表明：

1) 两种发动机动力特性模型风扇入口质量流量能很快收敛到目标质量流量，且均能很好地模拟涡扇发动机动力效应，计算结果与试验数据吻合较好，验证了本文构造的涡扇发动机动力特性模型的正确性、可靠性以及工程适用性。

2) 两种动力特性模型计算得到的发动机进、排气口质量流量(绝对值)相当，短舱附近机翼表面压力系数分布一致性较好。新构造的模型B更适合于模拟大涵道比涡扇发动机动力特性，且该模型无需事先给定外涵道总温比、总压比等参数，在实际工程中应用更广泛。

3) 翼吊发动机动力特性(喷流)使机翼上表面激波位置前移、强度稍有减弱，发动机唇口激波强度亦减弱，对下表面远离短舱位置(翼根、翼稍)的影响较小。