小剪跨比碳纤维布抗剪加固梁的有限元分析
2019-01-23胡铖玥杨鹏飞李伟文
胡铖玥,杨 泳,杨鹏飞,李伟文,邢 锋
深圳大学土木工程学院,广东省滨海土木工程耐久性重点实验室,广东深圳 518060
在过去20多年里,外贴纤维增强复合材料(fiber reinforced polymer, FRP)对钢筋混凝土(reinforced concrete, RC)构件进行抗剪加固已经成为了一种常用的加固方法. 在对FRP抗剪加固的研究中,有限元分析法是一种常用的手段. 21世纪以来,许多学者开始通过考虑不同的混凝土材料本构、引入合理的FRP-混凝土黏结界面本构、开发适当的界面黏结单元等手段建立了多种FRP抗剪加固RC梁的有限元模型. GODAT等[1]通过拉伸硬化的方法来模拟混凝土的受拉行为,使用固定弥散裂缝模型来模拟混凝土开裂行为,该模型考虑了开裂后材料剪切刚度的折减,并间接地将钢筋的销栓作用考虑在内,取剪切保留因子为定值0.5,尽管模拟所得加固梁的荷载-挠度曲线与实验相当吻合,但是开裂后大多数构件模型的刚度明显要大于实验观测. 类似的现象同样出现在采用了固定的剪切保留因子的拉伸硬化模型的研究中[2-4]. GODAT等[5-6]分析了尺寸效应、剪跨比、配箍率和配布率等参数对模拟结果的影响. LU等[7]提出黏结滑移模型模拟FRP与混凝土的黏结界面,钢筋-混凝土界面仍为刚性黏结,该模型能较好地模拟出FRP剥离现象,且预测的荷载-位移曲线和FRP条带应变分布均与试验值较吻合,反映了目的参数对模拟结果的宏观影响. 但由于混凝土开裂后其剪切刚度的退化定义以及钢筋-混凝土的黏结界面考虑不够恰当,且采用固定弥散裂缝模型模拟混凝土开裂,故对混凝土梁剪切裂缝发展的预测尚不够精确. CHEN[8]使用ABAQUS软件建立较精细的有限元模型,分别考虑FRP、钢筋与混凝土界面的黏结关系,使用与裂缝带模型相结合的转动弥散裂缝模型,裂面剪力传递系数采用以混凝土抗拉应变为变量的方程来代替常数. 该模型预测出的荷载-位移曲线、裂缝图、FRP条带上的应变分布均与试验值较吻合. 但由于裂面传递系数的关系,该模型仅适用于剪跨比为2.5以上的较大剪跨比FRP抗剪加固梁. 徐文冰[9]基于混凝土塑性损伤理论对FRP抗剪加固梁使用ABAQUS进行了分析,所建模型针对混凝土受拉和受压方面采用了多种损伤本构进行正交建模分析,FRP-混凝土界面本构则采用LU等[7]提出的黏结滑移模型,考虑钢筋-混凝土界面的黏结滑移关系. 该模型能较好地模拟出与实验值较为吻合的荷载挠度曲线,并给出了FRP条带应变分布和发展图,分析了条带发生剥离的过程. 但是建立的试验梁剪跨比仍属于中大剪跨比范围,且未对全包裹加固梁进行建模分析.
为了对较小剪跨比的外贴 U 型碳纤维布抗剪加固梁的剪切性能进行较全面的数值模拟和分析,本研究使用ATENA软件,对剪跨比为1.5的未加固梁、U型FRP抗剪加固RC梁进行有限元模型分析,并利用较小剪跨比无腹筋RC梁[10]验证该模型的有效性和普适性.
1 有限元模型验证
1.1 试验介绍
本研究选取文献[10]采用的小剪跨比无腹筋RC梁,建立有限元模型. 混凝土梁的配筋信息见图1. 其中,l为非加固区梁的长度;l′为非加固区有效长度;a为加固区宽度;a′为非加固区宽度;P为荷载.梁的长度为1 450 mm,宽度为190 mm,高度为320 mm,剪跨比为2.00,真实剪跨比为1.70. 梁受拉区域配有2根Φ26 mm的钢筋,混凝土保护层厚度为37 mm,未配置箍筋以及受压纵筋,加载端以及支座区各有30 mm厚的金属垫块,以防止应力集中和混凝土被压碎.
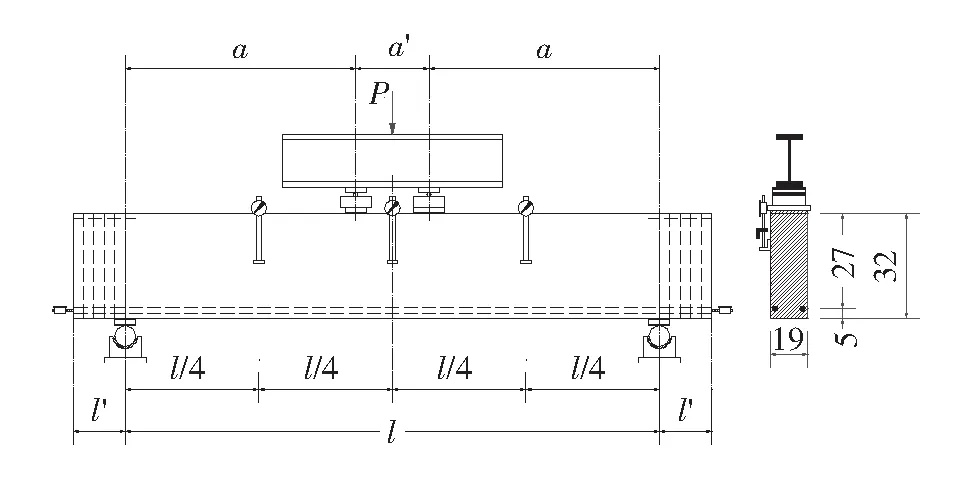
图1 梁的基本尺寸信息[10](单位:mm)Fig.1 Specimen’s configuration details[10](unit:mm)
1.2 模型建立及相关材料参数取值
本研究混凝土采用ATENA自带的SBETA混凝土材料本构. SBETA是基于混凝土断裂能理论并引入损伤概念所形成的一种材料模型,该材料模型几乎涵盖了混凝土受拉受压方面的所有重要特征. SBETA模型是在KUPFER[11]提出的双轴破坏准则以及DARWIN等[12]提出的等效单轴应力-应变曲线的基础上建立的. 在混凝土受拉情况下的应力应变关系中,根据修正的等效单轴应力-应变曲线,混凝土在受拉开裂前呈线弹性,受拉开裂后是基于裂缝带理论和裂缝张开法则[13]的综合考虑. 混凝土受压在峰值应力之前,采用欧盟规范[14]所建议的公式计算:
(1)
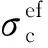
钢筋材料为完全弹塑性材料,应力应变曲线采用双线性,其收敛性能表现良好,分析结果具备较高的精度. 大量实验研究证明,FRP材料在达到其极限拉应力之前是线弹性的,达到极限拉应力即呈现为脆性拉断[5-8]. 故FRP材料采用的增强材料,应力应变曲线采用完全线弹性,当其应力超过极限应力时,其值将变为零.
对于FRP-混凝土界面材料,本研究采用ATENA软件内置的Bond for Reinforcement黏结材料模型.由于LU等[7]提出的黏结-滑移模型能够较好地反映FRP-混凝土黏结界面的力学行为,本研究采用该本构模型定义FRP-混凝土黏结界面,
(2)
(3)
τmax=α1βwft
(4)
(5)

在模拟FRP抗剪加固RC梁时,较少考虑钢筋混凝土界面黏结滑移行为,但是CHEN等[8-9]认为,钢筋混凝土界面黏结滑移行为对模拟结果有较大影响. 由于该界面的力学行为会影响裂缝的开展及分布,且设定为刚性黏结会高估模型的刚度和极限载荷. 对于钢筋与混凝凝土界面,本研究采用的钢筋混凝土界面黏结滑移本构为[15]
由于波特一致性系数只是给出了总体的一致性比较,为了分别在内容主题维度和认知层次维度上对大纲标准和7套试卷中的数学学科知识题进行比较,研究者在下文将矩阵的数据信息,绘制为条状图,从而在图中可以清晰的看出被研究者在内容上的侧重主题与认知上的侧重水平,呈现更为明确的信息.
(6)
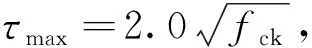
本研究采用ATENA软件分别对试验梁进行二维建模. 混凝土单元采用实体单元,钢筋单元和FRP单元均为桁架单元,长度为10 mm,网格划分为四边形. 每个步骤施加0.1 mm的位移荷载. 图2给出了有限元模型所预测的荷载-挠度曲线. 由图2可见,模型开裂前走势基本与实验结果一致,开裂后模型预测荷载-挠度曲线与实验结果略有差异,但也基本吻合,加载至极限荷载时,挠度值与实验结果也极为相近. 表1给出了有限元模型所预测的极限荷载及对应的跨中挠度值与实验结果的对比. 由表1可知,有限元模型对跨中挠度值的预测结果良好,误差控制在5%以内. 综上所述,有限元模型能够得出与无腹筋梁实验结果相当吻合的荷载-挠度曲线.
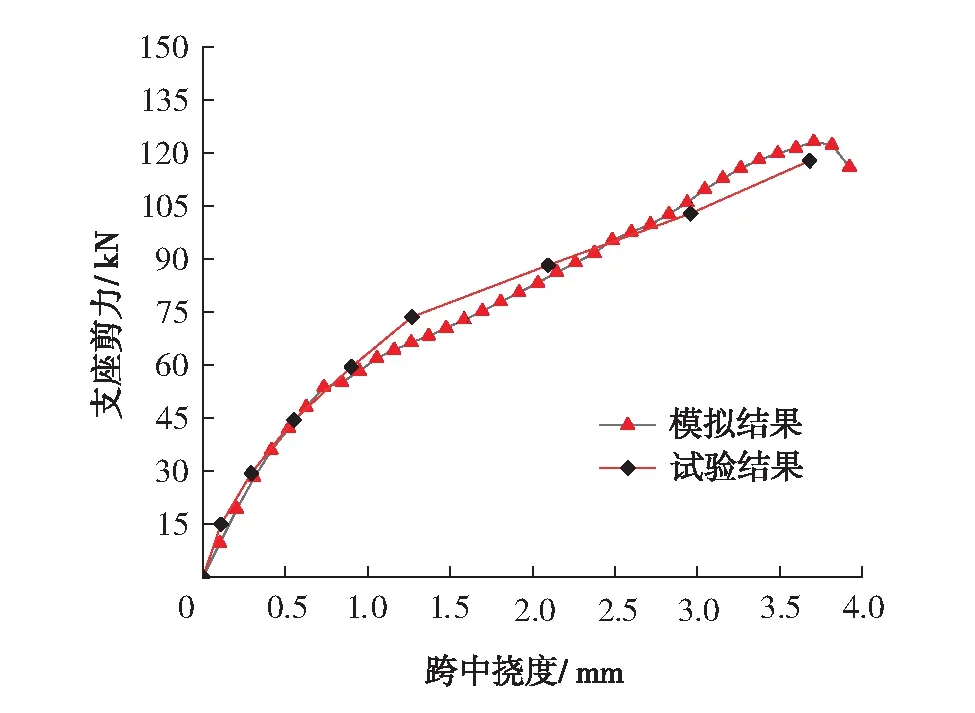
图2 试验梁的荷载位移曲线Fig.2 Load-deflection relationship of beam
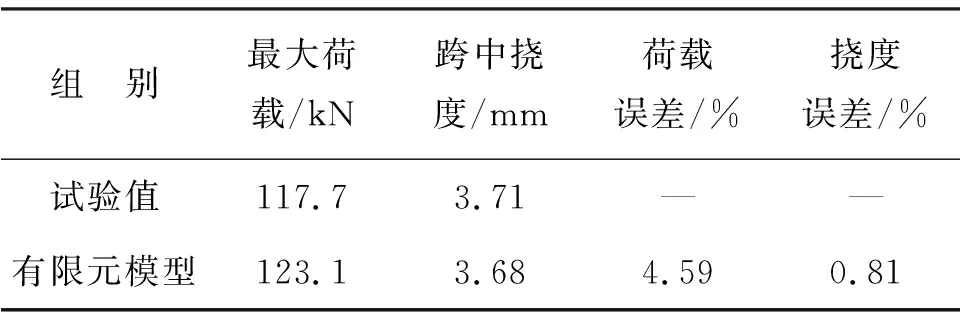
表1 极限荷载及对应跨中挠度值Table 1 The ultimate load and the corresponding midspan deflection
图3给出了有限元模型在极限状态下的裂缝分布与实验所观测到的裂缝分布对比. 由图3(b)和(c)可见,斜裂缝始于弯裂缝的倾斜发展,并蔓延至加载端,最终加载端右侧混凝土出现裂缝,随后该区域混凝土被压碎,构件丧失承载力. 对比图3(a)与(b)、(c)可见,有限元模型所预测得到的裂缝分布图与实验观测较为吻合,且主要斜裂缝倾斜角度与实验观测基本一致.

图3 极限荷载状态下的裂缝分布Fig.3 Crack patterns at ultimate state
2 FRP抗剪加固梁的有限元模拟
2.1 试验介绍
选取LI等[15]试验所用的2根试验梁B2C和B2U进行有限元分析. 2根试验梁分别为对照RC梁和U型包裹FRP抗剪加固RC梁,剪跨比均为1.5,试件尺寸以及配筋信息见表2,其几何简图及有限元几何模型见图4.其中,a和c分别为两端离支座的距离.

表2 各试验梁具体几何尺寸及配筋信息[15]Table 2 Geometrical dimensions of the tested beams[15]
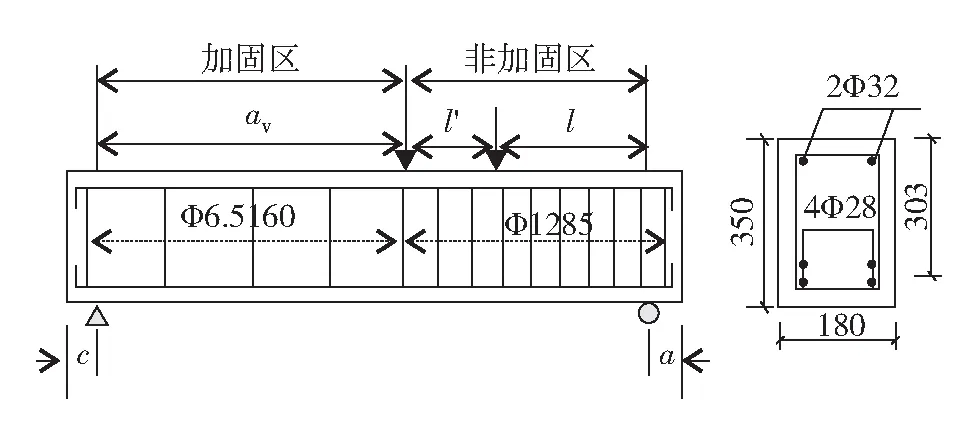
图4 试验梁立面图和剖面图Fig.4 Axial strain profiles along the beam length for strips
2.2 有限元模型
采用的材料本构与材料单元与1.2节一致. 由于实验中为4点对称加载,为节省计算量,选取一半结构进行建模,图5是两根梁的几何模型简图.
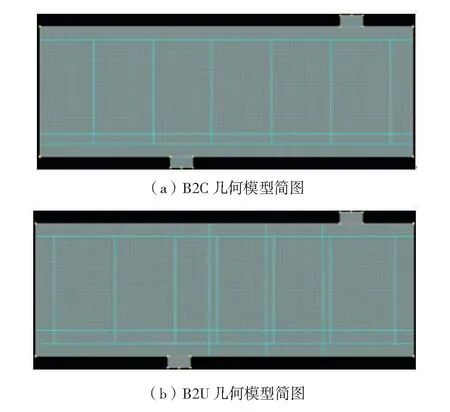
图5 有限元几何模型简图Fig.5 Sketch of finite element model
3 有限元模拟结果和分析
图6(a)和(b)分别为B2C和B2U有限元模拟所得的剪力-跨中挠度曲线及其与实验结果的对比. 由图6(a)和(b)可见,模型预测曲线与实验曲线的前期走势区别较大,这可能是由于实验预加荷载过小,使得构件前期处于应力松弛状态,从而导致试件在加载初期未能达到构件实际刚度,以至于实验采集所得数据存在误差;两种曲线后期斜率及走势逐渐吻合,说明这种误差在充分的加载过程中逐渐被消除. B2C和B2U的有限元模拟得到的最大剪力值分别为299.8 kN和326.4 kN,对应的跨中挠度值都为2.4 mm,与实验值吻合较好.
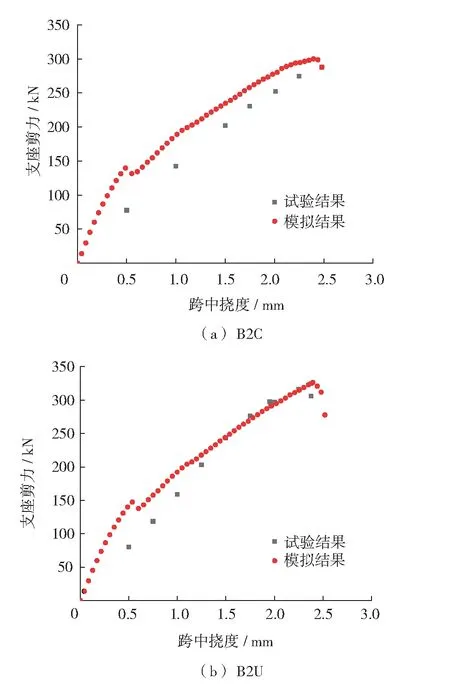
图6 实验剪力-跨中挠度曲线与有限元模拟结果对比Fig.6 Load-deflection relationships for the specimen
图7给出了B2U有限元模拟所得到的S1条带和S2条带在剥离瞬间的黏结应力变化. 在跨中挠度达到2.443 mm时,S1条带在距离梁底高度300~350 mm段黏结应力减小为0,对应的界面滑移量则骤增,可判断该区域S1条带达到完全剥离. 在跨中挠度达到2.521 mm时,S2条带在距离梁底200~250 mm部分的黏结应力减小为0,对应的界面滑移量也有较大增量,可判断该区域S2条带已发生剥离,根据裂缝分布图可判断该区域条带与剪切裂缝相交,由于S2条带在裂缝上端仍有近100 mm的黏结长度,故有限元模拟所得条带应力无法瞬间传递到上端,导致上端条带与裂缝处条带同时剥离. 根据实验观测,S2条带裂缝上端的部分是由于胶层脱落所导致的脱离,而非典型的界面剥离,因此有限元模拟中S2条带部分剥离属合理破坏模式. 2条带剥离模式与实验基本符合.
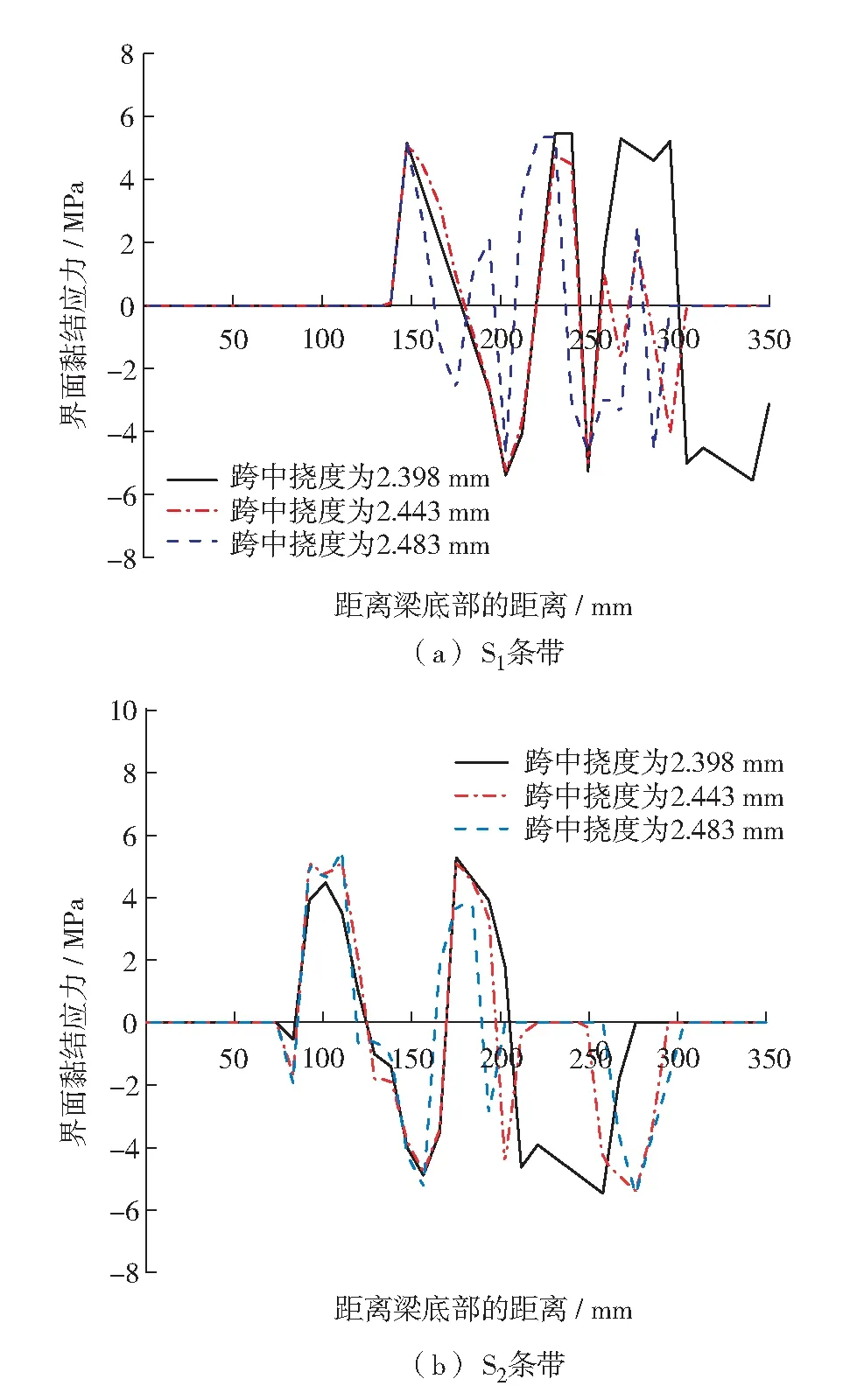
图7 FRP条带S1和S2剥离瞬间黏结应力的变化Fig.7 FRP strips S1 and S2 debonding stress
为研究试件裂缝的发展和分布,图8给出了实验所观测到的梁试件在极限荷载状态下的裂缝分布.由于外贴条带的存在,B2U的裂缝张开宽度明显比B2C要小,尤其是非主裂缝,不仔细观察几乎难以发现. 荷载增加过程中,微裂缝先出现在相对靠近跨中的区域,箍筋和条带开始发挥作用,混凝土内部应力重新分布,主斜裂缝逐渐出现在梁下端近支座位置. 由于存在纵筋销栓的作用,裂缝与梁底间尚有一段距离. 随着荷载的增大,主斜裂缝逐渐朝加载端方向发展,同时梁近加载端上方也出现了微裂缝. 继续加载,裂缝张开宽度增大,构件不时发出脆响,条带应变增长迅速,微裂缝逐渐在加载端附近集结,最终导致该部分混凝土被压碎,条带同时迅速发生剥离,构件彻底失效.
图9给出了有限元模型所得到的起始开裂、中期裂缝和最终裂缝分布. 当剪力值增大至137.9 kN时,2条长短不一的剪切微裂缝同时出现在梁试件偏下部位置,荷载-挠度曲线有一个明显的下降,可见开裂导致构件内部应力重新分布,箍筋和条带开始发挥作用. 随着荷载的继续增加,当剪力值达到204.1 kN时,主要剪切裂缝已逐渐向加载端方向蔓延,同时加载端附近梁上端出现一条微裂缝. 当剪力值达到326.4 kN即极限荷载时,加载端左侧混凝土微裂缝集结,导致该部分混凝土被压碎,同时FRP条带S1发生完全剥离,S2发生部分剥离.有限元模拟裂缝发展及分布与实验观测基本一致.

图8 试件在极限荷载状态下的实测裂缝分布(B2U)Fig.8 Experimental crack patterns at ultimate state (B2U)

图9 有限元模拟加载过程中的裂缝发展及分布Fig.9 FE crack patterns at ultimate state
钢筋混凝土梁的受剪过程同时存在“梁作用”和“拱作用”的双重受剪机制,而较小剪跨比梁的受剪过程主要由拱作用主导. 在图10中可以看到明显的拱形,进一步验证了拱作用对小剪跨比梁的影响,说明ATENA有限元模型能较好地模拟小剪跨比梁. 由此可见,本研究建立的有限元模型预测的荷载挠度曲线、裂缝发展分布等主要力学性能均与实验结果较为吻合,但是由于小剪跨比梁抗剪加固研究成果较少,模型的普适度尚待进一步验证.
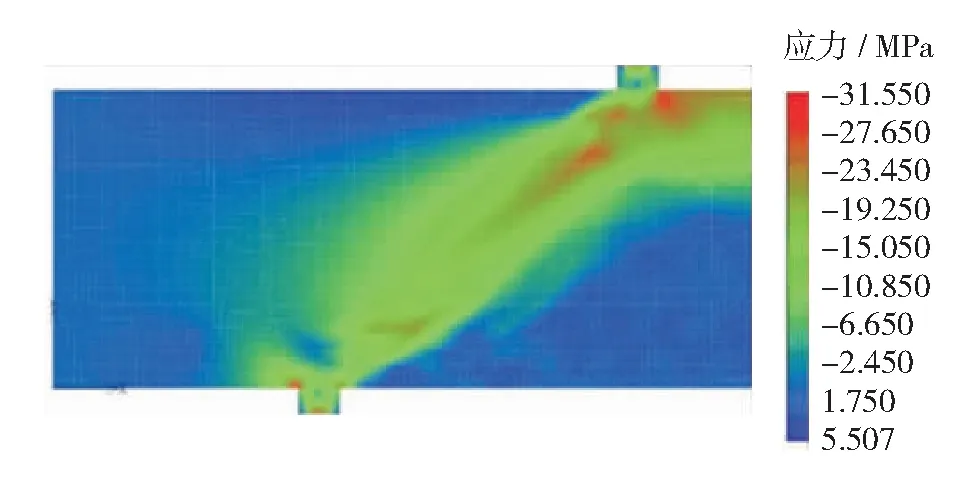
图10 应力云图(B2C)Fig.10 Stress cloud charts(B2C)
4 结 论
本研究对加固梁的抗剪性能及开裂破坏行为进行了有限元分析,可知:
1) 将基于断裂损伤理论与RCM相结合的混凝土本构应用于较小剪跨比FRP抗剪加固RC梁,所建立的有限元模型既能准确预测无腹筋情况下的未加固RC梁和U型FRP抗剪加固RC梁开裂后的荷载-挠度曲线,也能有效预测有腹筋情况下的未加固RC梁和U型FRP抗剪加固梁开裂后的荷载-挠度曲线,证明该混凝土本构在模拟FRP抗剪加固RC梁开裂后的裂缝发展分布及构件的非线性力学行为方面,具备独特的准确性.
2) 在剪跨比较小的情况下,FRP对于U型加固RC梁的抗剪贡献较为有限,因构件破坏往往由混凝土压碎控制,但是FRP会通过限制拱腹混凝土的开裂间接提高拱腹混凝土的抗压性能.当然,这种提升比较有限,且对构件的变形有一定影响.此外,由于构件剪跨比偏小,FRP-混凝土黏结界面剥离或FRP拉断的现象往往发生在极限荷载达到瞬间或极限荷载之后,且部分条带不能发生完全剥离,FRP抗拉强度高的优势在这种情况下往往得不到充分发挥.
3) 对黏结界面真实受力性能的模拟至关重要,选择合理的界面黏结滑移本构,才能准确模拟混凝土的应力状态,分析混凝土裂缝的发展及后续走向. 而黏结界面的不合理模拟甚至会改变构件的最终破坏形态.
