大规模数据集聚类算法的研究进展
2019-01-23何玉林黄哲学
何玉林,黄哲学
1)深圳大学计算机与软件学院,广东深圳 518060;2)深圳大学大数据系统计算技术国家工程实验室,广东深圳 518060
聚类是一种挖掘数据内在相似性的无监督机器学习技术,是一个将数据集划分成若干数据子集的过程[1].每个数据子集是一个簇,簇内样本彼此相似,不同簇间的样本不相似.通常情况下,样本的相似性使用欧氏距离、马氏距离、曼哈顿距离、切比雪夫距离、余弦相似度、皮尔森相似度、Jaccard相似度,以及概率密度等来刻画.聚类技术在实际生活中已被广泛应用,例如商业活动中的客户分群[2]、生物信息学中的基因序列分类[3]、互联网中的垃圾邮件识别[4],以及电力市场中行业用电行为分析[5]等.在过去几十年间,针对不同类型中小规模数据集的聚类算法在聚类精确度方面已取得了重要的突破.经典的聚类算法包括针对连续属性值的k-means算法[6]及其模糊版本Fuzzyc-means算法[7]、针对离散属性值的k-modes算法[8-9]及其模糊版本Fuzzyk-modes算法[10]、针对混合属性值的k-prototypes算法[8]及其模糊版本Fuzzyk-prototypes算法[11]、基于层次的AGNES和DIANA聚类算法[12]、基于密度的DBSCAN(density-based spatial clustering of applications with noise)聚类方法[13]以及基于网格的STING(statistical information grid)聚类算法[14]等.
随着大数据时代的到来(2013年被称为“大数据元年”),数据的采集和存储变得相对容易和便捷,Gbyte级乃至Tbyte级存储的大规模数据集层出不穷,通常这些数据集的数据量会超出单个计算节点的内存容量,导致数据无法被加载到内存.同时,针对这些大数据集的聚类任务也应运而生.直接套用上述针对中小规模数据集的聚类算法往往不能获得令人满意的应用结果,主要缺陷表现为较高的计算复杂度.以SPODS数据集为例,包含29万条15个属性的样本,数据量大约为450 Mbyte,使用Fuzzyc-means聚类算法将其聚成3类,在配置为单核i7-2.80 GHz CPU和8 Gbyte内存的64 bit 的PC机上运行需时约4 min[15].依此推断,当人们使用Fuzzyc-means聚类算法去处理Gbyte级和Tbyte级大规模数据时,运算时间将令人难以接受.因此,专门针对大规模数据集的聚类算法研究成为当前机器学习领域的重要任务之一.
大数据分析的核心是大数据的可计算问题.本文从大规模数据集的可计算性入手,对目前串行和并行计算环境下专门用于处理大规模数据集的聚类算法进行详尽评述和分析,同时给出未来大规模数据集聚类算法设计思路与应用前景的思考和讨论.图1给出了本综述的组织结构.
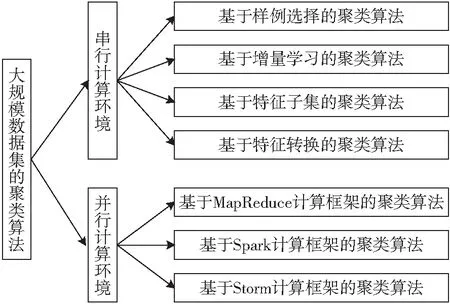
图1 本综述的组织结构Fig.1 Organization of the review
1 大数据串行聚类算法
串行计算(sequential computing)指程序在单个处理器上被顺序执行.在此,我们将对串行计算环境下适用于大规模数据集的聚类算法进行阐述.这类算法的实质是对原始数据集的样本空间或是特征空间进行压缩,并在缩减后的数据集上进行聚类.
1.1 基于样例选择的聚类算法
基于样例选择的聚类算法的主要特点是从原始数据集中挑选出部分样本进行聚类.
1998年,BRADLEY等[16]提出一种具有可伸缩性的k-means(scalablek-means, ScaleKM)聚类算法.首先,将原始数据集划分成若干个数据子集,每个子集又被分成丢弃集、压缩集和保留集.之后,在每个子集的压缩集上训练k-means算法,并使用全部保留集对这些k-means算法进行优化.ScaleKM不需要将原始数据集读入内存,即可实现对大规模数据集(含13 711个64维的样本)的聚类.
2000年,PALMER等[17]提出基于密度偏差的抽样方法,并将其用于利用层次方法的平衡迭代规约和聚类(balanced iterative reducing and clustering using hierarchies,BIRCH)算法[18]的训练.密度偏差抽样根据单个样本在整个数据集中的分布密度进行抽样,样本被抽中的概率与样本的分布密度直接相关.首先,基于密度偏差抽样选取训练集,再在抽样上训练BIRCH算法,该方法降低了算法的训练时间.实验结果表明,基于偏差抽样的BIRCH算法能处理含2×105个50维样本数据的聚类问题.其他基于密度偏差抽样聚类方法的研究见文献[19-21].
2009年,张驹等[22]提出基于Hash函数抽样的HSCS聚类算法,专门用于处理流数据的聚类问题.该算法首先使用Hash函数对进入滑动窗口的数据流进行抽样,再将抽样数据转化为静态数据,并使用围绕中心点的划分(partitioning around medoid, PAM)算法[23]进行聚类.实验结果表明,HSCS在处理大规模数据(含15 000个样本,30个簇)的聚类问题时,表现优于经典的CluStream算法[24].文献[25]详细介绍了使用基于抽样的聚类方法处理大规模流数据的研究.
2013年和2014年,王秀华[26]和罗军锋等[27]相继提出基于随机抽样的k-means聚类算法.这两种算法的共同点是首先对大规模数据进行随机抽样,同时设计相应的聚类有效性指标,再在样本上训练k-means算法,并验证聚类的有效性,若有效,则训练停止;否则,重复上述过程.这两种算法的主要差别体现在使用了不同的随机抽样方法.实验结果显示,前者能够处理含30 000个9维样本数据集的聚类问题,后者可处理含8 124个23维样本数据集的聚类问题.
最近,CHEN等[28-29]提出了两种针对大规模数据集的谱聚类(spectral clustering)[30]算法,通过利用小规模且有代表性的表达矩阵来训练谱聚类算法.其中,小规模表达矩阵的获得分别采用可扩展的规范切割法(scalable normalized cut, SNC)和快速规范切割法(fast normalized cut, FNC).实验结果证明,基于SNC和FNC的谱聚类算法具备处理大规模数据的潜力.
1.2 基于增量学习的聚类算法
此类算法在增量学习框架下完成对聚类算法的训练.先基于部分数据训练聚类算法,再通过增删数据动态地更新聚类结果.具有代表性的增量学聚类算法研究包括:
最早的增量聚类算法是1998年由ESTER等[31]提出的增量DBSCAN算法.该算法中,增量与原DBSCAN算法是等价的(增量算法与非增量算法的聚类结果保持一致).这也是增量聚类算法DBSCAN较其他类型增量聚类算法的最大优势[32].该算法的关键步骤是有效处理增删数据对当前聚类结果的影响. 2004年,黄永平等[33]对传统的增量DBSCAN算法进行了改进,提出批量增量DBSCAN算法,即对数据的增删是批量进行的.其他关于增量DBSCAN算法的研究可参见文献[34-36].PHAM等[37]提出增量k-means聚类算法,包含2个阶段:第1阶段是传统的k-means算法训练过程,第2个阶段是增量训练k-means算法的过程,即新旧聚类结果的融合.之后,CHAKRABORTY等[38]提出了一种核心思想与PHAM等的方法类似的增量k-means聚类算法.
其他形式的增量聚类算法还包括高小梅等[39]提出的增量k-Medoids聚类算法、王洪春等[40]提出的增量模糊c-均值聚类算法,以及ZHAO等[41]提出的增量CFS聚类算法等.关于增量聚类算法研究的介绍可参见文献[42].
1.3 基于特征子集的聚类算法
基于特征子集的聚类算法是一类尝试在数据集的若干特征上发现类簇的算法,包括两种形式:第1种是基于特征选择(feature selection)的聚类算法,即从原始特征空间选择若干特征进行聚类;第2种是基于特征子空间(feature subspace)的聚类算法,即将原始数据空间划分成若干子空间(或称网格)分别聚类.无论哪一种形式,目的都是通过在数据集的部分特征上完成对聚类算法的训练,提高聚类算法处理高维数据的能力.
基于特征选择聚类算法的重点在于无监督的特征选择.特征选择算法的研究是机器学习和数据挖掘领域的热点[43-44],在此不再赘述.基于特征选择的聚类算法先从数据集的特征集合中选择若干特征,再提取特征子集的数据训练聚类算法.最新的研究工作见李斌等[45]提出的NGKCA (novel globalk-means clustering algorithm)和杜世强[46]提出的图正则化紧凑低秩表示(graph regularized compact LRR, GCLRR)算法.前者采用谱聚类算法对原始数据集进行降维和归一化,后者采用矩阵分解方法对原始数据集进行维数约简.
基于特征子空间的聚类算法代表性的研究成果有:1998年AGRAWAL等[47]提出一种基于网格的CLIQUE聚类算法,用于发现子空间中高密度的簇.该算法依靠两个参数把整个数据空间划分成若干不重叠的网格单元:一是网格步长,用以确定数据空间的划分;二是密度阈值,用以定义密集的网格.该算法依次完成对密集网格的判断,将相邻密集网格合并为同一个簇.CHENG等[48]提出基于信息熵的ENCLUS聚类算法,该算法对CLIQUE算法进行了轻微改进,即基于信息熵判断网格的有效性,只在有效的网格中使用现有的聚类算法完成对数据的聚类.NAGESH等[49]提出MAFIA(merging of adaptive finite intervals)聚类算法,将每个特征上分布密度相似的数据段进行合并,并把可变网格的思想引入CLIQUE算法中.KAILING等[50]提出SUBCLU(dersity-connected subspace clustering)聚类算法,通过将DBSCAN 聚类算法中密度连接的概念扩展到子空间中,并在子空间中通过DBSCAN聚类算法产生聚类结果.HUANG等[51]提出一种基于特征加权的k-means算法W-k-means.JING等[52]、CHEN等[53]和赵鹤[54]分别提出W-k-means的改进算法EWKM(entropy weightingk-means)、FG-k-means和ENLDA-BFGKM.不同于先前的硬子空间聚类(hard subspace clustering)算法,W-k-means系列算法为软子空间聚类(soft subspace clustering)算法,即特征与簇之间不再是“非0即1”的隶属关系,而是使用区间[0, 1]的实数表征这种隶属关系.其他关于特征子空间聚类方法的研究可参见文献[55-58].
1.4 基于特征转换的聚类算法
基于特征转换的聚类算法的主要特点是对数据集的原始特征空间进行转换,通常是将高维数据转换为低维数据(也存在低维向高维转换的情况),然后利用现有的聚类算法对转化后的数据集进行聚类分析.
主成分分析(principal component analysis, PCA)[59-60]是一种重要的数据降维方法,它通过正交变换将一组存在相关性的特征转换为一组线性不相关的特征,转换后的这组特征叫做主成分.基于PCA的聚类算法是典型的特征转换式聚类算法.2001年,YEUNG等[61]对基于PCA的聚类算法进行了研究,并在基因表达数据上对聚类算法在特征转换前后的表现进行了实验验证.2004年,DING等[62]研究了基于PCA的k-means聚类算法,分别对1×103维特征转换成40、20、10、6和5维之后的k-menas算法表现进行了验证.2010年,ALZATE等[63]研究了基于加权核PCA的谱聚类算法,在经过加权核PCA处理的数据集上训练多路谱聚类算法.其他通过PCA降低聚类算法复杂度的研究还可查阅文献[64-67].
近年来,随着深度学习(deep learning)[68]技术的普及,基于深度学习的聚类算法也开始得到业内人士的关注.2016年,原旭等[69]提出一种基于AutoEncoder的增量式聚类算法ANIC,首先,利用自编码器学习原始数据的高维空间特征;然后,对特征进行低维整合,得到原始数据集的压缩形式;最后,使用k-means算法和模糊c-means算法进行聚类.杨琪[70]也针对基于深度学习的聚类关键技术,提出基于深度信念网络的模糊c-means聚类算法DBNOC(deep belief networks oriented clustering),先利用深度信念网学习大规模数据集的深度特征表示,再使用模糊c-means算法进行聚类.
2 大数据并行聚类算法
并行计算(parallel computing)是指程序在多个处理器上被并发执行.在此将介绍并行计算环境下适用于大规模数据集的聚类算法.这类算法的实质是对大数据的“分而治之”,在分布式的计算框架下通过不同的计算范式完成对聚类算法的训练.
2.1 基于MapReduce计算框架的聚类算法
MapReduce是由Google公司提出的一种面向大规模数据集处理的并行计算模型[71],其核心是数据划分和计算任务调度,即Hadoop分布式文件系统(Hadoop distributed file system, HDFS)自动将一个待处理的大数据划分为多个数据块,每个数据块对应一个计算任务,并自动调度计算节点(Map节点或Reduce节点)来处理相应的数据块,同时负责监控这些节点的执行状态,负责Map节点执行的同步控制.针对同一类型的聚类算法,在MapReduce框架下不同并行化策略的主要差别体现在Map函数和Reduce函数的设计上.下面介绍基于MapReduce框架的聚类算法研究的代表性工作.
2.1.1 基于MapReduce的k-means算法
2009年,ZHAO等[72]首次基于MapReduce框架设计实现了并行k-means聚类算法PKMeans(parallelk-means).结果表明,PKMeans在含4个计算节点的集群上具备处理8 Gbyte大规模数据聚类问题的能力(加速比约为3.5).2011年,江小平等[73]基于MapReduce框架设计了基于10个计算节点的并行k-means聚类算法.2014年,CUI等[74]基于MapReduce框架设计了一种消除迭代相关性的k-means聚类算法,并在拥有16个计算节点的集群系统上,证实了算法具有处理含4 296 075 259个9维样本的大规模数据集聚类问题的能力.
2.1.2 基于MapReduce的模糊c-means算法
2013年,虞倩倩等[75]设计了基于MapReduce框架的并行模糊c-means算法.其中,Map函数负责计算每个样本到中心点的隶属度,Reduce函数负责根据Map函数的中间结果计算出新的聚类中心,供下一轮的MapReduce任务使用.实验结果表明,在含有10个计算节点的集群系统上,并行模糊c-means算法在处理1 Gbyte左右大规模数据聚类问题时的加速比约为2.0.2015年,LUDWIG[76]从可扩展性角度出发,设计了基于MapReduce的模糊c-means算法MR-FCM(MapReduced-based fuzzyc-means).2016年,LI等[77]设计了基于MapReduce的快速模糊c-means算法MR-FFCM(MapReduced-based fast fuzzyc-means),比MR-FCM在处理2 Gbyte的大规模数据集时的运行时间缩短了约50%.
2.1.3 基于MapReduce的DBSCAN算法
2011年,HE等[78]设计了首个基于MapReduce框架的DBSCAN算法MR-DBSCAN.实验结果表明,该算法在拥有10个计算节点的集群系统上,处理8.4 Gbyte大规模数据集聚类问题时的加速比约为5.0.2014年,NOTICEWALA等[79]设计了基于MapReduce框架的并行增量DBSCAN算法MR-IDBSCAN.同年,KIM等[80]设计了另外一种基于MapReduce框架的DBSCAN算法DBCURE-MR.与MR-DBSCAN相比,该算法能够以批量的形式探测类簇(MR-DBSCAN是逐个探测类簇).实验结果显示,DBCURE-MR拥有比MR-DBSCAN更高的加速比.2018年,王兴等[81]提出了一种基于MapReduce框架的并行增量DBSCAN算法IP-DBSCAN,着重用以解决大数据的弹性划分和聚类簇的判断与合并.
2.1.4 其他聚类算法
其他聚类算法还包括张磊等[82]提出的并行网格聚类算法、张雪萍等[83]提出的并行k-medoid聚类算法、涂金金等[84]的并行层次聚类算法、蔡斌雷等[85]提出的针对流数据的并行聚类算法、杨煜等[86]的并行谱聚类算法,以及张伟鹏等[87]的并行图结构聚类算法等.关于MapReduce框架下高效聚类算法模式设计的工作可参见文献[88-89].
2.2 基于Spark计算框架的聚类算法
Apache Spark[90]是一个基于内存计算的开源集群计算框架,它拥有MapReduce的优点,但优于MapReduce的是中间输出结果可保存在内存中,从而不需要再读写HDFS,因此Spark更适于需要迭代的数据挖掘与机器学习算法.另外,由于采用内存迭代计算,Spark的计算模型可分为多个阶段(MapReduce计算模型只含有Map和Reduce两个阶段).尽管Spark推出时间较晚,但一经问世,就因其在处理大数据计算问题上有独特优势被业界广泛推崇为大数据计算引擎.关于Spark框架下大数据计算与分析的研究进展可参见文献[91-92].
下面给出基于Spark框架聚类算法研究的代表性工作.
2.2.1 基于Spark的k-means算法
2016年,KUSUMA等[93]实现了Spark框架下的智能k-means聚类算法,该算法使用批数据(batch of data)策略替代Spark中的弹性分布式数据集(resilient distributed dataset, RDD),提高了算法处理大规模数据聚类问题的效率.实验结果显示,与未采用批数据策略的Spark实现相比,处理时间缩短了近60%.吴哲夫等[94]在Spark框架下设计了基于非均匀采样原则的并行k-means聚类算法,在含有4个计算节点的集群系统上处理1 265 Mbyte数据的加速比达到4.5左右.2018年,侯敬儒等[95]设计了Spark框架下基于Repartition算子分片加载数据策略的并行k-means聚类算法,有效减少了在大规模数据集上训练聚类算法的时间.徐健锐等[96]利用预抽样和最大最小距离相结合的策略对传统的k-means算法进行了改进,在Spark框架下实现了对改进k-means算法的并行化.如何改善k-means类算法Spark实现效率的研究可参见文献[97].
2.2.2 基于Spark的模糊c-means算法
2015年,梁鹏[98]实现了Spark框架下可扩展的核化模糊c-means算法scalable KFCM.该算法引入了核函数的思想,通过将原始空间的样本映射到高维空间之后再进行数据划分,提高并行模糊c-means算法的聚类能力.2016年,王桂兰等[99]设计了Spark框架下基于自定义缓存敏感矩阵操作的并行模糊c-means算法Spark-FCM,最大程度降低计算节点之间的数据移动,保证了聚类算法性能与数据量之间的线性关系.BHARILL等[100]设计了一款Spark框架下基于可扩展随机抽样的迭代优化模糊c-means算法SRSIO-FCM.
2.2.3 基于Spark的DBSCAN算法
2015年,CORDOVA[101]首次实现了Spark框架下的DBSCAN算法RDD-DBSCAN.2016年,LULLI等[102]实现了Spark框架下针对任意数据集的可扩展DBSCAN算法NG-DBSCAN.2017年,金都[103]设计了基于单节点Spark平台的并行DBSCAN聚类算法.黄明吉等[104]设计了Spark框架下DBSCAN算法的有向无环图(directed acyclic graph, DAG),最大限度地降低Shuffle频率和数据量.实验结果显示,在处理3×106个样本的聚类问题时,并行DBSCAN的加速比可达到1.6.2018年,朱子龙等[105]通过设计高效的Spark算子和实现对寻找核心数据密度可达点过程的并行化,完成了对Spark框架下并行DBSCAN算法的开发.
2.2.4 基于Spark的谱聚类算法
2017年,吴稀钰[106]针对具体的应用(快速存取记录器QAR数据),设计了基于Spark图计算组件GraphX、HDFS和分布式数据仓库Hive的首个并行谱聚类算法.2018年,朱光辉等[107]设计了基于Spark框架的大规模并行谱聚类算法SCoS,采用了基于多轮迭代的并行计算方式、基于ScaLAPACK的特征向量并行化求解、基于稀疏化的矩阵表示和存储、Laplacian矩阵乘法优化等关键技术.
2.2.5 其他聚类算法
其他聚类算法还包括邱荣财[108]的CURE(clustering using respresentative)聚类算法、JIN等[109]的可扩展层次聚类算法、ZHU等[110]的并行子空间聚类算法、刘小龙[111]的超图聚类算法以及臧兆杰[112]的并行k-medoids聚类算法等.
2.3 基于Storm计算框架的聚类算法
Apache Storm是一个分布式、高容错的实时大数据处理系统,高度专注流式数据的处理,有时也被称为实时处理领域的Hadoop[113].Storm集群的输入流由喷口(spout)组件管理,spout将数据传送给螺栓(bolt).Bolt要么把数据保存到存储器上,要么把数据传给其他bolt.Storm集群就是在多个bolt之间转换spout传送过来的数据.Storm集群包含两类节点:一个主节点(nimbus)和多个工作节点(supervisors).主节点负责分发任务,工作节点负责执行任务.当前,基于Strom框架的聚类算法主要用于处理流式大数据的聚类问题,代表性工作总结如下:2014年,王铭坤等[114]设计了一个基于Storm框架的DBSCAN算法,使用集群搭载了1个nimbus节点和6个supervisor节点.实验结果显示,20 s大概能够吞吐2×106量级的数据.2016年,马可[115]在Storm框架下对经典流数据聚类算法CluStream[24]进行了并行实现,设计了分布式并行化实时流聚类算法DPRCluStream.实验结果显示,DPRCluStream算法的计算效率随数据量的增加呈近线性提升.2017年,李伟[116]通过引入微簇的簇密度和动态可调滑动的时间窗口,提出CluStream的改进算法S-CluStream,并在Storm框架下对S-CluStream进行了并行实现.2018年,王向阳[117]通过引入Kafka消息队列系统,构建了一个针对k-means聚类算法的Storm集群系统,用以处理海量微博数据的聚类问题.牛丽媛等[118]基于CluStream和DBSCAN算法,提出Stram框架下的分布式实时数据流密度聚类算法DBS-Stream.如何改善Storm框架下聚类算法实现效率的研究可参见文献[119].
3 讨论与展望
本文从大规模数据集的可计算性入手,分别对串行和并行计算环境下适用于大数据的聚类算法进行了阐释,以期为相关领域的研究提供借鉴.综上分析发现,基于集群的分布式计算已成为当前处理大数据聚类问题的主要手段,这正是对大数据实施“分而治之”策略的体现.尽管上述聚类算法表现出了一定的大数据处理能力,然而这些算法尚存在缺陷:① 过分注重聚类算法的并行;② 数据划分缺少统计支持;③ 需要人工干预,例如设定簇个数;④ 数据处理的实时性较差等.以下将给出一些关于未来处理大数据聚类问题的思考.
1)利用数据并行代替算法并行.尽管MapReduce和Spark计算框架表现出良好的大数据处理能力,但MapReduce处理迭代计算的性能较差,而Spark的内存计算又受到计算机内存容量的限制,因此,可以探索使用数据并行的策略来代替算法并行.一方面,聚类算法不需要并行化,能够降低算法训练过程中不同计算节点之间数据传输的频次;
另一方面,数据并行允许按照计算节点内存容量的大小划分原始的大数据集.为保证数据并行不产生有偏的聚类算法训练,可考虑在数据划分的过程中引入统计感知(statistical awareness)的概念,以期即保证数据子集与整体之间概率分布的一致性.本课题组在最新的研究中,在HDFS中引入随机样本划分(random sample partition, RSP)[120]的思想,从而保证了数据划分的一致性.图2形象地展示了随机样本划分对大数据划分的影响[117].其中,N为样本数量;B为窗口宽度.图2结果显示,在含有1×106个100维样本的大规模数据集(数据是约100 Gbyte)上,对于第1维特征,随机选取6个不同的数据块,HDFS数据块之间的概率分布差异非常大(图2(a)),而RSP数据块之间的概率分布则基本保持一致(图2(b)).
当得到大数据集的RSP数据块后,就可以在每个RSP数据块或多个RSP数据块的合并上(视计算节点的内存容量而定)训练单独的聚类算法,采用聚类集成(clustering ensemble)[121]的策略将不同RSP数据块上得到的聚类结果合并,从而得到大数据整体的聚类.此处的聚类集成应以统计原则为指导,以获得给定显著性水平下的等价聚类为准.
2)聚类算法训练的自动化. 最大限度地减少聚类过程中的人为干预是处理大数据聚类问题的关键之一.因为在大数据背景下,对于实际应用中产生的海量数据而言,很多情况下我们并不知道数据中到底蕴含了什么样的信息,这是与大数据4V(大量volune、高速velocity、多样varity和价值value)特性中的多样性和价值性对应.例如,在对电信用户行为数据进行用户分群的应用中,由于数据的体量巨大和实时更新,导致电信用户类型的个数无法预知.这就要求人们探索一种自动的、不依赖人为设定的簇个数确定机制.本课题组[122]在最新研究中,在k-means聚类算法的设计中引入了概率密度函数估计的思想,并提出了I-nice聚类算法.该算法能够自动识别数据集中包含簇的个数以及确定簇的中心.图3给出了简明图示来说明I-nice的聚类效果.从图3可见,与传统的k-means聚类算法(图3(a))相比,I-nice算法(图3(b))能够正确识别出数据集的簇中心.在未来的研究中,针对混合属性值数据的自动快速聚类算法研究将是大数据聚类领域的重要研究方向之一.
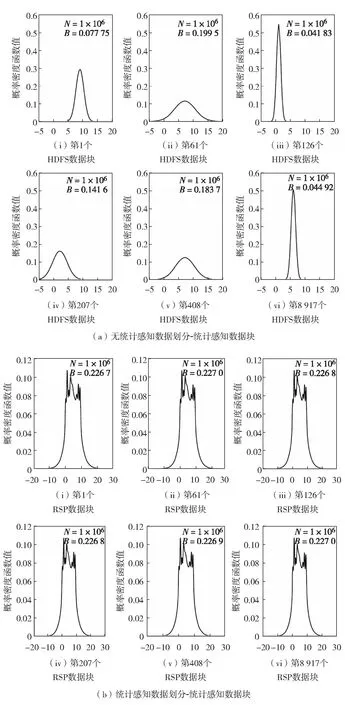
图2 数据块的概率分布[117]Fig.2 Probability distributions of data blocks[117]
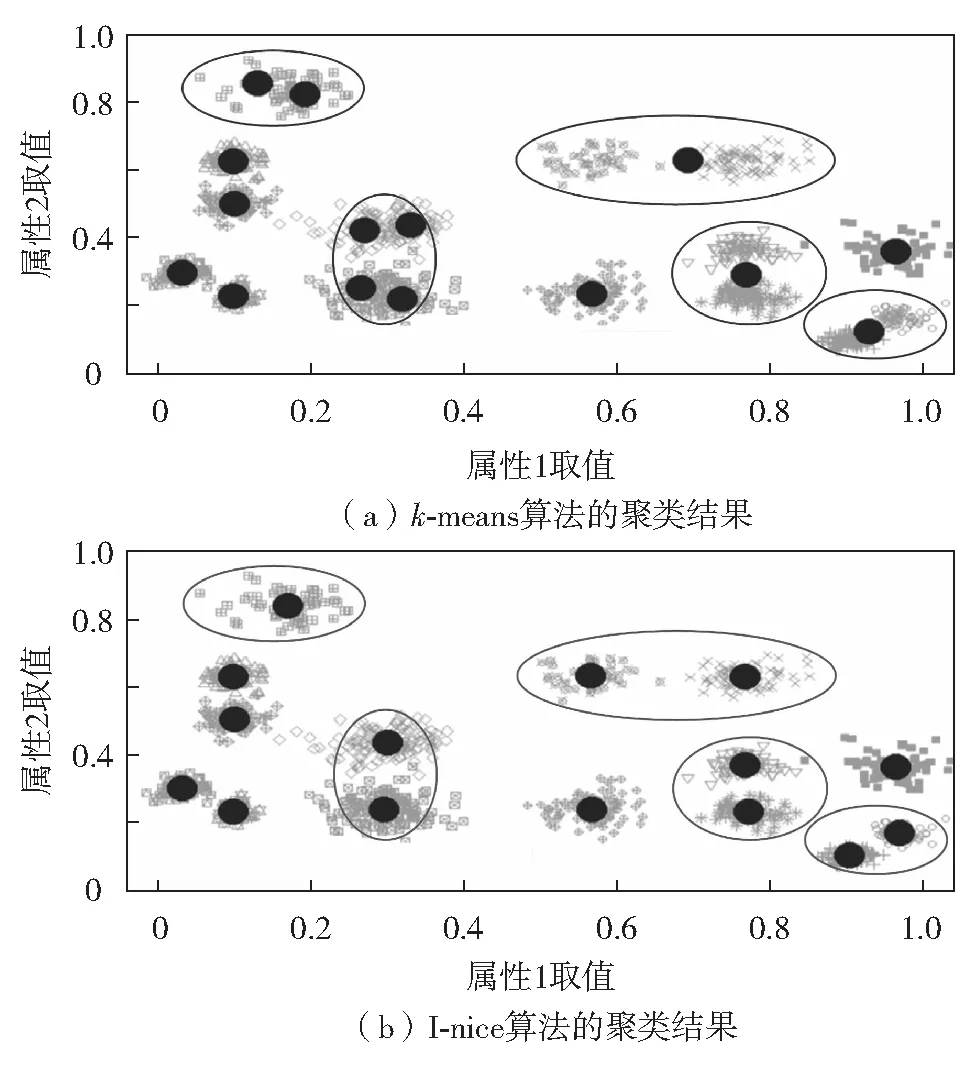
图3 自动聚类[119]Fig.3 Automatic clustering[119]
3)社交网络大数据的聚类.随着互联网技术的迅速发展和移动终端设备的广泛普及,社交网络(social network)[123]的价值日益突显.例如,2012年美国总统奥巴马的再次当选就是社交网络大数据改变美国总统竞选定律(谁花的钱多,赢得选举的概率就越大)的一个案例.社交网络是一种在互联网络上由社会个体的集合以及个体之间的连接关系构成的社会性结构,它具有体量巨大、复杂多变和形式丰富等特点.如何高效挖掘社交网络中蕴藏的巨大价值已成为目前大数据研究领域的热点.其中,对社交网络大数据进行聚类分析将是对社交网络展开价值挖掘的入口,它与社交网络中的网络社区结构、重叠社区发现和影响力最大化问题等直接相关.社交网络可以被抽样为一个图模型,基于大规模图数据开展的聚类分析,涉及图数据的划分以及基于子图聚类算法的融合两个重要问题:如何保证划分后的子图为整体图的随机样本是大图聚类分析的核心问题,即子图抽样的代表性问题;如何确保子图聚类结果的融合能够代表整体图上的聚类结果是大图聚类分析,即聚类集成的等价性问题.另外,大图聚类还要考虑到实时性的因素,聚类算法要能够根据数据的变化,快速地对已经获得的聚类结果进行改进和更新.
致谢:感谢西北工业大学聂飞平教授、北京交通大学景丽萍教授、山西大学曹付元教授、澳门科技大学韩迪博士以及深圳大学陈小军博士对本文的校验和建议!
