复杂屋盖结构表面风压的非高斯特性研究

夏俞超，陈水福

(浙江大学 建筑工程学院，杭州 310058)

大跨屋盖结构广泛应用于体育场馆、机场航站楼、购物中心等大型公共建筑中。由于这类结构具有跨度大、空间广、自重轻等特点，因而风荷载往往是其控制荷载。我国现行建筑结构荷载规范[1]仅给出了常见体型低矮房屋的屋面风荷载，而对于大跨屋盖结构一般建议通过风洞试验等方法获得其屋面的风荷载特性。目前国内外对平屋盖、马鞍形屋盖等常见体型大跨屋盖的表面风压已经有了较深入的研究，并获得了较多的共识：平屋盖表面风压以吸力为主，风吸力极大值一般出现在屋盖前缘，风压分布形式与风向角密切相关，风压系数受跨高比影响较小[2]；鞍型屋盖风压分布形式与平屋盖类似，所不同的是，风压系数受矢跨比影响较大[3]。但目前对复杂体型大跨屋盖，特别是开敞式复杂屋盖的研究还较为缺乏，从而影响了这类屋盖的抗风安全性。本文将从这类屋盖风压的概率分布特性出发开展一些探索。

早在1960年代，Davenport[4]就提出了风荷载符合高斯分布的基本设定，但Stathopoulos[5]通过对一系列低矮房屋的风洞试验发现，风压时程往往表现出明显的非高斯性质，他采用Weibull模型对其进行了较好的拟合。Holmes等[6-7]利用准定常和切片理论(Strip Theory)来估算风压的概率密度函数，结果显示在来流附着区的估算值与测量值较为一致，但在来流分离区该概率密度函数的拟合效果不理想，其主要原因是准定常理论对分离区并不适用。Letchford等[8]通过全尺寸实验验证了Holmes等的结论，并进一步发现面积平均风压与来流具有高度相关性。国内在近年也开展了针对足尺度房屋的风压分布研究，王旭等[9]对一坡角可调的试验房进行分析后发现，迎风区域和屋脊区域附近测点风压的非高斯特性较为明显。

Sadek等[10]采用概率图相关系数(Probability Plot Correlation Coefficient，PPCC)方法，利用指数分布、正态分布、对数正态分布、Gumbel分布、Weibull分布和Gamma分布等方法对低矮房屋风压时程的概率分布进行了拟合，得出三参数Gamma分布的拟合效果最佳。Tieleman等[11]进一步验证了这一结论，并给出了Gamma分布三参数的矩估计方法，克服了PPCC方法参数确定较复杂的缺点。但是以上研究考虑的均是风压时程偏度较小的情况。陈斌[12]针对典型低矮建筑，进行了风压概率分布与建筑几何参数的相互关系的研究，证明三参数的对数正态分布表征性较好，但也发现利用单一的概率分布函数拟合整个屋面上不同测点的风压比较困难。Cook[13]研究后认为，对同一风压概率分布，不同的概率密度函数在不同分段内的拟合效果并不一致，风压概率分布可以看成是几个概率密度函数的叠加。程红伟等[14]基于高斯混合模型，提出了非高斯密度函数表示方法，虽然该方法数学模型简单，但是混合模型的子分布仍为高斯分布，拟合效果有一定局限性。Huang[15]采用核密度法估计风压的概率分布，发现其对尾部概率分布的拟合效果不理想。陶玲等[16]基于PPCC方法，分别采用Gamma分布、广义极值分布和对数正态分布对测点风压系数时程进行了拟合比较，结果表明不同的概率分布函数适用于不同偏度的情况，当偏度达到1.5后，这三种分布的拟合效果均不理想。

本文以平坦海滩区域某开敞式复杂曲面形状的大跨屋盖结构为对象，在风洞试验的基础上，对屋盖在不同风向角下的平均和脉动风压的分布规律进行了分析；鉴于单一概率分布函数拟合效果不佳的特点，提出了采用三种概率分布组合模型：对数正态分布和Weibull分布组合(Lognormal-Weibull Mixture Distribution Model，LW)、双Weibull分布组合(Weibull-Weibull Mixture Distribution Model，WW)、双对数正态分布组合(Lognormal-Lognormal Mixture Distribution Model，LL)模型拟合风压时程样本的非高斯概率分布规律，并对各模型的准确性和适用性作了分析和比较。

1 工程概况与风洞试验

本文的研究对象是位于三亚某空旷海滩区域的一座商业中心主入口处的开敞式大跨复杂曲面屋盖结构，该商业中心的平面图如图1所示，主入口左右两侧连接着A楼、B楼，两楼之间前后通透，对来流风形成一定程度的狭道效应，故主入口处的风荷载预计较大，有必要对其进行风洞模型试验研究。

图1 商业中心平面图Fig.1 Plan of business center

该大跨屋盖结构采用网壳-桁架钢结构体系，两方向的跨度分别为113 m，73 m，屋盖最高处高度为39 m，结构形式见图2。这是一种单方向的开敞式结构，其主要特点是沿着入口处通道方向是开敞式的结构，而垂直于通道方向则与建筑物相连，有隔墙封闭。风洞模型试验根据设计单位提供的建筑设计图纸，按照几何相似要求，模型缩尺比为1∶150。风洞试验在浙江大学的ZD-1边界层风洞中进行(参见图3)。试验风速剖面采用我国现行荷载规范规定的A类地貌指数律公式，湍流度剖面按日本建筑规范中的湍流度剖面公式[17]。风洞试验的风向角定义及各分区典型测点布置示意图，如图4所示。

图2 主入口示意图Fig.2 Diagram of main entrance

图3 风洞中的缩尺试验模型Fig.3 Scale test model in wind tunnel

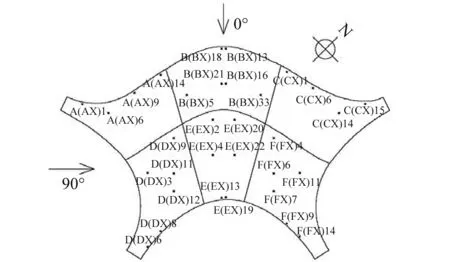
图4 风向角定义及分区典型测点示意图Fig.4 Diagram of wind direction angle and typical measuring points

2 风荷载特性

本次试验的采样频率为312.5 Hz，在24个风向角下均测得各测点10 000个时间步的风压系数时程。考虑到此屋盖为一开敞结构，故在上下表面均布置了风压测点，并将测得的上表面风压系数时程减去对应位置的下表面时程后，作为相应测点的净风压系数时程，如式(1)所示，再由式(2)、式(3)求得平均风压系数和脉动风压系数(即风压系数时程的标准差)

(1)

(2)

(3)

2.1 平均风压系数

本文主要讨论来流沿着开敞通道方向与垂直开敞通道方向这两个工况，研究结果可以为类似大型建筑入口处的单方向开敞式屋盖结构提供理论依据。0°，90°风向角下的平均风压系数等值线云图，分别如图5、图6所示。其中0°风向角下，来流沿着开敞通道方向，可以贯穿整个屋盖结构；90°风向角下，来流完全垂直于通道方向(沿着屋盖两侧连接的A楼、B楼的连线方向)。

图5 平均风压系数等值线云图(0°)Fig.5 Contour map of mean pressure coefficients (0°)

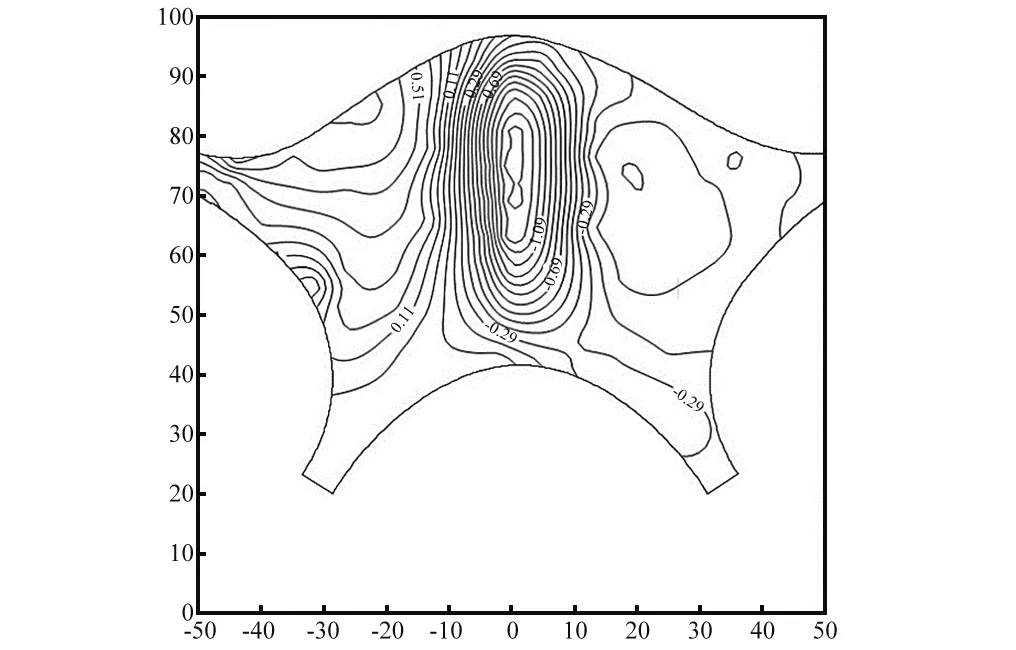
图6 平均风压系数等值线云图(90°)Fig.6 Contour map of mean pressure coefficients (90°)

由图5可见，在0°风向角下，屋盖的表面风压以负压为主，并且存在多处负压的极大值区；屋盖跨中范围依次排布了多个负压极大值区，这主要是由于屋盖复杂曲面造型所形成的来流多次分离与附着引起的；靠近屋盖前缘处的负压也较大，这与气流在前缘分离后形成的柱状涡有关。屋盖左右两侧也出现了绝对值较大的负压区，这与两侧A楼、B楼的存在相关。

在90°风向角下，屋盖迎风面表现为正压，最大正压出现在迎风侧外檐附近；靠近屋盖中部区域风压逐步减小并转化为负压，并在屋盖的跨中最高处由于分离剪切影响产生了最大负压；在屋盖的背风面，负压的绝对值又逐渐变小。

2.2 脉动风压系数

由于大气边界层近地面区域的湍流度较高，因此大跨屋盖结构表面会出现较明显的气流分离与再附着现象。图7和图8给出了0°和90°情况下的脉动风压系数等值线云图。可以看到，脉动风压系数分布与平均风压系数的分布情况有一定的相似性，尤其是屋盖中部区域的风压极值分布情况。实际工程中，一些大跨屋盖的围护结构因抗风性能不足而破坏，主要是由于脉动风压所产生的风致振动及疲劳效应所引起。

图7 脉动风压系数等值线云图(0°)Fig.7 Contour map of fluctuating pressure coefficients (0°)

图8 脉动风压系数等值线云图(90°)Fig.8 Contour map of fluctuating pressure coefficients (90°)

2.3 典型测点风压随风向角的变化

此结构沿着入口通道方向基本呈现轴对称的特点，C，F区域的风压分布分别与A，D区域的结果比较类似，因此只选取了A，B，D，E这四个区域中比较有代表性的几个测点A9，B18，D8和E2进行分析。这些测点的风压分布能够大致反映大跨屋盖不同区域的风荷载特性，其平均风压系数随风向角的变化曲线，如图9所示。可以看到，无论风向角如何改变，屋盖上的风荷载以吸力为主，风压系数主要分布在-1.1～0.7，较大的吸力主要分布在60°～90°与210°和270°风向角的屋盖前缘处和跨中凸起处。结构设计时应该针对局部风压特别大的区域采取适当的防范措施，防止该区域被风吸力所破坏。

图9 典型测点平均风压系数随风向角变化Fig.9 Mean wind pressure coefficients of typical measuring points vary with wind direction

图10为典型测点脉动风压系数随风向角的变化曲线。可以看到，随着风向角的变化，脉动风压系数介于0～0.5，最大的脉动风压系数出现在A9号测点的0°风向角下，这是由于此时的来流是正对主入口前缘，在前缘分离后形成的柱状涡所致。比较图9和图10的变化规律可见，平均风压系数与脉动系数之间不存在明显的相关性。

结合图9与图10可以看到，在255°风向角附近，典型测点的平均和脉动风压系数均达到极值，因此有必要对此风向角下的屋盖表面风压分布进行分析，特别是对量值较大的吸力的分析。图11和图12分别给出了255°风向角下的平均风压系数和脉动风压系数的等值线云图。由图可见，此风向角下屋盖表面的平均风压分布比较复杂，有多个负压极大值区，但主要分布在屋盖跨中屋脊线两侧，测点的最大平均风压系数达到-1.38。该风向角下的脉动风压分布也比较复杂，极值区同样分布在屋盖跨中屋脊附近，但分布范围更广一些，在设计中应作为重点区域加以关注。

图10 典型测点脉动风压系数随风向角变化Fig.10 Fluctuating wind pressure coefficients of typical measuring points vary with wind direction

图11 平均风压系数等值线云图(255°)Fig.11 Contour map of mean pressure coefficients (255°)

图12 脉动风压系数等值线云图(255°)Fig.12 Contour map of fluctuating pressure coefficients (255°)

从上述分析可以看到，与平屋盖类似，复杂屋盖表面的风荷载主要也表现为吸力，在迎风面的屋檐、屋盖的角区附近也出现了极大值。但所不同的是，这类复杂屋盖会在中部屋脊区域出现多个负压极大值区，这主要与复杂曲面所引起的气流多次分离与再附着有关。255°风向角下，吸力在屋盖跨中屋脊附近达到极大值。

2.4 非高斯特性

作用于屋盖表面的风压可以看作是分布在流场中的大量点涡相互叠加的结果。如果流场中每个点涡的作用是相互独立同分布的，其作用力之和的分布将趋于高斯分布。而复杂屋盖结构表面的风压往往呈现不对称分布的特点，即表现为非高斯分布。这主要是由于局部区域上的风压因来流在屋盖上分离再附着，产生了有组织、相关性较强的大尺度漩涡结构，点涡假设中每个点涡的作用是相互独立同分布已经不再成立，从而使得风压分布表现出非高斯特性。为了更准确地描述风压分布的非高斯特性，需要找到合适的数学表达工具，常采用偏度和峰度来表述其概率分布的偏离和凸起程度，当偏度为0，峰度为3时我们可以认为风压符合高斯分布[18]。但是，由于风的随机性以及可能存在的测量误差，高斯过程的偏度及峰度不适合取固定值，而应该是一个范围值。刘新等[19]研究后发现，以偏度绝对值是否大于0.5和峰度是否大于3.5作为区分高斯和非高斯过程的标准比较适合。测点风压系数时程的偏度和峰度分别按式(4)、式(5)计算

(4)

(5)

式中：Cpi,mean，Cpi,std分别为测点i风压系数时程的平均值和标准差。

利用上式计算了屋盖在不同风向角下所有测点的偏度和峰度，共计6 912个数据点，这些测点的偏度-峰度散点图如图13所示。经统计，有3 338个测点属于非高斯过程，而且可以看到小部分测点的峰度偏度远远偏离了高斯分布，用传统的高斯分布去拟合势必会造成很大误差。

图13 测点偏度-峰度散点图Fig.13 Scatter diagram of skewness and kurtosis

为了进一步研究典型测点在24个风向角下的偏度和峰度，图14和图15分别给出了测点偏度和峰度随风向角变化的折线图。可以看到，非高斯特性与风向角、测点位置密切相关。例如观察A9，B18测点在0°风向角的偏度和峰度，可以发现当测点处于来流区时非高斯特性不明显；而当测点处于气流分离区时，例如300°风向角下的A9测点、30°风向角下的D8测点，则表现出明显的非高斯特性。

图14 测点偏度随风向角的变化折线图Fig.14 Line chart of skewness of measured point vary with wind angle

图15 测点峰度随风向角的变化折线图Fig.15 Line chart of kurtosis of measured point vary with wind angle

3 风压概率分布

为了进一步分析屋盖风压的非高斯特性，下面对风压时程的概率分布作一研究。本文采用广泛应用的对数正态分布和Weibull分布作为子分布，并将其相互或自我组合形成三种概率分布混合模型，用于拟合屋盖非高斯风压时程样本的概率分布。根据陶玲的研究发现，偏度小的时程，对数正态分布拟合得较好；偏度大的时程，极值Ⅲ型(Weibull分布的一种形式)拟合得较好，因此这里采用这两种分布来组成概率分布的混合模型是合理的。

第一种混合模型为对数正态分布和Weibull分布组合(LW)，其概率密度表达式为

(6)

式中：k，c为Weibull分布概率密度函数参数；μ，σ为对数正态分布概率密度函数参数； 0<π<1。

第二种为双Weibull分布组合(WW)，其概率密度表达式为

(7)

式中：k1，c1，k2，c2分别为两个Weibull分布概率密度函数各参数，0<π<1。

第三种为双对数正态分布组合(LL)，其概率密度表达式为

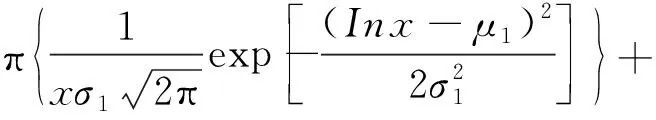
(8)

式中：μ1，σ1，μ2，σ2为两个对数正态分布概率密度函数各参数，0<π<1。

采用极大似然估计法来进行参数估计，从而得到三种混合模型的概率密度函数。为比较三者的适用性，图16给出了典型测点的风压系数频率分布直方图与三种混合模型对应的概率密度曲线，并与纯Weibull分布(W分布)作了比较。从图中看到，三种概率分布混合模型对风压系数概率分布的拟合程度有一定的差别，但拟合效果均好于单Weibull分布。相比之下，0°风向角下A09测点的情况较为复杂，其风压概率密度呈现出双峰分布的情况，此时Weibull分布拟合出的曲线仍呈现单峰形式，导致拟合效果不佳，而LW混合模型则仍然表现出了良好的拟合效果。

图16 典型测点风压系数概率分布直方图Fig.16 Probability distribution histogram of wind pressure coefficients

为了评价风压概率分布混合模型的拟合效果，采用RMSE方法[20]来进行定量分析。RMSE值的计算式如式(9)所示，其值越小，表示被检验的概率分布模型的拟合度高。

(9)

式中：Fic，Fi分别为i点的目标积累概率分布值和被检验累积概率分布值。

表1给出了代表性测点风压概率分布混合模型的误差评价。由表可见，对于典型测点的风压概率分布，三种混合模型的吻合程度有一定差别，其中对于大部分测点来说，LW混合模型最为符合。

表2给出了代表性测点的偏度、峰度值。可以看到，前面所选取的测点及相应风向角的情况主要是偏度较小(小于0.8)的情况，以下专门对偏度较大(大于0.8)的情况作一分析。据此选取A6，C14，F9，F14分别在0°，270°，165°，225°风向角下的风压时程数据进行拟合，其概率分布密度直方图如图17所示。

表1 代表性测点风压概率分布混合模型误差评价Tab.1 Error evaluation of probability distribution of typical measuring points

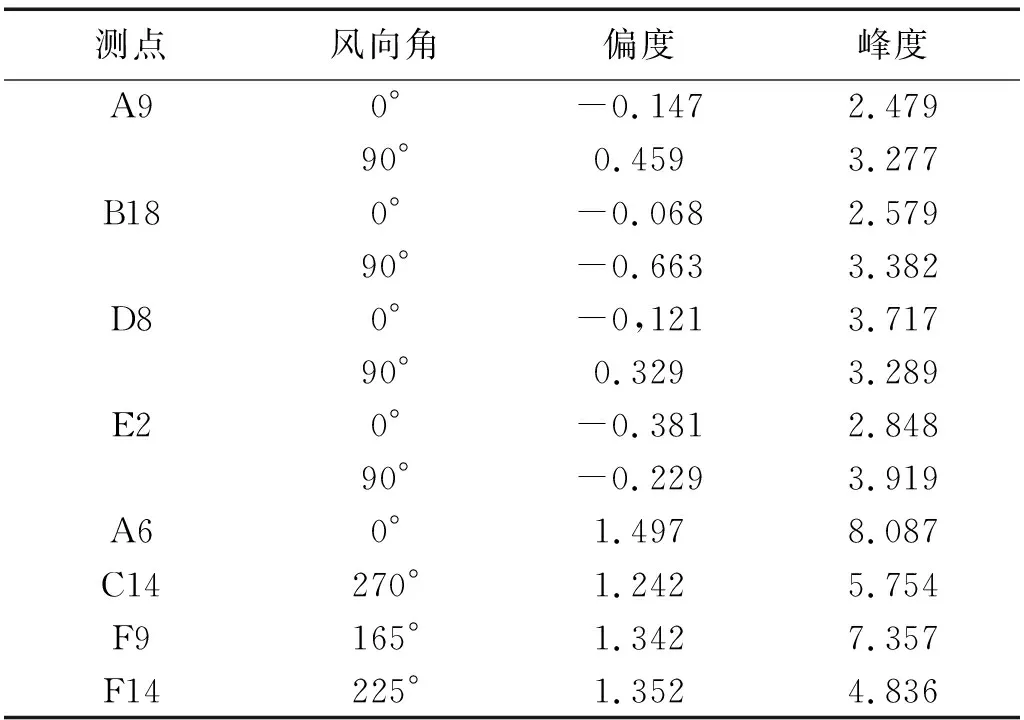
表2 测点偏度、峰度Tab.2 Skewness and kurtosis of measuring points

类似地，我们同样采用RMSE方法进行误差评价，表3给出了这些测点风压概率分布混合模型的误差评价值。可以看到，LW混合模型的拟合效果要优于其他两种混合模型。由此可见，对于偏度较大(大于0.8)的情况，LW混合模型同样表现出了良好的拟合效果。其主要原因是LW混合模型集合了对数正态分布和Weibull分布的优点，因而组合而成的混合模型对不同偏度的情况均有良好的适用性。研究中讨论了不同部位的代表性测点在不同风向角下的效果，LW混合模型均表现出了良好的拟合效果，可以认为对于此类的复杂屋盖结构的适用性较好。在实际应用中，推荐采用LW混合模型进行此类大型建筑入口处的开敞式复杂屋盖结构的风压概率密度分布的拟合。但是限于篇幅的关系，并未对其他结构形式的大跨屋盖进行拟合与分析，此混合模型是否具有普适性需要后续研究。

图17 偏度较大测点风压系数概率分布直方图Fig.17 Probability distribution histogram of wind pressure coefficients with large skewness表3 偏度较大测点风压概率分布混合模型误差评价Tab.3 Error evaluation of probability distribution of measuring points with large skewness

测点风向角概率分布混合模型LWWWLLA60°0.004 490.010 70.005 42C14270°0.003 920.006 230.010 6F9165°0.008 570.009 810.012 4F14225°0.004 240.007 410.004 53

4 结 论

以沿海某复杂曲面形状的大跨屋盖结构为研究对象，通过风洞模型同步测压试验，对其表面风压分布特性进行了研究，提出并运用三种概率分布混合模型对屋盖的非高斯风压分布规律进行了拟合和计算分析，据此可得出以下结论：

(1) 与平屋盖及简单曲面屋盖类似，复杂体型屋盖结构的表面风压主要也表现为吸力作用，吸力极大值一般出现在迎风面的屋檐、屋盖的角区；所不同的是，这类复杂屋盖还会在跨中区域出现多个吸力极值区，这主要与复杂曲面所引起的气流多次分离与再附着有关。

(2) 讨论了来流沿着开敞通道方向与垂直开敞通道方向这两个工况下屋盖表面的风压分布，研究结果适用于类似的大型建筑入口处的单方向开敞式屋盖结构，可以为同类结构的风荷载确定提供依据。同时发现在255°风向角附近，吸力在屋盖跨中屋脊附近达到极大值，在今后的设计中应该重点关注斜风向对大跨屋盖结构的破坏。

(3) 复杂屋盖结构表面的相当一部分测点都表现出了非高斯特性。研究表明当测点处于来流区时非高斯特性不明显，而当测点处于气流分离区时则表现出明显的非高斯特性。

(4) 三种概率分布混合模型对该复杂屋盖风压系数的概率分布均表现出了较好程度的拟合效果，相比而言，LW混合模型最为符合风洞实测风压时程的概率分布，该模型对不同偏度的风压分布情况均有良好的适应性，可以用来描述此类大型建筑入口处的开敞式复杂屋盖结构表面的风压分布，但是对于其他形式的大跨结构，该模型是否具有普遍性仍需后续研究。