一种六自由度准零刚度隔振平台
2019-01-23肖庆雨周加喜徐道临
肖庆雨, 周加喜, 徐道临, 2, 王 凯
(1.湖南大学 机械与运载工程学院,长沙 410082; 2.汽车车身先进设计制造国家重点实验室,长沙 410082)
随着隔振技术在高精密工程领域的广泛应用,以及对低频隔振性能的要求越来越高,新的低频或超低频隔振方法成为研究难点和热点。传统的线性隔振技术对于低频振动,往往无法平衡系统稳定性与隔振效果间的矛盾。准零刚度隔振方法是一种非线性隔振方法,其利用正负刚度元件并联组合获得高静刚度和低动刚度,可同时降低隔振系统的静位移和自振频率,从而实现低频甚至超低频隔振。
近年来,诸多学者对准零刚度隔振技术展开了深入的研究,有力地推动了准零刚度隔振技术的发展。Alabuzhev等[1]首次较为全面地对准零刚度隔振系统的理论进行了阐述,并提出了若干设计方法。Carrella等[2]利用3根弹簧组合给出了准零刚度隔振器的分析模型,研究了其静力学特性及隔振性能。徐道临等[3]通过实验验证了此类准零刚度隔振器的低频隔振性能。Kovacic等[4]利用预压非线性弹簧替代线性弹簧,解决了系统动刚度在偏离平衡位置后急剧变化的问题。Zhou等[5]用磁力弹簧替代机械弹簧来获得高静刚度低动刚度性能,从而实现低频隔振。Huang等[6]开展了冲击激励下基于欧拉梁负刚度结构的隔振系统的理论与实验研究。Shan等[7]将两个相排斥的磁环与气动弹簧组合,设计了具有高静低动特性的小型气动隔振装置。Zheng等[8]将互斥磁环与弹簧组合设计了一种高静低动刚度隔振器。Hao等[9]分析了典型准零刚度隔振系统的隔振特性。王毅等[10]针对重载低频隔振难题,设计了一种紧凑的滚球型准零刚度隔振器。
然而,现有的准零刚度隔振方法大多关注单向隔振,关于六自由度准零刚度隔振的研究还比较少见。Sun等[11]利用四个类剪铰装置对称组合实现了其在三个平动方向上的准零刚度特性。Platus[12]利用屈曲欧拉梁与螺旋弹簧构造了一种六自由度低频隔振系统。Wu等[13]将剪铰装置作为Stewart平台的支撑,设计了一种六自由度准零刚度隔振平台。
本文基于凸轮-滚珠-簧片梁负刚度机构设计了一种紧凑的准零刚度压杆,并将其应用于八杆隔振平台[14],提出一种新型的六自由度准零刚度隔振平台,并对其静力学和动力学特性进行分析,评估其隔振性能。通过与相应的线性平台进行对比,验证其优异的低频隔振性能。
1 准零刚度压杆
如图1所示的准零刚度压杆,主要由具有负刚度的凸轮-滚珠-簧片梁机构和正刚度元件轴向弹簧并联组成。1-球铰;2-细长内杆;3-直线轴承;4-5-6-圆柱外套筒;7-可调节式圆柱内套筒;8-轴向弹簧;9-半开口式圆柱套筒;10-环形套;11-簧片梁;12-万向滚珠;13-螺栓;14-半球环形凸轮。当压杆在平衡位置附近振动时,凸轮偏离静平衡位置,带有滚珠的簧片梁在轴向产生负刚度,从而减小整个系统的轴向刚度,当产生的负刚度与轴向弹簧的正刚度相等时,平衡位置的刚度为零,由此可推出压杆的零刚度参数条件。

(a)
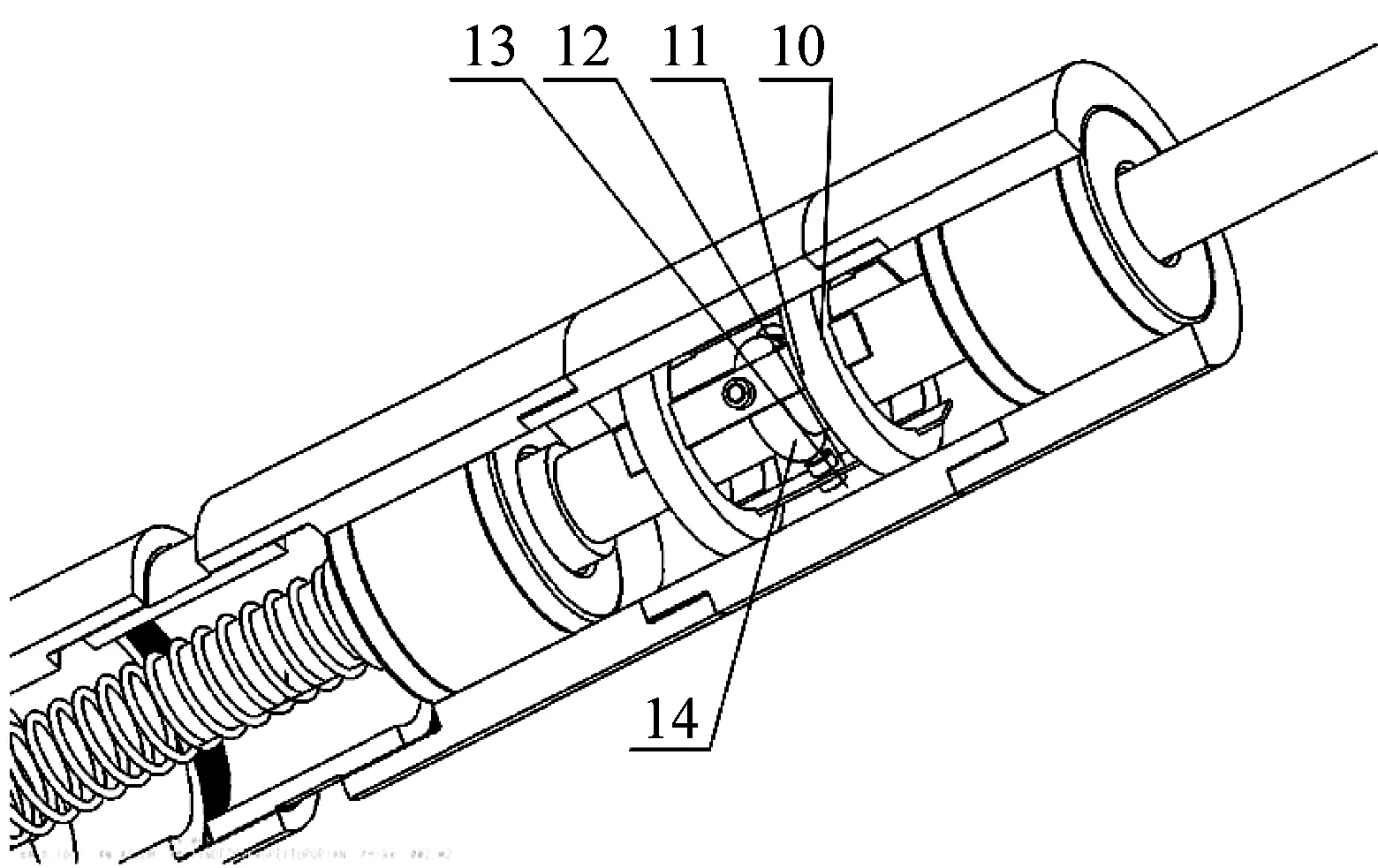
(b)
准零刚度压杆的静力分析图如图2所示。静载P作用下,压杆处于静平衡位置,即凸轮圆心与滚珠圆心在同一水平线上,其受力分析如图2(a)。此时,轴向弹簧的预压量为Δx=P/kv,其中kv为轴向弹簧的刚度。当压杆在外载f(x)作用下,凸轮偏离静平衡位置向下移动x,此时压杆受力分析如图2(b)所示,细长内杆与簧片梁各自的受力分析可见图2(c)。通过静力学分析,可得外载f(x)对x的关系表达式
(1)
式中,EI为簧片梁的弯曲刚度,L为簧片梁的跨距长度,r1和r2分别是万向滚珠和半球环形凸轮的半径,δ为簧片梁未发生形变时半球环形凸轮和万向滚珠两圆心之间的距离。

(a)(b)

(c)
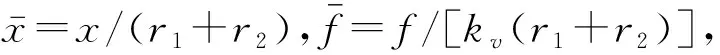
(2)
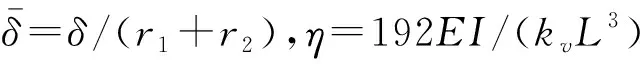
(3)

(4)
将零刚度参数条件分别代入式(2)和(3),可得准零刚度压杆的无量纲回复力和刚度
(5)
(6)


图3 准零刚度压杆在不同值下的无量纲刚度曲线
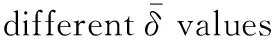
为便于后续准零刚度隔振平台的力学分析,将式在平衡位置处进行泰勒展开,并近似表示为
(7)

2 六自由度准零刚度隔振平台
为解决多向低频隔振的难题,基于八根准零刚度压杆组合设计了一种新型六自由度准零刚度隔振平台,如图4所示。其中,1-被隔振质量,2-支撑平台,3-准零刚度压杆,4-基础平台。八根准零压杆两两组合且关于平台中心轴(z轴)对称布置,且每根压杆与中心轴间的夹角均为φ,其中各压杆投影后与坐标轴x或y之间的夹角记为β。由压杆连接的支撑平台及固定其上的负载(被隔振设备)可以沿六个自由度平动和转动,而基础平台则用于隔振平台的支撑与固定。较六压杆平台,八压杆平台稳定性与承载能力更强。

(a)

(b)
2.1 静力学特性分析
考虑在准零刚度隔振平台上支撑平台中心同时施加外载荷(Fx,Fy,Fz,Mx,My,Mz)T,设支撑平台中心产生位移为(x,y,z,θx,θy,θz)T,则支撑平台上四铰点A、B、C、D的位移量为
ΔxA=x,ΔyA=y+rθz,ΔzA=z-rθy
ΔxB=x-rθz,ΔyB=y,ΔzB=z+rθx
ΔxC=x,ΔyC=y-rθz,ΔzC=z+rθy
ΔxD=x+rθz,ΔyD=y,ΔzD=z-rθx
(8)
根据准零刚度隔振平台各铰点上的位移量,可计算出平台中各压杆的轴向变形量,鉴于压杆变形量相对压杆杆长小得多,可近似表示为
Δl1=-xsinφcosβ+ysinφsinβ+zcosφ-
θyrcosφ+θzrsinφsinβ
Δl2=-xsinφcosβ-ysinφsinβ+zcosφ-
θyrcosφ-θzrsinφsinβ
Δl3=-xsinφsinβ-ysinφcosβ+zcosφ+
θxrcosφ+θzrsinφsinβ
Δl4=xsinφsinβ-ysinφcosβ+zcosφ+
θxrcosφ-θzrsinφsinβ
Δl5=xsinφcosβ-ysinφsinβ+zcosφ+
θyrcosφ+θzrsinφsinβ
Δl6=xsinφcosβ+ysinφsinβ+zcosφ+
θyrcosφ-θzrsinφsinβ
Δl7=xsinφsinβ+ysinφcosβ+zcosφ-
θxrcosφ+θzrsinφsinβ
Δl8=-xsinφsinβ+ysinφcosβ+zcosφ-
θxrcosφ-θzrsinφsinβ
(9)
本文仅考虑微幅振动,即平台各压杆中的凸轮与滚珠始终保持接触,则压杆内力表达式可写成
(10)
式中,γ=kvγ/(r1+r2)2。对准零隔振平台进行静力学分析可得
Fx=4γa[a3(c4+s4)x3+6a3c2s2xy2+3ab2(c2+s2)xz2-
6a2bc2srθxxy+3a2bs3rθyx2+3a2bc2srθyy2+
(11)
Fy=4γa[a3(c4+s4)y3+6a3c2s2x2y+3ab2(c2+s2)yz2+
6a2bc2srθyxy-3a2bc2srθxx2-3a2bs3rθxy2-
(12)
Fz=4γb2[2b2z3+3a2(c2+s2)x2z+3a2(c2+s2)y2z-
6absrθxyz+6absrθyxz-6a2c2r2θxθzx-
(13)
Mx=-4γbr(a3s3y3+3a3c2sx2y+3ab2syz2-
3a2bc2rθxx2-3a2bs2rθxy2-3b3rθxz2+
(14)
My=4γbr(a3s3x3+3a3c2sxy2+3ab2sxz2+3a2bs2rθyx2+
3a2bc2rθyy2+3b3rθyz2-6a2bc2rθzyz+
(15)
Mz=4γa2c2r2[3a2(c2+s2)θzx2+3a2(c2+s2)θzy2+
6b2θzz2-6b2θxxz-6b2θyyz-
(16)
式中,a=sinφ,b=cosφ,c=sinβ,s=cosβ。
2.2 动力学特性分析
考虑在准零刚度隔振平台六个方向上同时施加简谐激励,并考虑阻尼影响,引入线性黏性阻尼,令系数为ci,i=1~6,其动力学方程可表示为

(17)
式中,
u={x,y,z,θx,θy,θz}T
M=diag[m,m,m,Ix,Iy,Iy],K=0
C=diag[c1,c2,c3,c4,c5,c6],F=Ft-FR
Ft={Fxo,Fyo,Fzo,Mxo,Myo,Mzo}Tcoswot
FR={Fx,Fy,Fz,Mx,My,Mz}T
(18)
引入无量纲项
(19)
故准零隔振平台的动力学方程可写为下面的无量纲形式

(20)
其中
ζ=diag{ζ1,ζ2,ζ3,ζ4,ζ5,ζ6},
(21)
3 数值仿真与讨论
准零刚度隔振平台的无量纲参数如下所示

(22)
其中,准零刚度隔振平台平动自由度上的激励力幅值均取为被隔振重量的1/10。
3.1 隔振平台的刚度

平面

平面

平面

平面


平面

平面

平面

(d) θyθx平面
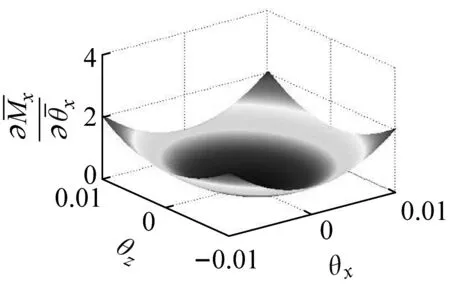
(e) θzθx
3.2 力传递率
一般利用力传递率评估系统的隔振性能,其定义为传递到基础的力的幅值与激振力的幅值的比值。但鉴于准零刚度系统响应的复杂性,通常用传递力和激励力时间历程的均方根的比值来定义力传递率,即:
(23)

利用龙格-库塔方法求解隔振平台的动力学方程得到稳态响应的时间历程,进而计算力传递率。通过向后扫频分析,可得传递率随激励频率变化的曲线,如图所示。为体现准零刚度平台隔振性能的优越性,将其与线性隔振平台进行对比。图中实线和虚线分别为准零刚度和线性隔振平台在各自由度上的力传递率曲线。其中,线性隔振平台是指由八根撤除了负刚度机构仅由轴向弹簧支撑的压杆组合而成的平台。
由图7可知,准零刚度隔振平台在各自由度上的力传递率峰值均低于线性隔振平台,且准零刚度隔振平台的下跳频率均未超过线性隔振平台的固有频率。当激励频率超过下跳频率后,准零刚度平台开始发挥隔振作用,其力传递率远小于线性隔振平台,尤其在线性平台共振区域附近;准零刚度隔振平台的有效隔振区域明显宽于线性隔振平台,且隔振效果显著提升。由此可见,准零刚度隔振平台的隔振性能明显优于相应的线性隔振平台。相应线性系统平动x与转动θy,平动y与转动θx存在弹性耦合,因此两个平动(x,y)和两个转动(θx,θy)四个自由度上的力学传递率出现两个峰值。注意θy自由度上的力传递率TMy在Ω稍大于0.5处有一个很小的峰值,与x自由度上的力传递率TFx的第一个峰值相对应。

(a) TFx

(b) TMx

(c) TFy

(d) TMy

(e) TFz

(f) TMz
3.3 倾角φ对平台隔振性能的影响
结合准零刚度隔振平台载荷-位移关系式(11)~(16)发现,倾角φ对平台刚度及承载能力影响较大。图8和图9描述了倾角φ对准零刚度隔振平台隔振性能的影响。从图8可以看出,随着倾角φ的变化,准零刚度平台不同自由度上的力传递率曲线在下跳频率前所受影响不尽相同。在所选三组倾角φ值中,倾角φ的越大,x,y平动方向和z转动方向上的力传递率峰值越大,而x,y转动方向和z平动方向上的传递率峰值越小。由图8可知,随倾角φ的增大,下跳频率在x,y平动方向和z转动方向上先急剧增大再缓慢减小,而在x,y转动方向和z平动方向上则是先缓慢减小再急剧减小。下跳频率越小,准零刚度隔振平台的起始隔振频率越低,其隔振频带越宽,低频隔振效果越好。鉴于此,倾角φ越大,平台隔振性能越好。但增大倾角φ会减弱平台承载能力。因此,为提升平台的隔振性能,应根据实际承载情况设计合理的倾角φ。

(a) TFx

(b) TMx

(c) TFy

(d) TMy

(e) TFz

(f) TMz

(a) Ωdx
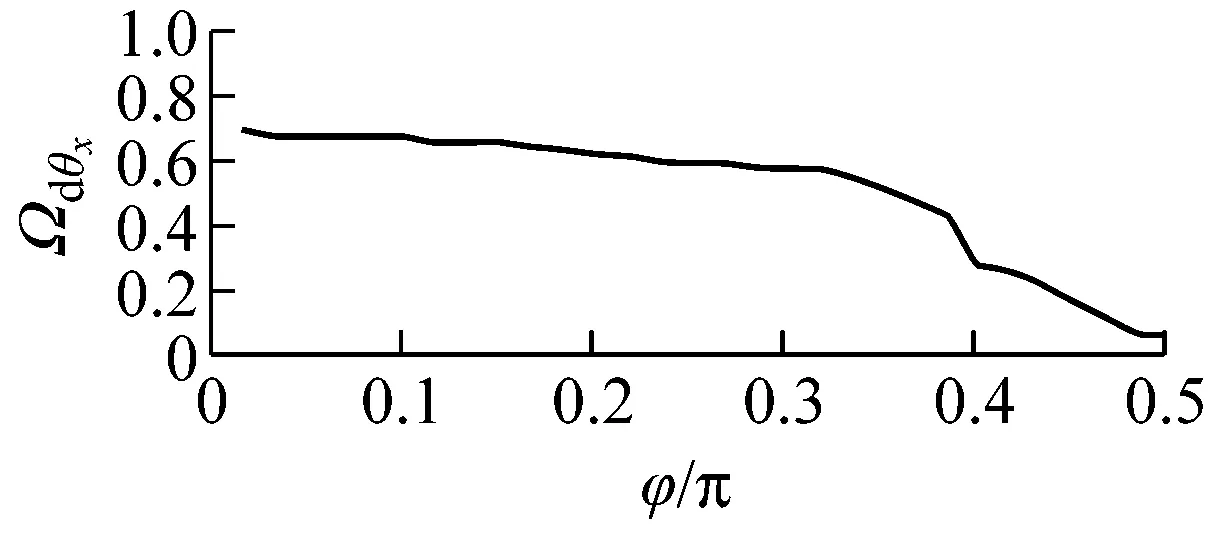
(b) Ωdθx

(c) Ωdy
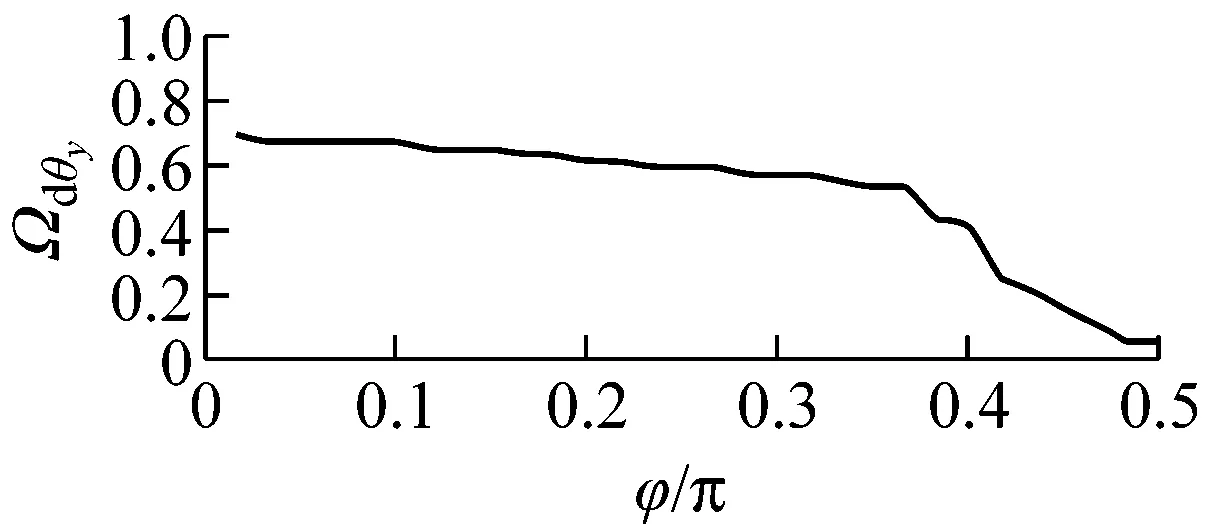
(d) Ωdθy

(e) Ωdz

(f) Ωdθz
4 结 论
针对多向低频隔振,本文设计了一种含凸轮-滚珠-簧片梁负刚度机构的准零刚度压杆,通过静力分析推导了静平衡位置处的零刚度参数条件;基于该准零刚度压杆,提出了一种八压杆准零刚度隔振平台,并对其静、动力学特性及隔振性能进行了分析。得出以下结论:
(1) 准零刚度隔振平台在各自由度上的隔振性能均优于相应的线性隔振平台,起始隔振频率和低频区域内的传递率均显著低于线性隔振平台,实现了六自由度低频隔振。
(2) 压杆倾角φ对准零隔振平台的隔振性能有较大影响,合理设计倾角φ可同时保证承载能力和提高隔振性能。
