频率相关黏性阻尼理论的时程积分计算

2019-01-23孙攀旭刘庆林

振动与冲击 2019年1期

孙攀旭，杨红,2，刘庆林

(1.重庆大学土木工程学院，重庆 400045；2.重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045；3.深圳信息职业技术学院交通与环境学院，深圳 518172)

黏性阻尼理论时程计算具有稳定收敛的优点，但存在能量耗散与外激励频率相关的缺点[1]；复阻尼理论的每周期消耗能量与外激励频率无关，但方程通解中含有发散项，导致时程计算不稳定[2]。克服黏性阻尼理论和复阻尼理论的缺陷，寻求一种新阻尼理论对有助于改善结构动力时程响应计算的合理性和适用性。

复阻尼运动方程计算求解时，需要依据对偶原则得到复化对偶项[3-5]，同时为保证结构动力响应计算的稳定收敛，直接剔除发散项的做法在数学处理上是不合理的[6]。因此复阻尼运动方程本质是频域运动方程，不能直接推广到时域中进行计算[7-8]。朱镜清[9]将外激励频率考虑到黏性阻尼理论的阻尼力项中，得到频率相关黏性阻尼运动方程，其为谐波作用下复阻尼运动方程在实数域中的表达，但无法直接适用于自由振动反应中。本文依据频域转化原则，提出包含结构振动频率参数的频率相关黏性阻尼运动方程，在满足时程计算稳定收敛的同时，保证了每周期能量耗散与外激励频率无关。为方便方程的时程计算，基于速度与位移关系假定和能量守恒准则，进一步构建了适用于时程计算的运动方程，结合常平均加速度法、Newmark-β法等，可得到时程积分计算的递推表达式，实现了频率相关黏性阻尼理论的时程积分计算。

1 基于频率相关黏性阻尼的时域积分

1.1 基于复阻尼的频率相关黏性阻尼

单自由度体系的复阻尼运动方程为

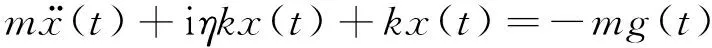
(1)

式中，m为结构质量，k为结构刚度，η为复阻尼系数，g(t)为地震加速度，i为虚数单位。

复阻尼运动方程的通解中包含有发散项，发散项为指数增长函数形式，而指数增长函数在区间[0,+∞)上不可积分，其傅里叶变换不存在，将式(1)转换到频域的过程实质上是一个过滤发散项的过程，因此频域运动方程是稳定的。将式(1)进行傅里叶变换，可得

(2)

当结构位移响应的振动频率不为零时，式(2)可转化为

(3)

经傅里叶变换之后，得时域运动微分方程为

(4)

式(4)对应的特征方程为

(5)

式(5)的特征根为

(6)

式(4)对应的齐次方程通解为

xc(t)=[Acos(βt)+Bsin(βt)]e-αt

(7)

其中，

(8)

设单自由度系统在激励频率为θ的谐波作用下，结构的振动频率与谐波激励频率相同，位移响应为x=X1sin(θt)+X2cos(θt)，频率相关黏性阻尼理论中其阻尼力项为

(9)

一个振动周期内阻尼力做的功为

(10)

阻尼力做功与消耗的能量相等，由式(10)可知在简谐荷载作用下频率相关黏性阻尼理论中阻尼每一周期消耗的能量与外激励频率无关。

频率相关黏性阻尼与复阻尼在频域范围内是等价的，具有每个周期消耗能量与外荷载激励频率无关的优点，同时频率相关黏性阻尼运动方程通解中不包含发散项，时程积分计算稳定收敛。

1.2 基于速度与位移关系的频率相关黏性阻尼

频率相关黏性阻尼运动方程中含有结构振动频率，结构振动频率为未知项，因此式(4)无法直接采用逐步时程积分计算。假定结构位移响应的振动频率为速度与位移的比值绝对值[10]，即

(11)

将式(11)代入式(4)，可得

(12)

由式(12)可知，此时阻尼力是与弹性力大小成正比，且与运动速度反向，该规律与朱镜清和Chen等[11]的研究成果一致，阻尼力为

(13)

设单自由度系统响应x=Xsin(θt)，一个振动周期内阻尼力做的功为

ΔW=-2ηkX2

(14)

结构的损耗因子为

(15)

由式(14)和(15)，可得到结构阻尼一个周期内消耗的能量为[12]

ΔE=πηkX2

(16)

此时，一个周期内消耗的能量与阻尼做功大小并不相等，依据结构阻尼消耗的能量对运动方程进行修正，改进阻尼力为

(17)

单自由度系统响应x=Xsin(θt)，一个振动周期内阻尼力做的功为

ΔW=-2λkX2

(18)

简谐激励作用下结构内部阻尼在一个振动周期内消耗的能量ΔE与等效阻尼力在一个周期内消耗的能量ΔW相等，且η=2ξ，故比例系数λ为

λ=πξ

(19)

由此可得到新的运动方程为

(20)

(21)

其中，

(22)

采用数值积分方法进行计算时，按照时间步长Δt进行离散，任意时刻可表示为tk=kΔt(k=0,1,2…)，利用tk时刻结构的动力响应，计算tk+1时刻结构的动力响应，但tk+1时刻的τ值无法确定，进而无法得到运动方程。当时间步长取值足够小时，可利用tk时刻结构的动力响应确定tk+1时刻的τ值，并得到tk+1时刻的运动方程，由此进行迭代计算。

采用常平均加速度法，tk+1时刻结构的速度和位移为[13]

(23)

将式(23)代入式(21)可得

(24)

其中，

δ=πξτkk+k

(25)

(26)

由式(23)～(26)即可实现基于平均加速度法的频率相关黏性阻尼时域积分计算。

多自由度体系的频率相关黏性阻尼运动方程为

(27)

式中，g(t)为地震加速度，I为与地震动输入有关的向量(N×1)，与g(t)方向相同的位移自由度元素为1，Ω为符号矩阵。

(28)

(29)

将单自由体系的基于平均加速度法的频率相关黏性阻尼时程计算方法应用到多自由度体系，即可完成时程积分计算。

2 算例分析

如图1所示，以钢-混凝土组成的5层剪切型混合框架结构为例，钢结构的阻尼比为0.02，钢筋混凝土结构的阻尼比为0.05[14]。

图1 竖向混合框架结构的质量和刚度分布

Fig.1 The mass and stiffness distribution of vertical mixed structure frame

质量矩阵为

(30)

刚度矩阵为

K=105N/m×

(31)

复阻尼理论下阻尼矩阵为

C=105N/m×

(32)

如图2(a)、图2(b)所示，当地震作用持续时间分别小于15 s、9 s时，频率相关黏性阻尼理论时程计算结果与复阻尼理论时程计算结果一致，证明本文提出的频率相关黏性阻尼时程计算方法的正确性。在图2中，随着地震作用持时增加，复阻尼理论计算的结构顶层位移逐渐发散，因此复阻尼理论只能合理地计算地震持时较小时的结构位移响应，持时较大时计算结果将会发散。相对于复阻尼理论的时程计算结果，频率相关黏性阻尼的计算结果在地震持时较大时依然保持了稳定收敛。

(a) 迁安波东西方向分量

(b) El Centro波东西方向分量

Fig.2 Calculated results of structural top displacements with different methods

以结构顶层最大位移为指标，对混合结构的阻尼比进行敏感性分析。如图3所示，钢筋混凝土结构的阻尼比保持0.05不变，通过改变钢结构的阻尼比，计算出对应的迁安波东西分量作用下结构顶层最大位移变化率(GJ)；钢结构的阻尼比保持0.02不变，通过改变钢筋混凝土结构的阻尼比，计算出对应的迁安波东西分量作用下结构顶层最大位移变化率(GJH)。由图3可知，相比结构阻尼比的减小，阻尼比的增大对结构顶层最大位移变化的影响更大；相比钢结构阻尼比，钢筋混凝土结构阻尼比对结构顶层最大位移变化的影响更大。