基于弯曲模态的板形直线超声电机结构设计

张百亮， 姚志远， 简 月， 李晓牛

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

直线超声电机是一种新型作动器，利用压电材料的逆压电效应将电能转换为定子机械振动能，再通过摩擦作用将定子的机械振动能转换为动子的动能。它具有结构简单、直接驱动负载、断电自锁、低噪声、无电磁干扰和定位精度高等特点，已被广泛应用于航空航天、武器装备和精密仪器等领域[1-2]。近年来直线超声电机的研究受到关注，多种满足特定使用要求的新构型直线超声电机[3-12]陆续提出和开发，以满足不同场合对作动器的需求[13]。例如，物理光栅三维扫描仪需要在29 mm×23 mm×3 mm狭小空间内调整光栅位置[14]；缓冲气囊在着陆缓冲过程需要体积小、执行力大、响应快的作动器实时控制气囊排气口大小[15]；引信安全系统中需要扁平结构的作动器驱动引信隔爆机构运动，且要求作动器无电磁干扰[16]。板形直线超声电机因具有扁平化结构、空间利用率高和易微型化设计等特点[17]，特别适用于上述安装空间狭窄且需要一定推力的直线驱动场合，因而板形直线超声电机有着良好的应用前景。

在结构形式上，板形直线超声电机最简单的定子形式为矩形结构。Tomikawa等[18]设计了一种贴片式的矩形板结构直线超声电机，它利用矩形板同频的纵向振动和弯曲振动，在驱动足处形成椭圆运动，驱动动子运动。该电机具有结构简单和运行效率高的优点，更利于设计。此后，类似矩形板结构电机[19-21]被相继提出，它们多采用矩形板纵、弯振耦合模态和贴片式结构。然而，在一个结构上同时配置纵振陶瓷片和弯振陶瓷片激发两相振动，一定程度上增加了结构设计的复杂性；贴片式结构利用压电陶瓷的d31模式，定子能量转换效率较低，推力小。此外设计的定子要求两相工作模态频率接近，无疑增加了结构设计难度，降低了电机设计的灵活性。采用单模态驱动是解决模态频率一致性问题的一种途径[22]。Liu等[23]提出了一种单模态驱动的直线压电电机。该电机定子为一板结构压电振子，分别采用纵振和弯振的激励方式激发板的两相振动模态，通过切换两相模态实现电机双向运动。实验表明定子两相模态驱动电机的性能存在差异，且在弯振激励的模态下，电机具有更大的输出力和更高的能量转换效率。

在满足狭窄空间、大推力作动需求的应用背景下，为克服模态耦合型超声电机的频率一致性调节要求的限制，本文提出了一种单模态、大推力直线超声电机。该电机利用两矩形板同相或反相弯曲振动所形成的对称或反对称模态驱动导轨运动。两模态均由板的面内弯曲振动产生，一方面，只需配置弯振陶瓷片便可激发两相振动模态，简化了定子结构设计；另一方面，利用板结构振动效率较高的弯曲振动，有利于设计出大输出力和大功率的超声电机。

1 电机结构及工作原理

图1为基于弯曲模态的板形直线超声电机结构。该电机由定子、直线导轨、预压力施加装置和底座组成。图2为定子结构，它由前端盖、压电陶瓷片、电极片、夹持、后端盖和螺栓等部件构成。前端盖的两个端面均有螺纹孔，利用内六角螺栓使得前端盖、后端盖、压电陶瓷片和电极片连接为一体，构成了两个相互垂直的矩形振子。两振子关于前端盖的正对角线轴对称，驱动足位于前端盖顶点。夹持件呈L形，拐角处采用柔性圆弧连接，以降低因机械加工误差造成的装配难度。

图1 基于弯曲模态的板形直线超声电机

图2 定子结构

定子配置8片弯振压电陶瓷片，分为4对。每对弯振陶瓷片关于夹在其中间的电极片对称布置，即每对陶瓷片一侧同时膨胀时，另一侧同时收缩；反之亦然，以激发矩形板的弯曲振动。将位于同一振子上的两电极片用导线连接，构成定子的A、B相。

直线导轨用螺栓固定在底座上，导轨一边粘贴一片Al2O3陶瓷条，以提高驱动足和导轨接触界面的耐磨性。电机装配时，定子一边与导轨平行放置，夹持一端通过螺栓铰支在底座上，另一端通过预压力弹簧使驱动足紧压在陶瓷条上，为二者接触界面提供法向预压力，通过调节螺栓压缩弹簧的形变量改变法向预压力的大小。这种一端铰支，一端施加预压力的夹持方式，限制了定子的平动自由度，使得定子只能绕铰支点做微幅转动。其次，利用杠杆原理，可施加大预压力，同时保证电机输出性能的稳定。

该电机采用单模态驱动方式，分别利用如图3所示的反对称模态和对称模态，以实现电机的双向运动。在自由边界条件下，定子A、B两相施加相位差为π的正弦激励时，两振子做反相弯曲振动，形成反对称模态(图3(a))，此时驱动足沿垂直于定子对称轴的方向做往复直线运动。当驱动足在预压力的作用下与导轨接触时，考虑到驱动足处的弹性变形，驱动足上接触点的运动轨迹将变成一个倾斜的扁平椭圆轨迹[24]。接触点的椭圆运动单向地间歇驱动导轨，进而推动导轨沿oy的反方向做直线运动。同理，定子A、B两相施加相位差为0的正弦激励时，两振子做同相弯曲振动，形成对称模态(图3(b))，此时驱动足沿定子对称轴做往复直线运动并在接触状态下产生反向的椭圆运动，从而推动导轨沿oy方向运动。

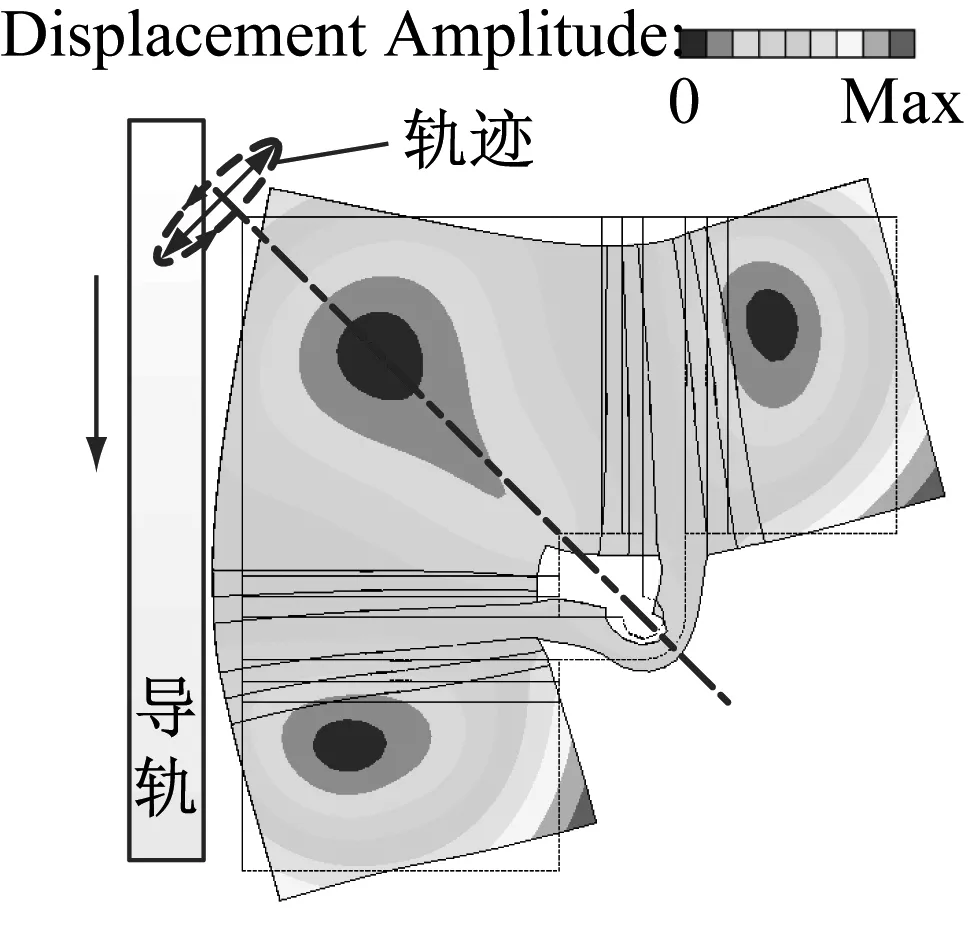
(a) 反对称模态

(b) 对称模态

2 定子结构设计

定子作为电机的核心部件，既关系到电能到机械振动能的转换效率，又关系到定子机械振动能到动子动能的传递效率。因此定子设计是整个电机设计的关键内容，它包括压电陶瓷片和夹持位置设计以及开槽尺寸设计。

2.1 压电陶瓷片和夹持位置设计

压电陶瓷片作为将电能转换为机械能的元件，对结构进行应变激振，其配置位置影响所需模态能否有效激发。夹持关系到电机输出性能的稳定。二者位置需在定子上合理配置，以提高模态激发效率，降低夹持对模态的影响。

图4为定子结构参数。定子厚度为8 mm，压电陶瓷片厚2 mm，夹持件厚度为4 mm。前端盖端面伸出长度为l1，后端盖的宽度为l2，且l1+l2=20 mm，以满足定子最大特征尺寸为62 mm的设计要求。

图4 定子结构参数(mm)

设夹持件中心位置到驱动足的距离为xc，则xc=36+l1。可见，l1的大小直接影响压电陶瓷片和夹持的安置位置，而二者安置位置需根据定子工作模态振型设计。由于定子结构复杂，难以通过理论分析获得定子的精确振型。为此借助ANSYS对定子进行模态分析，研究结构参数l1对振型的影响。提取单个振子的弯曲振型如图5所示。

图5 单个振子振型

图5表明单个振子弯曲振动时反对称模态的弯曲振型波峰(或波谷)位置(记为x1)与对称模态的弯曲振型波峰(或波谷)位置(记为x2)不重合，有一定间距。根据超声电机设计理论，压电陶瓷元件应安置在定子应变最大处。对于弯振模态，其应变最大处位于弯振波峰位置，且该处截面转角位移为0，利于安置夹持。因此应将压电陶瓷片和夹持安置在弯振的波峰或波谷处。所以设计结构时将压电陶瓷片关于夹持对称布置，以使压电陶瓷片中心位置和夹持件中心位置重合，均为xc。

由于两模态弯曲振型的波峰位置不重合，为此调节l1大小，使两振型的波峰位置尽可能靠近，并使夹持件中心尽量靠近振型波峰位置。这样设计的好处在于只需配置一套弯振陶瓷片便能有效地激发出两工作模态，同时减小夹持对模态的影响。因此可定义

(1)

来定量表示夹持件中心位置和两工作模态弯曲振型波峰位置的靠近程度。

由式(1)可以看出，Δx越小，夹持件中心位置越靠近振型波峰位置。Δx随l1的变化关系如图6所示。图6说明夹持件中心位置更靠近对称模态的波峰位置，并且Δx随着l1的增大而增大。由于需要对前端盖和夹持件间的电极片引导线焊接，前端盖的端面至少要伸出4 mm，留出空间以便于接线操作。因此确定参数l1为4 mm，此时夹持件中心位置偏离两工作模态波峰位置的平均距离为3 mm，在可接受范围内。上述参数下的定子工作模态见图3，此时定子的反对称和对称模态频率分别为25.92 kHz和28.32 kHz。

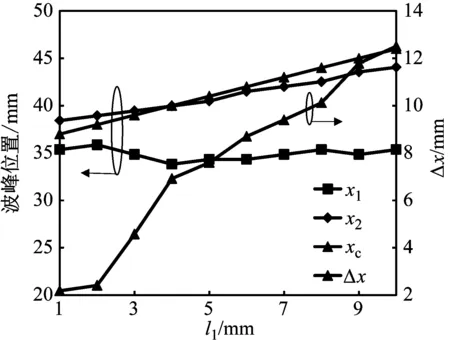
图6 振型波峰位置随l1的变化关系

Fig.6 Relationship between position of wave peak of mode shape andl1

2.2 开槽尺寸设计

由电机工作原理知，定子驱动足运动轨迹为一条倾斜直线，具有平行于定子与导轨接触界面的切向分量和垂直于接触界面的法向分量振动位移。法向分量起到使驱动足周期性地接触或脱离导轨以及提供驱动足与导轨间的动态预压力的作用；切向分量起到驱动导轨的作用。因此定子驱动足振幅大小对电机输出性能有着重要影响，提高驱动足振幅能更有效地驱动导轨，有利于提高电机的输出力和输出速度。

从电机工作模态可以看出，对称模态在驱动足附近存在振动节点，从而导致驱动足处振幅较小。利用ANSYS有限元计算，给定子施加200 Vpp交流电压信号，在工作模态频率附近进行谐响应分析，计算发现：反对称模态下驱动足振幅为3.4 μm，而对称模态下的振幅仅有0.389 μm。这说明电机由对称模态驱动时，性能将会极差。

开槽是控制振动体模态特性的一种方法。对于板状定子，采用电火花线切割加工技术对其开设通槽，加工简单易行。因此文章通过对前端盖开设通槽，改变模态特性，消除振动节点，以增加对称模态下的驱动足振幅。前端盖按图7所示的方法开槽，以前端盖右下角顶点C点为圆心，在前端盖内螺纹两侧各开一道宽度为0.5 mm，半径分别为R1和R2的90°圆弧通槽，以尽量“切断”前端盖对称模态的节点区域。

参数R1和R2确定了所开通槽的大小，因此可将其选作设计变量对开槽尺寸进行优化，即设计变量为

X=[R1R2]T

(2)

驱动足部分仅通过前端盖颈部AB和A′B′与定子剩余部位连接，考虑连接强度和避开内螺纹开槽等因素，设计变量X的优化设计空间取为

图7 定子前端盖开槽方法(mm)

D={X|R1∈[17.5,22],R2∈[8,13]}

(3)

在优化设计过程中，对定子的设计要求需通过定义目标函数来表征。设驱动足的x方向和y方向振动分量的振幅分别为Aix和Aiy，相位分别为φix和φiy，其中i=1或2，分别表示反对称模态或对称模态情况。则驱动足在对称或反对称模态下的稳态响应为

(4)

因为在定子的有限元模型中，两矩形振子完全对称，理论上驱动足在对称或反对称模态下的运动轨迹为一倾斜直线，且x和y方向的振幅相等，亦即φiy-φix=±π或0，Aix=Aiy。优化的目标是通过选择合适的开槽尺寸R1和R2，尽可能地增大对称和反对称模态下驱动足的振幅，由于Aix=Aiy，因此优化模型可表示为

(5)

式中,λi为加权系数，满足λ1+λ2=1。引入加权系数是因为设计变量对不同模态下的驱动足处振幅的影响程度也不同。

为研究变量R1和R2对两模态振幅的影响规律，利用ANSY有限元计算，得到参数R1和R2对振幅的影响如图8所示，其中图8(a)为R2=8 mm时，驱动足振幅Aiy随R1的变化规律。图8(b)为R1=22 mm时，Aiy随R2的变化规律。

从图8可以看出，对称模态下的振幅A2y要比反对称模态下的振幅A1y小，且A2y随R1的增大而增大，随R2的增大先增大后减小。参数R1和R2主要影响A2y，而对A1y影响较小。因此加权系数可取为λ1=0.2,λ2=0.8。

(a) 参数R1

(b) 参数R2

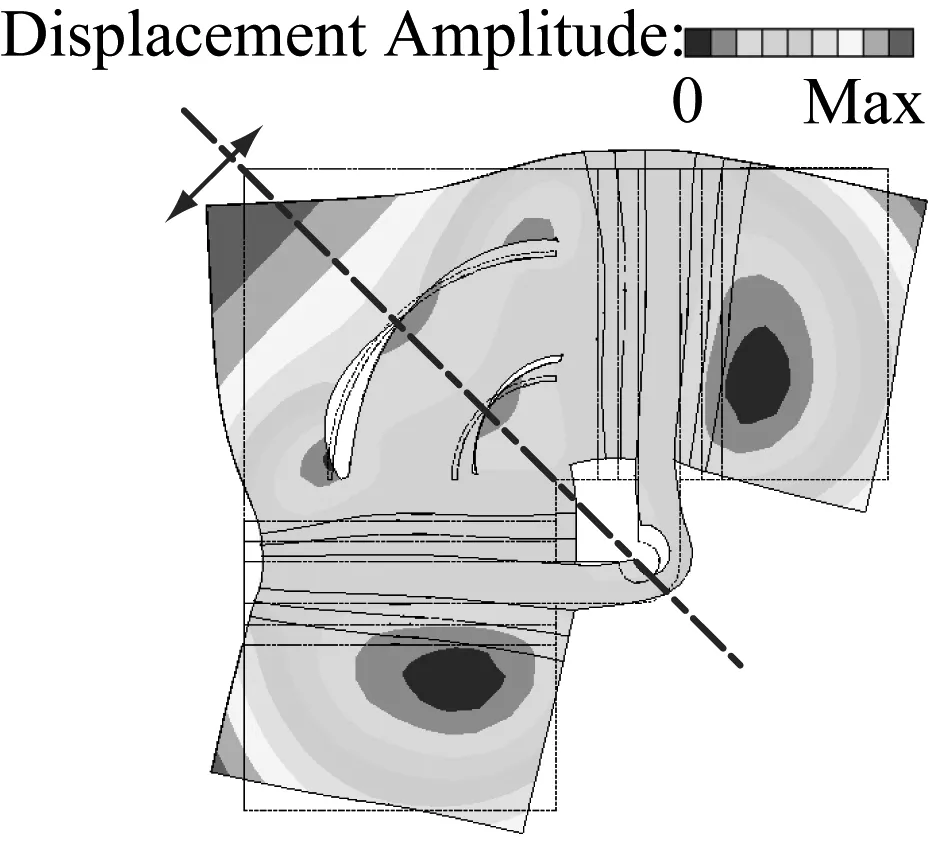
(a) 反对称模态

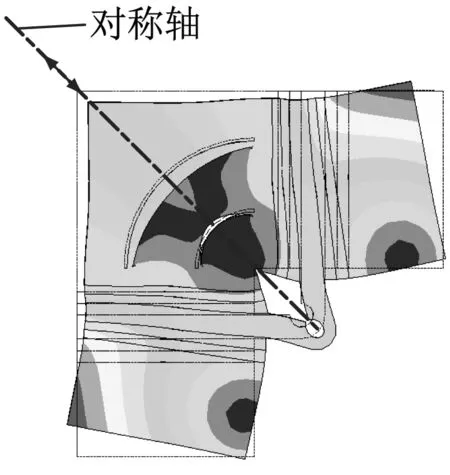
(b) 对称模态

表1为定子开槽前后定子的有限元分析结果对比。从表中可以看出，通过开槽，定子对称和反对称模态的频率略有增大，且振幅均得到了增加，其中反对称模态振幅增加了14%，对称模态振幅提高了3.6倍。对比开槽前后定子的模态(图2和图9)，通过开槽切断了前端盖驱动足附近的节点区域，从而驱动足处振幅得到增大。

表1开槽前后定子的有限元分析结果对比

Tab.1Comparisonoffiniteelementanalysisresultsbeforeandafterslotting

反对称模态对称模态f1/kHzA1y/μmf2/kHzA2y/μm未开槽25.923.428.320.389开槽后27.033.87329.161.8

3 实验研究

3.1 定子模态实验

依据有限元设计所得尺寸加工装配出未开槽和开槽后的样机如图10所示。

图10 样机照片

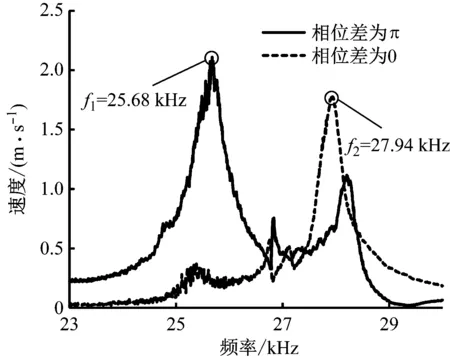
采用德国Polytec公司生产的PSV-300F-B型多普勒激光测振仪对样机进行振动测试实验。首先对定子进行扫频测试。由于驱动足表面为曲面，其法向振动不易测试，因此选择两样机的前端盖上靠近驱动足的一个侧端面作为测试面测试定子的频响特性曲线。图11为在给定子A、B两相施加相位差为π或0的80 Vpp激励电压下，定子的频响特性曲线。从图11可以看出，各样机的两条频响特性曲线分别有一峰值，对应的频率即为反对称模态共振频率f1和对称模态共振频率f2。未开槽样机的对称模态速度频响峰值很小，开槽后样机的对称模态速度频响峰值有较大增加，甚至接近反对称模态的频响峰值。

接着依次对两种样机在各自共振频率f1和f2下进行定频实验，按照图12中的测试方法测试两个测试面的振型和靠近驱动足的测试点P点沿测试面-2法向的振幅。图13为开槽后样机的振型图。图13(a)表示两振子做反相弯曲即为反对称模态，图13(b)表示两振子做同相弯曲即为对称模态，测试的振型与图9中计算的理论振型基本一致。测定P点振幅时给定子施加频率为f1或f2，相位差为π或0的80 Vpp正弦激励电压以激发定子的反对称或对称模态。两种样机的模态实验结果见表2。

由模态试验结果可以看出，通过开槽，定子对称模态的振幅有了较大提高，同时反对称模态的振幅也有所增加。与有限元仿真结果比较，定子的两相工作模态实际频率下降了1.2 kHz左右。仿真和实验结果之间存在差别，主要是因为在ANSYS仿真过程中有限元模型采用了简化，且未考虑螺栓对压电陶瓷的预压力，以及存在加工和装配误差等因素。

(a) 未开槽样机

(b) 开槽后样机

图12 振动测试方法

反对称模态对称模态频率f1/kHzP点振幅/μm频率f2/kHzP点振幅/μm未开槽24.780.827.150.14开槽后25.681.127.940.7

(a) 反对称模态振型

(b) 对称模态振型

图13 定子振型图

Fig.13 Mode shapes of stators

3.2 样机机械输出特性

图14为测试电机输出特性的实验平台。采用一台信号发生器(AFG3022B)和两台功率放大器(HFVP-153)驱动电机。电机驱动吊有砝码(作为负载)的直线导轨双向运动，导轨运动速度通过高速激光位移传感器(KEYENCE LK-H150)测得。

图14 电机输出特性实验平台

首先对未开槽样机性能进行测试。经测试，在激励电压为500 Vpp时，未开槽样机在反对称工作模态下的最大空载速度为308 mm/s(预压力为100 N);最大输出力为50 N(预压力为200 N)。但是，未开槽样机在对称模态频率附近却无法运动，即未开槽样机的对称模态由于驱动足处振幅过小而无法驱动电机。

接着重点研究开槽后样机的输出性能。图15为在预压力100 N，激励电压500 Vpp下，开槽后样机的空载速度频率特性曲线。由图15可知，在工作频率范围内，电机空载速度随频率的增大先增大后减小。反对称工作模态在频率22.8 kHz附近空载速度最大，最大速度为305 mm/s；对称工作模态在频率26.6 kHz附近空载速度最大，最大速度为329 mm/s。该电机两个方向的速度频率特性曲线还具有一个特点，在中间段的工作频率区间内，电机运行速度变化很小，基本保持稳定，说明该电机运行稳定，具有较大工作频率带宽。

(a) 反对称模态

(b) 对称模态

图16为开槽后样机在不同预压力下的机械输出特性曲线。由图16可以看出，电机的输出速度随着负载的增加而下降，而且预压力越小，这种下降趋势越急剧。适当增大预压力可提高电机的负载性能：在200 N预压力，500 Vpp激励电压下，对称模态和反对称模态可驱动的负载分别为50 N和70 N。电机定子重183.2 g，最大推重比可达38.2。与未开槽样机比较，开槽后样机反对称模态的输出力提高了40%，对称模态可较好地驱动电机，且输出力大。

4 结 论

提出了一种基于矩形板弯曲振动的单模态、大推力直线超声电机，它分别利用定子的对称模态和反对称模态实现电机的双向运动。

研究表明开槽会影响定子的振动特性，通过在定子前端盖开设两道圆弧形通槽，消除了对称模态在驱动足处的振动节点，增加了对称模态和反对称模态在驱动足处的振幅。

(a) 反对称模态

(b) 对称模态

研制了直线超声电机样机，并开展了实验研究。实验表明，通过开槽，定子驱动足处振幅和电机机械输出性能明显提高，特别是对称模态下的电机输出性能。开槽后样机最大速度和推力分别为329 mm/s和70 N。该电机结构简单、紧凑，运行稳定，推力大，可用于电机安置空间狭窄且需要大推力的直线驱动场合，有较大的应用前景。