基于改进字典学习的单通道振动信号盲源分离算法
2019-01-23曲建岭田沿平郭超然
余 路, 曲建岭, 高 峰, 田沿平, 郭超然, 李 俨
(1.海军航空大学青岛校区 航空仪电控制工程与指挥系,青岛 266041;2.西北工业大学 自动化学院,西安 710072)
盲源分离(Blind Source Separation,BSS)是机械设备进行复合故障诊断的一种有效方法。目前在机械设备的盲分离方法中,通常假设观测信号的个数不小于源信号的个数,然而这在实际的故障诊断实践中并不总是成立。受限于机械设备关键部件的安装位置和传感器的布置成本,观测信号个数小于源信号个数的欠定盲源分离问题更加普遍,而单通道盲源分离(Single Channel Blind Source Separation,SCBSS)问题可以看作是欠定盲源分离问题中的特例。由于观测信号个数越少意味着获得的可用信息越少,对于源信号的恢复越困难,因此,单通道盲源分离问题一直以来是盲源分离问题研究的热点和难点问题[1-2]。
多年来,已有众多学者对此问题展开了研究。一些学者采用经验模态分解(Empirical Mode Decomposition,EMD)及其变种理论的方法展开研究。例如,文献[3]利用EMD算法增加观测信号个数,将SCBSS问题转化为正定或超定BSS问题,再使用成熟的FastICA算法求解。为了抑制EMD算法的端点效应问题,文献[4]采用EEMD算法(Ensemble EMD,EEMD)和基于四阶累积量的特征矩阵联合近似对角化算法(JADE,Joint Approximative Diagonalization of Eigenmatrix)并成功应用于地声信号的分离。这些算法虽然在一定条件下都可以较准确的恢复源信号,但EMD算法本质的端点效应及模态混叠问题并没有得到根本的解决,同时,这些方法改变了信号的结构特征,受人工经验的因素影响较大,因此给这类算法的广泛应用带来了限制。还有部分学者考虑观测信号的稀疏性问题,文献[5]和文献[6]采用时频分析和聚类的方法解决欠定盲源分离问题,但对于SCBSS问题,线性稀疏性的条件常常不能满足,而更复杂的非线性混合问题则需要更大的运算量和新的求解算法,目前在这方面的研究还尚在起步阶段。
基于以上分析,本文采用了另外一种思路求解SCBSS问题,即将移不变字典学习算法加入到SCBSS求解问题的框架中。
具有移不变特性的稀疏编码算法最早由Smith在2006年的《Nature》中提出[7],其本质是将信号以多个基函数及其相应系数卷积的形式表示,自适应的学习蕴含在信号中的移不变基函数,从而实现对原信号的稀疏表达。对于旋转机械来说,反应信号特征的分量往往都是重复出现的,比如故障轴承的冲击,齿轮的磨损及旋翼转速异常等[8]。在恒定工况下,不同激振源的信号特征相似,不同激振源的信号有所不同。利用移不变字典学习算法(Shift Invariant Dictionary Learning,SIDL)求解观测信号中的移不变基函数,引入改进的模糊C均值聚类算法自适应地将估计源信号个数的同时,实现对各个移不变基函数时域重构移不变分量进行聚类,实现同类源信号的聚类和不同类源信号的区分,从而实现单通道振动信号的盲源分离。
1 SIDL学习算法
1.1 SIDL学习算法简介
SIDL与标准稀疏编码不同,其将输入信号y表示成各个基函数与其系数的卷积
*xj+ε
(1)
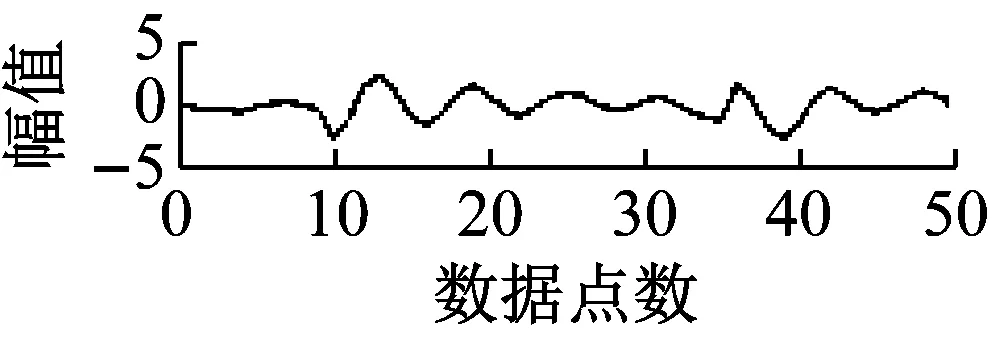
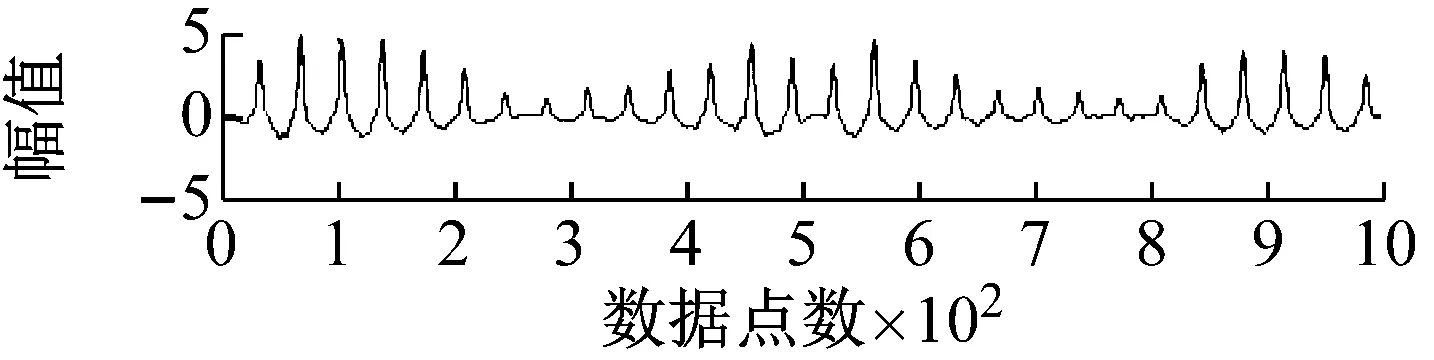
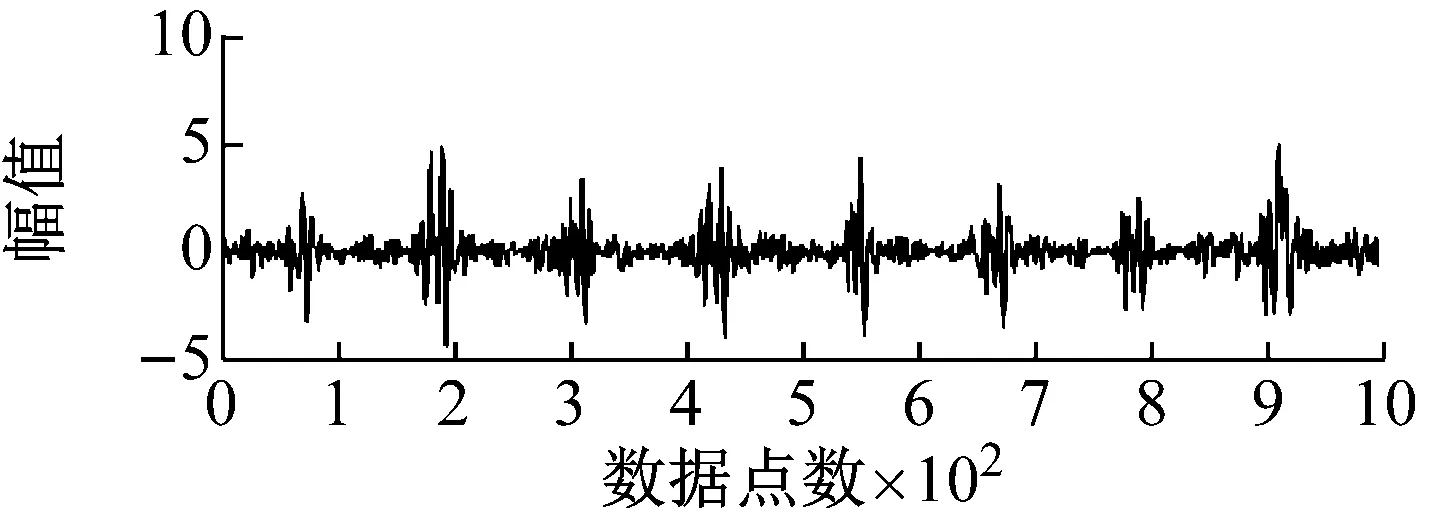
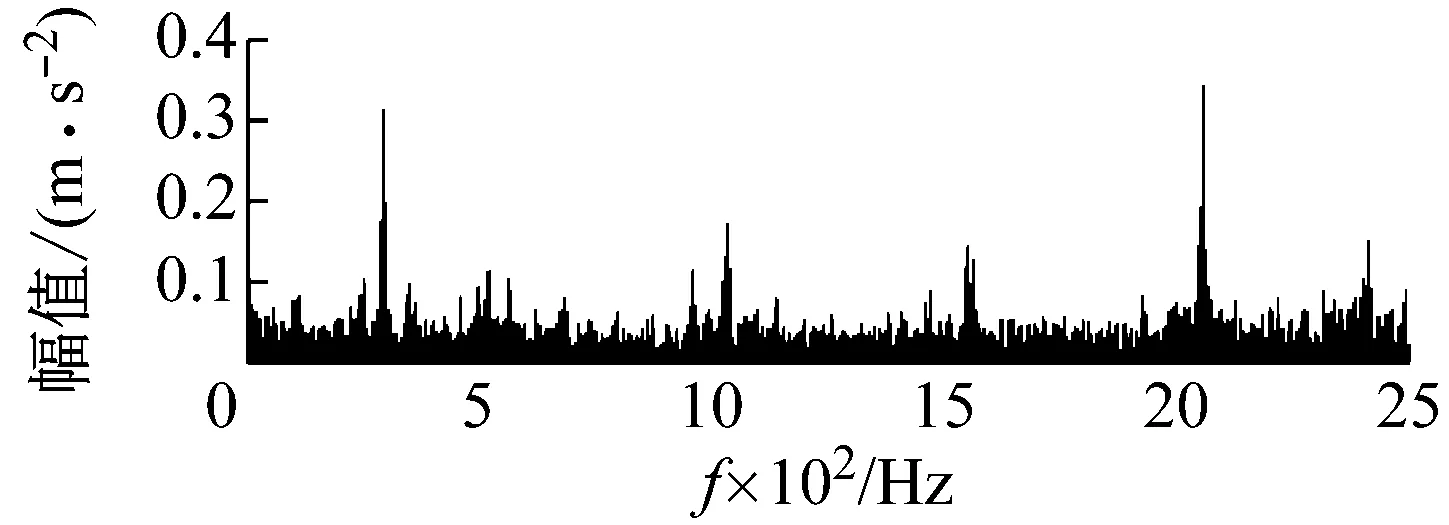
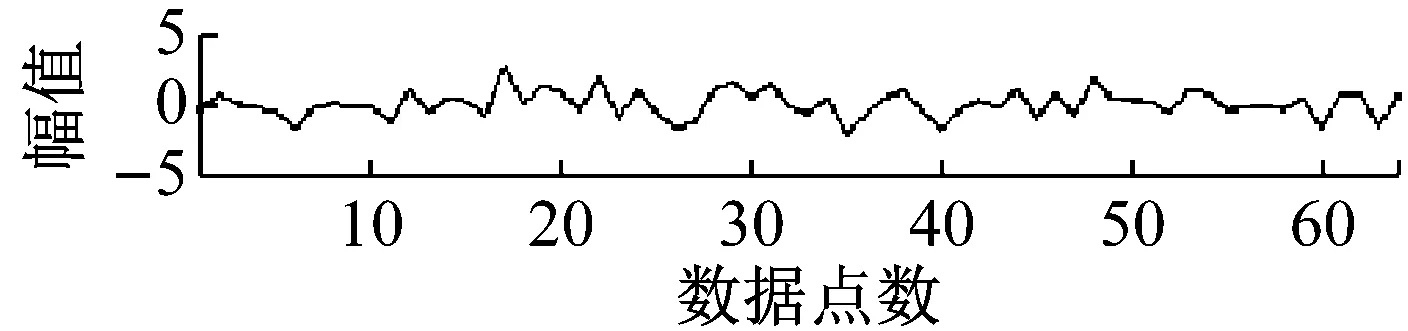
式中,“*”表示卷积算子,dj∈Rm为基函数,M为基函数个数,xj∈Rl为稀疏系数,m为基函数长度,l为信号的分段长度,n为原始信号长度,且三者满足m 求解稀疏系数的过程相当于把所有基函数固定,求解每个基函数对应的系数 (2) 在该阶段中,固定系数x求解字典矩阵D,则原优化问题转化为l2约束优化问题 (3) 式中,N为输入信号个数。直接求解上式计算量巨大,本文在字典学习阶段采用时频域转化的思想,将时域计算量较大的卷积运算转换到频域,由频域的乘积运算代替时域的卷积运算,使运算复杂度由O(N2)降低为O(NlgN),提高了运算效率。由Parseval定理可知,式(3)可转化为如下优化问题[13] (4) (5) 其中,λ∈RM为对偶变量,单位向量I∈RM,并且: (6) 模糊C均值(Fuzzy C-Means,FCM)聚类算法已被广泛应用于数据挖掘和信号分析[14],与传统的基于硬阈值聚类的算法不同,FCM聚类算法利用模糊集理论实现对数据的软划分。文献[15]指出,对于振动信号这类非平稳信号,采用软阈值比硬阈值划分往往能取得更佳的效果,因此本文采用模糊C均值聚类算法实现移不变分量的聚类。 给定数据集X=[x1,x2,…,xn]为s维空间Rs的有限观测样本,采用FCM算法针对每个数据点产生模糊隶属关系uij=ui(xj)∈[0,1]。聚类中心由采样点的数值及其隶属化目标函数的最小值确定 (7) (8) (9) 利用SIDL自学习观测信号中的移不变基函数,将各个基函数进行时域重构得到移不变分量(Shift Invariant Component,SIC),将各个SIC进行分段并提取关键点,将FCM算法对各SIC进行自适应聚类,以聚类后源信号的相关度最小作为对源信号数目的最佳估计。输出聚类后的SIC作为最终分离的源信号。 算法流程图如图1所示。本文算法的具体实现步骤如下。 图1 本文算法简要流程图 步骤1 将观测信号进行分段和平滑预处理。 步骤2 利用SIDL算法自学习信号中的移不变基函数。 步骤3 将各移不变基函数进行时域重构得到各个移不变分量(SIC)。 步骤4 求解各SIC的包络谱。 步骤5 将各SIC的包络谱进行分段并执行局部最大值检测,得到反应包络谱概略波形特征的峰值点。 步骤6 将反映波形特征的峰值进行模糊C均值聚类,聚类个数依次从2到SIC的总个数,依次计算不同聚类数下的恢复的源信号相关系数平均值。 步骤7 以相关系数平均值最低作为对源信号个数的估计,并对此时的SIC进行合并,得到分离的源信号。 在大型设备中,齿轮和轴承是重要的机械部件。当齿轮和轴承发生故障时,往往给机械设备的健康性能带来损失。因此,本文根据齿轮与轴承的故障模型,分别构造了故障齿轮信号和故障轴承信号的仿真模型[17-18],同时加以白噪声。 当齿轮发生故障时,往往表现出幅值调制与相位调制的现象,其振动信号模型为 (10) 式中,Am(t)和θm分别为第m次谐波的幅值和相位,f1为齿轮啮合频率。在本例中取M=5,Am(t)=2.5[sin(60πt)+2]/m,θm=mπ/4,f1=340 Hz。 轴承发生故障时往往伴随着振动信号的冲击响应,因此故障轴承的模型可以简化为 y2=a(t)e-ptsin(2πf2t+φ) (11) 式中,a(t)为调幅幅值,p为衰减系数,f2为轴承固有频率,φ为相位。在本例中取a(t)=20[sin(60πt)+2],φ=0,f2=3 400 Hz,T=0.01 s,采样频率fs=12 kHz。观测信号可以表示为y=y1+y2+yn,其中yn为高斯白噪声,使观测信号与原始信号的信噪比为10 dB,源信号与观测信号如图2所示(为了更好的展示细节,各个信号取1 000个点,下同)。应用本文提出的字典学习算法,设置参数如表1所示。 图2 源信号及加噪混合信号 参数数值基函数长度50基函数个数6子信号长度256子信号重叠率50%稀疏度160迭代次数60 经过60次迭代后算法收敛,学习到的基函数及其对应的移不变分量(SIC)如图3所示,从基函数中可以隐约看出,故障轴承的冲击响应与故障齿轮的调制特性,但从对应的SIC中可以比较明显的看出两种故障已经实现了区分。为了以数值计算的方式而不是主观臆断作为两种故障区分的依据,考虑将各个SIC转化至频域,采用包络谱对其进行进一步分析。 由于采样点数以及采样频率的原因,原始包络谱呈现出凌乱复杂的波形,不利于后期的处理分析。因此本文提出了局部最大值检测的处理策略,即将包络谱进行不重叠分段处理,以每一区间段内的最大值点作为关键点,将所有关键点平滑连接形成了易于理解与处理的包络谱波形特征,同时波形的峰值关键点可以作为接下来模糊C均值聚类的特征向量加以分析处理,如图4所示。考虑到信号源个数的未知性,本文采取自适应的源信号数目估计,即将聚类个数从2开始逐一增加到预先设定的基函数个数,在每个聚类数目下执行模糊C均值聚类得到源信号的估计,若达到理想的分离效果,则分离的源信号之间的皮尔逊相关系数的均值达到最小。在本例中,聚类数目与分离的源信号相关系数均值(corrmean)的关系如图5所示,可以看出,当取值为2时达到最小值,这也符合本例的实际情况。 图3 学习到的基函数及其对应的时域移不变分量 图4 各个移不变分量的包络谱(实线)及局部最大值检测(虚线)的结果 Fig.4 Envelope spectrums of SICs(line) and results of local maximum detection(dotted line) 图5 聚类数与corrmean关系 聚类数目为2时分离的源信号的时域波形如图6所示。从图中可以看出,分离效果良好,保留了故障轴承和故障齿轮的主要特征信息,只是在波形的幅值上与原始信号存在一定的出入。 图6 本文算法分离结果 作为对比,分别以文献[3]和文献[4]的方法进行实验,实验结果分别如图7和图8所示,可以看出并没有达到良好的分离效果。为了定量衡量本文算法与其他算法的分离效果,采用峰值信噪比(SNR)和均方差(MSE)作为指标参数,不同算法的实验结果如表2所示。可以看出,本文算法在三者中保持最高信噪比的同时具有最低的均方差,表明本文算法较好的保持了源信号的特征。 图7 EMD+ICA法分离结果 图8 EEMD+JADE法分离结果 为验证本文算法在实际装备中的可行性,将其应用于某型直升机振动数据采集与处理。众所周知,直升机的飞行安全至关重要,一旦机体发生故障将会给机组人员的生命和装备造成损失,因此常利用振动信号传感器采集机体各位置处的振动信号作为故障诊断的依据,但受限于直升机各部件的紧凑性,单个传感器采集到的信号可能是多个机体振源的叠加,因此有必要对其进行分离作进一步的判断。直升机部分振动传感器的安装如图9所示。 表2不同算法分离效果对比 Tab.2Comparisonofseparatingresultsofdifferentmethods 方法y1y2SNRMSESNRMSEEMD+ICA(文献[3])2.88.353.55.38EEMD+JADE(文献[4])5.23.954.34.46本文算法13.51.0514.21.21 将位于右发动机前部的振动传感器采集到的信号作为研究对象,其时域波形和频域包络谱如图10所示,从图中无法看出明显的特征。设置基函数个数为4,其余参数与表1相同,应用本文的字典学习算法学习到的基函数如图11所示,对其时域重构的移不变分量(SIC)进行包络谱分析及局域最大值检测,实验结果如图12所示。从图中可以看出SIC1与SIC3的包络谱略有相似,SIC2与SIC4的包络谱也有相似之处,为了验证猜想,应用模糊C均值聚类算法,聚类个数从2到4,发现在聚类个数为2时达到corrmean最小值,因此判断采集到的振动信号包含2个信号源。 (a) 观测信号时域波形 (b) 观测信号包络图 图11 学习到的基函数 图12 各移不变分量的包络谱及局部最大值检测 Fig.12 Envelope spectrums of SICs and local maximum detection 分离的时域信号如图13所示,对各个分离信号求取包络谱如图14所示,可以看出分离信号1为慢车时右发动机转子的转速fm(293 Hz),分离信号2为减速器齿轮振动信号(fc,2fc,3fc,4fc)。因此该振动传感器采集到的信号已成功得到分离,一旦某部位发生故障异常振动时可以准确定位到具体的位置。 (a) 分离信号1时域波形 (b) 分离信号2时域波形 (a) 分离信号1包络图 (b) 分离信号2包络图 作为对比,分别将文献[3]和文献[4]的方法应用于上述实验数据,分离后信号频谱分别如图15和16所示。 (a) 分离信号1包络图 (b) 分离信号2包络图 Fig.15 Envelope spectrum of separated signals by paper[3] (a) 分离信号1包络图 (b) 分离信号2包络图 Fig.16 Envelope spectrum of separated signals by paper[4] 通过分离信号的包络谱对比可以看出,文献[3]和文献[4]方法均一定程度上存在两种信号源混叠的现象。例如,文献[3]中的分离信号1中含有减速器齿轮振动信号的各阶谱,但也部分含有右发动机转子转速的频率,给分离信号的识别增加了困难。同理,文献[4]方法的分离结果也存在类似的问题,表明分离效果较本文算法存在差距。 取三种算法各运行20次的平均运算时间结果进行对比,实验软件环境配置采用Linux系统下Matlab2014a,硬件环境采用i5HQ6300处理器,8 GB内存。实验结果如表3所示。 表3 不同算法运算时间对比 不可否认,文献[3]和文献[4]算法相比于本文算法具有更快的运算速度,本文算法的时间花费主要在于移不变基函数的迭代求解,但通过迭代求解的移不变基函数可以更好地学习到观测信号中存在的本质特征,因此可以获得更佳的信号分离效果。 本文提出了一种采用改进字典学习对单通道振动信号进行特征自学习和盲源分离的解决方案。移不变字典学习算法能够自学习反映信号本质特征的移不变基函数,解决了特征提取依赖专家知识与人工提取的困难;以局部最大值检测算法提取各个移不变分量的包络谱关键点,降低了后期聚类运算的效率和准确性,而且更有利于反映频域信号的波形特征;利用自适应模糊C均值聚类算法实现对源信号的恢复,解决了源数估计和信号恢复的问题。由仿真和实测数据的实验结果可知,本文提出的算法具有较高的源信号恢复精度,有利于对单通道振动信号的进一步分析,具有较强的工程应用推广价值。1.2 系数求解

1.3 字典学习
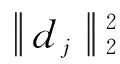


2 模糊C均值聚类算法

3 基于改进字典学习的单通道振动信号盲源分离算法

4 实验验证
4.1 实验设置




4.2 仿真实验



















4.3 实测航空发动机振动信号实验



















5 结 论
