基于位置补偿系数距离估计的滚动轴承特征损伤敏感性评估算法研究
2019-01-23王之海柳小勤
王之海, 伍 星, 柳小勤
(昆明理工大学 机电工程学院 云南省高校振动与噪声重点实验室, 昆明 650500)
滚动轴承是旋转机械的重要元件之一,在旋转机械故障中,滚动轴承故障占比可高达30%[1]。滚动轴承状态监测数据可获取其疲劳损伤信息,可有效避免因突发失效而造成的经济损失甚至人员伤亡。采用声发射技术可比振动方法更早的获取滚动轴承疲劳损伤信息[2],多采用不同特征的趋势来分析其疲劳进程。
不同的特征可从不同方面反映滚动轴承的疲劳状态,需采用较多指标方可较为全面的描述其损伤情况,而较多数目的特征集不一定就比少数的特征集获得更好的识别效果[3],且特征维数过高将增加计算负担,增添时间成本,同时也增加了特征集中可能存在冗余或不相关性等低敏感性特征的风险。因此需开展特征评估以筛选有效、敏感特征,在降低计算成本的同时,提高特征集对损伤程度的识别精度。
特征评估方案采用评价准则来评估各特征的敏感程度。主要可分四类,即距离评估、信息评估、依赖性评估以及一致性的评估方法[4]。其中,基于距离的评估方法因具有简单、直观、易实现以及高效等优势[5-8]而被广泛应用于机器学习、数据挖掘以及模式识别等领域[9-11]。该方法在滚动轴承方面的应用中,多采用振动数据,不利于对初期损伤的识别;且对故障特征敏感性的研究较多[12-16],而对损伤特征敏感性的研究相对较少[17-18];对人工故障的研究居多,对自然疲劳失效的研究较少。
针对上述问题,本文深入剖析了现有距离评估方法的不足,提出了一种基于位置补偿系数距离估计的滚动轴承声发射特征损伤敏感性评估方法(Position Compensation Coefficient Distance Evaluation Technique, PCCDET),较全面的分析了干扰滚动轴承损伤敏感性识别精度的因素。随后,对来自自制滚动轴承疲劳试验台不同损伤程度的声发射信号开展了试验研究,并与现有的典型距离估计方法进行了对比,验证了本文提出算法的有效性。
1 基于距离估计的特征评估
1.1 距离估计理论
距离估计理论的实质在于通过考察各特征的样本在类内与类间距离的表现,以衡量各特征的重要程度。这些表现主要体现在样本类内的聚合特性与类间的离散特性这两个方面。若某类内越多的样本间的距离越小,则说明该类越紧凑,也就有越好的聚合特性。反之,则说明该类的聚合特性越差。同样的,若某两类间越多的样本间的距离越大,即类间离散度越大,则说明该特征对这两类差异性的识别能力越强。通常将二者综合评价,即类内聚合特性越好,类间离散度越大,则特征的敏感度越高。
Yang等[19]提出了距离估计技术(Distance Evaluation Technique, DET),并将其应用于旋转机械的特征提取研究中,有效的提高了故障诊断准确率。随后,Lei等[20]对DET方法进行了改进,提出了基于补偿因子的特征评估方法(Compensation Distance Evaluation Technique, CDET),通过引入补偿因子来补充描述各特征的表现,并以此对敏感度进行修正,较好的实现了滚动轴承故障类别与损伤程度的聚类识别。近些年,吴瑕等[21]又提出了一种基于聚类与几何的特征评估方法,相对前两种DET方法,该方法对类内聚合度、类间离散度的描述更为细致,并考虑了各状态间的重合关系,将两圆间的几何关系引入,对各特征类间的分离度修正,进一步完善了DET方法,并在弹道目标识别方面取得了较好的效果。上述三种DET方法虽然各有优势,但仍存在一些不足,现总结至表1。
由表1可知,目前的DET方法中仍存在抗干扰能力不足的问题,野点的存在将影响特征敏感度的准确评估。而声发射信号的非平稳与易混入噪声的特性将可能导致信号产生更多的扰动。且上述方法较少考虑各类间的重合性,考虑了重合性的DET方法也因仅适用于圆形簇而降低了算法的通用性。
1.2 基于位置补偿系数距离估计的特征敏感性评估算法
结合表1中各DET方法的不足,本文提出了一种基于位置补偿系数距离估计的特征评估技术(PCCDET),算法的实现步骤如下
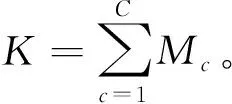
(1) 规格化处理,抑制特征在不同量纲等级的影响
(1)

与文献[21]略有不同,此处规格化去掉了绝对值步骤,这样可在不改变原数据固有特性(如各特征样本的波动性等)基础上获取规格化数据。
(2) 计算第c类第j维特征的样本距中值dc,j
dc,j=median({|qm,c,j-ql,c,j|})
(2)
式中,符号median表示对集合取中值。此处采用了中值计算,可有效避免数据的波动干扰,即使无数据先验知识的情况下仍可增强算法抗干扰能力,可更好的描述绝大多数样本距的平均水平。
(3) 计算第c类第j维特征中心uc,j
uc,j=median({qm,c,j})
(3)
此处采用中值同样为抑制干扰,避免因野点而导致类中心的偏移,可更好的表明类中心位置。而均值通常确定类的质心、重心,而并非类的中心,不能有效避免野点的干扰。
(4) 计算第c类第j维特征的样本至中心距中值fc,j
fc,j=median(|{qm,c,j-uc,j}|)
(4)
同样的,式(4)代表了绝大多数类内样本至类中心的距离水平。
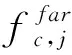
(5)
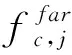
在有y个野点的情况下,则待选最远点数为
N=y×2+1
(6)
如在有2个野点的情况下,则需用5个最远点(2×2+1)方可较好地逼近原数据半尺度。当然,若已有野点数先验知识,也可直接剔除野点。但通常情况下,事先并不清楚野点数目。因此采用保守试探方式的中值方法(式(5))可更好的探寻贴近有效半尺度的最远点,也可更有效的降低误选风险(式(6))。
(6) 定义第c类第j维特征紧密度tc,j
tc,j=dc,j+fc,j
(7)
上式综合性的说明了第c类第j维特征样本的紧密程度。
(7) 计算全部C类第j维特征平均紧密度tC,j
(8)
tC,j值越小,说明该特征类内样本的平均紧密程度越高。
(8) 计算第j维特征全C类样本距中值的平均dC,j
(9)
由该式可获取全部C类样本之间距离的平均紧密程度信息。
(9) 计算第j维特征全部C类样本的中心Uj
(10)
(10) 计算第j维特征各类中心至全类中心的距离均值fU,j
(11)
(11) 计算第j维特征平均类中心距dU,j
(12)
式中,c,e=1,2,…,C,且c≠e。采用该式可获取第j维特征样本的类间平均离散程度信息。
(12) 定义并计算第j维特征的类间离散度sC,j
sC,j=fU,j+dU,j
(13)
计算结果sC,j表明了第j维特征样本的平均分离特性。
(13) 定义并计算第j维特征的位置补偿系数pj。首先定义pce,j为第j维特征中类c与类e间的位置关系因子,其数学描述如下
(14)
其中,c,e=1,2,…,C,且c≠e。为弥补文献[21]对非圆形簇考虑的不足,本文作者提出采用两类中心距与这两类等效半尺度和的差作为这两类位置关系的修正参数(即式(14))。修正系数的不同取值代表着不同的位置关系,其对应关系如下:
① 分离
若两类中心距比各对应簇的等效半尺度和大,则说明两类状态之间完全可分,即pce,j>0。该值越大,可分性越好。
② 相交
若两类中心距不大于各对应簇的等效半尺度和,则说明两类状态之间可能存在相交特性,即pce,j≤0。该值越小,可分性越差。
随后,将全部pce,j均值ptj作为第j维特征的位置补偿系数,见式(15)
(15)
为方便计算,将已获取的J个位置补偿系数进行归一化,见式(16)。
(16)
由式(16),得到位于区间[0,1]的归一化位置补偿系数,并以此修正各特征的敏感度。
为说明采用等效半尺度方法判定不规则簇间的位置关系比采用等效圆的方法(文献[21])具有更好的优势,在此采用简易图示进行问题说明,由于篇幅所限,仅举一例分析,如图1所示。
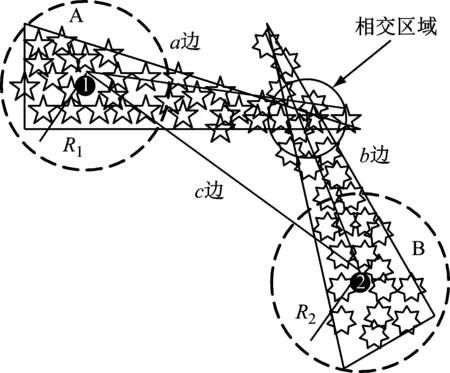
图1 不规则簇位置关系判定
图1中,类A与类B为三角形不规则簇,其等效圆心(带序号的深色圈)更偏向于样本密集处。各类等效圆半径分别为R1与R2。随后,分别连接最远点(灰色填充点)与对应圆心并连接这两个圆心,得到三条边,即a边,b边与c边。
① 等效圆方法
图中可明显看出两类属于相交关系,相交区域已用蓝圆圈出。但用等效圆方法判定这两类的位置关系为相离,这与实际不符。
② 等效半尺度方法
采用本文提出的等效半尺度方法进行测定,很容易发现,根据几何中两边之和大于第三边的准则(a+b>c),即中心距<等效半尺度和,由式(14),可得出二者位置关系为相交。
通过上述说明,可见相对于等效圆方法,采用等效半尺度方法将有助于对不规则簇位置关系的判定。
(14) 对第j维特征进行评估,最终得到第j维特征敏感度αtj
(17)
式(17)综合地考虑了各维特征类内的紧密度与类间的离散度,并依照各类位置关系修正了特征敏感度。
(15) 归一化
(18)
经归一化处理,特征敏感度处于[0,1]范围内,方便了后续的观察与计算。αj值越大,该特征敏感性越强,反之则越弱。
2 试验与分析
2.1 滚动轴承疲劳试验
为检验算法的有效性,本文作者在自制滚动轴承疲劳试验台(见图2)上开展了试验研究,并随机选出滚动轴承分别处于初始运行阶段、轻微损伤阶段、点蚀阶段以及剥落阶段的9组声发射数据作为算法验证的待测试数据源。这四个阶段的声发射数据也反应了滚动轴承的四种不同损伤程度。

图2 滚动轴承疲劳试验台
由图2,测试系统采用PAC-WD传感器拾取滚动轴承声发射信号,采用电涡流测量仪拾取轴承转速。与上述传感器配套的采集卡分别为PCI-9846H型采集卡(台湾凌华)以及NI-USB-9234采集卡(美国NI)。声发射信号采样率设置为1 MHz。试验过程中,电机保持600 r/min的转速。待测试轴承型号为SKF-51115的推力球轴承。
每组随机抽取的数据集由4×100个样本组成,即从四个阶段中各抽取100样本而构成。各阶段的典型声发射波形如图3所示。
2.2 特征敏感性评估
为较为全面的获取滚动轴承损伤信息,分别从时域、频域对数据集样本进行特征提取(见表2)。表2中各参数的物理意义及公式详见文献[22-24]。

表2 特征参数
由表2,最终得到400×28的特征矩阵。随后按1.2小节给出的PCCDET算法步骤开展特征敏感性评估。经试验观察发现,野点个数大多在4个以内,为更为稳妥的得到有效半尺度,根据式(6)将待选最远点数增大为10,各特征敏感度分析结果见图4。
(a) 初始运行阶段
(b) 轻微损伤阶段
(c) 点蚀阶段

(d) 剥落阶段
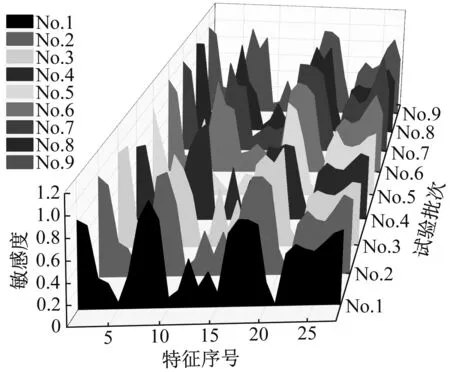
图4 各次试验特征损伤敏感性评估结果
由图4,在这9次试验中,各特征在不同批次试验中的敏感度表现大致相同。较好的特征在历次试验的特征评估结果中的敏感度大多具有较高值,而较差的特征敏感度值大多较低。
随后,对全部批次试验的特征敏感性分析结果求平均,以获取各特征的平均敏感性表现,各特征对应的平均敏感度值见表3。

表3 特征平均损伤敏感度
由表3,方差、有效值、能量计数、均方根谱、均方谱以及频域方差等参数在多次算法测试中,均具有较好的损伤程度识别能力。而频域峰值频率历次试验的平均敏感度却较低,表现最差。
2.3 识别精度对比验证
特征评估最终目的是为找出关键特征集。若集合中特征维度越小,分类识别精度越高,则说明选出的这些特征越好,评估方法越有效。
为进一步说明算法的有效性,将全部特征按各自敏感度递减排序,从敏感度前2特征集直至全部的28特征集以特征数逐步增1的组合方式,分别与DET、CDET以及聚类几何的特征评估算法同等组合方式得出的分类精度对比,以考察PCCDET算法在不同特征维度下保持高识别精度的鲁棒性。具体的对比方案流程如下:
步骤1特征评估。分别采用DET、CDET、聚类几何的方法以及本文的PCCDET方法评估各特征的损伤敏感性,并分别获取按敏感度降序特征矩阵的前2,前3…至全部的28敏感特征集。
步骤2LibSVM计算。采用LibSVM分类器对上述方法筛选出的各敏感特征集进行分类识别精度验证。分类精度计算方法采用10折交叉验证法。
步骤310折交叉验证。
为防止由于设定百分比不同而出现盲目乐观或悲观的情况发生,本文采用了更为严谨的10折交叉验证法计算分类精度。
10折交叉验证的过程为,将原始样本特征集数据随机分成10份,每份数据再以随机训练样本数进行分类器模型训练,而将该份其余部分作为测试样本进行分类器模型的测试。通过上述过程计算每份的分类准确率,最后将全部10份的分类准确率汇总求平均,得到算法最终的分类精度。
按上述流程,不同方法对损伤的识别精度对比结果,如图5所示。
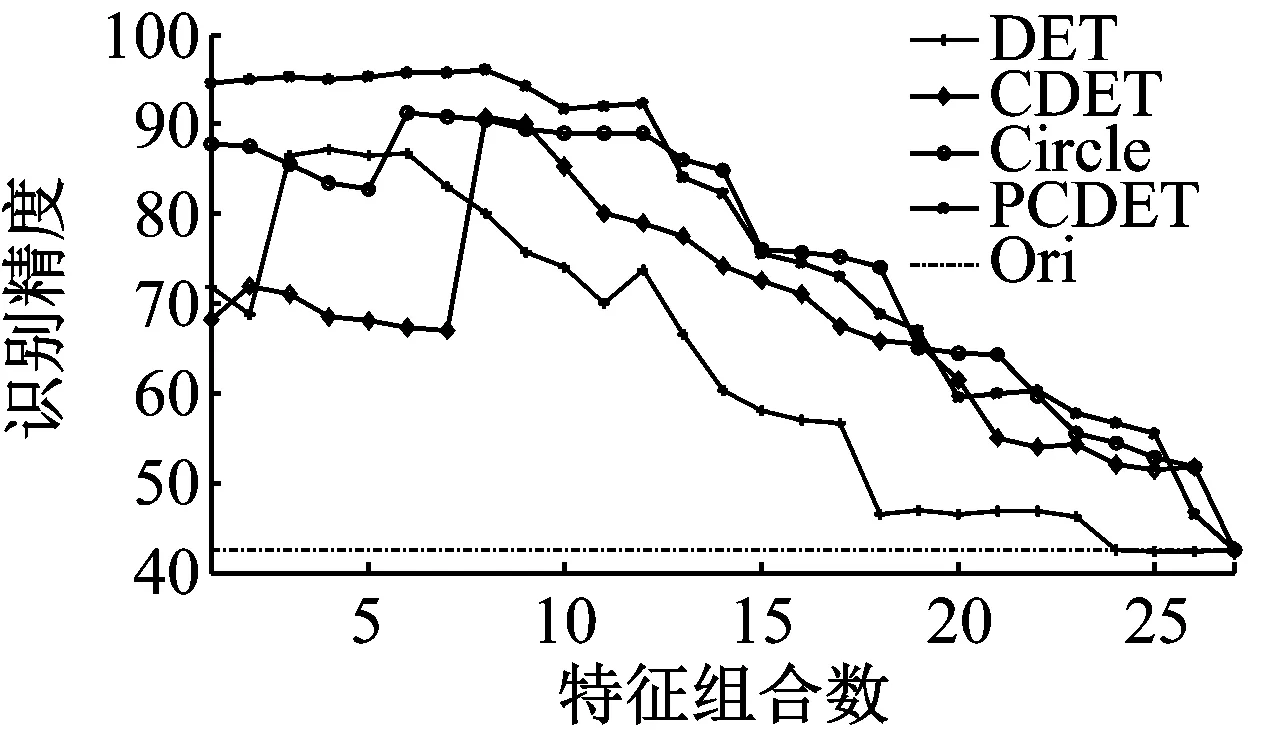
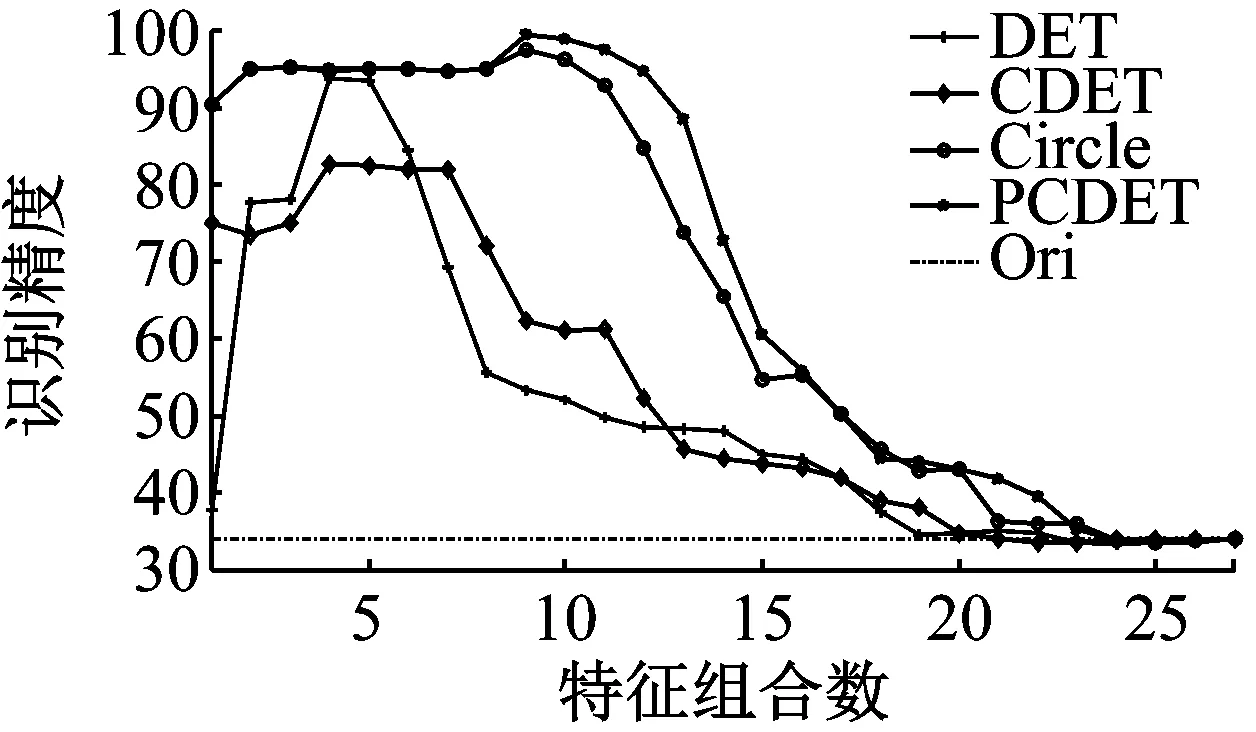
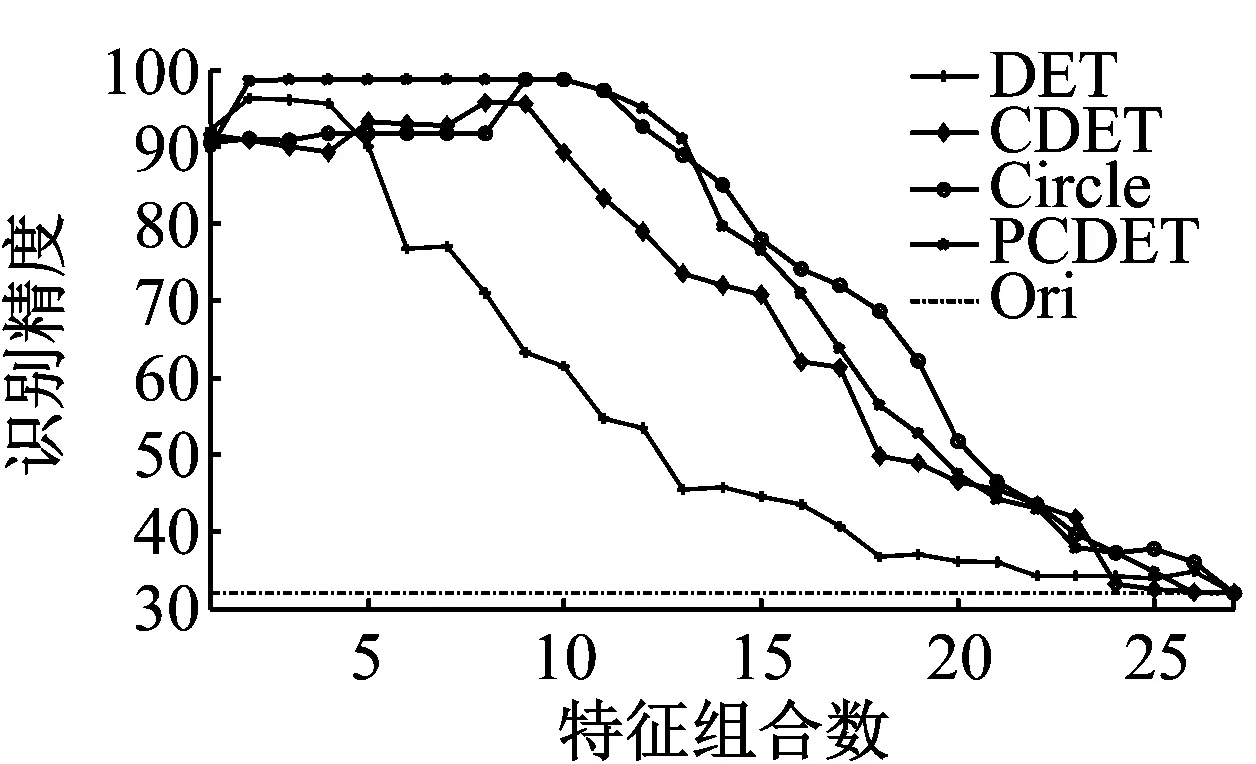
图5为采用各评估方法在不同原始精度条件下的损伤识别精度对比结果。图中,点划线为原始特征集(即采用全部特征)的识别精度。图5(a)中,原始精度约为72%。②图为①图的局部放大(椭圆)。图5(b)、(c)与(d)分别为原始特征集精度约为42.5%、34%与32%时,各算法的识别精度对比。从对比看出,DET方法表现最不稳定,CDET相对DET方法较为稳定,但在绝大多数情况下相对于聚类几何的方法精度较低,而PCCDET算法能够相对更快地筛选出合适的敏感特征集,可在不同维度特征集下,以相对更大的概率保持较高识别精度,具有更好的稳定性。
按上图顺序,即按原始数据精度分别为72%,42.5%,34%与32%的特征矩阵顺序,各算法的识别精度与最佳特征组合数对比,见表4。
由表4,相对其他DET方法,PCCDET方法不论从特征组合平均识别精度,以及最大识别精度的角度来看,该方法均具有更好的表现。对于最佳特征数指标,来自原始精度42.5%与34%(对应图5(b)与图5(c))的计算结果表现较差,出现该结果的原因可能在于原始数据分类精度过低,而对算法产生一定干扰。此时,其他算法也存在类似情况,如图5(b)中,虽然DET算法与聚类几何算法更早的达到最高分类精度,但在最高分类精度之前的走势混乱,无明显规律。而本文方法仍能在此过程中保持相对稳定,且仅其初始精度就已超越其他各算法的最佳精度。在图5(c)中,PCCDET方法同样能相对稳定地达到最高精度,且在该稳定阶段内,也保持了更高的精度。

(a)
(b)
(c)
(d)
为验证本文算法相对传统算法鲁棒性的改善,本文采用来自不同原始精度的数据的平均准确率来评价各算法的鲁棒性。平均精度越高,则说明算法在不同数据类型条件下保持高精度的概率越大,即算法保持高精度结果的稳定性越好,也就是算法的鲁棒性越好。该平均准确率可由表4的第一项指标结果求平均得出,计算结果如表5所示。
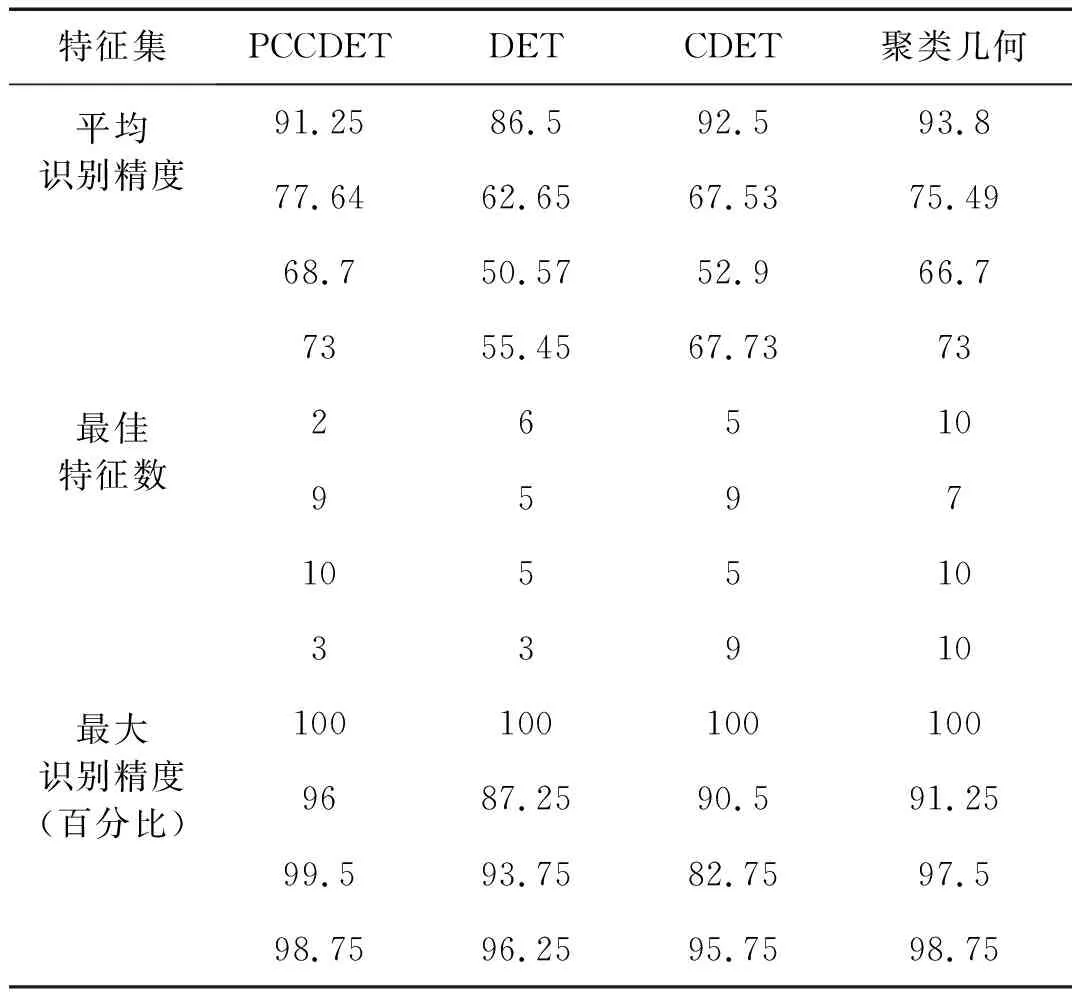
表4 各算法识别精度与最佳特征数对比

表5 各算法的鲁棒性
由表5可知,由PCCDET算法计算出的平均精度值最高,则说明相对其他方法,该方法的鲁棒性最好。这一点从图5中各子图中采用PCCDET算法结果的波动性效果也可明显看出,尤其是从初始精度到最高精度的过程。
3 结 论
本文提出了一种基于位置补偿系数的距离估计算法,解决了采用距离估计方法对干扰滚动轴承损伤敏感性识别精度的因素考虑不足而影响其评估性能的问题,以及多指标间存在的不相关或冗余干扰滚动轴承损伤程度信息的有效获取问题。
研究表明,本文算法可提升对目标识别的准确性、通用性与鲁棒性,对各特征敏感性的考察更为全面,能有效筛选出对滚动轴承损伤敏感的特征。相对其他DET算法,本文方法能更为稳定的保持较高的识别精度,筛选出的敏感特征集能够更好的提供滚动轴承损伤信息。
