基于多体动力学方程的考虑关节润滑的机械系统模型

蔡菲

(西安航空职业技术学院 航空制造工程学院， 710089)

0 引言

在科技不断发展进步的过程中，机械科学也不断朝着全新的方向发展。轻质、高速、低噪音及智能化等是我国现代机械主要的发展方向及标志，并且也为机械科学工程提出了较高的要求，从而也引出了一系列的机械力学课题。比如，在机器速度不断提高的过程中，能够提高其惯性作用，从而产生噪声、振动等一系列的问题，对机器寿命及工作性能造成影响。并且，还会因为弹性变形影响到机械系统，使机械系统和传统机械动力及运动特点不同。所以，要想能够有效满足现代机械需求，就要使机械的动态性能进一步提高，还要能够解决系统动力学的问题。多体系统动力学是与结构动力学、经典动力学、计算机技术及控制理论相互结合的学科，被广泛应用到高速机构、机器人及航天航空方面，属于现代力学使用过程中最为活跃的内容。在机器人系统中，关节具有轴承之间的相互摩擦，传统装置齿轮的间隙和谐波减速器等多种问题。目前，柔性关节问题备受相关研究人员的重视。

1 多体系统力学方程

多体系统是指利用部分相互连接的转动缸体及位移组成，其的表达式为：

其中M表示质量矩阵，q指的是加速度矢量，r指的是乘子矢量，r和结构关节约束反力是对应的，Q指的是广义外力，其中主要包括系统的摩擦力、碰撞力、外载荷及重力等[1]。

以上公式因为积分误差会导致系统的位置和速度方程存在违约的问题，那么为了能够避免此种问题的出现，就要利用约束违约稳定方式实现，简单来说，就是能够在其中融合修正因子衰减违约量，通过下式表示：

Φqq-λ-2αΦ-β2Φ=0

通过修正约束就能过得出稳定动力学方程：

其中Φ=(dΦ)/(dt)，α和β是比0要大的修正系数，一般为5-50之间，从而能够提高违约修正的效果[2]。

2 多体系统动力学模型

创建系统动力学模型，首先要对模型之间的精度进行保证，寻找数据正确的传输方式，几何模型能够在三维建模软件中创建，那么本文就使用参数化建模方式软件创建几何模型，计算软件使用多体动力学软件和大型有限元计算软件协同工作。为了能够实现动力学分析的精准性，要基于预修正模型实现仿真，然后利用系统参数的测量和仿真结果进行对比，之后修改模型[3]。

2.1 创建柔性关节

在系统中融入柔性关节模型的表示方式主要使用扭转弹簧表示。其被广泛应用到线性柔性关节，在扭转弹簧属于线性弹簧的时候，能够实现扭转弹簧扭转刚度系数的直接设置，并且也可以使用其表示非线性的关节模型，为了不使其他的非线性问题提高，那么就使用线性扭簧实现柔性关节的定义。

2.2 柔性体修改

对于结构来说，要利用模拟分析得到固有特性，从而实现结构动力学的分析。并且，系统固有特性还能够为系统动力学分析之前打下基础。机械系统在不同状态和位置的时候，其振型及频率也会出现变化，那么在修改柔性体参数的时候，就要全面观察系统模型，掌握结构及系统稳态联系，从而寻找修改参数。利用系统振型图可以看出来，系统第一节模拟具有接近第一阶段模态振型，因为系统运行，所以其位置改变系统振型差别比较小。

因为系统会为不同柔性体赋予非线性刚体自由度，假如柔性图自身具有刚体模型，在求解的时候就会具有奇异解，但是部分刚体模态固有频率会因为误差联系不为0，这个时候的软件就不能够自动判断，要求能够自行关闭[4]。图1为系统在第一阶段及第二阶段的模型。

图1 系统在第一阶段及第二阶段的模型

2.3 模型测量

以仿真为基础实现曲柄滑块实验台指导，利用对电机刚度的提高，使其转速波动能够在3 r/min以内，从而保证仿真结果收敛性。那么，整个机构就不再施加载荷。之后通过测量结果可以看出来，导致各个测量指标出现变化的主要激励就是施加驱动，激励能够导致构件出现共振，那么就无法使构建固有频率出现响应[5]。

在得到仿真结果之后，就要修正系统模型，从而提高系统精准度。首先，修正模拟阻尼比。设置缺省模拟阻尼比，得到摆杆顶端a点位移、加速度和速度，通过结果表示，因为模态阻尼比较小，所以高频响应衰减较快。其次，修正柔性关节参数。在之前模态阻尼比修正过程中，其中的扭簧及阻尼刚度系数都是0，以此表示，在模拟阻尼比为0.001的时候，实验结果与仿真结果接近，这个时候就能够逐渐修正扭簧刚度及关节组织。扭转弹簧对弹性力矩进行定义，此力矩代销及方向和零件相对角速度及角位移具有密切的联系[6]。

3 数值算例

首先，对测量仪器范围进行确定。摆杆设计的主要目的就是能够扩大实验柔性，从而能够方便测量，使测量过程中误差影响的精度能够降低，为了寻找合适摆杆测量的厚度，可以利用动力学仿真实验台实现。电机选择是实验过程中的主要部分，为了能够寻找较为 合适的转矩及转速，利用动力学仿真能够有效寻找匹配数据，以此对电机型号精心确定。表1为摆杆及连杆选择不同转速及载荷中的输入扭矩。如表1所示。

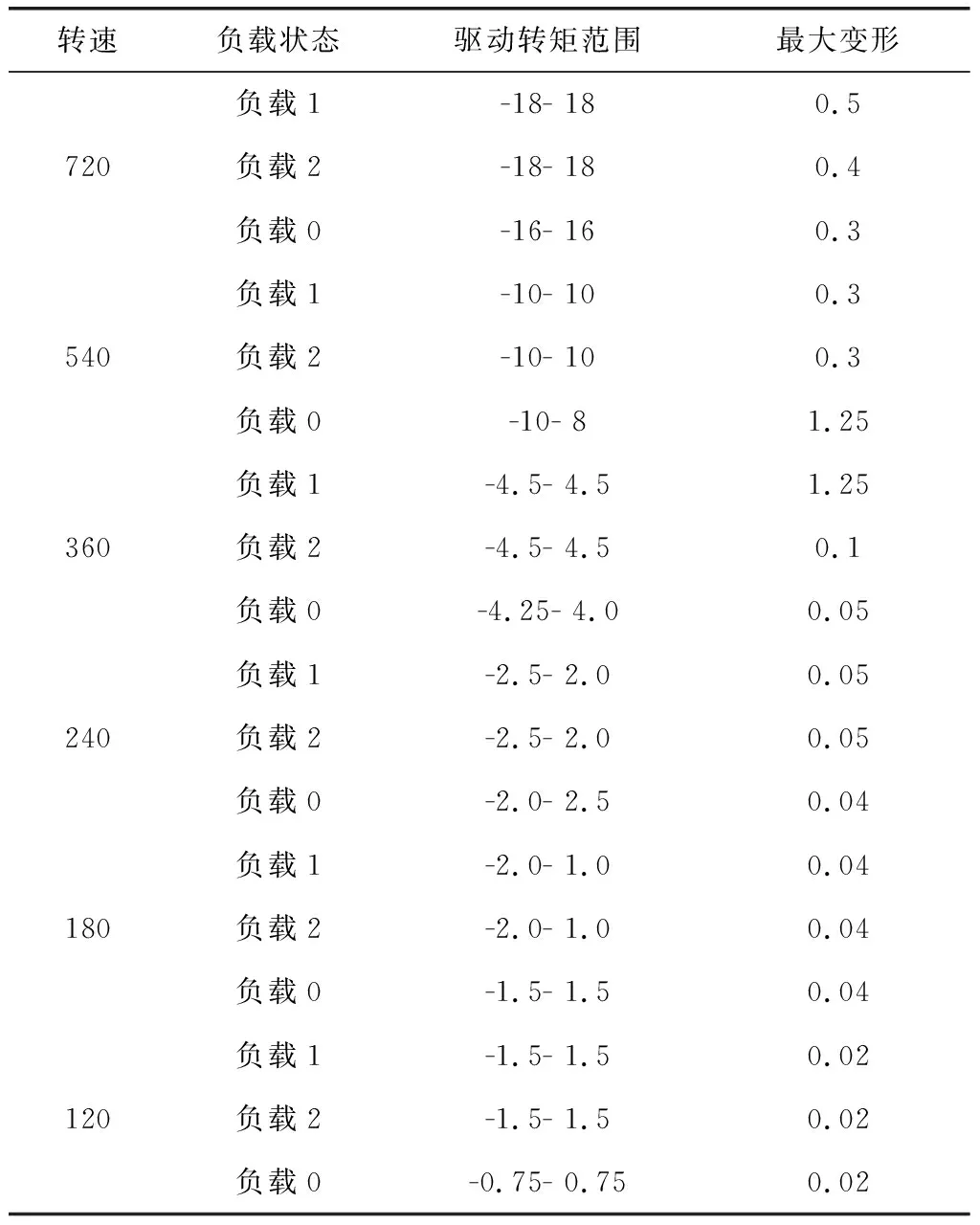
表1 摆杆及连杆选择不同转速及载荷中的输入扭矩

在实验过程中，为了能够得到弹性振动位移，不仅要使用加速度二次积分，还要使用应变法对柔性梁弹性振动位移进行测量。将经典曲柄滑块结构为例，此机构通过曲柄、连杆、滑块及机架构成，如果滑块和连杆之间存在间隙，那么还要对润滑进行全面的考虑，其他运动都属于理想的关节，为了简化动力学分析，就要假设所有的构建都属于理想关节[7]，其仿真参数详见表2。

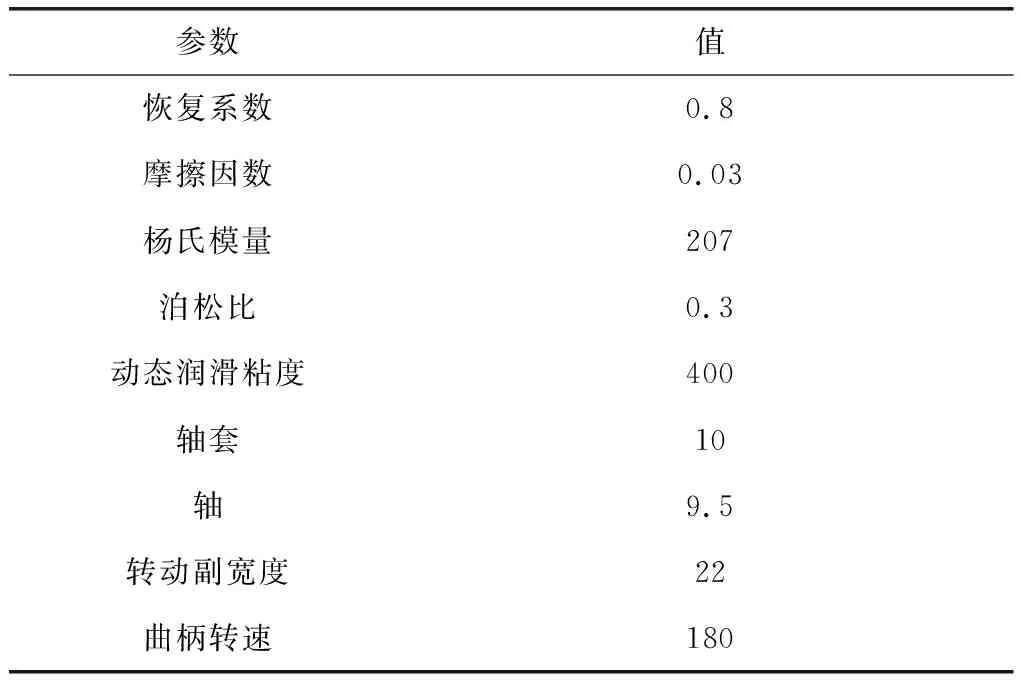
表2 模型仿真的参数

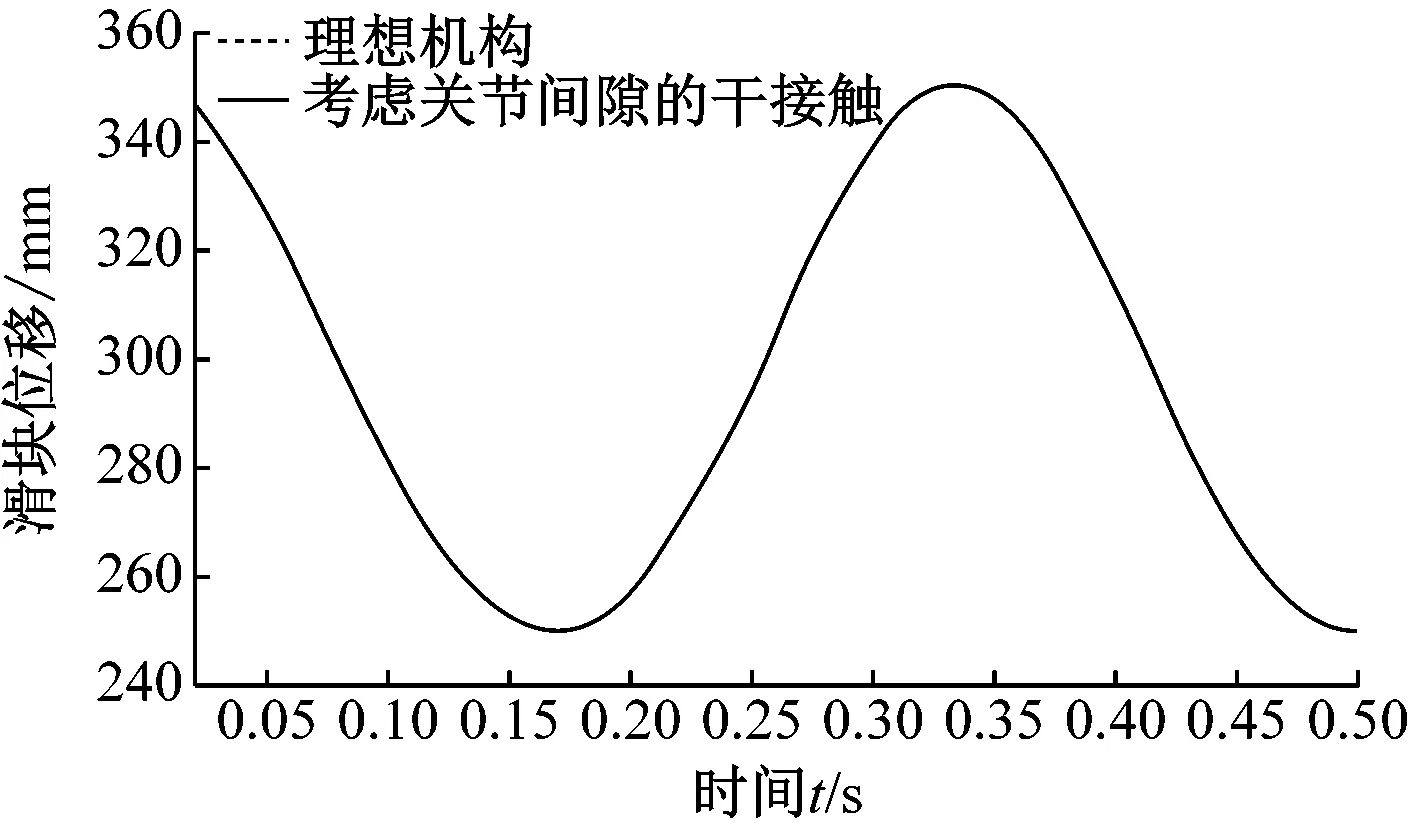
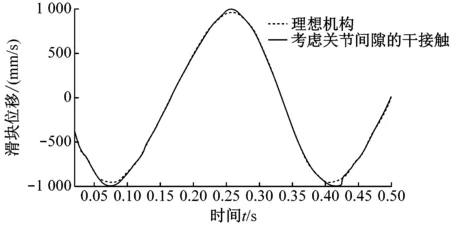
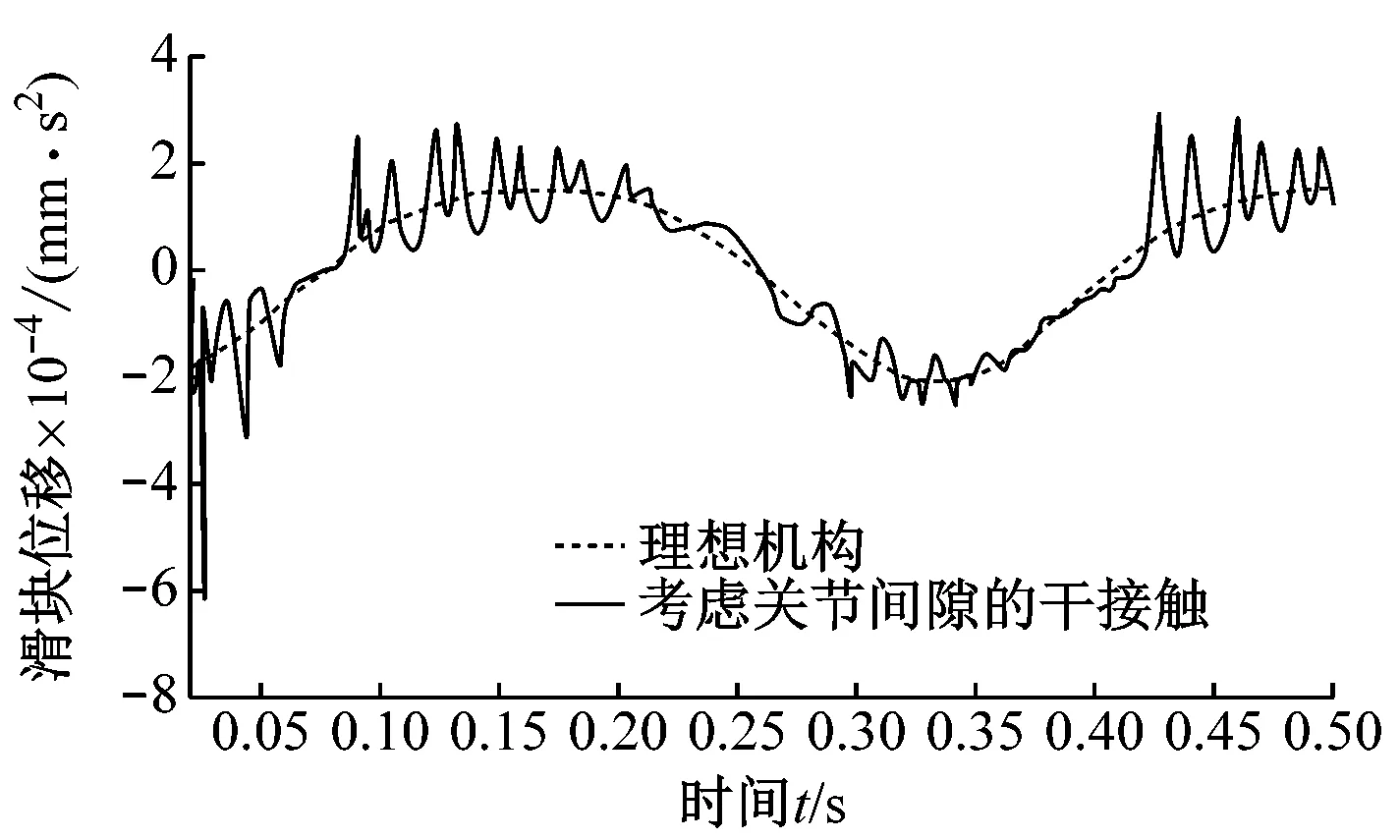
图3指的是曲柄滑块结构在对关节间隙考虑时候的滑动动态特性，如图3所示。

(a)

(b)

(c)

图3(a)指的是关节间隙没有影响到滑块的位移特点，图3(b)指的是滑块的速度并不考虑关节的间隙，图3(c)指的是关节间隙严重影响了滑块的加速度。间隙关节会使接触碰撞力的滑块加速度曲线具有大幅度的增加，并且此机构在同时全面考虑润滑及间隙时候的滑块特点为对速度及位移并没有什么影响。在不完全考虑关节润滑的时候，机构滑块加速度曲线具有大幅度高频的震动，使此机构的动力学性能有了严重的退化，并且和干接触关节反力进行对比，要对润滑后关节反力的降低进行全面考虑，这也就是要全面考虑间隙关节润滑时候的此种行为中的关节元素具有碰撞，从而抑制了加速度曲线震动的幅值。润滑动力耦合作用会使润滑机械系统中部位的受力均匀，使零部件最大的受力降低，全面考虑摩擦及润滑，能够使零部件动力学特性具有较大的影响。以此表示，此变化对于关节润滑剂系统的动力学性能和摩擦学特性具有一定的影响[8]。

4 总结

本文基于全面考虑关节润滑及间隙，全面分析了机械系统动力学性能。在不对关节润滑考虑的时候创建间隙关节元素接触力，利用多体系统动力学方程创建机械系统动力学模型，最后通过讲述平面曲柄滑块机构对比间隙关节是否具有机构润滑动态特点。通过结果表示，间隙关节没有影响到滑块的速度和位移，但却影响了关节反力和加速度。间隙关节要对润滑全面考虑，不会影响位移和速度，关节反力及加速度特点的抑制明显，在全面考虑关节润滑时候的机构动力学性能和理想状态更加的接近。