一种改进的路径选择算法研究*

年伏宝 华江林

(安徽新闻出版职业技术学院 安徽合肥 230601)

无线路由协议按照其发现和寻址方式的不同可以分文表驱动路由协议和按需驱动路由协议。它们的区别在于路径发现的需求不同，表驱动路由协议会实时或者定期更新每个节点的上网络拓扑表，实时计算该节点到所有节点的路径；而按需路由协议则是在有业务传输需求是发起路由发现请求，寻找传输路径。这两类路由协议的原理和实践表明，表驱动路由会长期占用无线信道带宽和处理器计算负重，但是实时性好，而按需驱动路由则最大限度的降低带宽和处理器资源消耗，而实时性就要略逊一筹，所以根据网络结构和业务实时性需求，要适当的选取路由协议。由于网络节点功能的差异性和网络环境的复杂性，文章研究的是一类基于时分多址(time division multiple access，TDMA)协议的无线非对称无中心自组网络，网络节点比较集中，通信(数据、视频和话音业务)频繁。该网络中路由协议的发现过程需要定期的在几个时隙周期里完成，文章的重点在于根据网络中各节点的邻节点表为业务提供路径信息，以及该邻节点表的变化情况，建立一个路由发现、路径计算模型，以达到提高带宽利用率、实时网络拓扑和降低算法复杂度的目的。

1 节点发现并将网络拓扑结构转化为带有权值的有向图

在TDMA网络中，各节点会在自己的发送时隙将自身的邻节点信息以(本地节点编号、邻居节点编号和通信权值)的形式向周边节点广播，并在本地存储邻居节点的信息，直至广播收敛或到达时间上限。为了加速发现协议的收敛，满足无线网络中继需要，路由协议要求节点发现协议在规定的时间周期内(有限个TDMA时隙周期)完成，否则邻节点信息表可能无法实时的描述当前网络拓扑信息，特别是节点运动的无线网络不止受节点的通信性能和距离影响，还对网络所处的信道环境相对敏感。对于相对稳定的(即网络拓扑在发现协议收敛时间相对稳定)网络而言，在发现协议收敛之后，各节点需要根据其所知道的邻节点信息，通过表1所示的二维矩阵来描述该有向图，该步骤的算法复杂度是0(n2)，根据文章的描述对象，该矩阵描述的是一个稠密图，文章所有的算法均以此为基础。

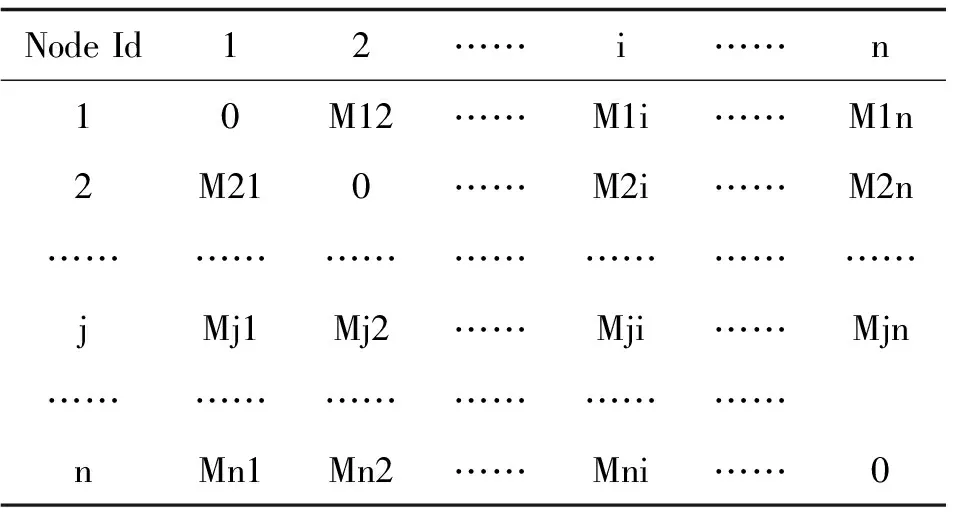
表1 二维矩阵描述网络拓扑

表1中，Mij表示节点j到节点i的通信权值，权值的定义直接反应了信道模型、通信业务需求以及节点功能性能等多方面信息，之后会具体描述。对于有向图而言，Mij一般不等于Mji。一般来讲，在有限次节点信息广播之后仍然无法获取其信息的节点，本地节点可以默认为是无法到达的，这些节点可以通过其他补充路由算法来实现节点通信。

2 计算本地节点到其他节点的路径

实践表明，无论是表驱动路由还是按需驱动路由，计算路径算法的复杂度主要体现在这个步骤上，为了找到最优的路径，几乎要遍历整张图，即时间复杂度为0(n2)。针对研究的网络模型，文章算法采用基于广度优先搜索的方式，参考按需驱动的方式，将路径计算分割成几个部分，在兼顾实时性的同时，在一定程度上降低时间复杂度。

2.1 主体算法结构

(1)根据表1中描述的网络拓扑，每一列表示该节点的直接邻节点，其值表示该节点到邻节点的通信权值。算法从源节点开始，遍历其所有的直接邻节点并将它们纳入临时节点池(tempNodePool，tNP)，并以结构体(preNode，metric，level，curNode)保存至全局结构体数组变量(GlobalNodePool，GNP)中，并给其已经遍历过的标识visited。

(2)以临时节点池tempNodePool的节点为遍历对象，逐个寻找其邻节点，计算出到该节点的通信权值，如果其邻节点遍历标识为unvisited，更新其权值并将其纳入GlobalNodePool和tempNodePool，并将其标记为visited；如果该节点为visited，而且重新计算的权值不小于GlobalNodePool中该节点的权值，表示该路径劣于已知路径；反之，就根据当前(preNode，metric，level，curNode)结构更新GlobalNodePool中该节点信息，并将其纳入tempNodePool。另外，对于已经在GlobalNodePool中的节点，如果其通信权值不大于tempNodePool中任意节点的通信权值，并标记其状态为nodeReady，表示该节点的最优路径已经找到，之后再遇到该节点，直接忽略。

(3)重复步骤(2)，直到下列情况发生时，终止遍历：①tempNodePool中没有可以继续遍历的节点；②遍历次数到达网络要求的中继级数上限。

整个遍历过程图如图1所示。对于一般表驱动路由算法而言，其每次网络更新后，都要计算出到各个节点的完整路径。而文章所提算法的主要思想是，将整个路径算法尽可能分解成多个步骤，结合按需路由算法的低消耗的优势，在实际业务需求产生时，再计算出完整路径。如此则在业务实时性允许的范围内，降低算法的复杂度。

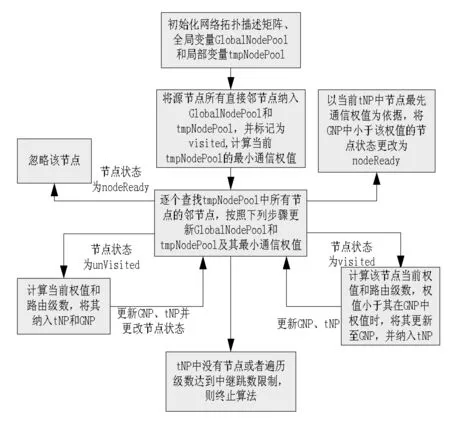
图1 广度优先算法流程图

2.2 主体算法优化

从图1可知，该次计算只是根据当前的网络拓扑状态以及网络中继级数要求，计算出源节点能到达所有节点，而并没有计算出实际路径，这是在综合考虑到文章研究的无线网络中的业务需求。经过仿真分析，该步骤的算法复杂度小于o(n2)，为了降低遍历的重复性，该算法提出了两个规则：

(1)通过添加节点状态来降低节点的重复查找次数。实际上对于稠密图而言，各个节点的连通性极高，通信链路的可达性导致各节点会重复计算多次。所以引入节点在遍历过程中的状态能很大程度降低其遍历的重复性，特别是对于平稳网络信道而言。

(2)根据中继级数需求，降低遍历级数，加速算法收敛。

该步骤在整个网络结构完成更新时直接更新，以尽可能实时的反映网络的当前结构，实际上对于通信信道相对稳定的网络而言，这是非常有利的。

3 根据业务需求计算路径信息

上述步骤耗费整个选路算法时间复杂度的大部分时间完成了算法的大部分工作，参考按需路由的特性，文章可以将后期的寻址过程独立出来，根据业务需求完成单播和广播的寻址，减少一定程度的计算。在有单播业务需求时，本地节点从GNP中找到业务的目的节点，直接逆向查找，直至找到源节点，就完成了整个路径的选取。可见这个算法复杂度是小于o(n)的。至于广播报文亦是如此，根据GNP中的level变量，从小到大依此取出，即为源节点业务广播的路径，以避免成环。

4 权值模型的定义和网络拓扑的稳定性

一般来讲，权值模型是在综合考虑网络结构、业务需求、信道质量等诸多因素之后建立的一个相对稳定的参数模型，其为优化网络通信性能提供了坚实的基础和可靠的保证。如何建立权值模型不仅是多次实验室仿真，也是外场试验的尝试性设计。文章为了优化和简化权值模型，通过仿真和对比，选取丢包率ρ，路径级数L，网络稳定性P来确定一类比较通用的通信权值模型W来描述单跳信道质量，如式1所示：

W=ρ*(1+r)*P

(1)

式中，r代表了路径级数等效系数，即每增加一跳中继，其权值不仅仅单纯增加相邻两节点的通信权值，还有相应的系数加成，以描述无线通信中减少中继路径长度带来的传输稳定性和网络资源的消耗；ρ以系统内部计算为准，例如某一小段时间内的丢包率；P则是通过周期性的节点信息扩散形成的网路结构矩阵的变化情况来描述网络的稳定性，该值的意义一方面用来参与权值调整，另一方面也为节点信息扩散周期作为参考，即网络相对稳定时，可以拉长扩散周期，以节省网络带宽和算法计算复杂度，反之则需要缩短扩散周期，以提高网络拓扑的实时反应。

网络的稳定性定义为网络连接拓扑随时间变化情况，主要包括无线信道本身受到电磁环境、空间遮挡和多径、多普勒频移等导致的变化和节点本身通信性能的改变，算法本身不做任何调整和补偿，只是尽可能的实时反应当前的网络拓扑，已确保计算出的路径的可靠性。无线网络信道的时变特性决定了网络的稳定性只是相对的，但是利用这种相对的稳定性是可以降低算法复杂度的，所以对于激变的网络处理才是整个算法的核心。根据按需路由的原理，激变网络选取按需路由是可以解决路由问题的，或者减小扩散周期，根据网络时变特性的相关性，针对多业务网络时，这样也是更好的办法。见图2。

5 改进算法的优点和不足

文章以表驱动路由为基础，结合按需路由中按需方式来一定程序的降低算法的平均复杂度，然后根据研究对象提出一类相对通用的通信权值模型。在测试工作中，不断的调整各个模型的参数以期反应网络本身的通信特性。试验还发现，由于试验中网络节点数相对少，这种优化情况并不明显，只在仿真结果引入大规模的网络节点时才能显示一定的性能优势。针对节点信息扩散周期和权值模型的构建，节点信息扩散周期是在综合考虑网络节点拓扑的实时性、计算复杂度和扩散的收敛时间等因素决定的，要精确确定该值是需要大量的仿真和试验测试的。至于通信权值模型则是比扩散周期更为复杂的模型，其受影响因素更多，文章也只是选取几个模型需求的重要参数来构建。

6 结束语

综上所述，文章在解决路径选择算法复杂度的问题上，对比按需驱动和表驱动的特性，提取各自的优势是取得了一定的效果的。然而针对这类网络结构本身提出的扩散周期和权值模型的研究依旧不够深入，而且针对各类专用无线网络越来越重要的今天，这类深入研究也更有意义。