弱耦合对耦合映像集体动力学行为的影响

张 玢

(渭南师范学院 网络安全与信息化学院，陕西 渭南 714099)

0 引言

耦合混沌系统在实际系统中广泛存在，如生态系统、神经网络、化学反应系统、物理系统，以及社交、金融、工程等许多领域。[1-2]通常情况下，耦合会使系统行为同步化。对耦合混沌系统同步的开创性研究始于1990年，Pecora和Carroll[3]在实验中实现两个耦合混沌系统的同步，提出混沌同步的方法，并讨论混沌同步轨道的稳定性。自此，科学家对耦合混沌系统的同步化进行了大量研究。研究发现，随着耦合强度和动力学内禀属性的不同，耦合混沌系统的同步行为会表现出不同的形式[4-6]，如完全同步[7-9]、广义同步[10-12]、相同步[13-15]、部分同步[16-18]、时滞同步[19-21]等等。

然而，在弱耦合的情况下，系统会展现出一些奇特的现象。Zhou Yin-zuo小组在研究基于无标度网络的耦合逻辑斯蒂映像时，研究了弱耦合时系统的集体动力学行为。[22]随着耦合强度的增加，对于选择两带混沌融合后的分岔参数的系统而言，作者发现了以下两个有趣的现象：第一，在耦合强度非常弱的情况下，发现系统最大李雅普诺夫指数突然减小，这意味着系统的集体动力学行为会变得更加有规律，进一步研究表明，系统处于延迟相同步状态，并且每个节点的时间序列都是周期五。有意思的是，在该区间之外，没有表现出周期行为。因此，稳定的周期五轨道是由相邻节点之间的弱耦合引发的。第二，对于弱耦合区域，耦合不足够引发全局相同步，因此会存在许多方向相集团。一般而言，集团的个数会随着耦合强度的增加而不断减少。但作者观测到，随着耦合强度的增加，方向相集团的个数在不断增加，直到大于临界耦合强度时，集团个数才会不断减少。笔者在基于模块网络的耦合逻辑斯蒂映像的研究中，也发现存在一个弱耦合强度区间，该区间内系统处于延迟相同步状态，并且每个节点的时间序列都是周期五的。

总结两篇文章的相同点，相同的动力学系统，相同的耦合方式，均发现了系统在一定的弱耦合强度下处于延迟相同步状态。不同点为网络不同，动力学的参数虽然不同，但都处于一带混沌区，系统表现出周期行为所处的耦合强度区间不同，随着耦合强度的增加，方向相集团个数的变化规律不同。由此可见，弱耦合对系统的影响非常复杂，但又具有一定的共性，该课题的研究应引起足够的重视。然而, 以上研究均局限在特定动力学参数、特定网络结构下，并未做系统性研究。由此引发思考:动力学参数不同时，弱耦合对系统的影响是否相同；网络结构不同时，弱耦合对系统的影响又是怎样的。本文引入一个序参量来刻画系统的集体行为，基于耦合映像格子，在弱耦合时，对动力学参数做系统性研究。基于不同的网络结构时，该序参量也能够准确判断出系统方向相的状态，并与Liu小组和笔者的研究结果相印证。

1 模型

笔者采用周期边界条件的二维耦合映像格子，每个格点的动力学行为满足如下方程：

xt+1(i,j)=f(xt(i,j))+ε[f(xt(i+1,j))+f(xt(i-1,j))+

f(xt(i,j+1))+f(xt(i,j-1))]/4。

(1)

其中：ε为耦合强度，f(x)为每个格点的动力学方程，选择逻辑斯蒂映像，采用的系统尺寸为L×L(L=100)。

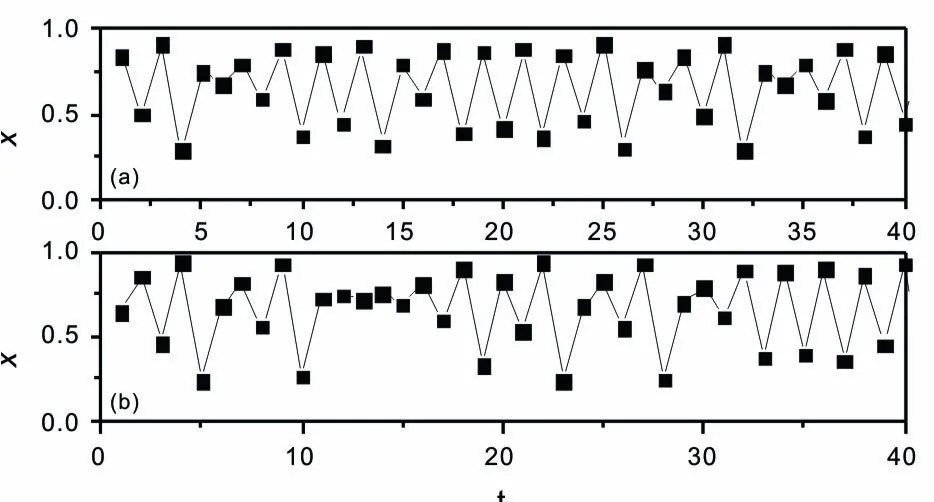
对于逻辑斯蒂映像f(x)=μx(1-x)，μ是其分岔参数，μ∈[1,4]，并且0

(a)分岔图； (b)序参量r和分岔参数μ的关系

研究表明，当μ<μ1时，x的迭代遵循一个向上方向连着一个向下方向的规律。当μ>μ1时，会出现连续两个向上方向。[23]基于此，作者引入了方向相的定义。对于格点i，如果t+1时刻x的值大于t时刻x的值，表明它处于向上相位，并标记为“+1”；反过来则表明处于向下相位，标记为“-1”。用St(i)表示方向相，其定义如下：

(2)

2 数值模拟

本文主要研究弱耦合对系统集体行为的影响。分别用序参量r和格点的时间序列来描述系统的集体动力学行为,序参量的定义如下:

(3)

为了得到更多的认识，先对单映像时μ与r的关系进行研究，如图1所示。从图1(a)可以看出，在μ1处，出现了两带融合的现象。该处的融合是由于不稳定周期一轨道和混沌吸引子碰撞所引起的混沌危机。[24]对于μ<μ1，r=1，表明系统处于方向相有序状态，从x的时间序列图2(a)中可以看到，系统只存在一上一下的方向相。对于μ>μ1，r=0，表明系统处于方向相无序状态，存在连续两个向上的方向相，如图2(b)所示。与此同时，对应周期窗口处，r有非零值。

(a)μ=3.65； (b) μ=3.75

对单映像有了一定的了解之后，再考虑二维耦合映像格子(公式(1))。图3描述了对于耦合映像格子在不同耦合强度下，序参量r随着μ的变化关系。从图3可见，随着耦合强度的增加，存在临界分叉参数μc，在该处r值突然变为0。从图3中还可以看出，μc随着耦合强度的增加而增加。另外，周期窗口的参数区间，随着耦合强度的增加不断变化，直到ε=0.017时，周期窗口完全消失。由此可见，利用序参量r，可以有效地识别系统方向相所处的状态，并且能够准确地判断出分岔参数的临界点，以及周期窗口所在的分岔参数区间和所需耦合强度大小。

图3 不同耦合强度下序参量r与分岔参数μ的关系

进一步研究发现，弱耦合对系统集体动力学行为有3种类型的影响，下面通过x的时间序列来具体刻画。第一类，无耦合时系统方向相无序，有耦合后先处于周期状态，随着耦合强度进一步增加，方向相又变为无序状态。选取μ=3.866举例说明。从图4中可以看出，当ε=0时，任意3个相连格点的方向相处于无序状态。然而耦合强度有微弱增加时，如ε=0.013，系统就会处于周期运动状态。随着耦合强度进一步增加，ε=0.017，系统的方向相又变为无序状态。

参数为μ=3.866，耦合强度分别为(a) ε=0； (b) ε=0.013； (c) ε=0.017

第二类，无耦合时系统方向相无序，有耦合后变为有序状态。以ε=3.7为例，从图5可以看到，当耦合强度从0增加到0.016时，系统的方向相从无序变为有序状态。

参数为μ=3.7，耦合强度分别为(a) ε=0； (b) ε=0.016

第三类，无耦合时系统方向相是周期状态，有耦合后变成无序状态。图6展示ε=3.742时x的时间序列。很明显，弱耦合使得系统的方向相从周期五的相延迟同步状态，转变为无序状态。

参数为μ=3.742，耦合强度分别为(a) ε=0； (b) ε=0.013

3 结论

本文研究了弱耦合对二维耦合逻辑斯蒂映像格子系统的集体动力学行为的影响，基于方向相引入了序参量，用其刻画了系统方向相的状态，并对动力学分岔参数做了系统研究。研究结果表明，弱耦合对系统集体行为的影响非常复杂。首先，弱耦合的作用能够引起周期窗口消失。其次，弱耦合对无耦合时系统方向相处于无序状态的影响路径有两种：第一，随着耦合强度的增加，系统会先经历周期状态，再变为无序状态。第二，有了弱耦合的作用，系统方向相会直接从无序状态变为有序状态。最后，当系统无耦合处于周期状态时，弱耦合使系统集体动力学行为变为无序状态。值得一提的是，用本文的研究方法能够得到与Zhou Yin-zuo小组相同的结论。此外，本文只局限于一种网络拓扑结构，并未对同种网络拓扑结构的属性变化以及不同网络拓扑结构进行研究，这将是我们后续工作的研究方向。