基于层级深度强化学习的间歇控制算法

李广源，史海波，孙杳如

（同济大学电子与信息工程学院计算机科学与技术系，上海 201804）

0 引言

近年来，人工智能领域中出现了多种针对强化学习算法的测试平台，例如OpenAI的Universe、Gym、DeepMind 的 DeepMind Lab 等[1-2]。其中，MuJoCo通过模拟对仿真机器人的控制，搭建了针对高维、连续动作空间的强化学习测试平台[3]。由于在这些测试平台的仿真过程中，动作的执行不能获得即时的标签，因而动作策略的训练多采用如进化算法、强化学习等学习方法。近年来，由深度网络和强化学习结合的算法（深度强化学习）在连续动作空间问题中取得了接近人类水平的成绩，从而成为求解该类任务的研究热点[4-5]。

在连续动作空间任务中，如果能够得到任务环境的动力学方程就可能构建出高效的算法。例如在知道MuJoCo机械臂（Reacher）的动力学模型的前提下，Hall使用在线轨迹优化（Online Trajectory Optimization）算法规划机械臂的控制动作序列[6]。在没有进行离线训练的情况下，该算法能够实时高效的控制机械臂完成指定动作。然而，该算法需要事先确定任务环境的动力学模型，而大部分仿真环境具有较为复杂非线性动力学系统，其动力学方程难以使用解析式表达。

当仿真任务的环境支持离线的暂停和探索时，可以用蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）算法对决策进行探索。在可以使用Atari模拟器进行探索的前提下，利用MCTS算法对每一步决策进行搜索，最终在多数Atari游戏中取得超过人类水平的分数[7]。然而多数仿真环境以及真实世界中是不支持暂停和探索功能。

文献[6]中的算法利用了任务环境的先验知识，文献[7]中的算法需要仿真平台的特殊支持。为了提高算法的鲁棒性，Lillicrap等人在2016年提出了深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG），该算法实现了端到端、无模型的学习过程，并且在多种连续动作控制任务中表现出色。然而该方法在训练时收敛速度慢，同时在面对复杂的仿真环境时学习效果不稳定。

受到生物运动控制系统启发而提出了间歇控制（Intermittent Control，IC）[8,9]。间歇控制是一种具有层级结构的算法，其基本思想是将复杂的任务分解成具有层级结构的多个子任务，再针对每个子任务进行单独优化，从而实现高效的动作空间探索，提高算法的收敛速度[10]。在轨迹跟踪任务中，Wada等人提出了基于最小转换原则的曲线生成算法[11-12]，用以生成仿真的手写体字母。然而该算法中的目标点参数数量和位置是由人工调参得到，整个调参过程需要大量时间。

为了进一步提高算法的收敛时间，Schroecker提出了基于模仿学习的间歇控制算法。针对Reacher任务，该算法首先收集一批人工控制下得到的样本，在模型学习过程中，将动作的搜索空间限制在已有样本空间的附近，从而显著加快模型收敛的速度[13]。然而该算法最终效果和样本的质量相关性较大，当已有样本偏离最优解时，算法最终难以收敛到较好的水平。

针对具有连续动作空间和非线性动力学系统的仿真任务，为了提高算法的收敛速度和最终效果，以及实现无模型、高鲁棒性的策略学习，本文中融合间歇控制框架和DDPG算法提出了层级深度确定性策略梯度（Hierarchy Deep Deterministic Policy Gradient，HDDPG）模型。该模型由两个控制器组成，分别为高层控制器和低层控制器。高层控制器负责分解任务，将任务在时间上分解成多个离散的子任务。低层控制器负责完成具体的子任务执行，在每个时刻给出智能体（任务主体，例如在Reacher任务中，代理表示机械臂）需要执行的动作。其中低层控制器使用DDPG模型进行学习，实现了端到端，无模型的学习过程，避免了对任务环境的动力学模型的依赖和人工调参的过程。高层控制器同样使用DDPG模型，在模型学习的过程中，引入最小转换原则以启发模型找到最优的任务分解模式。最后在经典仿真任务轨迹跟踪（Tracking）和二连杆机械臂（Reacher）来验证算法。两个实验证明了HDDPG相对DDPG模型可以在更短的学习时间内找到最优解。

1 HDDPG算法

针对连续运动控制的层级控制模型HDDPG（Hier⁃archical Deep Deterministic Policy Gradient，HDDPG）。在HDDPG中，模型分为高层控制器和低层控制器，高层和低层控制器以两种不同粗细的时间粒度工作。高层控制器规划次级目标以及次级目标执行的时间。低层控制器在高层控制器规划的时间内执行与环境交互的动作，以期达到高层控制器规划的次级目标。高层控制器输出的次级目标和次级目标的执行时间是由连续的值表示，次级目标一般表示为环境中某个坐标。高层控制器和低层控制器都使用DDPG模型。

下面给出具体的算法描述：

低层控制器是一个典型的DDPG模型，在一个连续动作控制任务中，低层控制器环境的状态空间S，t时刻的环境状态st，其动作空间为A，时刻t的动作at，状态转移概率 p(st+1|st,at)，奖励函数r∈S×A。代理通过调整策略πθ的参数θ∈ℝn来最大化奖励函数。使用随机策略梯度法来更新参数θ。在每个时刻，环境的状态由上一个时刻环境的状态st-1和代理的动作at-1决定，同时，环境会给代理一个奖励r(st-1,at-1)。根据状态s，动作a和奖励r的序列{s1,a1,r1,…,sT,aT,rT} 来更新策略。每个时刻对应的累计奖励ℛ(s ,a)由公式决定，其中是γ衰减因子，取值范围为(0,1)，其中动作价值函数为Qπ(st,at)=E[ℛ(s ,a)|s=s1,a=a1,πθ]，价值函数为 Vt(st)=E[ℛ(s ,a)|s=st,πθ],模型学习的目标是最大化累计回报ℛ(s ,a)。使用梯度 ∇aQ(s ,a|θQ)来优化策略，其中Q是一个可微函数相应的，策略网络的梯度可以表示为使用Q-learning来更新动作价值函数，通过最小化δQ来优化动作价值网络，δQ是网络预测出的价值与累计回报之间的均方差。

DDPG算法在训练连续动作控制模型时往往需要较长的训练时间，且训练时间和难度随着任务自由度上升而变大，同时在针对复杂的运动控制任务时模型最终难以收敛。受到生物运动控制系统的层级结构的启发，我们将DDPG融入到间歇控制的框架中，即HD⁃DPG。HDDPG分为两层控制结构，每个控制结构均是由一个DDPG网络组成。高层控制器的目标是从宏观上分解整个任务，同时向低层控制器发出离散的命令，通过低层控制器间接与环境交互，从而完成整个控制任务。

相对于低层控制器，高层控制器在整个决策过程中的输出以更大的粒度表示。如图1所示，高层动作网络 μ(s|θμ)根据当前环境的状态信息输出次级目标gti∈S和低层控制器持续时间T(ti)。在代理执行任务的时候，低层控制器接受高层控制器输出的间歇目标gti和持续时间T(ti)，由低层控制器去生成与环境交互的动作ak，并且执行持续时间T(ti)，代理得到新环境这段时间的累计回报由环境在时间T(ti)内的累计回报。高层控制器的目标是最大化整个间歇控制过程中的累计回报高层控制器中价值网络E[Fti|μθμ]是环境和高层控制器的动作决定(gti,,Tti)的。动作网络的学习策略是

评价网络的学习策略是最小化评价网络δQ根据当前状态s和动作a预测出的q和累计回报之间的均方差。是环境在时间Ti内的累积回报。高层控制器根据来自环境的累积回报 fti进行学习。低层控制器根据 fti进行学习。是下一个关键点的预测动作价值

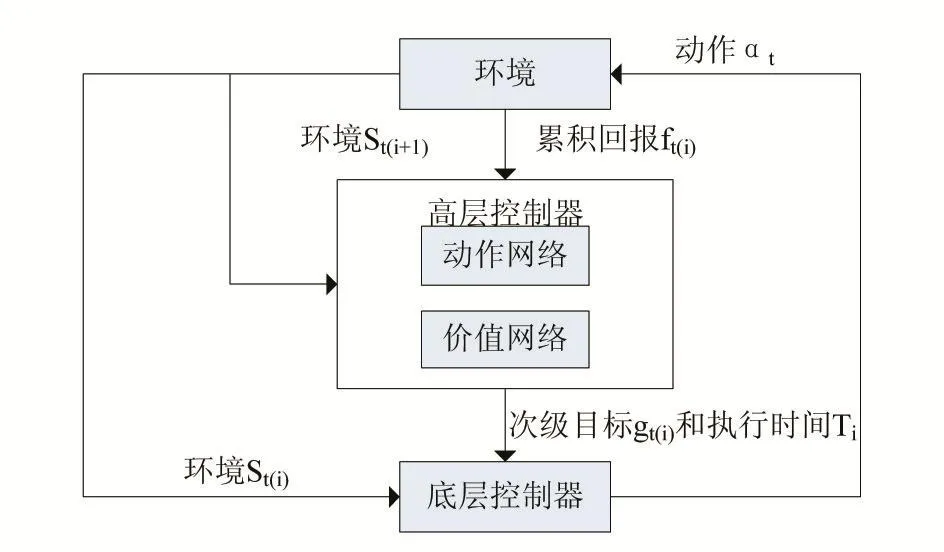
图1 HDDPG的层级架构

2 实验设计

为了验证HDDPG模型能够有效地完成连续动作控制任务，我们使用了两个虚拟任务来验证模型的效果。第一个任务是轨迹跟踪任务轨迹跟踪（Puck World）。Puck World是一个虚拟的二维矩形平面，以其中心为原点，x和y轴的范围均为[- 1,1]，假设平面上存在一质点，并且该质点与平面之间存在摩擦力，轨迹跟踪任务指在规定时间内通过给出作用于质点在x和y轴方向的力，使得质点从起点到终点所走过的路径符合预期的轨迹。其中环境(xt,yt)分别为质点在t时刻的坐标，(vt,ut)为质点在t时刻在x和y轴方向的分速度，(x′,y′) 为终点所在的坐标，(v′,u′)为终点在x和y轴方向的分速度。作用于质点的动作at=( ft,gt),( ft,gt)分别为t时刻作用于质点x和y轴方向的力。

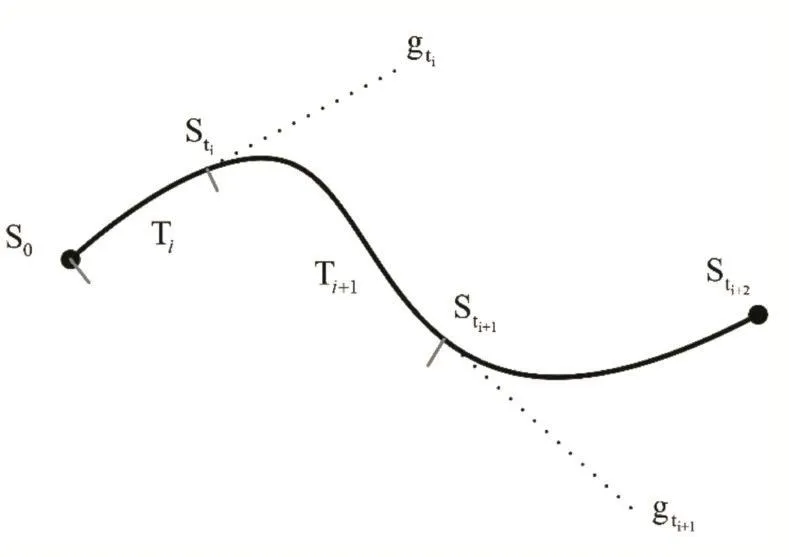
图2 连续动作控制任务在时间上分解的示意图

如图2所示在轨迹跟踪任务中，低层控制器直接与环境交互(质点)，低层控制器的环境 sit=(xt,yt,vt,ut,xi,yi,vi,ui),其中(xi,yi,vi,ui)为高层控制器给出的第i个间歇目标点，Ti为高层控制器给出的第i个执行时间，在时间Ti中低层控制器每个时刻t都给出一个动作at=( ft,gt)直接作用于质点。高层控制器的环境高层控制器给出的动作ai=(xi,yi,vi,ui,Ti)。

HDDPG的学习过程分为两个阶段，第一个阶段是低层控制器的学习，第二阶段是高层控制器的学习。低层控制器的学习是一个典型的DDPG学习过程。其中环境s=(x ,y,v,u,x′,y′,v′,u′) ，每次采集样本都是随机生成一个新的s，每次迭代固定步数为40。低层控制器的每步奖励函数为

3 结果分析

模型最终学会控制低层控制器去跟踪这些轨迹。图11展示了HDDPG和DDPG在轨迹跟踪任务中的累积奖励随着训练时间的变化。DDPG模型收敛于一个较低的累积奖励值并且具有较大的波动，而HDDPG则能较快的收敛于一个很高的累积奖励值，同时具有较好的稳定性。x轴是训练时间，单位是小时，y轴是累积奖励。这里累积奖励是10个HDDPG和10个DDPG模型的累积奖励的平均值。

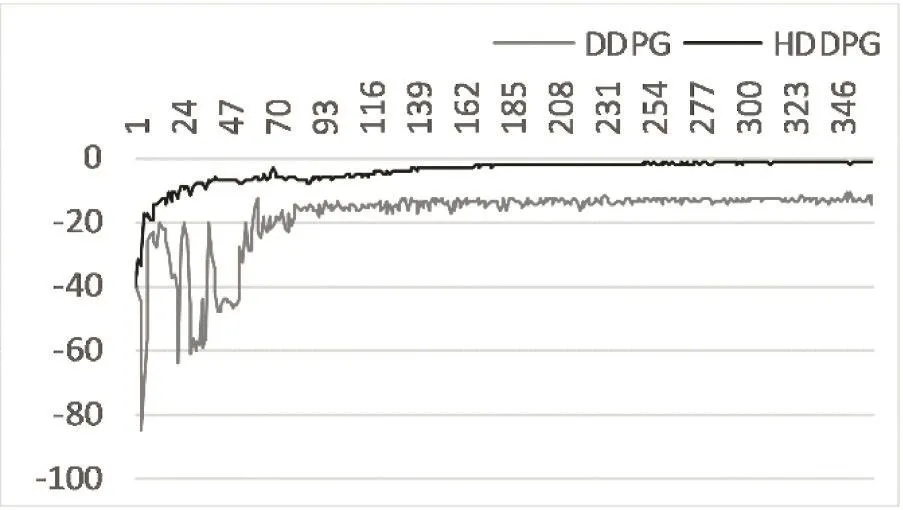
图3 DDPG与HDDPG在轨迹跟踪任务学习过程中累计奖励变化

图4描述了HDDPG模型与DDPG模型在轨迹跟踪任务中最终位置与目标点的距离。从图中可以看到，在DDPG模型中，7个模型不能收敛，3个收敛的模型也没有到达终点附近（距离终点欧氏距离0.1以内算作到达附近）。在HDDPG中，最终有6个模型能够到达终点附近，剩下4个模型进行了无效的探索。值得注意的是，如果在运行过程碰到环境范围边界，则本回合直接结束。

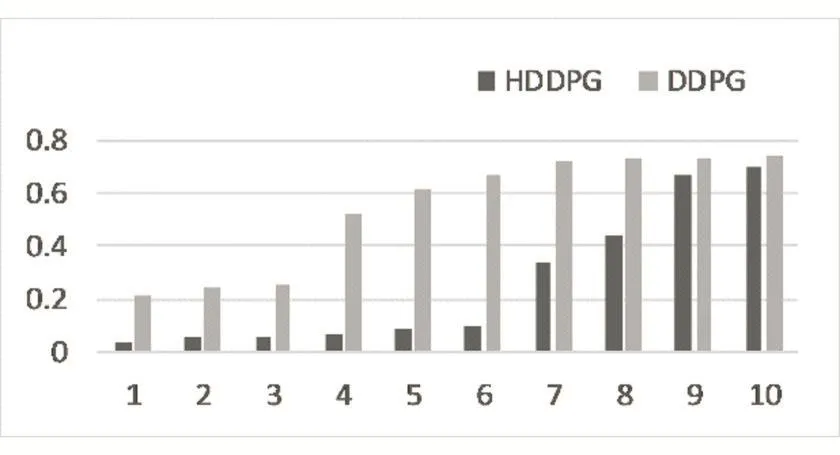
图4 DDPG与HDDPG任务完成时末端与终点距离

4 结语

HDDPG与普通DDPG相比，在连续控制任务中具有更快的收敛速度和更好的效果。其原因可归于两点，第一点是HDDPG直接在高层空间进行探索。高层控制器输出的是低层控制器的间歇目标和持续时间，其中微小的变化可以导致最终轨迹出现较大的不同，具有更高的探索效率，有利于模型快速的探索环境信息。这一点和遗传算法中的间接编码有些类似。同时高层控制器模型的值函数的复杂程度随着层级的提高而提高，将值函数以层级的结构表示有助于学习得到更准确的值函数，从而进一步提升复杂运动控制的性能。

第二点在学习过程中，估值网络通过时间差分从后往前的迭代来逼近正确的值函数。如果动作序列较长，则迭代的次数较多，所需的计算资源也较多，训练所需时间长。而对于高层控制器的估值网络来说，只需产生个位数的间歇控制动作，具有较短的动作序列，减少了计算所需资源。