仅地心矢量测量的卫星转对地定向姿态控制方法*

2019-01-22雷拥军魏春岭何英姿

空间控制技术与应用 2018年6期

雷拥军，魏春岭，何英姿，刘洁

0 引言

具有智能自主控制能力的航天器具备轨道与姿态的自主控制能力，特别是高级智能自主控制具有对付一定范围的不确定性事件的智能控制能力[1]，一般需要强大的知识库与有力的控制策略作为支撑.航天器在轨异常后自主生存及系统功能自主恢复等均是智能自主控制亟待解决的重大问题之一.

当航天器在轨异常现象可能最初由星上个别设备或部件故障触发.文献[2]对1975-2007年期间272次在轨卫星故障统计得出57%失效会影响控制和电源分系统，37%故障源于控制分系统且其中一半又源于陀螺、动量轮与推力器.一旦系统异常发生后可能因工作条件发生较大改变而使得星上大部分部件无法适应，如星体速度过大导致敏感器测量或执行机构力矩输出等问题使得姿态失去控制能力[3-5]，从而给航天器生存及系统功能恢复带来巨大挑战.在姿态测量信息不完备情况下，通过最小敏感器配置测量及时获取星上姿态相关信息对在轨应急处置措施制定及实施显得尤为重要,如已有在轨卫星姿态异常后采用了基于0-1式太阳敏感器、磁强计、数字太阳敏感器或红外地平仪等的系统自旋角速度确定[3,5-7]以及遥测异常中断后采用的基于射频RF的星体自旋角速度确定[8]技术等.

以尽量少的部件配置实现高可靠系统一直是航天器控制工程设计的一大目标，不依赖于三轴完备姿态测量及控制的偏置动量控制技术得到广泛应用[9-11]，但该方法基于轨道罗盘效应与近似线性化系统设计，无法适应姿态角及角速度过大使得系统具有多轴耦合强非线性特性场合应用.针对在轨姿态恢复问题，目前大量文献进行了三轴姿态均可测前提下的执行机构欠驱动控制方法研究[12-14]及小卫星磁控姿态捕获技术研究[15-17]，但对敏感器测量信息匮乏下如何使得卫星自主恢复对地姿态的研究甚少.

基于零动量控制的高精度对地遥感卫星[18-21]除配置星敏感器与陀螺高精度姿态敏感器外，通常还配备基于地心矢量及太阳矢量测量的大视场高可靠一般精度敏感器以提高系统可靠性，并考虑姿态异常后基于星体对日定向安全模式设计以确保整星电源安全.然而当姿态异常伴随星体大角速度使得陀螺饱和，特别如文献[3]中姿态异常本身就由陀螺故障导致时，将缺乏有效角速度测量而难以按已有安全模式设计自主实现对日定向，一旦异常未能及时处置则可能进一步引发电源安全及推进剂冰冻等问题，给后续处置带来极大困难.对于在轨异常角速度过大的姿态恢复问题，文献[3-5]由地面通过地球敏感器或太阳敏感器测量获悉星上状态，并制定两步骤解决措施：首先，制定并实施星体消旋及进动控制策略以保证整星结构及电源安全；然后，结合卫星及环境特性分析实施由日状态下的对地姿态捕获及恢复控制策略.上述整个过程可能持续达数月，需消耗了大量人力及物力[3-4].

针对上述系统异常下敏感器测量信息匮乏的姿态快速自主恢复问题，本文设计了一种仅依赖地心矢量测量信息的天平角抑制与能耗速率阻尼相结合的星体异常姿态转正常对地姿态的控制器，引入星体角动量偏置技术手段使得随旋转能量耗散的同时星体趋于三轴稳定对地姿态，可解决在无角速度测量下的异常姿态快速自主恢复问题，通过数学仿真验证了方法的有效性.

1 问题描述

(1)

式中，ωbo为星体相对轨道系的角速度.

采用非角动量交换装置执行机构的星体动力学方程为

(2)

式中，J为星体惯量阵，且JT=J>0；ω为星体惯性角速度；τ为作用于星体的控制力矩.

记ωo=[0 -ωo0]T为轨道角速度(ωo>0)，有如下关系：

ω=ωbo+CBOωo

(3)

式中，CBO星体系相对轨道系的方向余弦阵，其与q的关系为

当已知星体滚动角φ、俯仰角θ和偏航角ψ时，可以选定的欧拉转序计算得到CBO,以3-2-1欧拉转序姿态描述的卫星本体系相对轨道坐标系的方向余弦阵为

其中：s(·)、c(·)分别表示相应姿态角的正弦与余弦.

在卫星稳定对地时，基于姿态与角速度测量反馈控制方式可实现三轴姿态控制，并使得

q→[0 0 0 1]T或[φθψ]T→0

及

ωbo→[000]T或ω→ωo

当卫星在轨系统异常且角速度过大，出现仅地球敏感器测量输出有效而其它敏感器测量失效，在无法获取如文献[21]所示常规三轴姿态控制所需完备姿态信息及角速度测量信息时，如何实现无角速度测量下仅利用地心矢量信息实现卫星从任意姿态失控状态快速自主恢复三轴对地稳定运行状态为本文待解决问题.

2 基于天平角及能耗的姿态控制

由卫星质心指向地心的单位矢量即为地心矢量，其在星体下表示为EB为

(4)

其可由地球敏感器测量得到，在三轴稳定对地零姿态下地心矢量EB与沿星体zB轴的单位矢量zB=[0 0 1]T重合.

向量EB、zB间夹角可作为衡量星体姿态偏差参量之一，故定义其为天平角ϑ，即

(5)

定义天平角矢量在星体坐标系下的表示Vϑ为

(6)

当沿Vϑ方向在星体上施加控制力矩时，可对天平角ϑ进行控制.为提高系统动态特性，需在控制中引入星体角速度相关信息.如图1所示，星体相对轨道坐标系以角速度ωbo转动，地心矢量沿轨道坐标系轴zo方向且在轨道坐标系o-xoyozo下相对静止，向量EB相对星体系o-xByBzB具有相对运动，若星体偏离对地零姿态往返运动时则地心矢量如同空间天平摆在星体下做相应摆动.

图1 地心矢量在星体下运动示意图Fig.1 Schematic representation for the motion of geocentric vector in the satellite body frame

星体相对轨道坐标系角速度ωbo可分解为沿EB方向分量ωboE与沿其垂直方向分量ωboE⊥两部分，由于EB为单位向量，于是有

从而当沿ωboE⊥反方向对星体施加阻尼力矩可耗散星体关于ωboE⊥的相关动能.

结合天平角抑制与依据地心矢量测量变化趋势能量耗散速率阻尼的综合控制律为

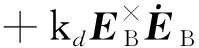
(7)

式中：控制参数kϑ、kd>0.

对EB求时间导数，有

(8)

将式(8)代入式(7)，有

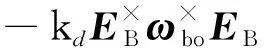
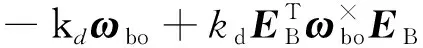
(9)

上述第二等式的第二项反映了式(7)所具有的速率阻尼作用.

在天平角抑制控制及能耗控制下向量EB将与zB重合，此时星体zB轴指向地心，但是由于与星体角速度沿EB的分量ωboE相关动能无法通过施加阻尼力矩方式来耗散掉，因此星体仍无法实现期望的三轴对地稳定姿态.为克服上述问题，可在星体-yB方向引入角动量偏置策略，从而使得角速度ωbo被阻尼至零之前由于轨道运动与星体偏置角动量耦合的陀螺力矩使得向量EB无法与zB维持重合状态.

在-yB方向角动量偏置的卫星动力学为

(10)

式中：Hbias=[0 -Hbias0]T为偏置角动量，且Hbias>0.

不妨假设卫星运行于圆轨道或小偏心率轨道，于是ωo可看作为常数，对式(3)两边求时间导数为

(11)

利用式(9)与式(10)，式(8)可写为

(CBOωo)×JCBOωo-(CBOωo)×Hbias+τ

(12)

星体转动惯量的惯量积一般为小量，忽略其影响有

(CBOωo)×JCBOωo=0

于是式(12)可写为

(13)

3 系统平衡点及其特性分析

式(1)与式(13)所示原对象系统在式(7)控制作用下组成的闭环系统具有强非线性特性，与线性系统区别是可能存在多平衡点问题[22]，故其所有平衡点获知及其特性分析对实际系统控制设计尤为重要，乃至需采取必要手段以规避系统状态轨迹稳定维持在非期望平衡状态.

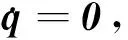
-(CBOωo)×Hbias+τ=0

(14)

利用式(7)，式(13)可写为

(CBOωo)×Hbias+kϑVϑ=0

(15)

上式几何意义为向量(CBOωo)×Hbias与Vϑ的线性组合为零.考虑向量(CBOωo)×Hbias垂直星体yB轴及Vϑ垂直星体zB轴，为使得式(15)成立的平衡点姿态参数有如下两种情况：

(1) (CBOωo)×Hbias与Vϑ均为非零向量.

由式(15)有(CBOωo)×Hbias与Vϑ平行，考虑(CBOωo)×Hbias垂直星体zB轴且Vϑ垂直于星体zB轴，故(CBOωo)×Hbias与Vϑ均必平行于星体xB轴，从而CBOωo与EB势必在星体yBozB平面内.

式(15)可表示为

HBias(CBOωo)×yB+kϑVϑ=0

其中yB=[0 1 0]T

考虑地心矢量与轨道法线矢量垂直关系，即向量EB与CBOωo正交，上式等式成立的必要条件为

kϑ=HBiasωo

(16)

因此，当选取控制参数kϑ及偏置角动量幅值Hbias使得式(16)不成立时，则(CBOωo)×Hbias与Vϑ为非零向量时系统不存在平衡点.

(2) (CBOωo)×Hbias与Vϑ均为零向量.

在该条件下，CBOωo平行于星体yB轴且EB平行于星体zB轴.由偏置角动量Hbias表达式可知，CBOωo平行于星体yB轴且EB平行于星体zB轴时，故(CBOωo)×Hbias与Vϑ均为零向量，对应姿态有如下几种可能性：

(a) 星体yB、zB轴分别沿轨道系yo轴与EB方向，此时星体坐标系与轨道坐标系重合，对应方向余弦阵CBO(qe)为单位阵且平衡点对应的姿态参数为qe=[0 0 0 1]T.

在此平衡点附近，利用式(4)、(6)，且略去二阶小量后控制律式(9)可近似表示为

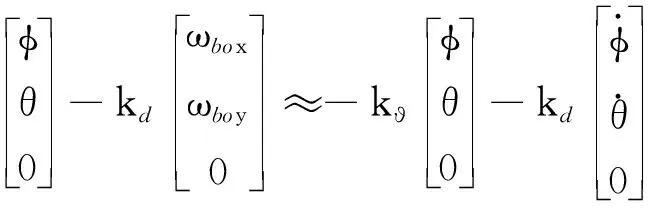
该表达式即为常规偏置角动量控制形式[9]，从而可知闭环系统在上述姿态参数下的平衡点是稳定的.

(b) 星体yB与轨道系yo轴重合且EB沿zB轴反向，对应方向余弦阵为

且平衡状态中姿态参数为qe=[0 1 0 0]T.

在该平衡点附近，由偏置角动量在轨道角速度下产生的陀螺力矩使得星体yB趋向轨道系yo轴，但在控制力矩中的kϑVϑ项产生EB偏离星体-zB轴的作用，故该平衡点是不稳定的.

与

且平衡点的对应姿态参数分别为

qe=[0 0 1 0]T与qe=[1 0 0 0]T

上述两种情况下，由于偏置角动量与轨道坐标系yo轴而非其负向方向，偏置动量产生的陀螺力矩使得系统偏离平衡状态呈现不稳定特性.

综上系统平衡点求解及其特性分析，在合理选取控制参数及偏置角动量幅值下由式(1)、式(13)与式(7)组成的非线性系统存在4个平衡点，其中仅有期望的三轴对地稳定姿态所对应的平衡点

{(ωbo,e,qe)|ωbo,e=0,qe=[0 0 0 1]T}

为闭环系统的稳定平衡点.

4 数学仿真校验

以运行于轨道高度为500 km的对地稳定卫星为例，对应轨道角速率为ωo=[0 -0.0634 0]T((°)/s)，对应轨道周期约5 680 s，星体转动惯量为

J=diag{640, 560, 480}(kg·m2)

星体偏置角动量设置为

Hbias=[0 -35 0]T(N·m·s)

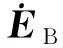
仿真中取Ts=0.5 s.

星体初始角速度为ω=[2-1-2]T(°)/s，对地三轴欧拉姿态为φ=60°、θ=120°与ψ=-30°，选取控制参数为kϑ=0.01、kd=50，对应的仿真结果如图2～图4所示.从图2与图3可知，实现星体角速率有效阻尼，星体对地三轴欧拉姿态角趋于零且星体惯性角速度趋近于ωo，约2 000 s时间成功实现三轴对地稳定运行；从图4可知在此控制过程中星体动能持续衰减.

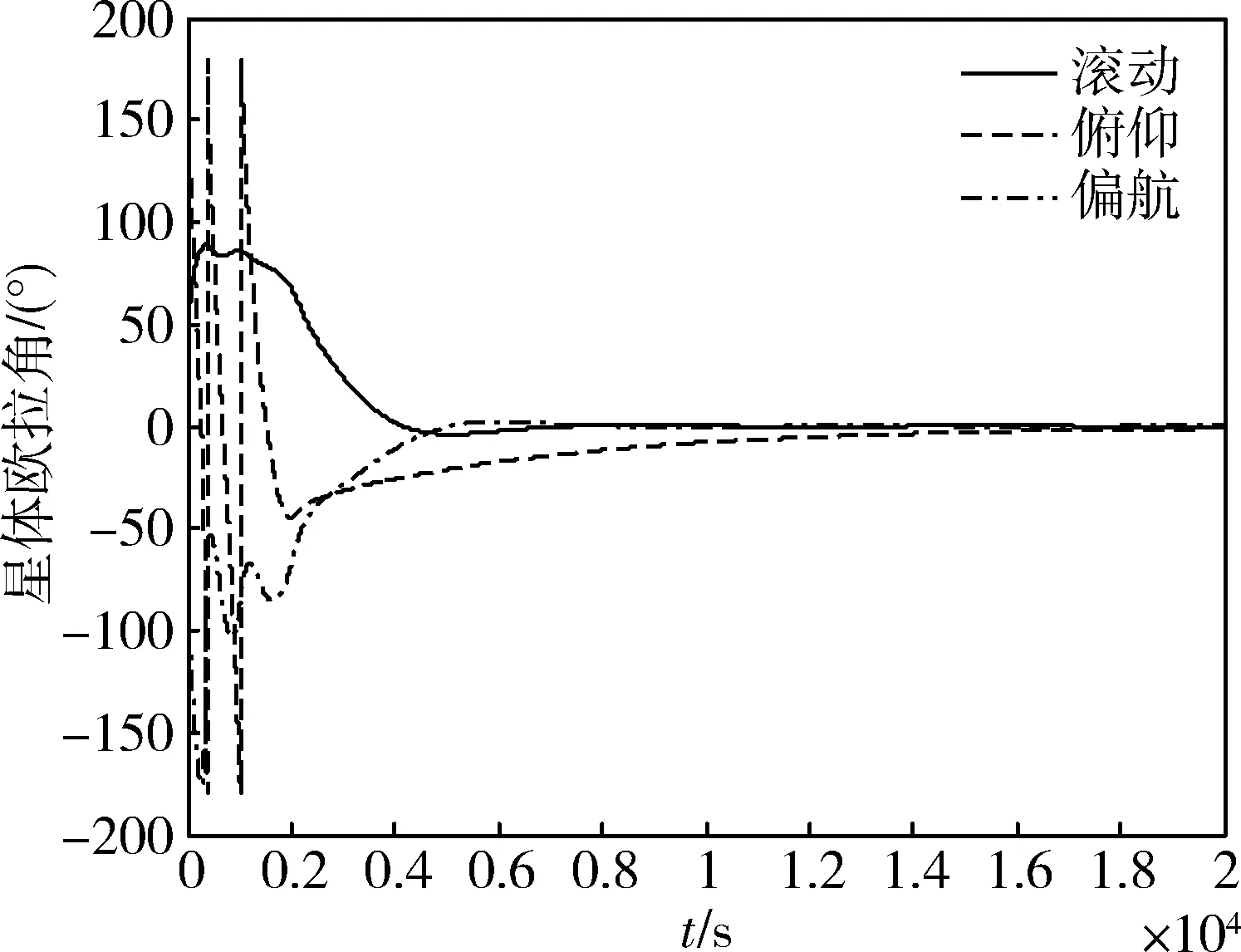
图2 欧拉姿态角Fig.2 Euler angles of satellite

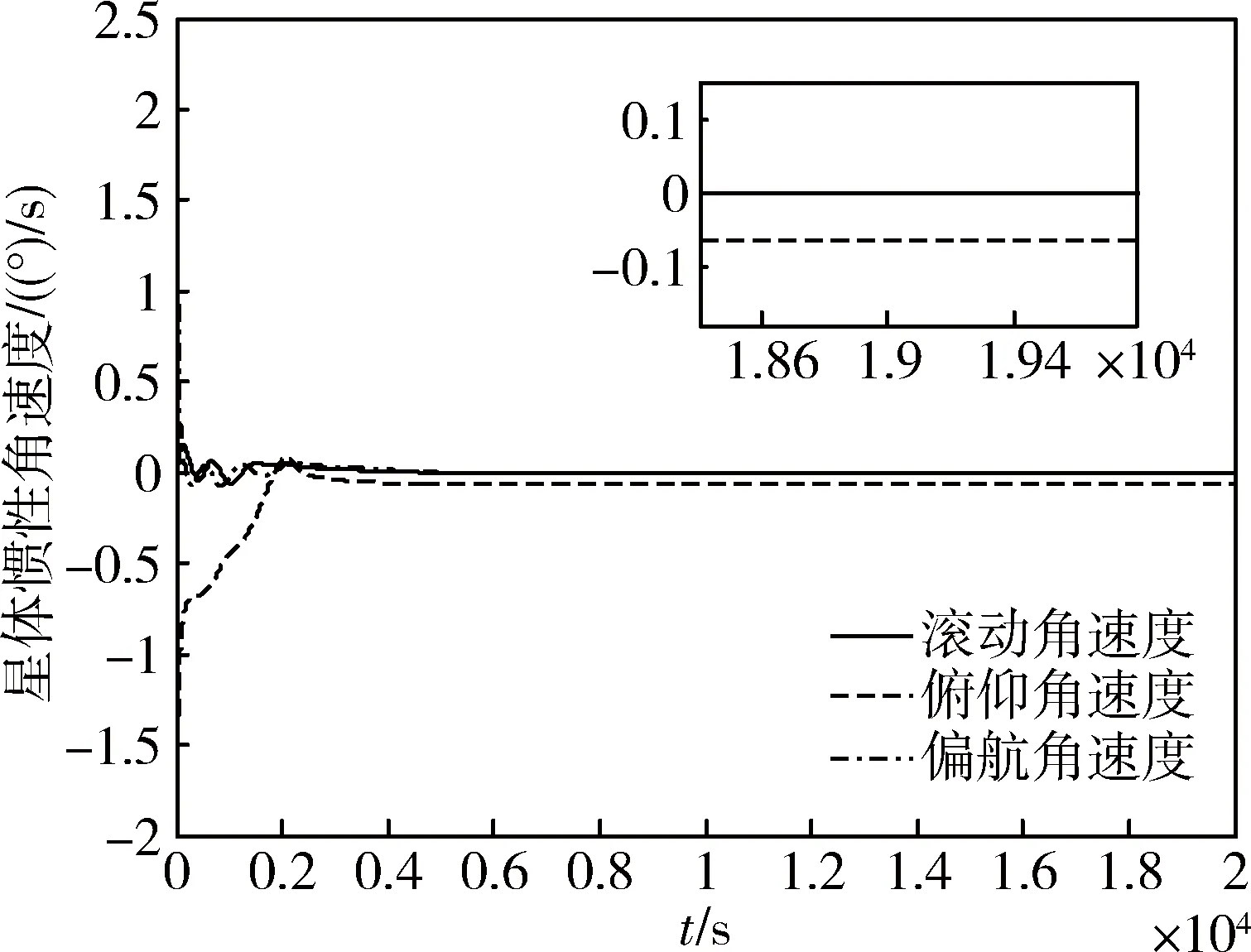
图3 姿态角速度Fig.3 Angular rates of satellite

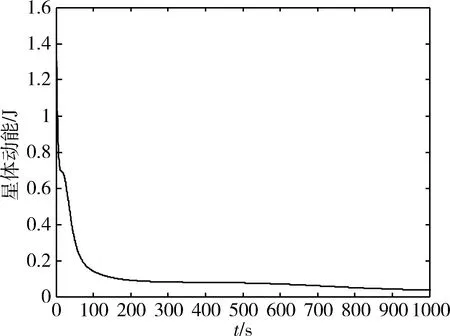
图4 星体旋转动能Fig.4 Kinetic energy of satellite

针对系统不稳定平衡点

{(ωbo,e,qe)|ωbo,e=0,qe=[1 0 0 0]T}

对应对地三轴欧拉姿态φ=180°、θ=0°与ψ=0°，此时地心矢量沿星体-zB轴且轨道角速度矢量沿星体yB，系统初始状态为

{(ω,q)|ω=[0 0.06 0]T(°)/s,

q=[1 0 0 0]T}

采用控制参数kϑ=0.01、kd=50，仿真结果图5与图6分别给出了地心矢量在星体下运动规律及星体角速度，由此可知在约22 000 s运动临近另外一个不稳定平衡点

{(ωbo,e,qe)|ωbo,e=0,qe=[0 1 0 0]T}

此时地心矢量在星体xB轴分量EBx接近于1且在其它两轴分量EBy与EBz均接近于零，轨道角速度矢量近似平行于星体yB轴，此后星体运动脱离该非稳定平衡点，约45 000 s在偏离上述不稳定平衡点后姿态迅速调整使得轨道角速度矢量及地心矢量分别趋近平行于星体-yB与zB轴，实现期望的对地稳定运行.

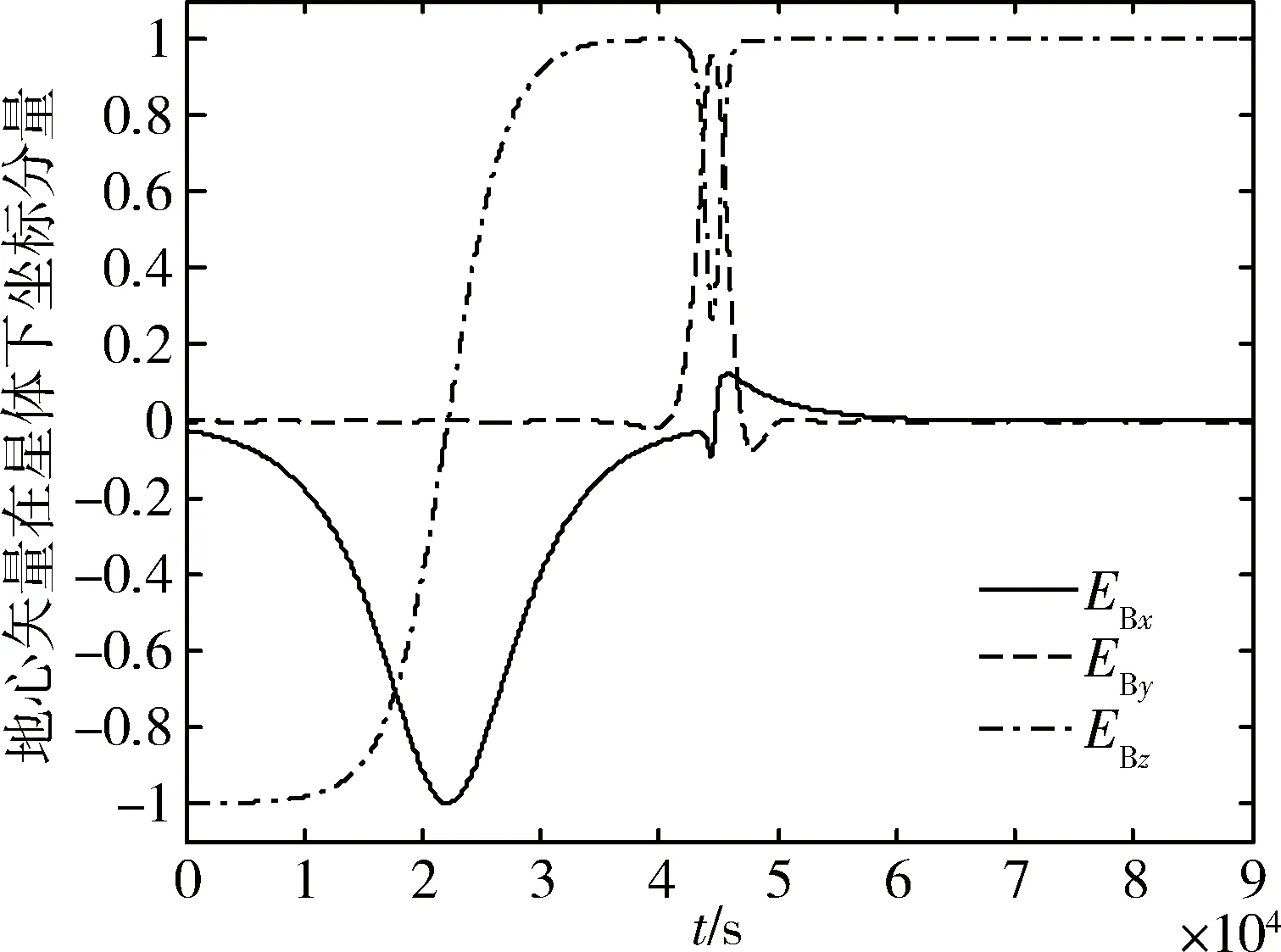
图5 地心矢量在星本体下坐标Fig.5 Geocentric vector coordinates inthe satellite body frame

图6 姿态角速度Fig.6 Angular rates of satellite

针对上述地心矢量沿星体-zB轴的不稳定平衡状态，由式(6)所示Vϑ形式可知式(7)中天平角控制量过小时系统脱离不稳定平衡状态时间略长.当控制参数选取为kϑ=0.5、kd=50时，维持上述仿真其他条件下得到的仿真结果如7与图8所示.由图7可知，在不到1 000 s时间内星体+zB轴转动180°由背离地心方向转动到指向地心方向，结合图8可知该状态为星体+yB轴沿轨道法线方向的不稳定平衡状态的对地姿态，并在10 000 s时间内脱离该平衡平稳点快速地转入正常对地稳定运行状态.