滚动轴承的材料显微实验和接触强度分析

王琳琳

(安徽冶金科技职业学院，安徽 马鞍山 243000)

滚动轴承是轴及其他旋转构件的重要支承。由于其使用过程中的维护极为方便，支承构造简单，容易装卸，因此，滚动轴承应用领域极为广泛并且已逐步将滑动轴承的位置取代。受到重载荷作用下的轴承，在工作过程中，因为尺寸较大，滚动体与内外套圈的接触变形加大，滚动体的接触状态复杂，失效分析也较复杂[1-2]。在一些发达国家，针对滚动轴承常规设计的要求、制造技术和选型方法等做出了更为详细的研究，制订了采用现代设计技术的设计规范、实现了系统性控形制造技术等，拥有高稳定性的高速度、重载滚动轴承的设计与制造，为一些动力装备提供了安全稳定可靠的流动轴承，例如：燃气轮机、发电机组、航空发动机组等。[3-5]高速过程中的滚动轴承长时间处于高压状态，由于工况条件恶劣，滚动轴承的内部元件在接触过程中会产生较大的应力，极易引起轴承的点烛失效，轴承寿命判断的依据便是点烛失效，因而对高速运转过程中的滚动轴承的元件之间接触强度的分析和疲劳计算具有重要意义。[6]

本文针对某企业进口滚动轴承，对其材料成分进行扫描电镜分析，同时利用ANSYS软件对滚动轴承进行有限元接触强度分析和疲劳计算。

1 滚动轴承的材料显微成分实验分析

该轴承是某企业从国外进口的，要在较高的接触应力下和转速下运行。其结构如图1所示，主要包括内圈、外圈和滚柱。主要尺寸：外圈直径1 960 mm，高1 200 mm，内环直径1 700 mm。内圈直径1 400 mm，760 mm，内环直径1 200 mm。滚子直径180 mm，高730 mm。

图1 滚动轴承装配图

为保证该滚动轴承有较高强度和较长使用寿命，要求其有较高的抗疲劳强度，[7]本文通过取样和显微实验，在扫描电镜下观察和分析滚动轴承各部件(内圈、外圈、滚柱)的材料组成元素及成分值。

1.1 滚柱的材料显微成分

表1可知，滚柱的主要元素为Fe、Mn、Cr，其中又以Fe的含量最多。Fe原子占有百分比是97.35，能量谱Fe的峰值也最高。

表1 滚柱的元素成分及含量

1.2 外圈的材料显微成分

由表2可知，外圈元素含量以Fe元素最多，Mn元素次之，Cr元素最少，能谱图也是如此。

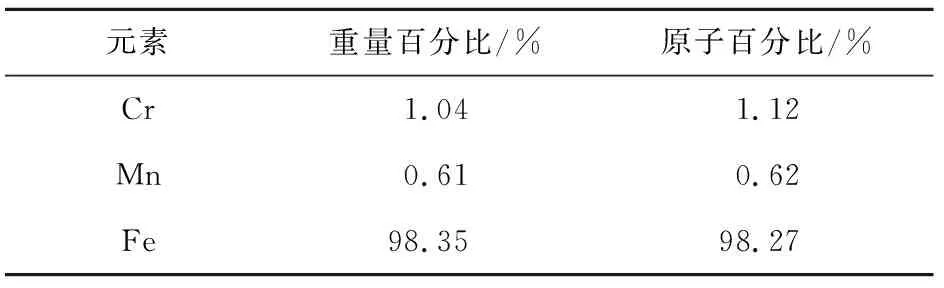
表2 外圈的元素成分及含量

1.3 内圈的材料显微成分

由表3可以看出内圈元素含量多少依次为Fe、Mn、Cr、Si，而且它们的重量百分比与原子百分比相差不大。

表3 内圈的元素成分及含量

通过以上扫描电镜观察和分析，根据该轴承的材料成分组成，查阅材料手册并取相近的值，得到该轴承的材料属性：弹性模量为2.1×105MPa，泊松比为0.3，摩擦系数为0.005。

2 滚动轴承的接触强度分析

2.1 接触问题的有限元法

由两个接触物体组成系统后，依据变分原理，与接触边界相关的单元e上，其外力虚功为

(1)

(2)

式中：δe为单元内的应力向量，是坐标的函数；δεe为单元内的虚应变向量；Ωe为单元区域；Γ为单元面力的边界。

由弹性力学的虚功原理可以知道，当系统处于平衡状态的时候，其外力功和内力虚功相等，即

(3)

由于{δue}的任意性，可以导出接触有限元分析的基本控制方程为：

(4)

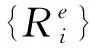
2.2 接触分析的有限元模型

整个滚动轴承中共有24个圆柱滚子，考虑模型的对称性和计算成本，建立1/24几何模型，分析径向载荷作用下轴承的滚子与内、外套圈之间的接触强度与变形规律。

根据上节的显微实验分析结果定义，或输入轴承的材料属性和实常数，并采用solid 45单元类型对几何实体模型划分网格。

2.3 接触对的创建

当程序进行是否接触的检查时，接触对外法线方向非常重要的。对3D单元，按节点序号以右手法则来决定单元的外法向，接触面的外法向应指向目标面，否则，在开始分析计算时，程序可能会认为有面的过度渗透，此时程序一般会立即停止执行。

本文采用Contact 3D targe 170模拟与内、外套圈接触的圆柱滚子的外表面，采用Contact 3D targe 174模拟与圆柱滚子外表面接触的内、外套圈的内表面。

2.4 接触强度计算结果及分析

通过有限元求解后，在后处理模块中可获取所需的应力和变形等计算结果。

2.4.1 接触应力分布云图

从图2～3中可以看出，最大接触应力发生在滚动轴承内圈，且最大接触应力为18 MPa，且最大应力发生在轴承的两端。

图2 内圈接触对的接触应力

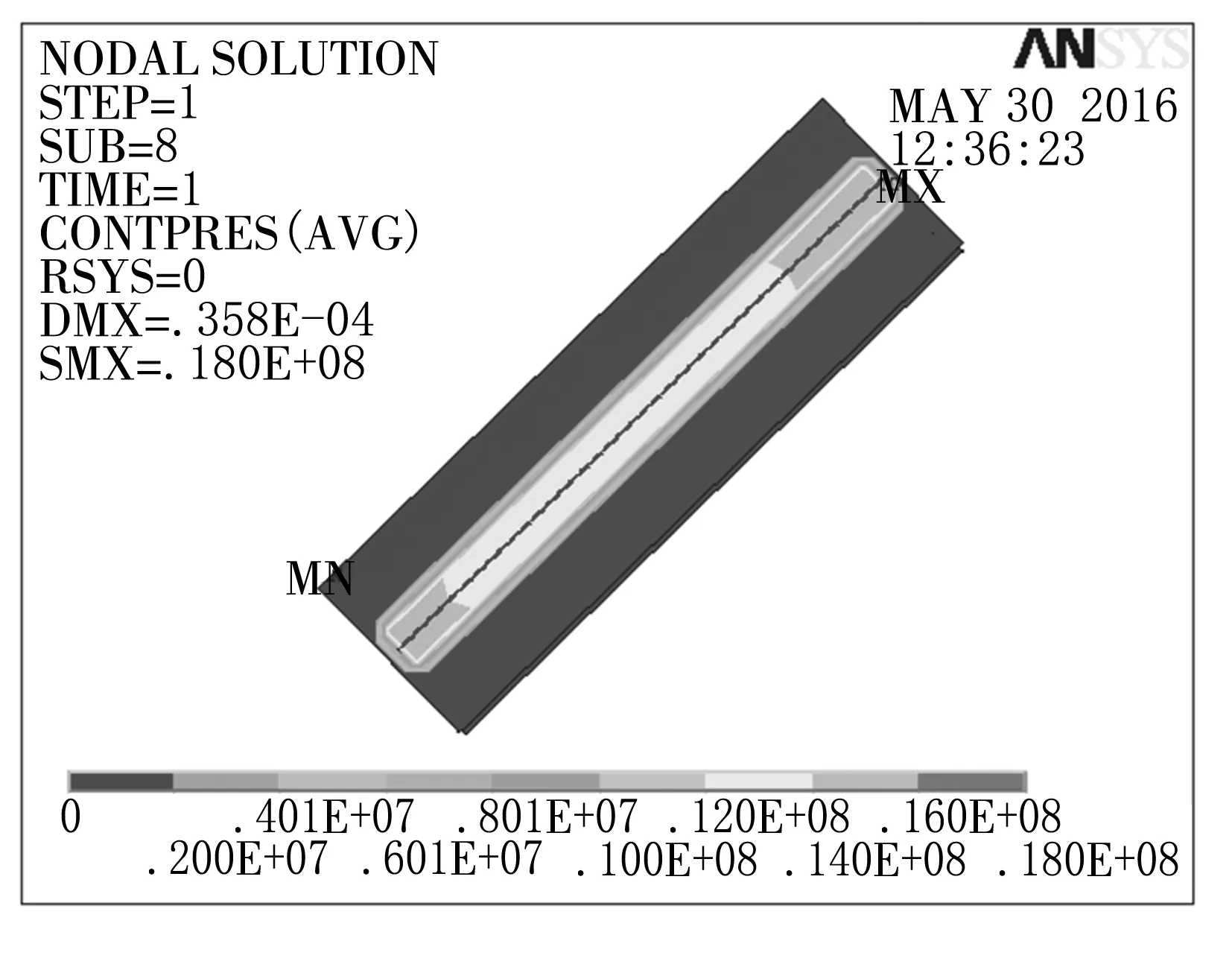
图3 外圈接触对的接触应力

从图4～6中可知，滚柱最大应力为2.64×107MPa，且发生在与内圈接触的那一侧，内圈最大应力为2.27×108MPa，外圈最大应力为9.7×106MPa，因此轴承在运行时最容易损坏的是内圈。

图4 滚柱Mises应力

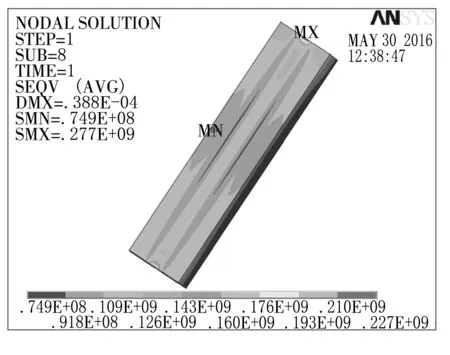
图5 内圈Mises应力

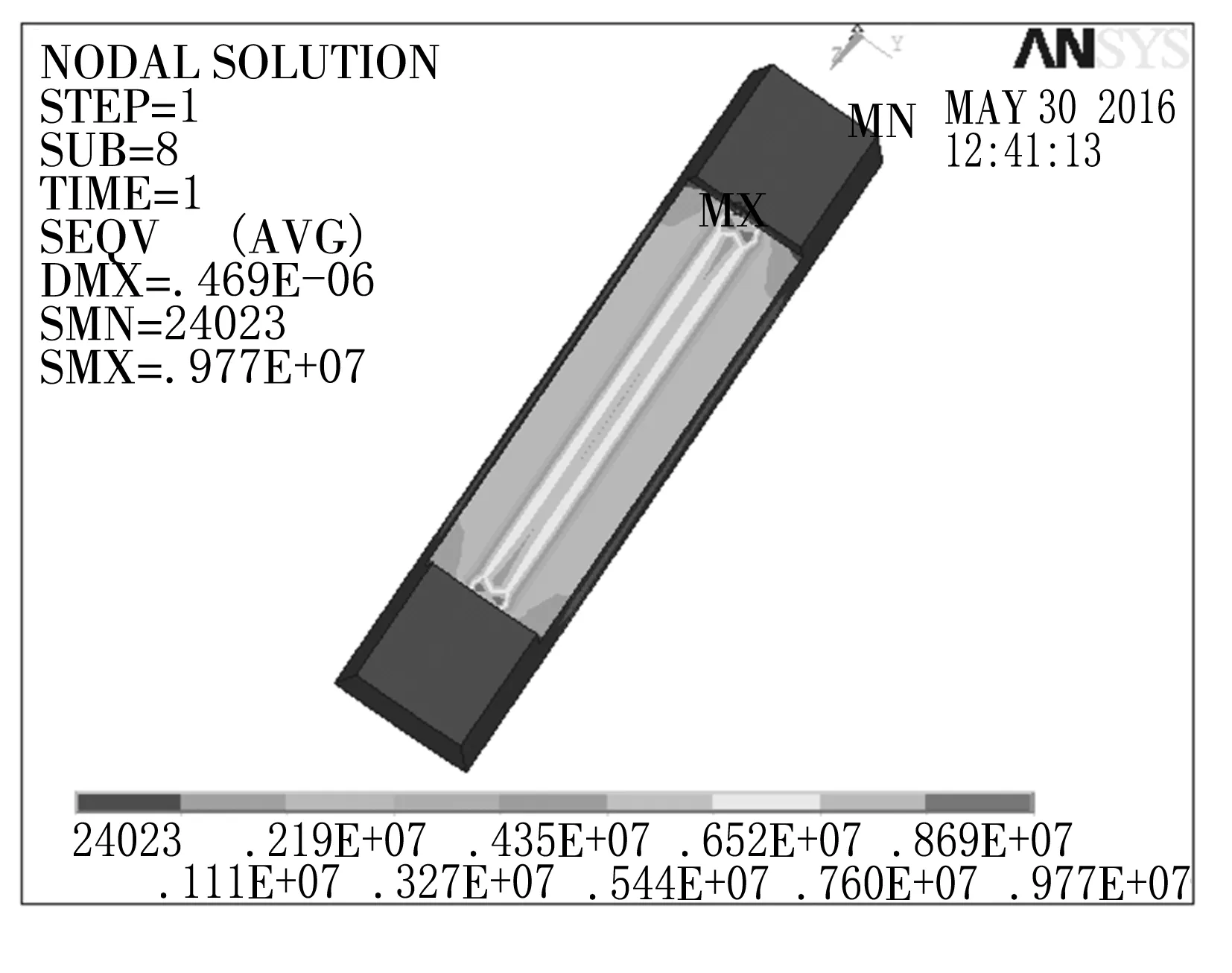
图6 外圈Mises应力

2.4.2 接触渗透量分布云图

从图7～8中可知，内圈与滚柱的渗透量是0.016 9 mm，且发生在接触的两端。外圈与滚柱的渗透量是0.16 mm，发生在接触对的下端。

图7 内圈接触对的渗透量

2.4.3 变形分布云图

从图9～11中可以看出，内圈的最大变形为0.038 3 mm，滚柱的最大变形为0.016 5 mm，外圈的最大变形为0.006 9 mm。整个模型的变形都在允许范围内，其中滚柱的变形与前面的接触渗透量相近。

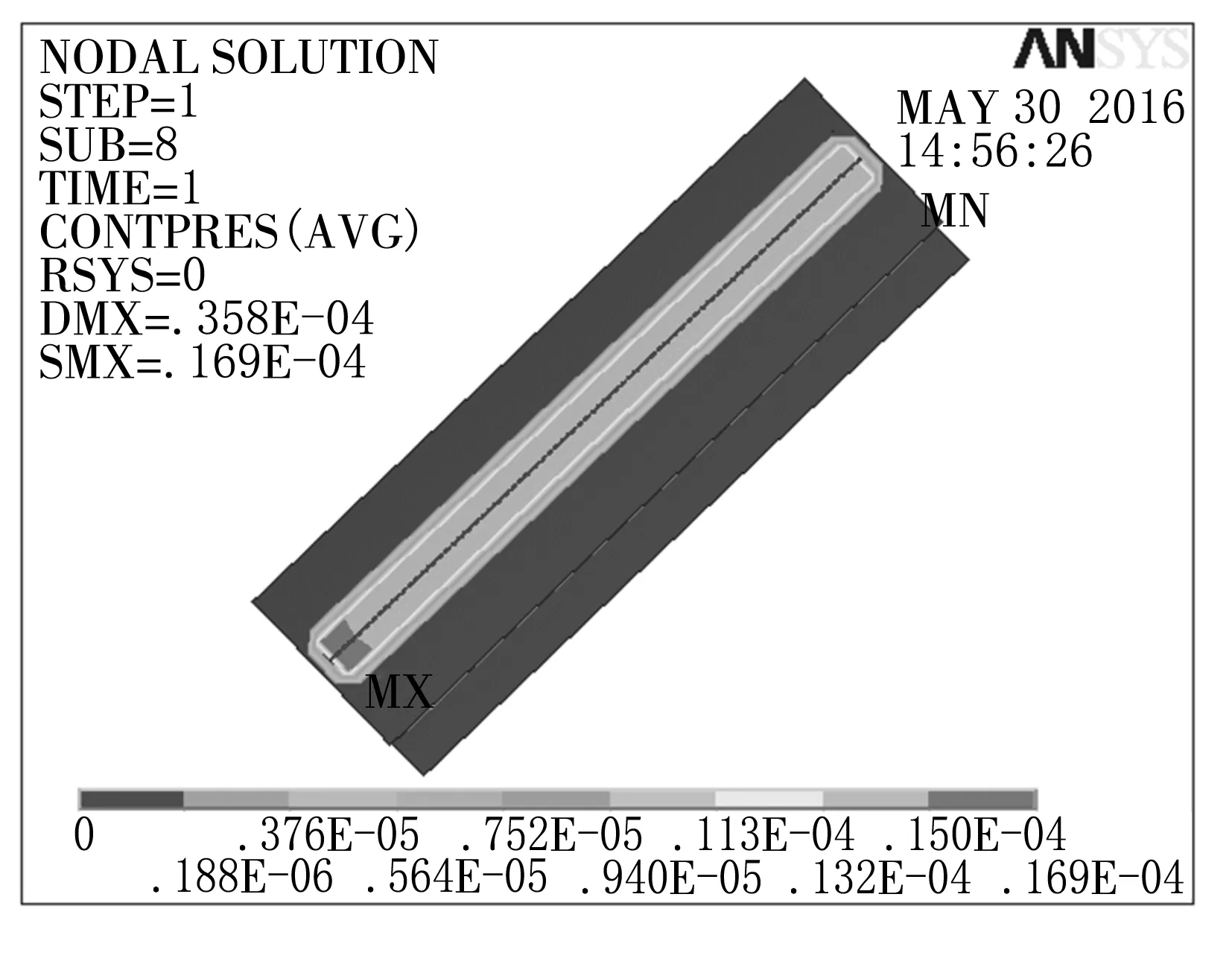
图8 外圈接触对的渗透量

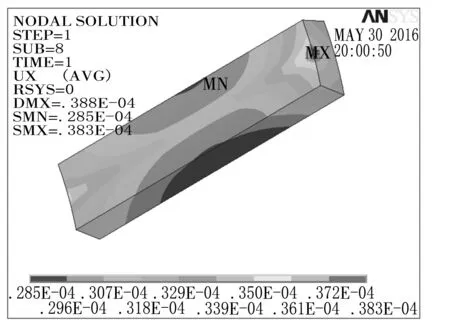
图9 内圈的变形

图10 滚柱的变形

3 滚动轴承的疲劳计算

3.1 载荷循环次数的确定

已知轴承的转速为400 r/min，假设额定寿命为可连续工作300 h，则应力幅循环次数为：

N=400×60×300=7.2×106。

(5)

3.2 滚动轴承的疲劳分析

ANSYS疲劳计算采用简化了的弹塑性假设和Miner累积疲劳求和法则。[8]在进行疲劳分析前，首先要确定此滚动轴承材料的S-N曲线，如图12所示。

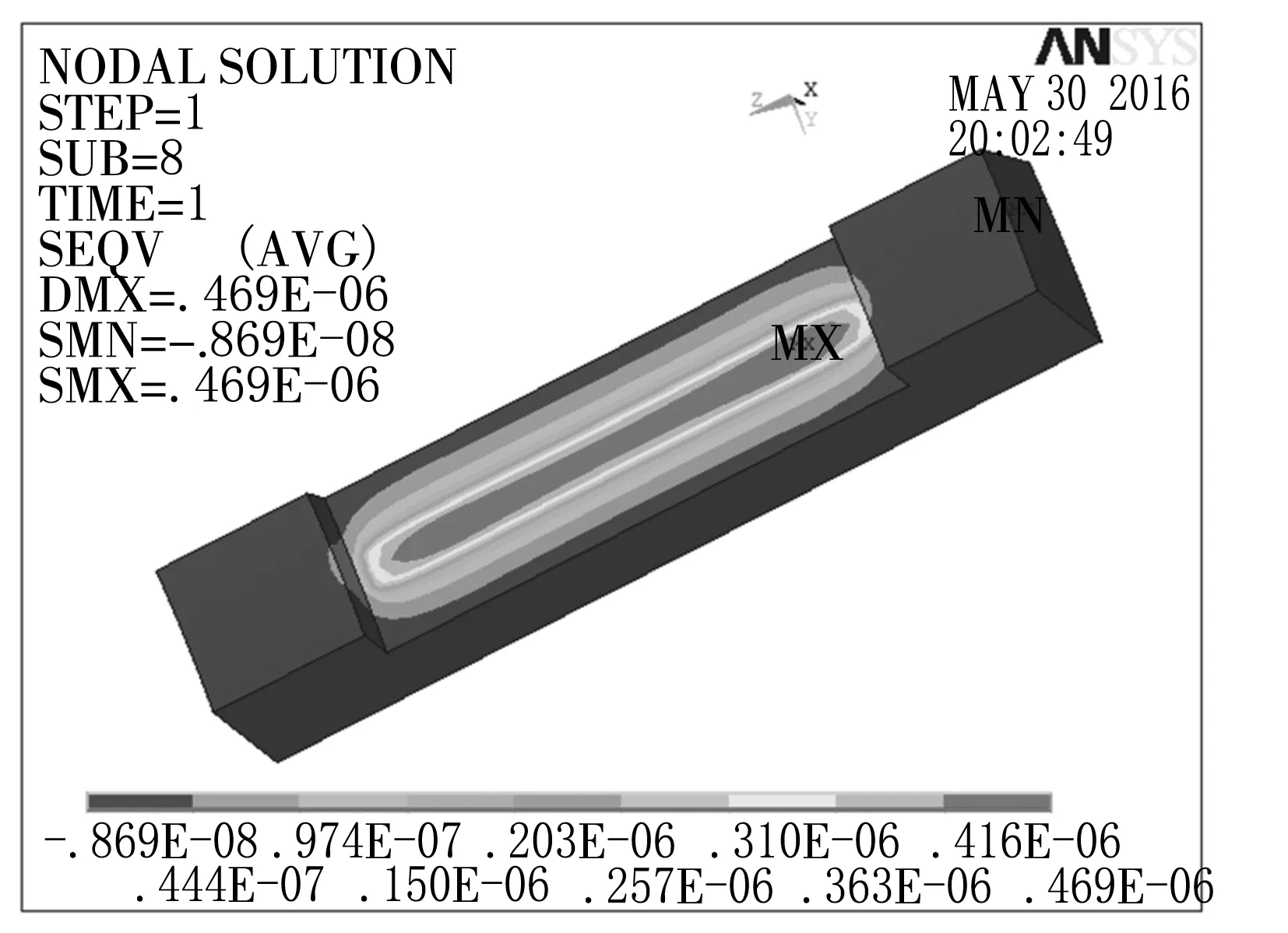
图11 外圈的变形

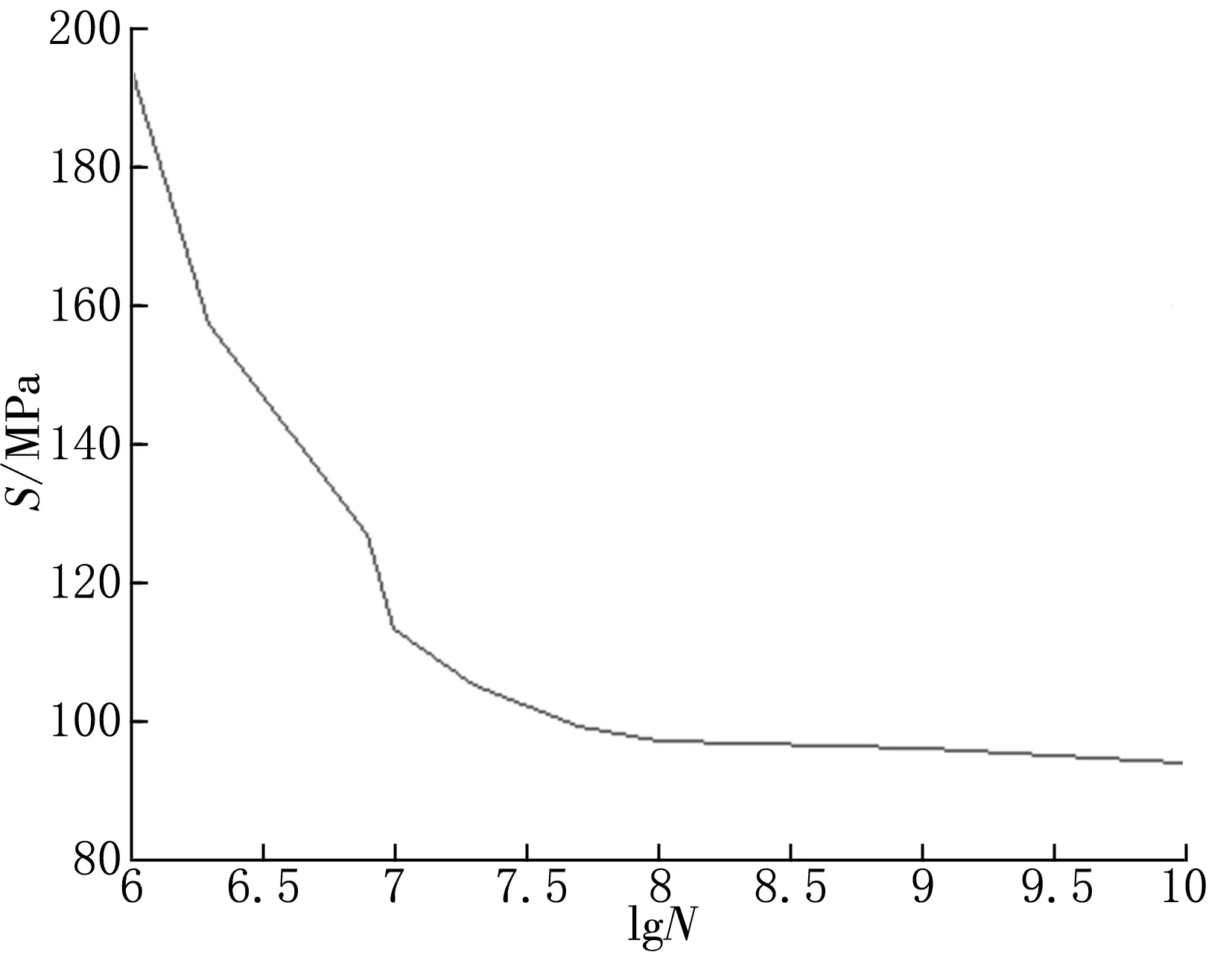
图12 轴承材料的S-N曲线

通过前面的接触强度分析，找出最大应力点后便可进行基于有限元的疲劳分析，计算结果(图13)显示该滚动轴承的疲劳系数为0.88，该值在0～1范围内，符合疲劳强度准则，表明在上述循环次数下，该轴承不会发生疲劳强度破坏。

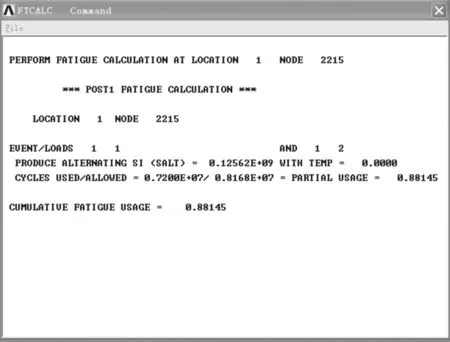
图13 ANSYS疲劳分析计算结果

4 结语

通过对滚动轴承材料显微实验以及有限元接触强度分析和疲劳计算，可得到以下结论：

1)对某滚动轴承各部件的取样进行了扫描电镜组织观察和能谱分析，得到了其具体的材料组成元素及成分近似值，并确定了材料的性能参数。

2)建立了滚动轴承的有限元接触强度分析模型，分析结果表明对于单个滚柱而言，轴承接触区域呈近似椭圆状分布，应力值由接触点向四周逐渐递减。

3)接触分析表明整个轴承的应力和变形都在允许范围内，且最大接触应力和渗透量都分布在轴承两端，滚柱最大应力发生在与内圈接触的那一侧，轴承在运行过程中最容易损坏的是内圈。

4)利用ANSYS软件对滚动轴承进行了疲劳计算，滚动轴承的疲劳系数为0.88，表明其能满足疲劳强度要求，不会发生疲劳破坏。