利用整体经验模态分解和随机森林的脑电信号分类研究

秦喜文 吕思奇 李巧玲

1(长春工业大学研究生院，长春 130012)2(长春工业大学基础科学学院，长春 130012)

引言

癫痫是一种因脑部损伤而严重影响人类健康的脑部疾病，据估计世界大约有1%的人口受到癫痫病的影响。对癫痫患者的脑电信号进行识别和分类，可以帮助医生确定癫痫发作的具体类型以便选择合理的治疗方案，帮助病人及时避开危险。因此，癫痫脑电信号识别分类的研究具有重要的理论意义和实用价值。

19世纪末期，人们开始对脑电信号(electroencephalogram，EEG)进行研究。1875年，英国的Richard Caton通过对动物进行实验记录到了它们大脑皮层的电活动[1]。1924年，Hans Berger首创了脑电图这一术语，并且首次从人类头皮上记录到脑电活动。1929年，德国耶拿大学神经科教授Berger首次发现了EEG，奠定了EEG研究的基础[2]；1934年，Berger的观察得到认同，从此人类脑电图获得科学界的认可，并被广泛应用于临床医学、心理学、药理学、脑动力学等诸多领域中[3]。

脑电信号的分析主要包括原始信号分解、特征提取、识别分类等。Johns-Gotman等提出了分解脑电信号进入半波再提取特征的方法来处理癫痫脑电信号[4]；Saab等利用小波分析来检测癫痫脑电信号的发作期[5]；Gabor等使用人工神经网络技术用来检测EEG的发作期[6]。一些学者使用时频分析相结合的人工神经网络来检测癫痫发作期，例如Ocak等采用离散小波变换分解原始信号，提取近似熵进行分类来检测癫痫发作期[7]；Oweis等提取每个固有模态函数的瞬时信息来实现模式混合分类，用来区分EEG的发作间期和发作期[8]。在基于经验模态分解的预测研究中，李淑芳等提出了一种基于经验模态分解和支持向量机分类的方法对脑电信号信号进行分类[9]；韩清鹏利用脑电信号的小波包变换与非线性分析实现精神疲劳状态的判定[10]；罗志增等使用基于双密度小波邻域相关阈值处理的脑电信号消噪方法来消除混杂在脑电信号中的噪声[11]；继Dietch使用傅立叶变换对脑电信号进行分析之后，出现了多种时域分析、频域分析的经典分析方法[12-13]。随着技术的不断发展及脑电自动分析系统的出现，利用计算机来辅助分析脑电信号逐渐受到了学者们的青睐。近年来，脑电信号分析领域相继出现了时频分析法、高阶谱分析法、非线性分析法及人工神经网络分析法等一系列现代化的分析方法[14]。

20世纪40年代脑电信号开始和临床结合，目前已在世界范围内广泛发展。脑电信号监测除了可以对癫痫，脑肿瘤，颅脑损伤，齄缺氧，缺血，脑血管疾病，中枢神经系统疾病以及新陈代谢、精神疾病和智能障碍提供诊断、预防和治疗方面的信息以外，还可以检测大脑功能、认知、思维等高级中枢活动[14-15]。但是由于EEG强烈的非平稳、非线性特性，分析起来十分困难，因此脑电信号分析方法的研究正在不断发展和日益深化。

为了提高脑电信号的识别率，本研究利用了整体经验模态分解与随机森林相结合的方法对癫痫脑电信号进行分类。

1 方法

1.1 实验统筹设计

本研究建立的EEMD-RF分类模型和EEMD-LSSVM分类模型是在Windows7系统下实现的，采用的开发平台是R*64 3.3.0和Matlab R2014a。

实验数据来自德国波恩大学癫痫数据库，该数据库包含5类脑电信号，每类脑电信号包含100个时间为23.6 s、采样频率为173.61 Hz的单通道信号，每个单通道信号包含4 096个样本点。其中，数据集A和B分别是来自5个健康志愿者的睁眼、闭眼时头皮表面脑电信号，数据集C是5个癫痫病人癫痫发作间期的海马结构脑电信号，数据集D是癫痫发作间期的致痫区脑电信号；数据集E是癫痫病人发作期的致痫区脑电信号。本研究主要分析癫痫发作间期的D数据集和癫痫发作期的E数据集。

实验首先通过Matlab实现EEMD，将癫痫脑电信号分解成多个固有模态函数。计算各阶固有模态函数与原始脑电信号的相关系数来选定有效的固有模态函数，并利用SAS计算其相关特征。最后通过R分别实现RF和LSSVM对癫痫脑电信号特征进行分类。通过对比两种方法分类结果的正确识别率，来确定哪一种分类方法对癫痫发作间期和癫痫发作期的脑电信号分类效果比较理想。

基于EEMD的癫痫脑电信号特征提取及识别分类过程如图1所示。

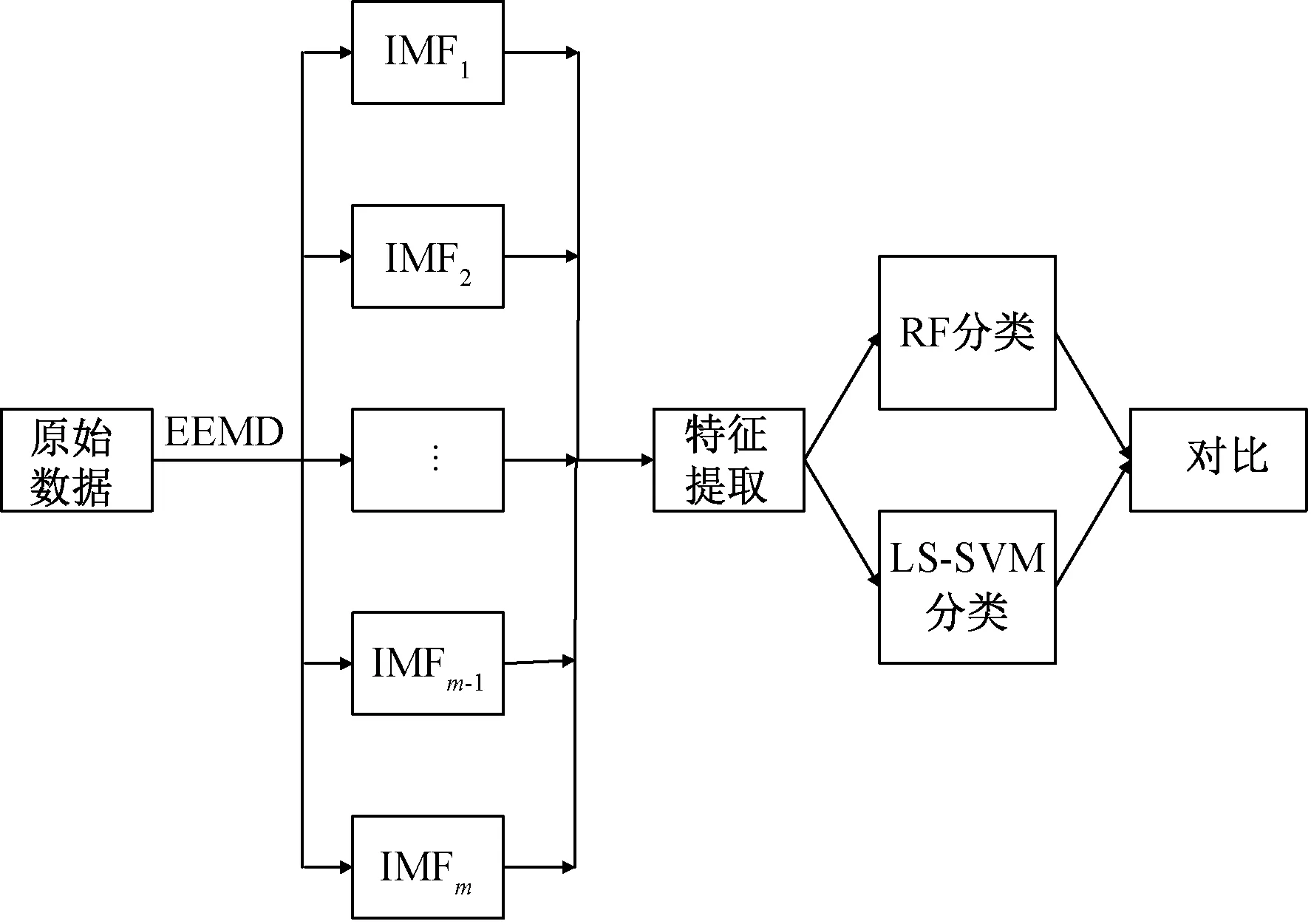
图1 发作期检测流程Fig.1 EEG ictal detection process

1.2 整体经验模态分解

整体经验模态分解(ensemble empirical mode decomposition，EEMD)方法，是在原信号中加入若干次均匀分布的高斯白噪声，用来补偿分解的固有模态函数(intrinsic mode functions，固有模态函数)丢失的尺度，再分别进行经验模态分解(empirical mode decomposition，EMD)处理，最后求平均的一种全局化方法[16]。该方法令加入的白噪声互相抵消，不仅保留了原序列的信号信息，很大程度上克服了模态混叠问题，使分解在物理上唯一。EEMD算法流程如图2所示。

图2 EEMD算法流程Fig.2 EEMD algorithm flow chart

EEMD具体步骤[17]如下：

1)通过给待分析信号x(t)中加一组白噪声w(t)，构成信噪混合体，即

X(t)=x(t)+w(t)

(1)

2)对信噪混合体X(t)进行EMD分解，将其分解成各个IMF分量的组合，即

(2)

3)给待分析信号加入不同的白噪声w(t)，重复以上两步，有

Xi(t)=x(t)+wi(t)

(3)

分解后得到各自的IMF分量组合，即

(4)

4)对所有IMF组合相对应的IMF求平均，即

(5)

式中，N表示整体的个数，即得到最后分解结果，有

(6)

因白噪声的零均值特性，加入噪声的次数足够多，将这些多次分解的结果取“平均”后，噪声最终将被互相抵消从而达到消除的效果，整体平均的结果就可以被当作真实信号。

选取波恩数据集中癫痫发作间期与发作期的各100个单通道信号，分别进行整体经验模态分解。计算各阶固有模态函数与原始脑电信号的相关系数，并选取合适的IMF进行以下分析。

1.3 特征提取

对整体经验模态分解后得到的各阶固有模态函数提取重要特征，包括均值、方差、标准差、极差、变异系数、波动指数、能量熵和信息熵等。

1.3.1变异系数

对脑电信号幅度进行分析时，经常选择使用的特征有平均值、方差、标准差、变异系数等简单统计量，其中变异系数能够衡量脑电信号的幅度变化。对于癫痫发作间期的脑电信号等幅度变化规则的信号，变异系数的值比较小，其定义为

CV=σ2/μ2

(7)

其中

式中，l为固有模态函数的长度。

1.3.2波动指数

波动指数可以衡量信号变化的强度。癫痫发作期信号的波动通常会比发作间歇期的波动剧烈。其定义为

(8)

式中，l为固有模态函数的长度。

1.3.3能量熵

为了便于特征提取，选择能量熵来表征不同固有模态函数特征的差别。根据信息论中能量熵的定义，固有模态函数ci(t)的能量的计算公式见后，t1和t2分别为信号起始时间和结束时间[16]，有

(9)

其定义为

(10)

式中，Pi=Ei/E为第j个固有模态函数的能量占整个信号能量的比例，E为整个信号的能量。

1.3.4信息熵

信息中排除了冗余后的平均信息量称为“信息熵”，癫痫发作期信号的信息熵通常会比发作间期的信息熵低，其定义为

(11)

式中，x表示随机变量，与之相对应的是所有可能输出的集合，定义为符号集。

选取波恩数据集中发作间期与发作期IMF1～IMF5来计算相关特征，分别为均值、方差、标准差、极差、变异系数、波动指数、能量熵、信息熵等。

1.4 随机森林

随机森林(random forest，RF)最早是由Breiman[18]于2001年提出来的， 是一种非参数统计方法，它的基本思想是用bootstrap方法从原始样本中抽取多个子样本，对每个bootstrap子样本进行决策树建模， 再利用投票法或者平均法组合多棵决策树的预测结果来决定最终预测结果。

随机森林相对于神经网络、支持向量机、决策树等方法具有更好的噪声容忍度以及更高的预测准确率，且不容易出现过拟合问题。随机森林是由若干树形分类器{h(x,θk),k=1,…}组成的集成分类器，其中x是输入向量，{θk}是独立同分布的随机向量，预测时通过简单的多数投票法、或单棵树输出结果的简单平均得到随机森林的最终输出。具体步骤[19]如下：

步骤1：用Bagging方法形成个别训练集，即每个个别训练集都是从原始训练集的n个样品中有放回地抽取n个样品。

步骤2：对于每个个别训练集，用如下过程生成一棵不剪枝的分类回归树。

1)设共有M个原始属性，给定一个正整数mtry，满足mtry≤M。在每个内部节点，从M个原始属性中随机抽出mtry个属性作为该分裂节点的候选属性。在生成整个森林的过程中，mtry不变。

2)从mtry个候选属性中选出最好的分裂方式对该节点进行分裂。

3)每棵树令其充分成长，不进行剪枝。

3)重复1)和2)，直到生成ntree棵分类回归树(ntree足够大)。

4)对未知类别的样本进行分类时，输出的类别标签由森林中树的多数投票决定，即

(12)

随机森林在Bagging的基础上引入随机选择属性，更大程度上降低了树之间的相关性，同时建立的单棵不剪枝的分类回归树能够得到较低的偏差，从而保证了随机森林的分类性能。

在K折交叉验证中，原始样本组随机划分成K个样本的平均子集。在K个子集中，单个子集用于测试模型的测试数据，剩余的K-1的子集被用作训练数据，将交叉验证过程重复K次，每个恰好一次作为验证数据，在K个结果后可以进行平均或以其他方式组合来产生一个单一的估计。本研究选择使用四折交叉验证。

在RF分类过程中，提取IMF1-IMF5的均值、方差、标准差、极差、变异系数、波动指数、能量熵和信息熵之后组合形成特征矢量，训练数据的特征矢量被送入一个RF分类以获得最佳的RF参数。最后，经训练的RF分类器用于区分测试集中的脑电信号类别。

1.5 最小二乘支持向量机

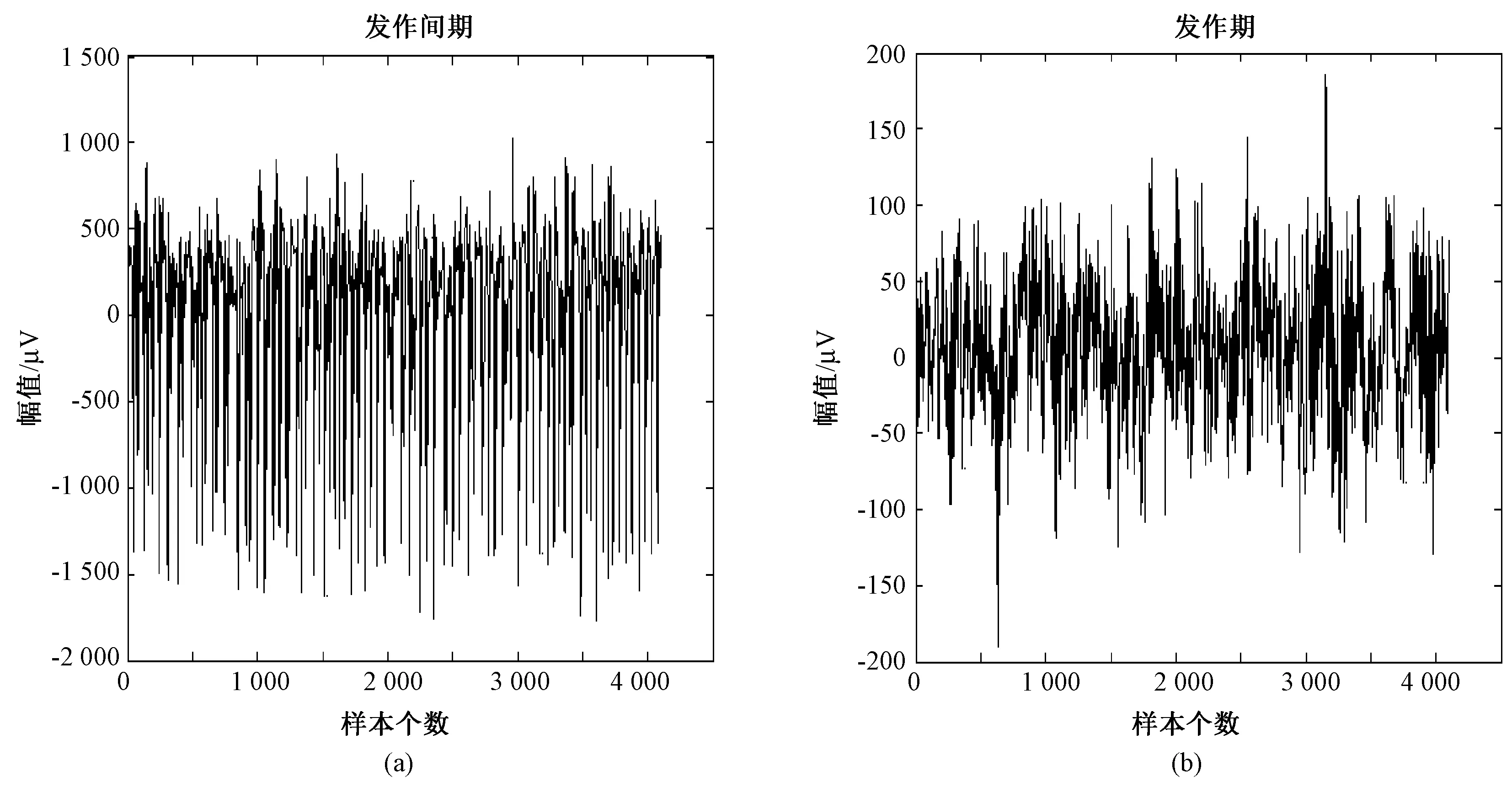
图3 癫痫发作间期和癫痫发作期的样本。(a)癫痫发作间期样本；(b)癫痫发作期样本Fig.3 The sample of of ictal and interictal EEG. (a) The sample of of interictal EEG;(b) The sample of of ictal EEG

最小二乘支持向量机(least squares support vector machine，LSSVM)是传统支持向量机(support vector machine，SVM)的一种改进方法，其基本思想是基于Mercer核展开定理[20]将传统支持向量机中的选取误差ei和不等式约束改为选取误差的二范式和等式约束[21]。与SVM算法相比，LSSVM算法简化了计算的复杂度，降低了预测误差，保证了计算结果的准确性。

假设训练样本集(xi,yi)(i=1,2,…,N)，其中xi∈Rm为训练样本输入，yi∈R为训练样本输出。通过径向基核函数φr(*)将低维空间Rm向高维特征空间映射，在高维空间中构建最优决策函数，根据结构风险最小化原则构建优化模型，即

(13)

约束条件为

yi=WTg(xi)+b+ξi(i=1,2,…,M)

(14)

由于W一般情况为无限维的，很难直接计算优化模型，通常将这一规划问题转化到其对偶空间中。根据Hilbert-Schmidt原理，通过引入满足Mercer条件的核函数K(xi,xj)=φ(xi)Tφ(xj)，将变换空间中内积计算问题转化为原空间中某个函数的计算问题，间接求解输入空间向高维特征空间的映射。最终得到LSSVM回归函数为

(15)

在LSSVM分类过程中，选取发作间期和发作期数据集的前75%特征矢量作为训练样本，后25%特征矢量作为测试样本，采用交叉验证的方法求出最佳参数来得到训练好的LSSVM分类器。将测试样本送入该分类器，进行多次试验得到平均分类结果。

2 结果

2.1 癫痫脑电信号分解

选取癫痫发作间期的D数据集和癫痫发作期的E数据集进行分析。原始癫痫脑电信号发作间期和发作期的样本如图3所示。

图3(a)为癫痫发作间期脑电信号样本。选取波恩数据集D的200个单通道信号中的1个单通道信号，包含4 097个样本点。可以看出该信号波幅较大，具有规律性。图3(b)为癫痫发作期脑电信号样本。选取波恩数据集E的200个单通道信号中的1个单通道信号，包含4 097个样本点。可以看出该信号波幅较小，且不稳定。

由图3(a)、(b)可以看出，癫痫发作间期脑电信号与癫痫发作期脑电信号波动差距明显。

对癫痫脑电信号进行整体经验模态分解得到各阶固有模态函数，通过计算各阶固有模态函数的相关系数，选定了IMF1～IMF5来提取特征并计算。癫痫发作间期和癫痫发作期EEG某一个时间段的前5个固有模态函数在图4给出。图4(a)为癫痫发作间期脑电信号经整体经验模态分解后的固有模态函数，选择波恩数据集D中的100个单通道信号中的1个单通道信号作为样本。整体经验模态分解后的癫痫发作间期脑电信号得到了8个固有模态函数和1个趋势项。图4(b)为癫痫发作期脑电信号经整体经验模态分解后的固有模态函数，选择波恩数据集E中的100个单通道信号中的1个单通道信号作为样本。整体经验模态分解后的癫痫发作间期脑电信号得到了8个固有模态函数和1个趋势项。

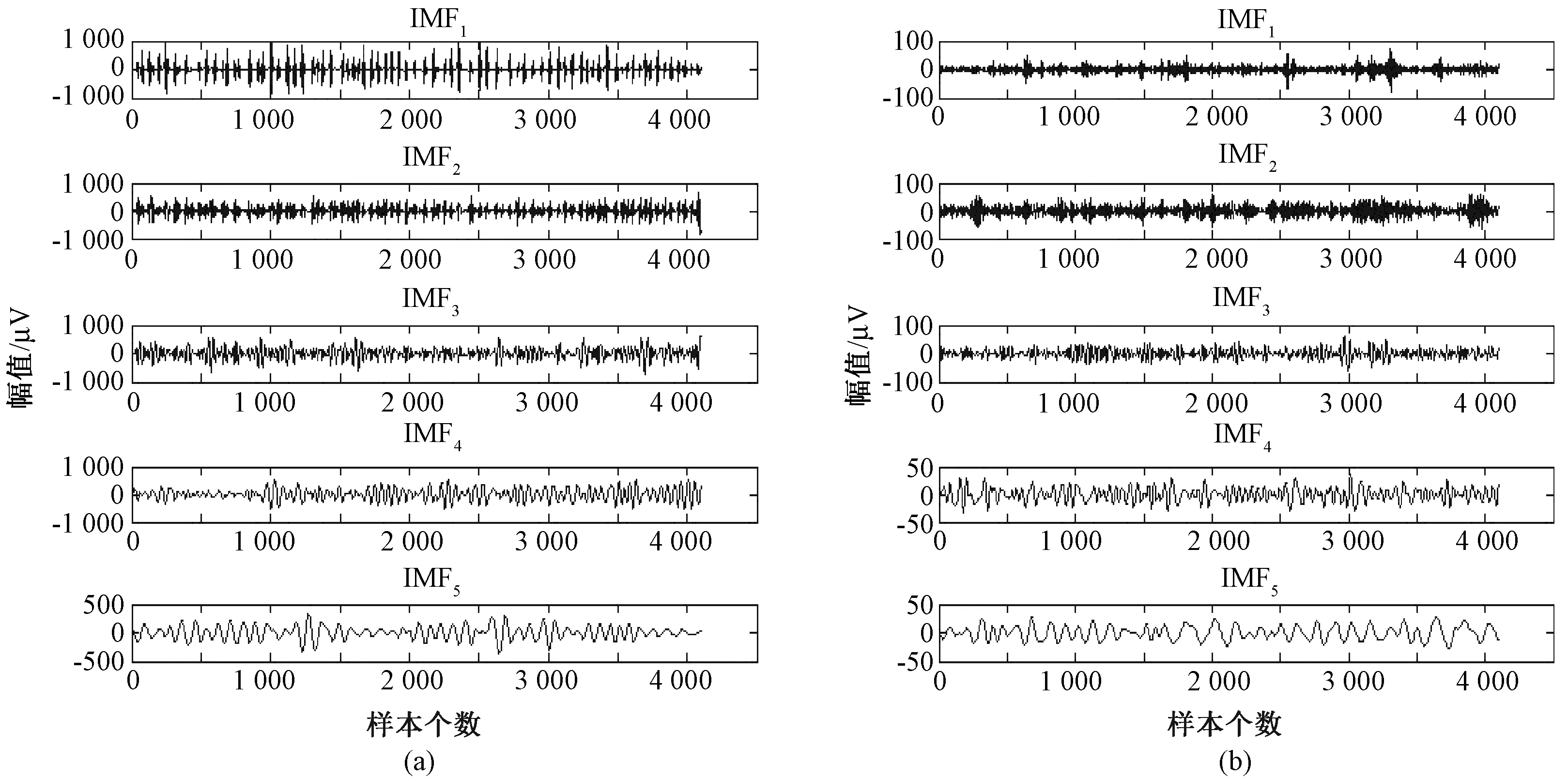
图4 发作间期和发作期EEG一个时期的前5个固有模态函数。(a)发作间期；(b)发作期Fig.4 The top five IMFs of ictal and interictal EEGs on Bonn data sets.(a) The interictal EEG; (b) The ictal EEG

表1 癫痫脑电信号发作间期特征样本Tab.1 The sample of interictal EEG features

表2 癫痫脑电信号发作期特征样本Tab.2 The sample of ictal EEG features

由图4(a)、(b)可以看出，癫痫发作间期脑电信号和发作期脑电信号波幅和频率都存在很大差别。接下来对整体经验模态分解后得到的各阶固有模态函数计算相关系数。

2.2 癫痫脑电信号特征提取

对癫痫脑电信号发作间期与发作期的200个单通道信号，经过整体经验模态分解后计算相关系数选取的前5个固有模态函数进行特征提取，主要选取均值、方差、标准差、极差等简单统计量及变异系数、波动指数、能量熵、信息熵作为特征，用于接下来的分类。

表1、2分别为波恩数据集癫痫脑电信号发作间期与发作期的特征结果样本，以1个单通道信号为例，经过整体经验模态分解后计算各阶固有模态函数与原始脑电信号的相关系数，选取了IMF1～IMF5来计算相关特征，分别为均值、方差、标准差、极差、变异系数、波动指数、能量熵、信息熵。

2.3 癫痫脑电信号识别分类

本研究分别选取RF和LSSVM两种方法对固有模态函数进行分类，并对结果进行比较。将固有模态函数所有特征和其组合进行分类的结果汇总(见表3)，表明利用RF对IMF1～IMF5组合特征进行分类效果最佳，最高的正确识别率为99.60%。

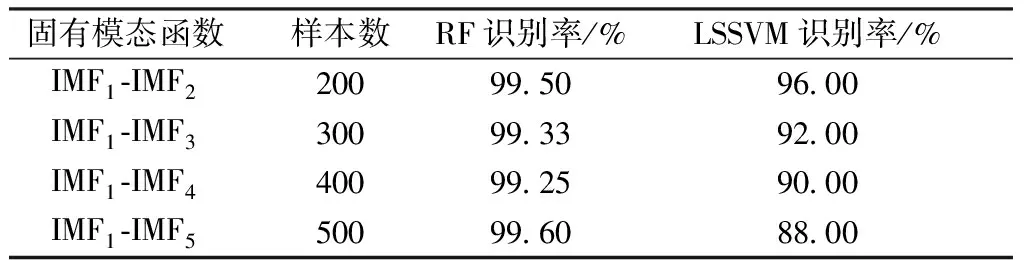
表3 癫痫脑电信号分类结果比较Tab.3 The compare of EEG classification result

通过实验结果可以发现，EEMD～RF方法选择IMF1-IMF5的特征对发作间期和发作期EEG分类效果最佳，表现为99.60%的正确识别率，EEMD-LSSVM方法选择IMF1～IMF2的特征对发作间期和发作期EEG分类效果最佳，表现为96.00%的正确识别率。经对比发现，EEMD-RF方法对EEG的分类准确性优于EEMD-LSSVM方法。

3 讨论

一种有效的癫痫脑电信号分类方法在临床诊断与治疗中是至关重要的。李淑芳等提出了一种基于EMD和SVM结合的脑电信号分类方法[9]，李营等在关于癫痫脑电信号的研究中提出了基于此方法的改进方法[16]，即EEMD与LSSVM结合的癫痫脑电信号分类方法得到了较好的分类效果，这证实了基于EMD 的信号分解方法与基于机器学习的分类方法相结合对于脑电信号分类的效果是显著的。李营等[16]在研究癫痫脑电信号问题时选取了整体经验模态分解与最小二乘支持向量机结合的分类方法对脑电信号进行分解与分类，证明了整体经验模态分解方法在癫痫脑电信号分类研究中能够有效分解癫痫脑电信号并保留有意义的信息。

EEMD在时频分析领域具有很大的优势，尤其是处理非线性和非平稳信号，可以保持EMD的优势并解决EMD中的端点效应及模态混叠问题。除了脑电信号分解，还可以广泛应用于其他领域，比如故障诊断、气象预报等。相较于目前的其他分类算法，RF能很好地抗噪声和抗干扰能力，作为有监督的学习方法不容易出现过拟合现象，对于不平衡的分类资料来说可以平衡误差。RF自算法提出以来已经成为一种非常重要的分析方法，并可以广泛应用于其他领域，包括基因数据、核磁共振光谱、土地分类等。在此基础上，本研究提出了一种基于EEMD和RF的新的癫痫脑电信号分类方法。

张学清等在混沌时间序列分析中用近似熵作为特征进行预测[20]，张超等在齿轮故障诊断识别应用中使用能量熵作为特征进行有效的分类[21]，表明在不同的数据中可以得到最优分类的特征并不固定，本研究中选取多种特征进行组合及分类，选取最优的分类结果。

通过对德国波恩大学癫痫脑电数据进行实证分析，结合EEMD的自适应分解特性与RF的抗干扰和避免过拟合优点，将EEMD-RF算法分类结果的正确识别率与EEMD-LSSVM算法分类结果的正确识别率进行对比，结果表明，EEMD-RF方法对癫痫发作间期和癫痫发作期脑电信号分类效果明显优于EEMD-LSSVM方法。该方法不仅可以应用在生物医学信号分析处理方面，还可以应用于金融数据、机械故障诊断、环境预警等其他众多领域，为在不同领域研究分类识别与预警预报等问题提供了可行的思路和模式。

4 结论

脑电信号中存在着大量生理与病理信息，脑电信号的识别与分类在癫痫疾病的检测与辅助治疗中发挥着极其重要的作用。本研究对癫痫脑电信号的分析显示：与EEMD-LSSVM方法分类结果相比，对癫痫脑电信号进行EEMD分解，选取IMF1-IMF5的能量熵和信息熵等属性作为特征，通过实现RF分类对癫痫发作间期和癫痫发作期脑电信号进行特征识别和分类的结果精确度更高，表现为99.60%的正确识别率，即EEMD-RF方法对癫痫发作间期和发作期脑电信号分类效果更佳。本研究提出的方法对癫痫的自动监测具有重要的理论意义与实用价值，可以为病人及时提示和预警，为医护人员提供科学的决策支持。

(致谢：感谢德国波恩大学癫痫研究中心提供数据支持！)