混凝土拱坝位移确定性监控模型研究

李明军，王均星

(武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072)

大坝安全监测监控模型主要应用的有3种：统计模型、确定性模型、混合模型。确定性模型相对于其他两种模型有更明确的物理概念，可以更好的联系大坝和坝基的结构性态，具有更好的预测效果[1]。温度位移分量的确定一直是建立位移确定性监控模型的难点。混凝土拱坝的整体性较好，大坝承载能力较强但坝体结构对温度变化十分敏感，温度边界条件复杂且温度位移分量在总位移中占有比重较大，在建立混凝土拱坝的位移确定性监控模型时一般要求有能全面反映坝体温度变化的温度实测资料。而目前很多大坝在温度监测方面只有环境温度资料，尤其是对于长期运行以后(一般50年及以上)的大坝，由于建设时坝体内温度计埋设不合理，或是运行后温度计失效，无法获得完整的坝体温度实测资料，限制了确定性模型的应用。

目前，国内外对大坝位移确定性模型的研究主要适用于在坝体内部温度场确定的情况，当缺乏坝体温度实测资料时，利用边界温度推求温度位移分量值是建立大坝位移确定性模型的唯一方法，非此就不能建立确定性模型[2,10]。但是由于拱坝温度初始条件和边界条件复杂，其温度荷载很难准确模拟，为确定温度位移分量带来了极大的困难。李步娟[3]提出用“单位边界温度模型”计算测点的位移温度分量，但由于测点位移变化滞后于边界温度变化，需要深入分析不同测点的滞后规律，其应用具有明显局限性。李端有[4]采用朱伯芳法以气温估算库水温度，再通过气温和水温确定拱坝边界条件，以单个的坝体测点实测温度值检验大坝计算温度场，在此基础上使用有限元数值分析法建立拱坝位移确定性模型，然而此种方法要求在坝体内布置有效温度计以获取坝体实测温度资料，在坝体内未埋设温度计或者有效温度计数量极少且测点分布不均匀的情况下并不适用。

对于运行多年的混凝土拱坝，其运行期任意时刻位移温度分量由坝体内部温度场决定。坝体内部温度场受坝体外部温度影响且滞后于坝体外部温度。坝体外部的环境温度是由气温、大坝上游水库水温所组成的[5][12]。当利用边界温度推求温度分量值时，不可避免的提出一些假定，这些假定的提出让温度场计算变得简单，却使得由边界温度推求的拱坝温度场与实际温度场存在一定的差异，当缺乏实际坝温监测资料来对拱坝计算温度场进行修正时，如何校验拱坝温度场，提高确定性模型的精度成为一个有待解决的问题。而对运行多年的混凝土拱坝实测位移分析表明，拱坝位移的变化(尤其是径向位移)受环境温度变化的影响非常明显，位移随温度做一定的周期性变化。在正常情况下，对于长期运行的混凝土拱坝而言，坝体自重保持不变，位移的改变主要是由于水位、温度以及时效变形引起的，而运行期时效变形趋于稳定。通常情况下，在一年中，时效位移小于1%的总位移(例如，一个130 m的高度拱坝，热位移振幅约为20 mm，而其不可逆的趋势是每年约0.1 mm)[6]。因此可以认为在任意时段Δt内，当Δt比较小时(Δτ<1 a)运行期混凝土拱坝位移的改变主要是由于水位和温度变化引起的，即在 时段内，由温度和水位变化所引起的位移变化值与该时间段内实测位移变化值应该保持一致，而水位变化所引起的位移改变是确定的。以此对拱坝实际温度场进行检验。

针对运行期拱坝这一变形特点，提出以环境温度(主要是气温与水温)建立大坝温度边界条件，采用有限元法分析大坝实时温度场，选取短时间实测位移序列校验大坝温度场，建立运行期拱坝位移确定性模型。这为我国大部分缺乏坝体温度监测资料的运行期混凝土拱坝的安全监控提供了一个新思路。

1 混凝土拱坝温度场的确定

1.1 有限元热力学计算原理

在区域Ω内，准稳定温度场T(x,y,z,τ)应满足热传导方程：

(1)

初始条件：

T(x,y,z,τ0)=T(x,y,z)

(2)

设区域Ω的边界为Γ，则拱坝温度场的边界条件[7]：

(1)第一类边界条件：

(3)

(2)第三类边界条件：

T(x,y,z,τ)|(x,y,z),Γ1=g(x,y,z,τ)

(4)

式中：α为导温系数，m2/h；T0(x,y,z)为初始温度，℃；g(x,y,z,τ)为边界温度，℃。

根据变分原理，任意时刻τ温度场为：

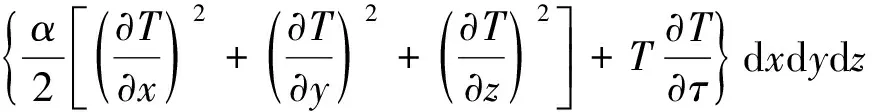
(5)

当温度T在τ=τ0时，T=T0，边界Γ1上的边界温度为g(x,y,z,τ)。当式(5)所示泛函I(T)取极小值，温度场T在区域Ω内满足热传导方程(1)，且在边界Γ2上满足公式(3)，准稳定温度场T则确定了。

将区域Ω用有限元离散，则泛函I(T)变成在各单位内的积分，即：

I=∑Ie

(6)

其中，Ie为单元e内的积分，即：

(6)

式中：ΔΩ为单元e所包含的子域。

对式(7)在积分号内求导，则有：

(8)

泛函取极值，有：

(9)

设单元e的结点温度为：

{T(τ)}e=[Ti(τ),Tj(τ),Tm(τ),LL]T

(10)

则单元内任一点的温度：

T(x,y,z,τ)=[Ni(x,y,z),Nj(x,y,z),

Nm(xy,z),LL]{T(τ)}e=[N]{T(τ)}e

(11)

将公式式(11)代入公式(8)，通过式(9)可得到方程组：

[K]{T}+[C]{T}=0

(12)

式中：[K]为热传导矩阵；[C]为热传导矩阵；[T]为结点温度向量；{T}为结点温度向量随时间的变化率。

求解方程组(12)，就可以得到所有结点的温度值。

1.2 混凝土拱坝温度边界条件的拟定

当缺乏详细的温度资料来描述大坝实时温度场时，一般采用气温来估算坝前水温、拟定坝体温度场的边界条件，再通过有限元法得到大坝实时温度场，进而建立大坝位移确定性模型。

采用气温估算坝前水温的常用方法有华东勘院法、朱伯芳法、数学模型法等。目前混凝土拱坝主要采用朱伯芳法，其计算公式简单，通过月平均温度和坝前水深，综合水库地理位置，估算坝前垂直方向的水温分布，具有良好的工程应用效果[7,11,14]。具体计算方法如下：

坝前任意水深处y处的水温变化为

T(y,τ)=Tm(y)+A(y)cosω(τ-τ0-ε)

(13)

式中：Tm(y)为y处的年平均温度，Tm(y)=c+(b-c)e-ay；A(y)为y处的温度年变幅，A(y)=A0e-βy；ω=2τ/p,p为温度变化周期，这里p=12月；τ0=6.5月(因τ=τ0时气温最高)；ε为水温与气温的变化相位差，ε=e-fe-γ；α、β、γ、d、f等都为相关的参数。

朱伯芳法假设坝前水位是正常蓄水位，其计算公式对水库坝前水深小于100 m的工程应用效果较好。当水位变幅较大且坝前水深超过100 m时，采用朱伯芳法计算会产生较大误差。当运行水位高于或等于正常蓄水位时，朱伯芳法的估算精度能满足工程需求，否则需要对朱伯芳库水温度估算公式进行改进[7]。

由于库水温度与水深 有关，当坝前水位为实际运行水位时的水温用 表示，相应的气温用 表示， 为运行水位，当坝前正常水深H>100 m时， 用分段函数表示：

(14)

改进的朱伯芳法估算的库水温度能更好地符合实际温度边界条件，使有限元计算温度场能更好地符合拱坝实际温度场，为提高位移确定性模型精度提供更好的基础。

按照前文所述方法所拟定的混凝土拱坝温度边界条件与实际情况并不相同，由此所得到的混凝土拱坝温度场不可避免与实际温度场存在一定的差异。不同混凝土拱坝对于这种差异的响应并不相同，主要表现为位移监控模型中的精度。

1.3 混凝土拱坝温度边界条件的检验

按照前文所述方法所拟定的混凝土拱坝温度边界条件与实际情况并不相同，由此所得到的混凝土拱坝温度场不可避免与实际温度场存在一定的差异。不同混凝土拱坝对于这种差异的响应并不相同，主要表现为位移监控模型中的精度差异[8,9]。为了验证混凝土拱坝温度边界条件的合理性，本文针对缺乏坝体温度实测资料的运行期(一般运行10年及以上)混凝土拱坝的变形特点，提出一种校验混凝土拱坝拟定的温度边界条件合理性的新方法。

在正常运行条件下，对于长期运行的混凝土拱坝而言，坝体自重保持不变，位移的改变主要是由于水位、温度以及时效变形引起的，而运行期时效变形趋于稳定。本文采用有限元法计算任意时间段Δt(Δt≤1 a)内拱坝的变化温度场，由热-结构的耦合得到在 时段内温度变化所引起的位移变化值，由于水位变化引起的位移是确定的，其与该时段内水位变化所引起的位移变化值叠加与同时段内实测位移变化值应该保持一致，即：

(15)

若能满足此条件，则证明温度边界条件拟定的合理，若不能满足此条件则根据实际资料对混凝土拱坝温度边界条件进行修正。

2 位移监控模型的建立方法

大坝位移确定性模型通过物理理论计算成果来构造环境自变量与大坝变形联系的确定性关系式，其建立的基本思路为假设坝体和地基材料的力学参数与时效的数学模型，采用有限元法计算大坝观测控制点在荷载作用下的坝体和坝基的位移场，通过此计算值与实测值进行最小二乘法拟合，求得大坝变形影响因子的调整参数以及时效位移分量参数，从而建立大坝位移确定性模型[13,16]。影响混凝土拱坝变形主要有三个因素：水位，温度以及时效，其相关表达式为：

(16)

(17)

δθ=C1θ+C2lnθ

(18)

δ=XδH+YδT+δθ

(19)

式中：δ为测点总位移；δH、δT及δθ分别为水压、温度及时效位移分量；H为坝前水深；T为一定时间段内的气温平均值；θ为时间；C1、C2为待定系数；X、Y为调整系数，其中系数在总位移模型时根据实测资料利用回归方程求出。

位移确定性监控模型的难点是有效的确定温度边界条件，得到与实际情况符合的拱坝实时温度场，从而提高确定性模型的精度。在利用1中所论述的方法，拟定拱坝的温度边界条件，计算拱坝初始温度场，选取时间段Δt(Δt<1 a)，计算此时间段内的温度位移变化值，将其与 时段内实测位移变化值和水位变化引起的位移变化值之差进行比较，当误差值小于10%，则认为此次温度场边界条件拟定合理，否则根据实测资料对温度边界条件进行修正，重新计算直到满足条件。

3 工程实例

东江大坝为混凝土双曲拱坝，其左右岸基本对称，坝顶高程294.0 m，坝底高程137.0 m，坝高157.0 m，设计正常蓄水位285 m。东江拱坝于1986年开始蓄水，已安全运行二十余年，荷载基本于左右对称，其中11#，为中间坝段。由于拱冠15号坝段所在测点监测资料部分丢失，因此本文拟将靠近拱冠梁位置的11#坝段的前方交会的8号测点作为研究对象，认为此位置测点在外部荷载作用下能反映整个拱坝的工作性态。

依据东江大坝的坝型及基础地质资料，选择坝体和一定范围内的坝基为研究对象，确定坝体和坝基的弹性模量、线膨胀系数、热传导系数等物理力学参数，将测点作为单元节点来划分计算单元网格，从而建立拱坝和坝基的三维有限元分析整体模型。模型的计算范围为：坝轴线上、下游分别取350、250 m；坝底向基岩延伸150 m；左、右岸各取250 m。其中左岸方向为x轴正方向，下游方向为y轴正方向，z轴向上为正。整个模型可以分成两个部分：坝体部分以及拱坝基础部分。其中坝体部分除坝身外主要包括的细部结构有：左右岸溢洪道，坝间分缝，闸墩，坝后背管以及横向廊道。拱坝基础部分则包含重力墩以及岩体。由于本文主要研究重点为坝体，故而将左右溢洪道只模拟其与坝体相关联部分，忽略廊道作用，而拱坝的分缝则使用薄层来模拟。由东江拱坝多年运行经验可知东江拱坝基础中存在的岩层软弱带与岩层破碎带范围小，对大坝运行影响可以忽略不计，因此，基础除重力墩以外部分视作整体，不考虑岩层破碎带的影响。东江拱坝三维有限元数值模型如图1，上、下游方向取y向法向约束，左右岸方向取x向法向约束，底面取z向法向约束。其单元数71 061个，节点数96 471个，其中坝体单元43 318个，坝基单元27 743个。

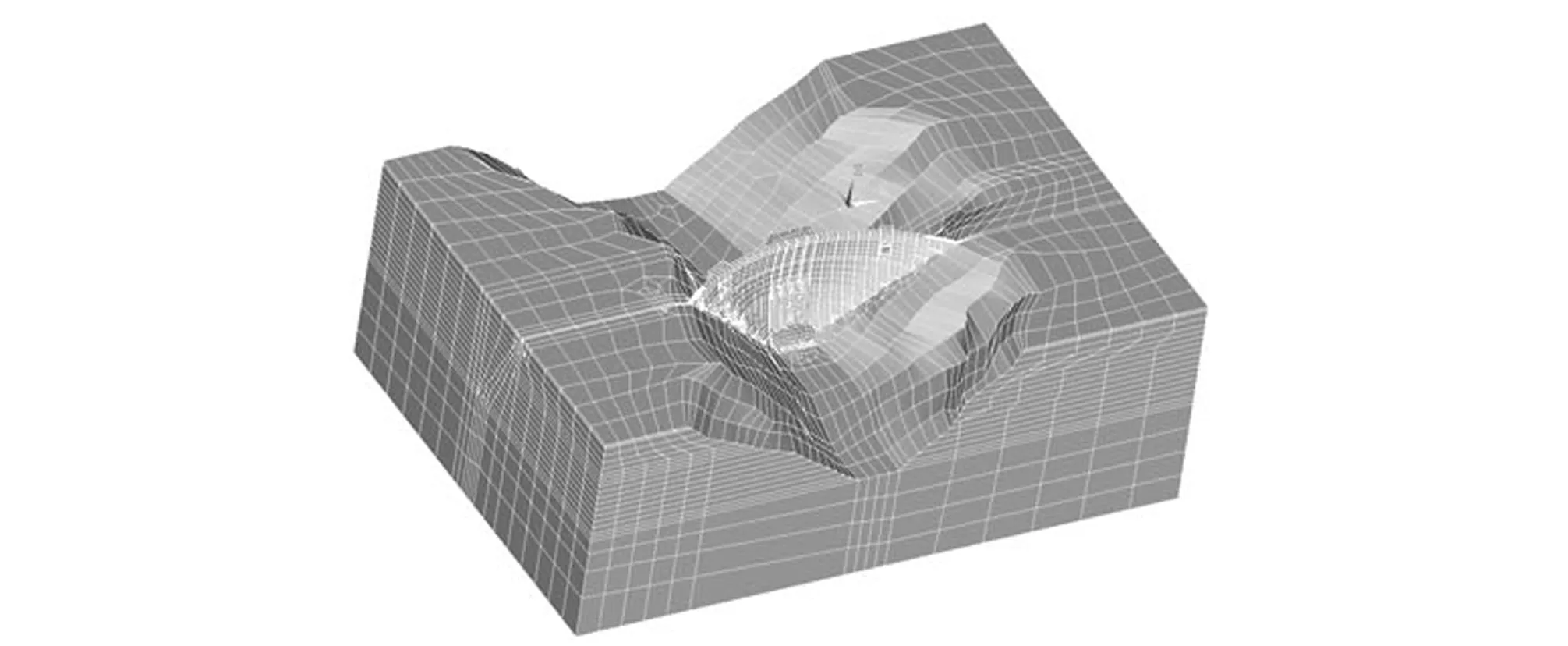
图1 东江拱坝有限元计算模型Fig.1 The finite element calculation model of Dongjiang arch dam

3.1 温度场的计算

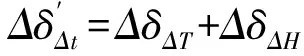
表1 292 m高程处8号测点计算温度与实测温度对比Tab.1 Comparison of the calculated temperature and measured temperature at 8 points of 292 m height

表2 292 m高程处8号测点计算位移与实测位移对比 mTab.2 Comparison of the calculated displacement and measured displacement at 8 points of 292 m height

由表1与表2中的温度变化所引起位移变化的分析表明，采用有限元法分析计算拱坝坝体变化温度场是可行的。当计算变化温度场与实测温度场较符合时，且 较小时，由此计算的由水位变化和温度变化引起的位移变化值与实测位移变化值相差很小。当 增大的时候，误差绝对值增大，但是其数值依然小于2 mm，这是由于运行期混凝土拱坝的时效变形比较稳定的缘故。因此，在坝体没有埋设温度计，或者温度监测资料不完整的条件下，可以通过有限元法计算坝体温度场，再采用本文所述方法，即公式(3)检验假定坝体温度边界条件，从而提高位移确定性模型精度。

3.2 温度位移分量计算结果

通过有限元数值分析方法计算东江拱坝温度场，由热-结构耦合分析求得温度荷载作用条件下的坝体位移。11号坝段前方交会8号测点在2003年2月-2012年12月时段内的温度位移分量变化过程线如图2所示。

图2 8号测点温度位移分量变化过程线(单位：mm)Fig.2 Temperature displacement component change process line of point 8

选取温度位移计算日之前的某几个特征时段内的气温平均温度做因子。根据东江拱坝变形统计分析的经验，参考不同测点的实测坝温与气温过程线的滞后情况，选取观测日前1、5、15、30、60、100天共6个特征时段的平均气温作为温度预报因子，特征气温因子是相对于位移计算基准日对应特征气温的增量。根据公式(5)采用多元回归方法与理论计算所得之温度位移过程进行线性拟合，所得计算结果如下：

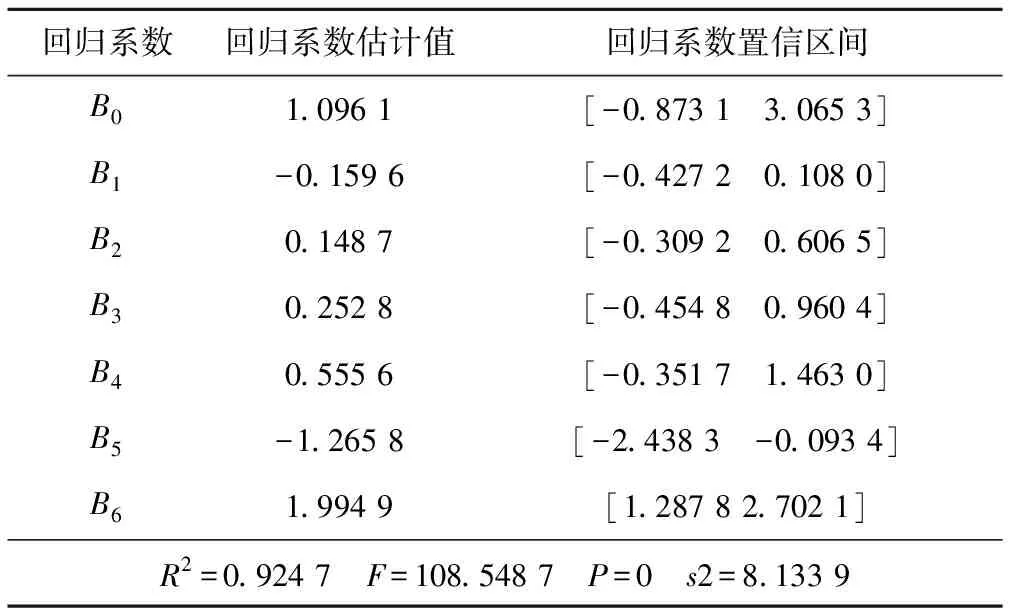
表3 温度位移分量回归系数Tab.3 Temperature displacement component regression coefficient

其中相关系数R2=0.924 7接近于1，统计量F=108.5487，与统计量F对应的概率P=0，小于显著性水平 ，说明回归在 水平上显著，回归方程有效。则温度位移分量的回归模型为：

δT=1.096 1-0.159 6T1+0.148 7T5+0.252 8T15+

0.555 6T30-1.265 8T60+1.994 9t100

(20)

式中：T1、T5、T15、T30、T60、T100分别表示观测日前1、5、15、30、60、100 d 6个特征时段的平均气温。由表3中发现，B5的置信区间不包含零点，这说明对于东江拱坝而言，在考虑拱坝的气温滞后效应计算坝体温度场时，计算日前100 d的气温平均值对于坝体温度场有较大影响。同时也说明用气温变化近似代替环境温度变化对大坝的影响是可行的。

3.3 水压位移分量计算结果

通过有限元数值分析方法计算东江拱坝在静水压力荷载作用下坝体位移。11号坝段前方交会8号测点在2003年2月-2012年12月时段内的水压位移分量变化过程线如图3所示。

图3 8号测点水压位移分量变化过程线(单位：mm)Fig.3 Hydraulic displacement component change process line of point 8

由前文所述，水位位移分量是由于坝体或基岩在库水位作用下产生的弹性变形所引起的，水荷载一经加上，变形便立即产生，因此不考虑位移对库水位的滞后，而取位移观测当天的日平均水位进行计算。根据东江大坝变形统计分析经验，取坝体水平位移为水位的4次多项式函数。根据公式(4)采用线性回归分析方法得8号测点对应部位的计算水压水平位移与坝前水深的拟合结果如表4。

表4 水压位移分量回归系数Tab.4 Hydraulic displacement component regression coefficient

表4中SSE是拟合误差的平方和，SSE=3.00说明本次拟合结果比较准确。R-square代表实测数据与拟合模型计算的数据之间相关系数的平方值，它越接近1，说明模型能更好地解释变量间的比例关系。R-square=0.998 4说明本次拟合的两组数据的相关性很好。RMSE是均方差，RMSE=0.223 8近于0说明本次拟合结果比较好，即回归模型成立。其中相关系数R2=0.999 9接近于1，统计量F=5.147 9，与统计量F对应的概率P=0，小于显著性水平 ，说明回归在α水平上显著，回归方程有效。

水压位移分量的回归模型为：

δH=-0.272 5-0.968 3H-0.013H2-1.86e-04H3-

7.585e-06H4

(21)

式中：H为计算坝前水位。

由表4可知，回归模型系数的置信区间都不包含零点，这说明该影响因子对于模型因变量的影响显著。

3.4 位移监控模型的建立

由前文计算得到温度位移分量以及水压位移分量确定性模型中的待定系数，即Ai与Bj。然后根据东江大坝1/3拱坝处8号前方交会测点在2003年2月-2013年12月位移实测数据，采用数学回归分析方法计算出公式(6)中的时效位移分量系数C1、C2以及公式(7)中的调整系数X、Y，得到东江大坝的位移确定性模型为：

δ=1.090 1δH+1.042 7δT+0.458 5lnθ-0.000 3θ-0.105 2

(22)

模型的复相关系数R2=0.916，统计量F=262.5，与统计量F对应的概率P接近于0，小于显著性水平α=0.05，说明回归计算值在α水平上显著，回归方程有效，此模型成立。

当不考虑时效位移时，测点总位移δ′为温度位移分量(δH)以及水压位移分量(δT)之和，即：

δ′=δH+δT

(23)

式(22)是利用东江大坝前方交会8号测点基于2003年2月-2012年12月的实测资料所建立的位移确定性监控模型。为了校验此位移确定性模型精度，将东江大坝2003年2月-2013年12月的实测气温及水位代入模型，得到一组位移计算值，其为模型拟合预测值，其中2003年2月-2012年12月时段的位移计算值为模型拟合值，2012年12月-2013年12月时段的位移计算值为模型预测值。图4为11#坝段8号测点位移实测值、模型拟合预测值与不考虑时效拟合值的对比图。从图中可以看出，确定性模型的拟合精度及预测精度较好，能满足工程精度要求，证明本文所述建立确定性模型的方法可行。同时，图4表明，对于长期运行的混凝土拱坝而言，不考虑时效的计算位移与位移实测值相差很小，证明时效位移在拱坝总位移中所占比例很小，几乎可忽略不计。

图4 8号测点位移实测值与模型拟合值、预测值对比图Fig.4 Displacement contrast diagram of measured values and model fitting values and predicted values of point 8

4 结 论

(1)本文采用坝区气温资料构造温度位移分量，提出以短时间序列实测资料来检验混凝土拱坝温度场的新方法，能较好的消除估算混凝土拱坝温度边界条件对混凝土确定性模型的影响，这对于大坝监控是非常重要的。

(2)针对运行期混凝土拱坝的变形特点，采用三维有限元数值分析方法计算混凝土拱坝位移的水压位移分量和温度位移分量，建立混凝土拱坝位移的确定性模型。此位移确定性模型可以实现对水压、温度及时效位移分量的分离，其精度与预测监控性能较好，为我国大部分缺乏坝体温度监测资料的运行期混凝土拱坝的安全监控提供了一个新的思路。

(3)对于运行多年的混凝土拱坝而言，时效位移分量相对于总位移所占比例很小，有时可以忽略不计，因此建立位移确定性模型时可不必包含时效分量，将时效分量和残差放在一起与模型分开研究。