基于偏秩相关-逐步回归法的SWMM模型全局敏感性分析

李传奇，崔佳伟，孙 策，段明印，马梦蝶，杨幸子

(山东大学土建与水利学院，山东 济南 250061)

0 引 言

近几年，随着我国经济社会的发展、气候的变化以及城市化和工业化的快速推进，导致城市'热岛效应'不断加重和下垫面条件发生变化，造成城市洪涝灾害频繁发生，人民的生命财产安全受到了严重的威胁[1]。利用水文模型可以有效地模拟城市洪涝过程，对城市洪水进行预报预警和管理，降低甚至避免城市洪水带来的危害[2]。SWMM模型是由美国环保署研究开发的一种暴雨洪水管理模型，能够动态的模拟研究区域内的各种水文过程，包括降雨-径流、地下水与排水管道的水量交换、污染物运移和地面积水等，在国内用来管理城市洪水已经得到了广泛的认可和使用[3]。

与大多数的水文模型类似，SWMM模型由于其众多的相关参数，在进行模型率定时工作量大、费时费力，而且不能保证每一个参数的精度[4]。这时我们就需要对SWMM模型的相关参数进行敏感性分析，得到各个参数的敏感性即对于模型输出的影响程度，对于那些敏感性小的参数，在进行参数率定时可以取其经验值进行固定，高效快速地完成参数率定，提高模型的可靠性和稳定性[5]。一般敏感性分析方法有两种，分别是局部敏感性分析和全局敏感性分析[6]。局部敏感性分析是固定其他参数不变，在取值范围内对研究参数选取一系列的值带入模型得到一系列的输出再进行分析，这种方法没能考虑到参数之间的交互作用对模型输出的贡献；全局敏感性分析通过全部参数在取值范围内的随机抽样形成一系列的输入数组带入模型得到一系列的输出再进行分析，这种方法考虑了参数之间的联合效应对输出的影响，结果稳定可靠，能够更加全方位的分析参数敏感性[7]。目前，常用的敏感性分析方法有基于修正的Morris筛选法[8]、互信息法[9]、偏相关法[10]、基于Sobol的指数法[11]、逐步回归法[12]和偏秩相关法[13]等。其中，逐步回归法和偏秩相关法都是全局敏感性分析方法，对参数的概率分布无特殊要求，适合SWMM这种参数众多而且非线性的模型。

本文以山东大学千佛山校区为例，运用SWMM模型分析降雨时该校区的水文过程，针对该模型运行时的输入参数，采用拉丁超立方对其在取值范围内进行随机抽样，利用逐步回归法和偏秩相关法对参数的敏感性进行分析和量化，为模型进一步的高效率定和不确定性分析提高参考和指导，进一步提高模型的精度和可靠性。

1 材料与方法

1.1 SWMM模型及参数

SWMM模型自从被开发以来就被全世界的科学研究人员用来研究模拟雨洪，主要包括水文模块和水质模块，应用范围广泛，特别是城市区域内降雨条件下的各种水文过程，管渠以及下水道中的水流流动等。在对山东大学千佛山校区进行模拟时，主要水文过程有管道输、排水和地表径流两个方面，求解方法为非线性水库模型和圣维南方程。

SWMM模型的相关水力水文参数共计14个，这其中管道的长度和不透水区域面积比率一般为研究区域的固定值，目前可以通过GIS、RS、DEM或者直接测量得到固定数值且误差不大，对其值进行大幅度的变化毫无意义，则只对其余12个参数进行敏感性分析。其中汇水区的坡度、面积和宽度3个参数由于其空间特性和测量时存在不可避免的误差，定义3个修正因子Pct-Area、K-With、和K-Slope来概化这3个参数[14]。通过查找用户手册和相关文献以及研究区域的实地情形，得出各个研究参数的取值范围见表1。

表1 SWMM模型各研究参数取值范围及意义

1.2 逐步回归法

逐步回归法是一种利用最小二乘法建立因变量与自变量的多元线性回归方程，再求解回归系数的方法，假设因变量为Y,则它与一系列自变量X1,X2,…,Xn之间的回归方程可以表述如下：

y=a0+a1X1+a2x2+…+anXn+ε

(1)

式中：y为因变量Y的回归值；a0,a1,a2,…,an为各个自变量所对应的回归系数；ε为误差项，表示除了自变量以外的因素对因变量Y回归值的影响。

在式(1)中，不是所有的自变量X1,X2,…,Xn都对因变量 有显著的贡献，如果能将影响程度不明显的自变量从回归方程中去掉，不但能减少计算量还能提高回归方程的预测水平，这时就可以利用逐步回归法，原理是：将自变量X1,X2,…,Xn一个一个逐步引入到回归方程中，具体的做法是该变量通过了给定偏 统计量显著性检验的情况下引入方程，此时便计算方程中所有存在的自变量的偏回归平方和，并进行排序，对偏回归平方和最下的自变量在进行显著性检验，如果不显著则从回归方程中去除，这样直到没有新的自变量引入和老的自变量去除，得到一个新的回归方程。此时每一次回归分析的R2代表引入的该自变量对于回归方程的解释程度，标准回归系数SRC的绝对值大小表示参数的敏感性程度，正、负符号表示该自变量与因变量的正、负相关关系[15]。

1.3 偏秩相关法

偏秩相关法是一种利用'等级位差'来进行分析的全局敏感性分析方法，适用条件为各参数有相同维度的随机变化。首先要计算各参数的秩相关系数，通过抽样方法生成 维自变量 ，带入模型得到 维输出变量 ,则组成的输入、输出变量矩阵如(2)所示。

(2)

变量Y,X1,X2,X3,…,Xn中，任意两个变量之间的秩相关系数为:

(3)

式中：Ri为n维变量Y/Xk中第i个变量的秩(该变量在 维变量从大到小排序后所在的位次)；Qi为n维变量Xm中第i个变量的秩。则得到这些输入、输出变量间的秩相关系数矩阵P和P的逆矩阵C为：

(4)

(5)

式中：偏秩相关系数|PXi|的值越大，说明该参数的敏感性越大即对模型输出的影响程度，PXi的符号代表该参数与输出变量之间的正、负相关关系[16]。

1.4 抽样方法

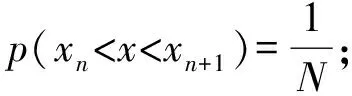
1.5 研究区域概况

山东大学千佛山校区南苑位于山东省济南市历下区，总面积为79 887.53 m2，是季风气候明显区域之一。寒冷晴朗，雨雪稀少，多偏北风。夏季受热带、副热带海洋气团影响，盛行来自海洋的暖湿气流，天气炎热，雨量充沛，光照充足，多偏南风。春季和秋季是冬季转夏季、夏季转冬季的过渡季节，风向多变；年平均降水量672.7 mm，其中7、8月份最多，占全年的55%以上，三面环山的地理情况让热空气无法扩散，使得区域内夏季高温湿热。该研究区域由于特殊的地形关系，无其他径流流入，是一片相对独立的区域。其中，不透水区域包括混凝土地面、屋顶和运动场地(混凝土和塑胶)，透水区域包括花坛、草坪等绿地，土地利用情况见图1。

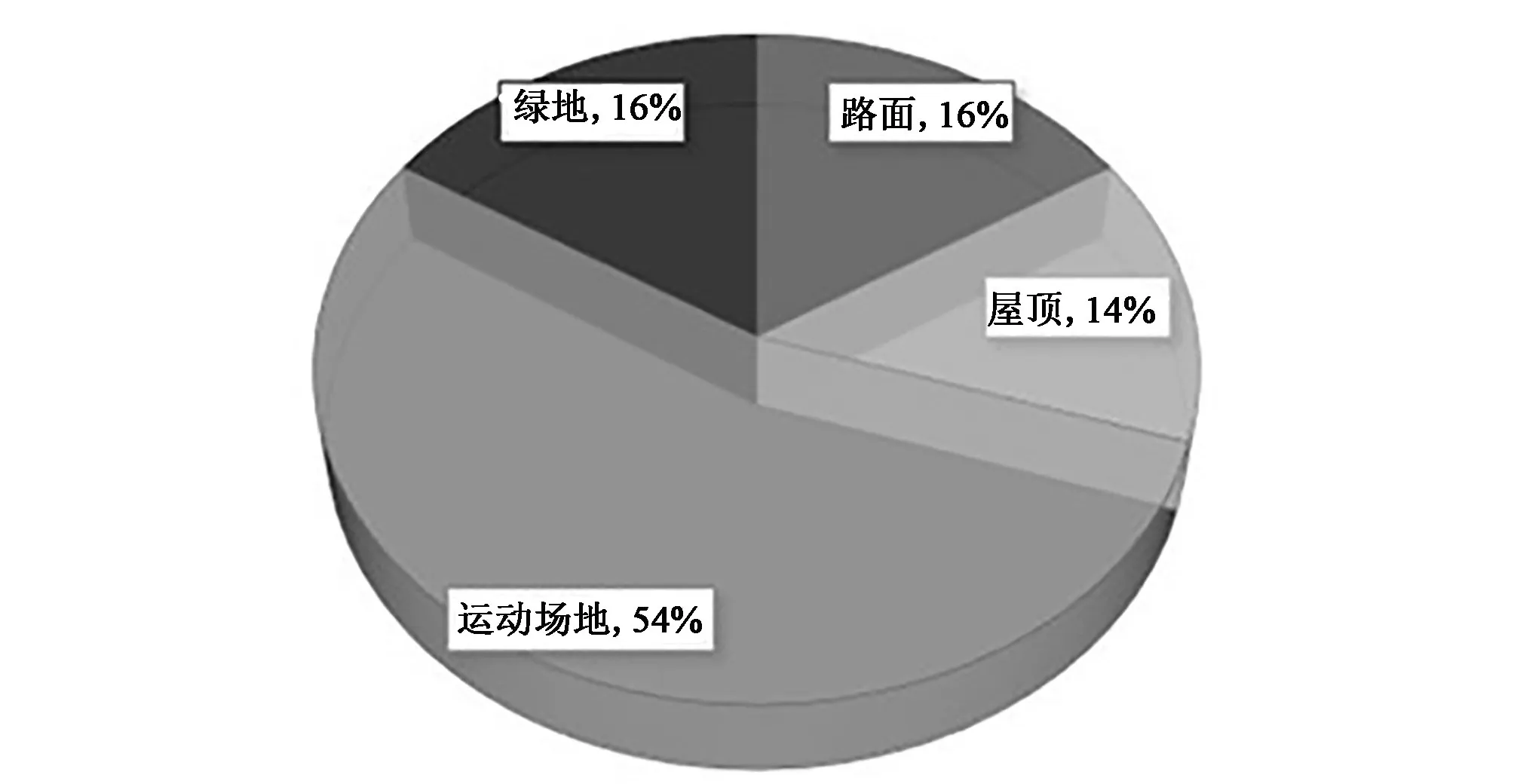
图1 千佛山校区南院土地利用情况

对研究区域进行SWMM模型数字概化，其中子汇水区域24个，节点23个，9条为地下管线，14条为道路，3个雨水排放口。该研究区域的概化图见图2。可以看出，该研究区域四季分明，降雨量充沛且土地利用类型覆盖完整、子汇水区域复杂，对于季风气候下区域的SWMM雨洪模型具有一定的代表性。

图2 研究区域概化图

1.6 设计降雨

本研究的设计降雨计算基于最新的济南市降雨强度计算公式，我国降雨中双峰雨型和多峰雨型较少，大多为单峰雨型，并且大部分地区的雨峰系数在0.3～0.5之间，这种情况与芝加哥雨型非常相似。由此本研究利用芝加哥降雨模型推求降雨过程线具有一定的代表性，得到的设计降雨重现期为1 a，降雨量52.76 mm，降雨强度时间间隔为2 min，雨峰系数为0.4。设计降雨过程线如图2所示，济南降雨强度计算公式如(6)。

(6)

式中：q表示降雨强度即每分钟的降雨量，mm/min；P表示降雨重现期，a；t表示降雨历时，min。

图3 研究区域设计降雨过程线

2 结果与分析

利用matlab程序实现拉丁超立方抽样，需要将SWMM模型的12个研究参数取值范围的上限和下限分别带入程序计算得到1 000组输入变量组合，再通过matlab的for循环语句写入SWMM开源的输入文件，最后将1 000个输入文件依次代入模型进行计算得到3个1 000组重要的水文输出变量：总产流量、峰值流量和峰值时间。之后，再将输入、输出变量组成3个 的矩阵，应用逐步回归法和偏秩相关法对其进行全局敏感性分析。

2.1 逐步回归法分析

利用matlab实现逐步回归法的基本程序，之后对输入、输出的变量矩阵的进行敏感性分析，结果如表2所示。对于峰值流量来说，N-Imperv和k-Width的|SRC|值相差无几，稍大于其他参数，且引入这两个参数时，R2的增量也相差无几，但整体上来看，N-Imperv的敏感性要稍大于K-Width；在引入所有参数后，R2的值达到了0.929，说明峰值流量与各个参数之间的线性相关关系很好。对于峰值时间来说，N-Imperv的|SRC|值和引入方程时R2的增量都大于其他的参数，是对峰值时间最敏感、起决定性作用的参数，并且是正相关关系；在引入所有参数后，R2的值达到了0.884，说明峰值时间与各个参数之间的线性相关关系很好，其中，剔除了S-Perv、Max.Infil.Rate和Min.Infil.Rate这3个不敏感参数。对于总产流来说，Per-Area的|SRC|值和引入方程时R2的增量都大于其他的参数，是对总产流最敏感、起决定性作用的参数，并且是正相关关系；在引入所有参数后，R2的值达到了0.952，说明总产流与各个参数之间的线性相关关系很好，其中，剔除了N-Imperv和Manning-N这两个不敏感参数。

表2 逐步回归法分析结果

同时，不透水区的曼宁系数N-Imperv对于排放口的峰值流量和时间都是最敏感的参数、但是对于总产流来说却是不敏感的参数，分析可知，N-Imperv只会影响水流在不透水地面上的流动状态，并不会影响水流的总量。这个结果也间接说明了逐步回归法分析的准确性。

2.2 偏秩相关法分析

利用matlab程序实现偏秩相关法的基本程序，之后将1 000 组SWMM模型的输入、输出数据带入程序进行敏感性分析，得到如表3所示的分析结果。对于峰值流量来说，N-Imperv是最敏感的参数，偏秩相关系数P的值达到了-0.864，与峰值流量有较高的负线性相关关系；K-Width是第二敏感的参数，P值为0.853，与峰值流量有较高的正线性相关关系；是因为这两个参数会影响水流在研究区域内的蓄、流状态，从而影响了峰值流量。对于峰值时间来说，N-Imperv和K-Width是敏感性排名前两位的参数，P值分别达到了0.926和-0.822，与峰值时间有较高的正线性相关和负线性相关关系，同时也都通过影响水流在研究区域内的蓄、流状态，从而影响了峰值时间。对于总产流来说，最敏感的参数为Pct-Area，P值达到了0.919，与总产流有较高的正线性相关关系，这是因为，子汇水区面积比例因子的增大会增加计算降雨量，从而增大了总产流量。

表3 偏秩相关法分析结果

2.3 结果对比分析

将两种敏感性分析方法结果画在同一个柱状图里进行对比，见图4、5、6。可以发现，对于峰值流量来说，两种方法得到的最敏感的两个参数都是N-Imperv和K-Width，并且所有参数的敏感性排序和正、负相关关系都相同；对于峰值时间来说，两种方法得到的最敏感参数都是N-Imperv，逐步回归法剔除了S-Perv、Max.Infil.Rate和Min.Infil.Rate 3个参数，在偏秩相关法里，这3个参数P值很小也是最不敏感的参数，并且其他参数的敏感性排序和正、负相关关系都相同；对于总产流来说，两种方法得到的最敏感参数都是Pct-Area，逐步回归法剔除了N-Imperv和Manning-N这两个参数，在偏秩相关法里，这2个参数P值很小也是最不敏感的参数，并且其他参数的敏感性排序和正、负相关关系都相同。

图4 峰值流量分析结果对比

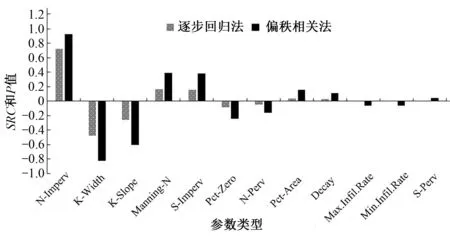
图5 峰值时间分析结果对比

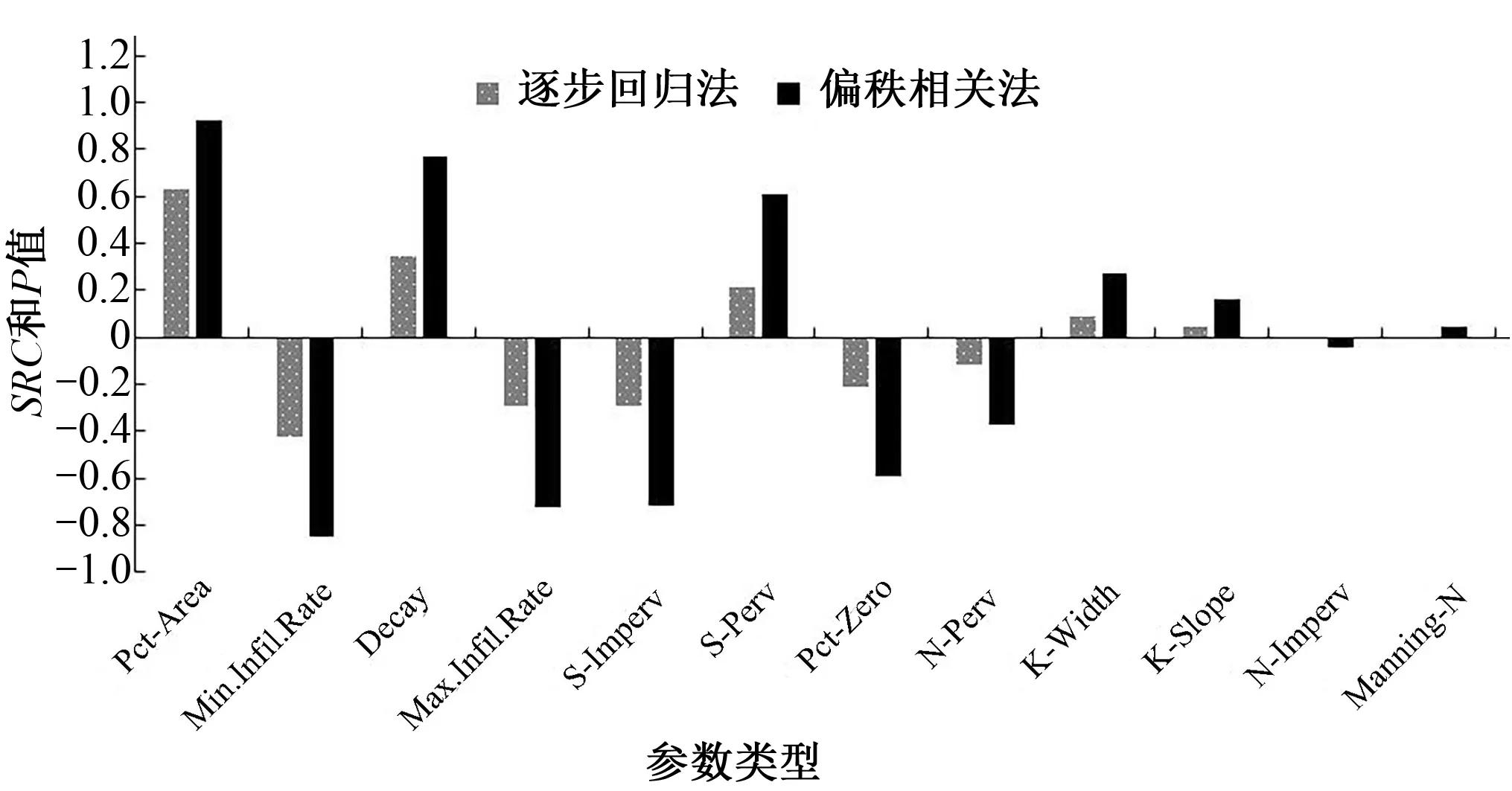
图6 总产流分析结果对比

3 结 语

(1)研究参数的输入组合达到1000组，拉丁超立方的抽样方法也保证了随机抽样的数据能均匀分布在取值范围内，数据具有一定的代表性，且逐步回归法和偏秩相关法都是线性分析方法，两种方法得出的结论完全相同，更说明了结论的合理性和可靠性以及SWMM模型建立的准确性。

(2)通过两种分析方法得知：N-Imperv是对峰值流量敏感性最大的参数，且它们之间是负相关关系，两种方法得到的各个参数的敏感性排序相同；N-Imperv是对峰值时间敏感性最大的参数，随着N-Imperv的增大峰值时间也会越来越长，两种方法得到的各个参数的敏感性排序相同，并且敏感性最小的3个参数都是S-Perv、Max.Infil.Rate和Min.Infil.Rate，在进行模型率定时可以取固定值；Pct-Area是对总产流最为敏感的参数，与总产流呈正相关关系，两种方法得到的各个参数的敏感性排序相同，并且敏感性最小的两个参数都是N-Imperv和Manning-N。

(3)通过敏感性分析，精确识别了SWMM模型的敏感因素，为接下来不确定性分析和模型率定提供了 参考和指导，减少建模的工作量，提高模型率定的效率。