导叶时序效应对液力透平性能影响的研究

2019-01-21柴立平张舜鑫潘凤建

中国农村水利水电 2019年1期

柴立平，张舜鑫，陈亮，潘凤建

(1.合肥工业大学，安徽合肥 230009；2.安徽省科学技术研究院，安徽合肥 230031；3.安徽南方化工泵业有限公司，安徽泾县 242000)

0 引言

导叶广泛应用于泵和压缩机等方面，其形成了一种非常重要的流通通道。导叶可以用在单级离心泵中来减少径向力，也可以应用于多级泵中将液体的动能转换为压力能。然而，一些复杂的流动特性，如不稳定交互是由于转子和定子之间的相对运动而产生的，这些流动特性对泵的外特性有很大的影响。不稳定的交互作用产生高压脉动可以引起不稳定的动态力，动态力引起振动并对泵造成损害。

时序效应即改变叶栅(动叶与动叶或静叶与静叶)之间周向相对位置对叶轮机械机组性能的影响。时序效应研究最早源自于涡轮机械，近年来国内外学者对涡轮、压缩机等导叶时序效应做了大量研究，也有学者对单级离心泵导叶时序效应做了研究。ARNONE等[1]采用标准三维方法研究了时序效应对低压透平及非定常流动的影响，对静叶进口边的非定常压力分析，指出了最优时序位置。BOHN等[2]采用数值模拟方法对一两级轴流透平的第二个静叶时序位置进行了优化，得到了一个效率最高的静叶时序位置。还有学者对离心泵内部的时序效应进行了研究，并对一些特定的离心泵的叶轮和导叶的时序布置给出了一些建议[3-7]。也有学者采用数值模拟和试验结合对比的方法，研究了叶轮参数和时序效应对导叶式离心泵内非定常压力脉动的影响，得出导叶时序对叶轮与导叶的动静干涉引起的压力脉动强度较为明显，并指出了导叶最佳参考安装位置[8-10]。杨军虎等[11-12]采用数值计算的方法研究了导叶形状和导叶数对液力透平压力脉动的影响，得出了在特定透平上压力脉动幅值最小的导叶形状和导叶数。还有学者对影响液力透平压力脉动的因素也进行过一些探讨[13,14]。

目前，对于透平的研究多集中在叶轮与导叶上。然而，对于导叶的研究几乎都集中在螺旋形蜗壳的单级离心泵反转透平上，对于环形蜗壳多级离心泵反转式液力透平的研究较少。而多级离心泵反转式液力透平回收的能量更大，回收功率范围更宽。随着能量回收上限的提升，对多级离心泵反转式液力透平的需求将会越来越大，所以，对于多级离心泵反转式液力透平内部流动与振动稳定性的研究很有必要。为简化计算模型，本文以多级透平的首级为研究对象，采用计算流体力学(CFD)方法研究了0.4Qd、0.6Qd、0.8Qd、1.0Qd、1.2Qd5个流量工况下导叶在一个栅距内4个不同时序位置对透平外特性和内部压力脉动强度的影响，为透平导叶最优时序位置提供参考。

1 数值计算

1.1 透平模型参数

本文采用的透平模型为相似换算模型，以原石油化工加氢裂化能量回收液力透平[15]为原型，经过缩小化换算及重新水力设计修正，所得的单级模型泵参数和主要几何特征如表1所示。其结构为单级导叶式离心泵，带径向导叶，蜗壳形式为环形中出式。多级泵反转做透平的首级几何模型如图1所示。

1.2 网格划分与数值模拟设置

采用ICEM软件对透平模型水体进行非结构网格划分。并对数值模拟进行网格无关性检查，如图3所示，最终确定网格数约为440万个。为避免进出口边界条件对结果产生影响，对进出口进行了延长。

利用商业软件CFX 16.0在5个不同流量工况下对导叶不同时序位置进行三维定常和非定常数值模拟，采用标准k-ε湍流模型求解定常和非定常雷诺时均方程，边界条件设置为总压进口和质量流量出口，参考压力设置为0 Pa，壁面选择边界无滑移条件，且动静交接面选用MRF多重参考系，网格连接方式选择GGI方式。

表1 单级模型泵主要设计参数Tab.1 Main design parameters of single-stage centrifugal pump

图1 透平首级模型水体图Fig.1 Water body diagram of the first turbine model

图2 计算域网格划分Fig.2 Calculates the domain grid division

图3 网格无关性曲线Fig.3 Grid independence curve

1.3 建立导叶时序位置

以叶轮旋转轴为原点，建立如图4所示的Oxy直角坐标系，定义导叶A叶片背面出口边与x轴的夹角θ为导叶与蜗壳不同的相对时序位置，定义θ=90°为时序位置C1，即图4所示的导叶位置，逆时针将导叶旋转10°为下一个时序位置，当θ=120°时为时序位置C4。

1.4 应用公式

对于模型泵工况及透平工况的外特性研究分析，主要以水头、效率、回收功率这几个参数来分析。对于上述参数的方程如下所示。

水头：

(1)

式中：Pout为透平出口总压，Pa；Pin为透平进口总压，Pa；ρ为透平输送液体的密度，kg/m3；g为重力加速度，m/s2。

功率：Pf=HQmg=ρgQH

P=Mn/9 550

(3)

式中：Pf是透平的流体功率，W；Qm为透平的质量流量，kg/s；Q为透平的体积流量，m3/s;P是透平的回收功率，kW；M为透平的扭矩，N·m；n为透平的转速，r/min。

透平效率：

η=P/Pf

(4)

透平内部流动为大雷诺数紊流，因此，仿真湍流模型采用标准的k-ε模型。

2 透平外特性和内流场分析

为了研究不同导叶时序位置对透平外特性和内部流场的影响，对该单级泵反转做透平时在4个不同时序位置的计算模型分别取五个同流量工况下进行定常数值计算。经数值模拟计算得出该透平的最优效率点的流量为40 m3/h,因此取该流量为透平的额定流量(1.0Qd),并分别取该额定流量的0.4Qd、0.6Qd、0.8Qd、1.0Qd、1.2Qd进行计算。

图5为4个不同导叶时序位置下，模型透平工况的外特性曲线。由图可知，该透平的效率随着流量的增加而增大，当流量增至40 m3/h透平的效率达到最大，流量继续增加透平效率开始下降。在最高效率点处C3的效率最高，其次为C1、C4、C2。透平的水头是随着流量的增加持续增大的，且在导叶时序位于C3位置时，透平消耗的水头也是最大的，其次为C1、C2、C4。

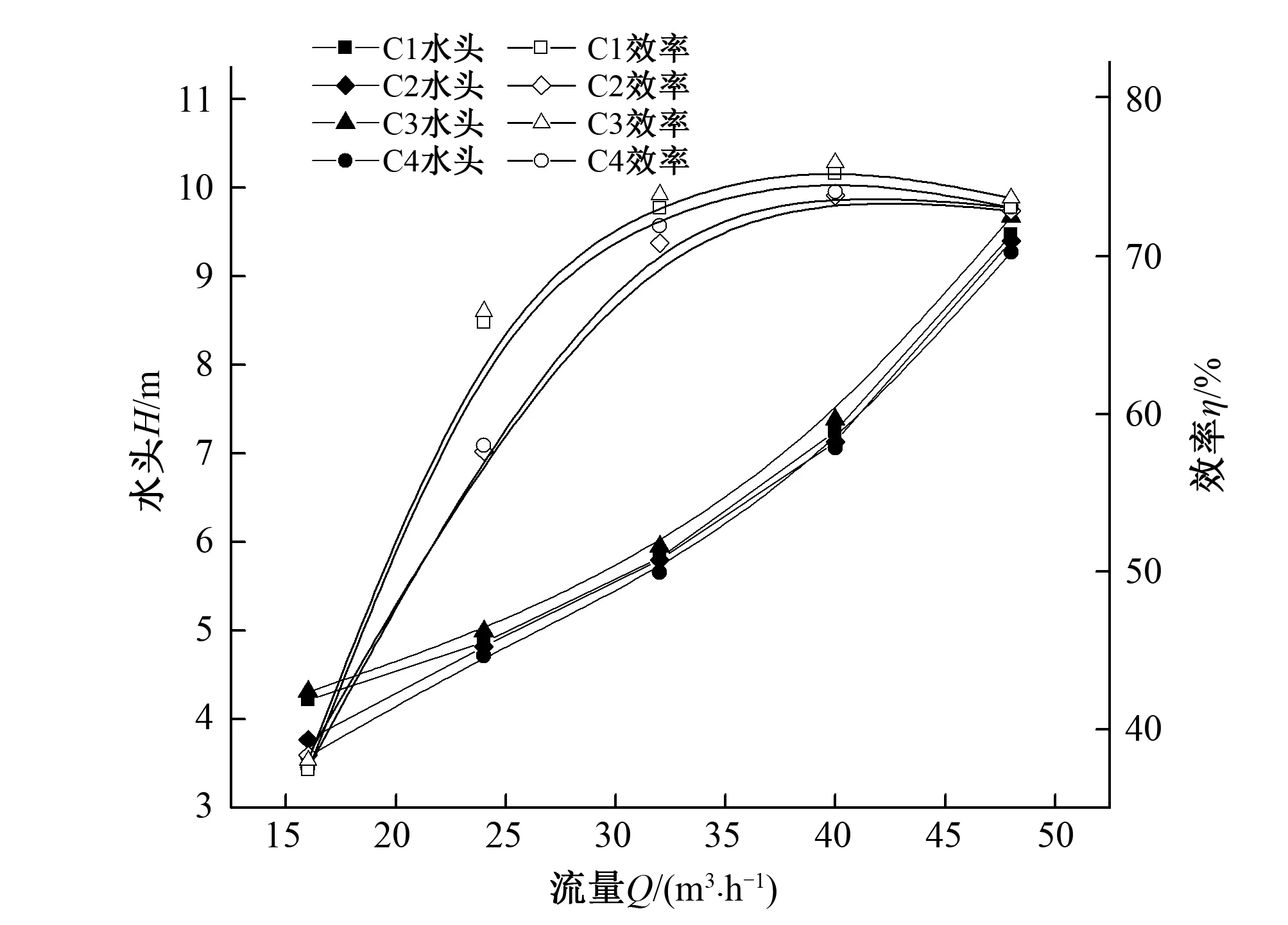
图5 不同导叶时序位置计算模型的透平外特性曲线Fig.5 The curves of turbine characteristics of different guide vane timing sequence position calculation models

图6为4个不同导叶时序位置下模型的回收功率曲线。由图可知在透平回收功率是随着流量的增加而逐渐增大的，且在C3时序位置时的回收功率是最大的。

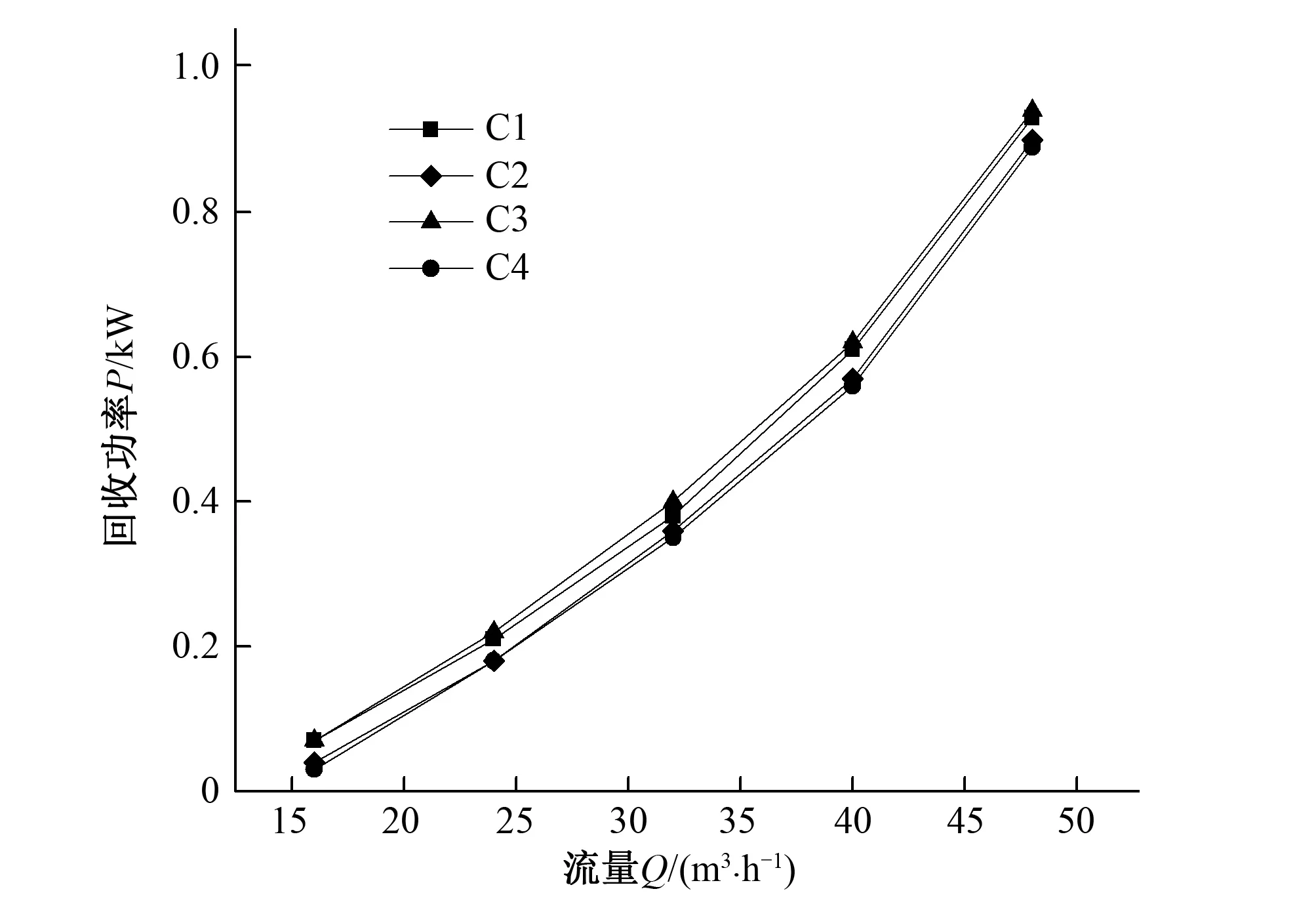
图6 不同导叶时序位置透平回收功率曲线Fig.6 Turbine recovery power curves of different guide vane timing sequence positions

由于各时序位置在最高效率点处的外特性参数差异较小，特列出表2在最佳效率工况下各时序位置透平的外特性参数。由表2可知在流量为40 m3/h时，透平在时序位置C3处的水头是最大的，比最小的C4高0.32 m；在时序C3处的效率也是最高的，比最低的C2效率高2.08%；在时序C3处的回收功率也是最高的，比最小的C4回收功率高0.06 kW。

图7为4个不同导叶时序位置下，模型在流量为40 m3/h时透平工况的叶轮中截面流线图，由于C3导叶时序位置处θ为110°，相邻两个导叶叶片的中心和蜗壳进口中心面重合，所以在蜗壳进口的高压液流对导叶叶片冲击较小，所以从图7中可以看出内部流动较均匀平稳，且在导叶入口没有旋涡产生。而导叶时序位置位于C1时，其参考导叶叶片A正好对准蜗壳进口中心，透平进口液流对导叶叶片A有冲击现象，所以在导叶的入口处有较小的漩涡产生，但由于叶片正好处于蜗壳进口中心位置，透平进口液流从蜗壳中心两侧均匀进入导叶，所以由冲击引起的旋涡还是较小的。而当导叶时序位置位于C2与C4时，其导叶叶片斜置于蜗壳进口，蜗壳进口中心面两侧入流不均匀且与导叶叶片发生冲击，所以其入口处产生漩涡较多，且漩涡较大。从流线上看，当透平的引水结构为环形蜗壳时，水流在蜗壳入口处被分为两部分，如图7所示，右侧部分水流速度方向与导叶叶片弯曲方向相同，而左侧部分则相反，造成蜗壳及导叶左侧部分流动不如右侧部分平稳。

表2 透平在最佳效率工况下各时序位置的外特性参数Tab.2 The external characteristic parameters of each time series position of turbine under optimal efficiency condition

图7 模型透平叶轮中间截面流线图Fig.7 Model turbine impeller middle section flow chart

图8为4个不同导叶时序位置下，模型在流量为40 m3/h时透平工况的叶轮中间截面速度云图，由图可知，当导叶处于C1和C3时序位置时，透平蜗壳内左侧和右侧液流速度相差不大，在蜗壳底部低速区较小，左右两股液流发生的冲击损失也相对较小，其中C3略好于C1；而导叶位于C2和C4时序位置时，透平蜗壳内左侧和右侧液流速度相差较大，右侧明显大于左侧，左侧蜗壳流动较为混乱，且在蜗壳底部低速区较大，左右两股液流冲击损失也相对较大。

图9为4个不同导叶时序位置下，模型在流量为40 m3/h时透平工况的叶轮内部压力云图，当导叶处于C2时序位置时，叶轮中间流面上静压最大为401 700 Pa，C4、C1、C3叶轮中间流面上的静压依次减小，且C2时序位置处叶轮内部的最大静压比C3时序位置的高16 000 Pa。由图5透平外特性曲线可知，在流量为40 m3/h工况下，C3时序位置的透平能量回收效率最高，那么在同等透平压力进口条件下，其叶轮内的静压必定小于其他时导叶时序工况，这也与图9所得到的叶轮内部压力云图相一致。

图9 模型透平叶轮内部压力云图Fig.9 Model turbine impeller internal pressure cloud

3 透平压力脉动分析

3.1 监测点布置及计算设置

透平内部的压力脉动是造成透平装置振动的主要因素之一，而透平内部的压力脉动主要是由透平过流部件之间的动静干涉产生的。为了研究不同的导叶时序位置对透平内部压力脉动的影响，分别在不同导叶时序位置下的模型内部布置压力监测点，并对透平模型在额定流量下(40 m3/h)进行非定常数值计算。压力监测点的布置方式如图10所示，导叶的压力监测点布置在导叶出口流面中部，图示为时序位置C1处的布置情况，其他导叶时序的监测点布置方式一致。在蜗壳进口同一垂直高度处布置一个监测点，其余监测点间隔45°均布于截面中间同心圆处。导叶与蜗壳所有监测点均布置于同一个平面内，此平面为叶轮的中截面。非定常的初始计算条件为定常计算结果文件，总计算时长为0.36 s，为6个叶轮旋转周期时长，时间步长为0.000 5 s，每一个叶轮旋转周期有120个时间步长。选取最后一个旋转周期的计算结果进行分析。

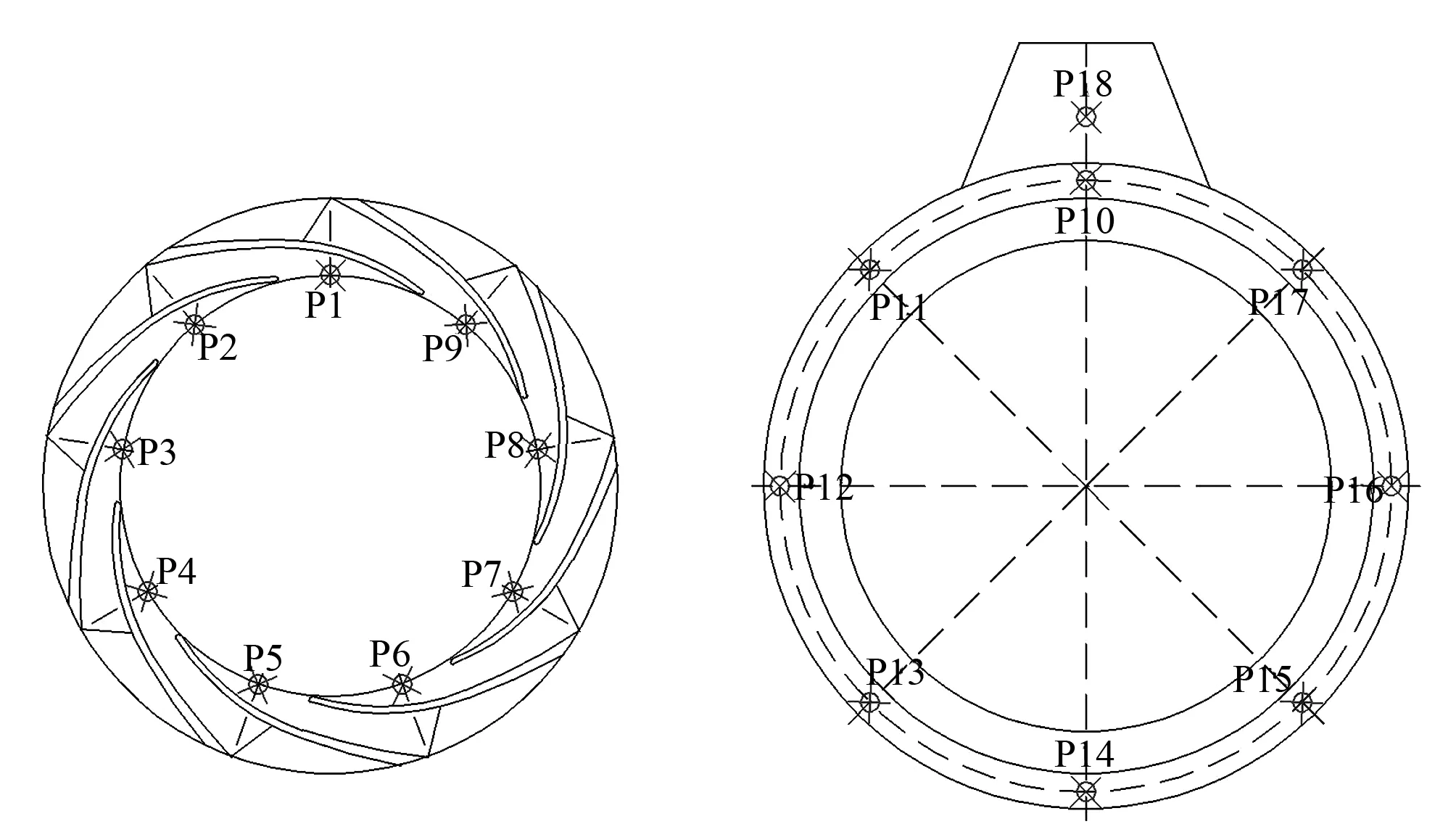
图10 透平内压力监测点布置示意图Fig.10 Layout of pressure monitoring points in turbine

为了消除静压对结果分析的干扰，引入压力系数Cp进行结果分析。Cp表达式如下：

(5)

3.2 结果分析

经数值计算得出透平蜗壳进口处监测点的压力脉动情况较其他监测点更为显著，所以分别选取导叶和蜗壳内的监测点P1和P10进行压力脉动分析。图11、12为4种导叶时序下，模型在额定透平工况的导叶内部监测点P1处的压力脉动时域图及频域图。由于导叶时序的变化导致无法在导叶内相同的位置布置监测点，所以选取各自最能代表整体压力脉动的点P1进行横向对比(相似位置)。其中，透平转频fn=N/60=16.667 Hz，叶频f=6fn=100 Hz。从时域图上可以清楚看出，C1导叶时序位置时模型的平均压力最大，但压力脉动幅值也最大，极差约为1.2 MPa，约占总水头的16%。C2和C4导叶时序位置模型的平均压力基本相等，但要小于C1导叶时序位置模型，C3导叶时序位置模型的平均压力最小，但这四种情况下的极差值基本相等。从频域图上看，C1和C3导叶时序位置下导叶的压力脉动幅值要大于其他两种情况，尤其在一倍叶频处。四种时序下的压力脉动幅值频率几乎都在叶频及叶倍频处，除1倍叶频处外，其他叶倍频下的压力脉动幅值相差不大。

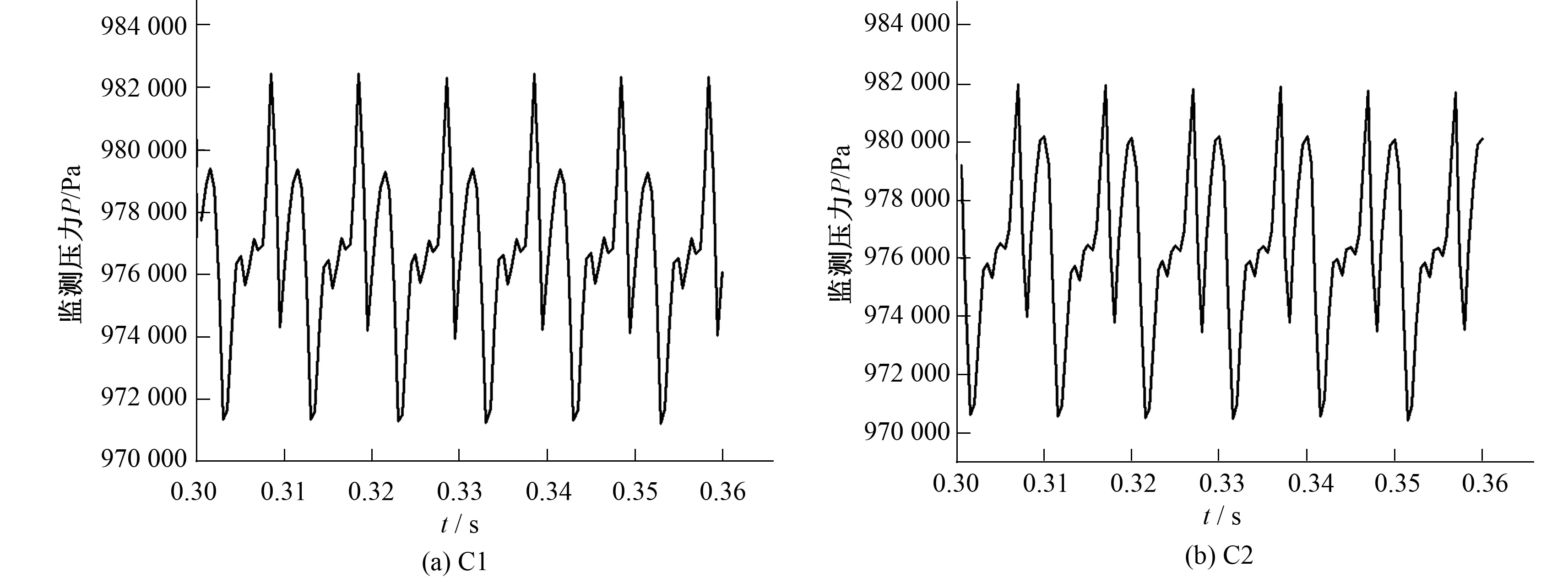
图11 导叶压力监测点P1时域图Fig.11 Time domain map of guide vane pressure monitoring points P1

图12 导叶压力监测点P1频域图Fig.12 Frequency domain map of guide vane pressure monitoring points P1

图13、14为4种导叶时序位置下，模型在额定透平工况的蜗壳内部监测点P10处的压力脉动时域图及频域图。从时域图可以看出蜗壳内部压力的总体脉动情况与导叶内部压力的脉动情况类似，但各个时序处的脉动幅度比导叶处大。从频域图上可知，蜗壳内部压力的脉动频率也均在叶频及倍频处。在1倍叶频处，C1、C2导叶时序位置模型的压力脉动幅值要远大于其他两种情况；但在2倍叶频处，C1导叶时序位置模型下的压力脉动幅值要更大；在3倍叶频处，C1、C2和C4时序位置模型的压力脉动幅值要大于C3。在蜗壳内部，比较四种导叶时序位置，总体来说压力脉动的幅值是在C1处最大，其次为C2和C4,在C3处压力脉动幅值最小。