大尺度基岩抗剪强度的有限元随机模拟与理论公式研究
2019-01-21彭俊杰赖国伟
彭俊杰,赖国伟
(武汉大学 水资源与水电工程国家重点实验室,湖北 武汉 430072)
0 引 言
在工程实践中,天然基岩一般具有庞大的体积,而人们能够用于测试其力学性质的试件往往较小,且由试验测得的力学参数呈现出很大的离散性和不均一性,其力学性质并非像确定性均质材料那样是一成不变的,而是随空间位置的变化而变化的,即使在同一地质单元内也不例外。由于岩体的强度与变形特性是工程设计中极其重要的影响因素,因此在设计中能否正确选用岩体(此处及下文中提到的“岩体”均指同一地质单元内的坝基岩体)抗剪断摩擦系数和黏聚力等力学性质参数,关系到能否确保高坝等大型水电工程的安全性和经济性。
对于目前岩土工程中的大尺度岩体的抗剪强度参数,由于缺乏具有充分理论依据的计算公式,很多情况下都是采用小尺度试块的试验结果并依赖经验与半经验的方法来确定。从国内外研究现状来看,各国对岩体抗剪强度参数的选取和整理方法并不相同,其中,具有代表性的方法主要有以下几种:
(1)日本国方法(优定斜率法)[1,2],即把试验成果整理分析严格建立在岩体质量分级基础上,并对各类岩体首先确定一个较为合理的摩擦系数f的值,然后求出相应的黏聚力c的上、下限值,并以下限值作为设计参考值。成勘院后来改进了日本人的优定斜率法,并在二滩、溪洛渡等工程中得到了应用。
(2)美国陆军工程师兵团方法[3,4],即当现场试验资料充足时,岩基设计抗剪强度可由试验σ-τ散点图的下界限确定,其中σ为试块正应力,τ为试块抗剪强度。
(3)我国方法[4],即当试验资料不足时,主要参考同类型工程的经验数据来确定;而当试验资料充足时,大多数情况是以现场试验的峰值强度的小值平均值为基础来加以确定的。
近年来,对于岩体力学参数取值选取的理论方法,有大量学者做了相关研究。比如杨强等[5]、黄志全等[6]把可靠度理论用于岩体f、c值的计算,即按给定的概率分布来估计可靠性指标,并采用均值和标准差这两个参数对设计表达式作线性处理;Karakus等[7]、Sonmez等[8]从抗剪强度参数的随机不确定性和模糊不确定性出发,推导出岩石抗剪强度参数的随机-模糊线性回归方法计算公式;王登刚等[9]提出了岩土工程位移反分析的遗传算法并应用该方法反演了弹性模量和泊松比;李辉等[10]运用了一种基于模糊支持向量机的回归方法,对岩石抗剪强度参数进行了最优估计。
上述国内外岩体力学参数的各种取值方法各有特点,但具有的共同性是都带有一定的主观性和经验性,最终的计算结果并不能真实地反映岩体的力学特性。
文献[11]中提出把大尺度岩体的抗剪强度参数称为宏观抗剪强度这一概念,并将随机场理论和现代物理学逾渗临界理论相结合起来,推导出了在小尺度材料参数服从正态分布情况下的大尺度岩体特征单元处于整体破坏的临界状态时对应的岩体宏观抗剪强度的上、下限理论计算公式。本文将在此基础上,进一步研究在小尺度材料参数分别服从正态和对数正态分布条件下的大尺度岩体宏观抗剪强度更为精确的理论计算公式,并通过弹塑性有限元与随机模拟相结合的方法来加以验证。
1 岩体力学性质的向量随机场描述
从大体积的岩体材料中任取出一个包含足够多试样般大小岩体的立方体∂V(图1),其中,把∂V定义为宏观岩体特征单元,而把试样般大小的岩体定义为小尺度岩体特征单元,相应的力学性质分别为宏观材料力学性质和小尺度材料力学性质。另外,考虑到用试块尺度去观察岩体时,表现出随空间位置变化的岩体小尺度力学性质整体上可用一向量随机场ε(r)来描述[12],忽略其他对抗剪强度研究无关或非主要的参数后,可表示为:
ε(r)=[E(r)μ(r)f(r)c(r)]T
(1)
式中:E(r)、μ(r)、f(r)、c(r)分别表示岩体的小尺度弹性模量、泊松比、摩擦系数和黏结力的随机场;r为位置矢量;T表示向量的转置。
为了简化研究,本文对位于同一地质单元内的岩体的小尺度力学性质随机场ε(r)做出了以下假设:
(1)统计均匀性:即随机场的统计特性(如均值和方差)不随空间位置的变化而变化。
(2)统计各向同性:即随机场的统计特性不随空间位置坐标系的旋转而变化。对于成层岩体这类材料,则需将本条性质改为统计横观各向同性,即随机场的统计特性在层面的各个方向上都相同。
(3)各态历经性:即设想当试件数目取得足够多时,试验所得的材料性能可历经大尺度材料内任一部位处材料性能的所有可能数值。
2 逾渗临界理论简介
逾渗这一概念最早是由Broadbent和Hammersley共同提出的[13],其本质上属于一种临界现象,可简单地用以下现象来描述。
设有一正方形格子,共有N×N格点,其中N为一条边上格点的数量。现在,格子上的每个格点均有一次机会以概率p接受(或以概率1-p拒绝)一颗棋子的占据。显然,最终将会得到一个由棋子和空格点所组成的阵型。随着p从0到1逐渐增大,格点将从没有被一个棋子占据的状态变为全部被棋子占据的状态。根据逾渗临界理论,存在这样一个临界概率pcr,当p小于pcr时,格子中的棋子呈孤立状态;而当p大于pcr时,格子上相对的两条边界可以通过一条由相邻棋子所组成的路径从而贯通[14](图2)。

图2 二维逾渗模型中p
又如,有一种可渗透的孔隙介质,当流体通过介质时,其中的孔隙会被随机堵塞,从而导致其孔隙率下降。当孔隙率下降到某一临界值时,孔隙介质就会由导通状态变为不导通状态,从渗透性的角度来讲,这属于一种相变[15]。
同样的,大尺度材料的破坏演化过程与逾渗过程十分相似,基于此理论,为本文研究大尺度岩体的宏观抗剪强度提供了可能。
3 岩体宏观屈服的临界分析
对于宏观岩体特征单元∂V,在宏观均布力的作用下,由前面小尺度力学性质随机场的假定可知,∂V内各小尺度岩体特征单元的屈服概率pf(r)为一常数p(p同时还表示∂V内所屈服的小尺度特征单元所占单元总数的比例)。随着荷载的增大,屈服概率p也随之增大。根据逾渗临界理论,存在这样的一个临界屈服概率pcr,当p
对于宏观岩体特征单元∂V的任一截面∂Aα,存在这样一种临界现象,即当p
而对于宏观岩体特征单元∂V自身,其发生整体屈服与否的临界现象与∂Aα的情况相比有很大的区别,若∂V发生了整体屈服,则其内部的非屈服的单元必然不能相连并贯通相对的两个加载面,也就是说,∂V内的非屈服单元此时并不能在两个加载面之间相连形成支撑起整个∂V的“骨架”。若只是∂V内的屈服单元相连并贯通相对的两个加载面(塑性屈服区贯通),则只能说明此时∂V发生的是局部屈服,而不是整体屈服,因为此时支撑起整个∂V的“骨架”还存在。
至于临界屈服概率pcr3d取值为多少,目前尚无精确的理论推导公式,但可以通过∂Aα所对应的逾渗模型(二维)的逾渗阈值外推出∂V所对应的逾渗模型(三维)的逾渗阈值。已知pcr2d=0.5,则此时小尺度特征单元的屈服比例为0.5,进一步可得出∂Aα所对应的逾渗模型的逾渗阈值为1/2。在此基础上,不妨推测∂V所对应的逾渗模型的逾渗阈值为1/3(以对应维数的倒数为推测依据),则此时∂V内的非屈服单元刚好不能在相对的两个加载面之间相连形成支撑起整个∂V的“骨架”的临界比例p为1/3,从而得出此时屈服单元所占比例为2/3,即临界屈服概率pcr3d=2/3。至于,外推的pcr3d是否正确,本文将通过下面的数值模拟试验来验证。
4 基于有限元随机模拟方法的岩体临界屈服条件研究
本文将采用弹塑性有限元和随机模拟相结合的方法,通过对宏观岩体特征单元∂V逐步屈服过程进行数值模拟,来研究确定∂V的临界屈服条件。
4.1 ∂V中小尺度岩体特征单元力学参数的抽样方法
用直角坐标面将∂V离散成一个个代表小尺度岩体特征单元的微元体,对于每一个微元体,其小尺度力学参数主要有E(r)、μ(r)、f(r)和c(r)。不失一般性,在本文的有限元随机模拟计算中,假定∂V中各小尺度特征单元之间的具有同一力学性质的参数是相互独立的,且暂不考虑同一小尺度特征单元f(r)和c(r)之间的相关性。则当小尺度力学参数服从正态分布时,可按以下任意两式之一进行蒙特卡罗抽样[16,17]:
(2)
(3)
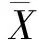
当小尺度力学参数服从对数正态分布时,可按以下任意两式之一进行蒙特卡罗抽样[16,17]:
(4)
(5)
其中:
(6)
(7)
4.2 计算机数值模拟方案与试验步骤
在弹塑性有限元数值模拟中,小尺度材料的力学模型采用理想弹塑性模型,屈服准则采用Mohr-Coulomb屈服准则,且塑性流动法则采用关联流动法则。宏观岩体特征单元∂V的加载方式为:横向围压施加宏观均布压力σ2、σ3,而竖向荷载采用隐式有限元算法的位移增量加载方式,每步加载的位移增量ΔS=0.1 mm,加载总步数依具体方案而定。在本文中,∂V中所模拟的小尺度特征单元总数达到30×30×30=27 000个。对∂V基本参数的拟定,则根据《混凝土重力坝设计规范》(NB/T 35026-2014)[18]的相关规定来进行。由于本文研究的坝基岩体属于岩体完整,结构面不发育的类型,根据坝基岩体特性及相应的岩体工程分类,可以确认Ⅰ类岩体中的坚硬岩,Ⅱ类岩体中的中硬岩,以及Ⅲ类岩体中的软岩属于本文所研究岩体的范围。在这三类岩体中,本文从中选取Ⅲ类岩体中的软岩进行数值模拟研究。对于所研究岩体小尺度特征单元的变形参数(弹性模量和泊松比),先暂不考虑它们的随机性,其取值分别为2×104MPa和0.24;而它们的强度参数(摩擦系数f和黏聚力c)则根据规范中岩体抗剪参数表中所给定f和c的标准值(相当于平均值)参考范围来加以确定。本文按小尺度抗剪强度参数所服从的概率分布类型及变异系数大小不同,拟定了四种计算机数值随机模拟方案(表1)。

表1 f和c参数计算表Tab.1 f and c of the parameters of the table

在对宏观岩体特征单元∂V的小尺度力学参数进行抽样之后,再以位移增量加载的方式进行渐进破坏过程的弹塑性有限元数值模拟。其中增量加载方式为先对∂V施加等量的均布荷载σ2、σ3和等同于σ1(σ1=σ2=σ3)的轴向位移,之后再逐步增加与σ1同方向的轴向位移,直到∂V整体屈服为止。根据一组试验中在若干不同围压(每组试验中的围压均取为1,2,3,4,5 MPa 5个等级)σ2、σ3下∂V整体屈服时所对应的σ1,画出一系列强度莫尔圆,拟合出这些莫尔圆的强度包络线[19],即可得到岩体宏观抗剪强度曲线。
4.3 弹塑性有限元随机模拟的结果
以第一组试验在σ2=σ3=1 MPa的情况下为例,所模拟的∂V逐步屈服过程见图3。

图3 ∂V中小尺度特征单元屈服过程Fig.3 The yield process of small-scale feature element in the ∂V注:图中黑色部分表示已屈服的材料,灰色部分表示未屈服的材料,σ1的单位为MPa,p表示小尺度特征单元的屈服比例。
从以上模拟∂V的逐步屈服过程来看,∂V中的小尺度特征单元的屈服比例是随着竖向荷载σ1的增加而增加的,其过程与文献[12]对一平面大尺度随机场材料所做的破坏演化的过程相似。对于其临界屈服概率pcr的确定,由于不能直接观测到∂V内部的小尺度特征单元的屈服状况,进而不能直接确定其内部非屈服的单元是否相连并形成贯通相对的两个加载面(与σ1相垂直的两个面)的“骨架”,从而只能采取一种间接的方式来确定pcr,即通过∂V逐步屈服过程中所得到的宏观竖向应力----竖向应变曲线(图4),取曲线上面的“转折点”处的宏观应力σ1所对应的屈服比例(σ1等于顶层加载面所有节点竖向应力的平均值),来作为此次模拟的pcr。
从图4的宏观竖向应力----竖向应变曲线可以看出,当σ1-σ3=9.68 MPa时,曲线开始出现明显的弯曲段,此时直线段与弯曲段过渡点的宏观应力所对应的屈服比例为65.73%,与2/3相比相差不大,则通过此次模拟所得到的∂V整体屈服时的竖向宏观强度σ1为10.68 MPa,临界屈服概率pcr为0.657 3。

图4 ∂V整个加载过程的宏观竖向应力----竖向应变曲线Fig.4 Vertical macroscopic stress-strain curve in the process of the loading of the whole ∂V注:图中百分数表示在该宏观应力水平下的小尺度特征单元屈服比例。
当∂V发生整体屈服时,沿σ1方向所截取的若干个横截面中的小尺度特征单元的屈服比例明显大于0.5,非屈服的小尺度特征单元被屈服的小尺度特征单元所包围(图5)。

图5 ∂V整体屈服时若干横截面上小尺度特征单元的屈服状况Fig.5 Yield condition of small-scale feature element of partial cross section when the whole ∂V starts to yield注:图5中h表示沿σ1方向试件的总高度;h′表示沿σ1方向所截取的截面对应的高度。
同样,对第一组试验中的模型在不同水平的围压下(保持σ2=σ3不变)进行相同方式的模拟,最终得到的结果如下(见表2)。

表2 不同水平围压下竖向宏观强度与临界屈服概率模拟结果Tab.2 Results of vertical macroscopic strength and critical yield probability under different levels of confining pressure
由2表可知不同等级围压下所得到的临界屈服概率相差不大,而且都接近2/3,从而验证了前面外推结果pcr3d=2/3的正确性。
根据这一组试验中每个不同等级围压下所得到的竖向宏观强度σ1,可以拟合出相应的莫尔圆的强度包络线(图6)。
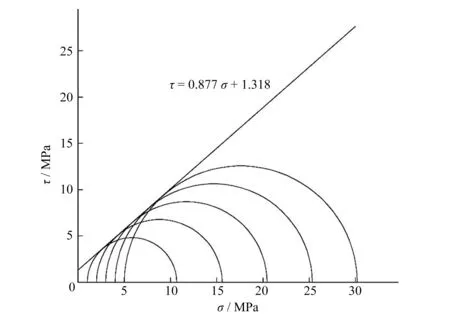
图6 不同围压下的莫尔圆强度包络线Fig.6 Mohr round strength envelope curve under different levels of confining pressure
对其余组进行类似方式的模拟,最终可得到每一组的莫尔圆强度包络线(表3)。

表3 不同组试验下的莫尔圆强度包络线Tab.3 Mohr round strength envelope curve under different groups of experiments

5 岩体宏观抗剪强度的理论推导
∂V中小尺度材料特征单元的屈服是由于作用于相应小尺度特征单元的剪应力过大所致。由于屈服材料要转移超过其自身抗剪强度的多余剪应力给其中尚未屈服而处于弹性状态的材料,从而引起了小尺度材料特征单元的应力重分布。若偏安全地将∂V的小尺度弹性应力场均匀化,并考虑岩体∂V中各点的屈服概率为临界概率pcr时,则可得到岩体宏观抗剪强度的控制方程为[11]:
(8)
式中:fτ(τ)为小尺度岩体抗剪强度τf(r)=f(r)σn+c(r)的一维概率密度,其中f(r)和c(r)分别为∂V的小尺度摩擦系数、黏聚力随机场;σn、τn和τf(r)分别为∂V中的小尺度弹性应力场均匀化后的小尺度弹性正、剪应力和小尺度抗剪强度,且σn和τn还分别表示∂V中的宏观正、剪应力;Tn为∂V整体屈服时的小尺度特征单元的最大抗剪强度;pcr为∂V整体屈服时的临界屈服概率;τcr为岩体的宏观抗剪强度。
若假定小尺度岩体的抗剪强度参数f(r)和c(r)都服从正态分布,则τf(r)同样也服从正态分布,并且:
(9)
(10)
(11)

由前面有限元随机模拟结果可知∂V发生整体屈服时的临界屈服概率pcr=2/3,则此时可直接令公式(8)中第二个式子中的pcr为2/3,然后将fτ(τ)转换成标准正态分布,由标准正态分布表可求得Tn的值,再把Tn代入公式(8)的第一个式子中,即可求得岩体的宏观抗剪强度τcr,其中τcr的具体计算公式为:
(12)
若小尺度摩擦系数f和黏聚力c不相关,亦即ρfc等于0,相应τcr的计算公式为:
(13)
与文献[11]所推导的岩体宏观抗剪强度的上、下限公式τcrs和τcrd作比较,在同一宏观正应力σn的水平下,则有
τcrs>τcr>τcnd
(14)
其中τcrs和τcrd分别为:
(15)
(16)
岩体宏观抗剪强度的上、下限理论公式在数值上分别与小尺度岩体抗剪强度的算术平均值和小值平均值相等,还与分别按保证率50%和78.7%所取的小尺度岩体抗剪强度相等。由于岩体宏观抗剪强度介于相应的小尺度岩体抗剪强度的算术平均值和小值平均值之间,因此其保证率也应介于50%和78.7%之间。通过分析,岩体宏观抗剪强度理论公式在数值上与按保证率70.7%所取的小尺度岩体抗剪强度相等(图7)。
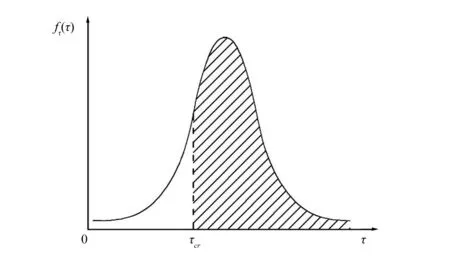
图7 小尺度岩体抗剪强度概率密度函数Fig.7 Probability density function of small-scale rock mass shear strength
由于当小尺度岩体的抗剪强度参数f(r)和c(r)都采用服从正态分布计算时,会出现一些参数的抽样值为负的情况,与工程实际不符。若将f(r)和c(r)都采用服从对数正态分布计算,则能很好地避免这一情况的出现,同时也符合工程抗剪试验成果的统计规律。此时,可得出τf(r)同样也服从对数正态分布,即:
(17)
其中λ和ζ分别为:
(18)
(19)
类似的,若令pcr等于2/3,则可推导出f(r)和c(r)在服从对数正态分布条件下的岩体宏观抗剪强度的计算公式τcr,即有:
(20)
其中φ(x)为标准正态分布函数,即:
(21)
6 岩体宏观抗剪强度理论公式试验验证
6.1 理论公式与数值模拟试验结果的对比
图8给出了岩体宏观抗剪强度的有限元随机模拟值(表3)和分别按公式(13)和(20)计算的理论值的对比情况。从中可以看出,在同一宏观正应力σ水平下,理论曲线和莫尔圆强度包络线分别所对应的宏观剪应力(即宏观抗剪强度)差异不大。

图8 不同分布类型情况下的宏观抗剪强度理论值与数值模拟值的对比图Fig.8 Comparison of theoretical value and numerical simulation of macroscopic shear strength in the case of different distribution注:图中的CV表示黏聚力c的变异系数CVc,根据CVc的值及其分布类型可以确定对应组的试验曲线。
6.2 几组数值模拟试验结果之间的相互比较
图9给出了岩体宏观抗剪强度的有限元随机模拟值(表3)之间的对比情况。从中可以看出,材料的力学参数服从何种分布类型,对最终所得到的宏观抗剪强度曲线没有太大的影响,反而是材料的非均质程度[20](其力学参数用变异系数的大小来反映)对其有较大的影响。当材料的摩擦系数f和黏聚力c的变异系数较大时,即使两者的均值分别同前面的对应参数保持一致,且不论材料参数所服从的分布类型,最终得到的宏观抗剪强度曲线均有一定的下降,且下降的幅度最大约为7%。

图9 四组有限元数值模拟值之间的对比图Fig.9 Comparison of four sets of finite element numerical simulation
6.3 弹性模量和泊松比随机性对宏观抗剪强度的影响
表4 E和μ参数计算表Tab.4 E and μ of the parameters of the table
图10给出了是否考虑了弹性模量和泊松比的随机性的岩体宏观抗剪强度的有限元随机模拟值之间的对比情况。从中可以看出,无论材料参数是服从正态分布还是对数正态分布,是否考虑E和μ的随机性对最终计算所得的宏观抗剪强度曲线影响均不大。

图10 不同分布情况下是否考虑E和μ随机性的宏观抗剪强度曲线的比较Fig.10 The comparison of the macroscopic shear strength curves whether the randomness of E and μ is considered in the case of different distribution
7 结 论
(1)本文通过结合随机场和逾渗临界理论这两种方法,分析了同一地质单元内的大尺度基岩整体屈服时的临界特性,推导了用小尺度岩体试块抗剪试验结果确定岩体宏观抗剪强度的理论计算公式,并通过弹塑性有限元随机模拟验证了所推导的理论公式的正确性。研究结果表明:宏观岩体特征单元∂V整体屈服时的临界屈服概率pcr约为2/3,且所推导的宏观抗剪强度的理论值与通过数值模拟分析计算所得到的结果相差不大。
(2)通过对比计算分析可知,在摩擦系数f和黏聚力c实际可能变异的范围内,不管其分布类型是正态分布还是对数正态分布,对所得到的宏观抗剪强度曲线的影响不大。而两者的变异系数的大小,对宏观抗剪强度曲线却有一定的影响,即当f和c的变异系数较大时,其相对应的宏观抗剪强度曲线有一定的下降。此外,弹性模量E和泊松比μ的随机性对其宏观抗剪强度的影响很小。
