基于MOSCEM-UA的水文模型多目标参数优化研究

2019-01-21杜彦臻刘红利赵天宇林洪孝

中国农村水利水电 2019年1期

杜彦臻，刘红利，赵天宇，林洪孝，王刚

(1.山东农业大学水利土木工程学院，山东泰安 271018； 2.南水北调东线山东干线有限责任公司，山东济南 250000)

0 引言

国内外对流域水文模型的研究不断深入，通过对水文现象的合理概化，流域水文过程及各水文要素计算构建流域水文模型。随着计算机技术的发展，水文模型在水文预报、水库防洪以及水资源管理等方面应用广泛。世界气象组织以模型的精度为标准进行模型对比，发现水文模型在湿润地区模拟精度较好。其中国内应用较多的新安江模型，也主要适应于以蓄满产流为主的湿润地区，在典型的半湿润、半干旱地区常会有蓄满和超渗产流两种产流机制并存的流域。因此，研制适用于半湿润、半干旱地区的混合产流模型十分必要。水文模型预报精度与模型的参数优化率定选择密切相关，模型参数是用来评估实测与模拟数据的接近程度。国内外水文学者对自动校准方法进行大量研究，自动优化法利用计算机的速度和能力，客观且相对容易操作，从而优选出理想参数。

模型参数的优化方法主要有单目标和多目标优化法，目前国内应用较多的是遗传算法、罗森布洛克法及SCE-UA等单目标算法[1]，对多目标优化算法应用相对较少。单目标算法虽简单快捷，但由于水文模型结构不足，单目标只能捕捉单一方面的水文特征，不能较全面的对水文特征进行综合考虑，从而没有得到水文学家的广泛认可，要使模拟结果的准确性进一步提高，需进行多目标优化。水文模型参数校准实践经验表明，预报过程中多个目标之间相互制约，任何单目标函数都不足以准确的评价观测数据的所有特征。因此为提高模型预报精度采用多目标优化方法势在必行，国外应用较多的多目标方法如：多目标粒子群算法[2]、MOSCDE算法[3]、NSGA-Ⅱ[4]、MOCOM[5]以及MOSCEM-UA算法等。

以沁水河流域为例，采用MOSCEM-UA算法基于垂向混合产流模型的基础上，对流域的降雨、径流、蒸发、洪水资料进行次洪模型多目标参数优化。

1 研究区垂向混合产流模型

蓄满和超渗是两种典型的产流模型。湿润地区降雨产流以蓄满产流为主，干旱地区以超渗产流为主，即使在典型的湿润或干旱地区也常会出现两种产流机制并存的情况。包为民[6]教授首次提出垂向混合产流模型[7]，该模型在纵向上将蓄满—超渗产流进行混合。沁水河流域位于北方的半湿润地区，单一的产流模型不能准确的模拟研究区产流量，因此提出适合该流域的混合产流计算方法十分重要。

模型结构主要分为4部分[8]：①产流部分用蓄满—超渗垂向混合产流概念；②蒸散发部分按上、下、深三层蒸发模式；③水源部分用EX次抛物线形自由水蓄水曲线划分地表、壤中和地下径流3种水源；④汇流部分地面汇流用单位线法、地下汇流用线性水库法。此外，模型依据沁水河流域特殊的水文特征，考虑人类活动对水文循环要素的影响，即加入河道内农业灌溉、生活取水和水利工程等影响因素，构成了完整的适应该流域的垂向混合产流模型。

混合产流下渗计算，雨量P到达地面，通过空间分布下渗曲线，划分地面径流RS和下渗水量FA，FA向下运动，土壤缺水量大时补充含水量，不产流；土壤缺水量小时补足土壤缺水后，产生地面以下径流RR。依此划分为地面径流和地面以下径流(壤中流和地下径流)。地面径流RS根据改进后的格林—安普特下渗公式[9]计算，计算公式为：

(1)

RS=P-FA

(3)

式中：FM为流域平均下渗能力，mm；fc为稳定下渗率，mm；KF为渗透系数；WM为流域平均蓄水容量；W为流域实际土壤含水量，mm；BF为反映下渗能力空间分布特征的参数；P为扣除雨间蒸发的降雨量，mm。

地下径流RR采用蓄满产流结构计算，计算公式为：

(4)

式中：Wmm为蓄水量最大值。

因此，产流总量为R=RS+RR。

2 MOSCEM-UA算法

2.1 MOSCEM-UA算法简介

多目标混合复杂演化MOSCEM-UA(Multi-objective Shuffled Complex Evolution Metropolis)算法[10]是Vrugt等[11]在2003年提出了一种新的多目标算法，由阿姆斯特丹大学和亚利桑那大学合作开发，是在Duan等提出的SCE-UA算法[12]的扩展，它结合了SCE-UA与马尔可夫链Metropolis强度的一种新的适应性分配方法。MOSCEM-UA可被视为建立的水文模型校准基准，并成功地进行模型参数校准，被证明为一种稳健和有效的全局优化方法。

MOSCEM-UA是对混合复杂演化都市(SCEM-UA)全局优化算法的一种改进，它使用Pareto主导的概念，而不是直接进行单目标函数评估，将最初的点群发展为一组解决方案稳定分布Pareto解集，该算法迭代效率高，逼近速度快。其算法的流程见图1、图2。

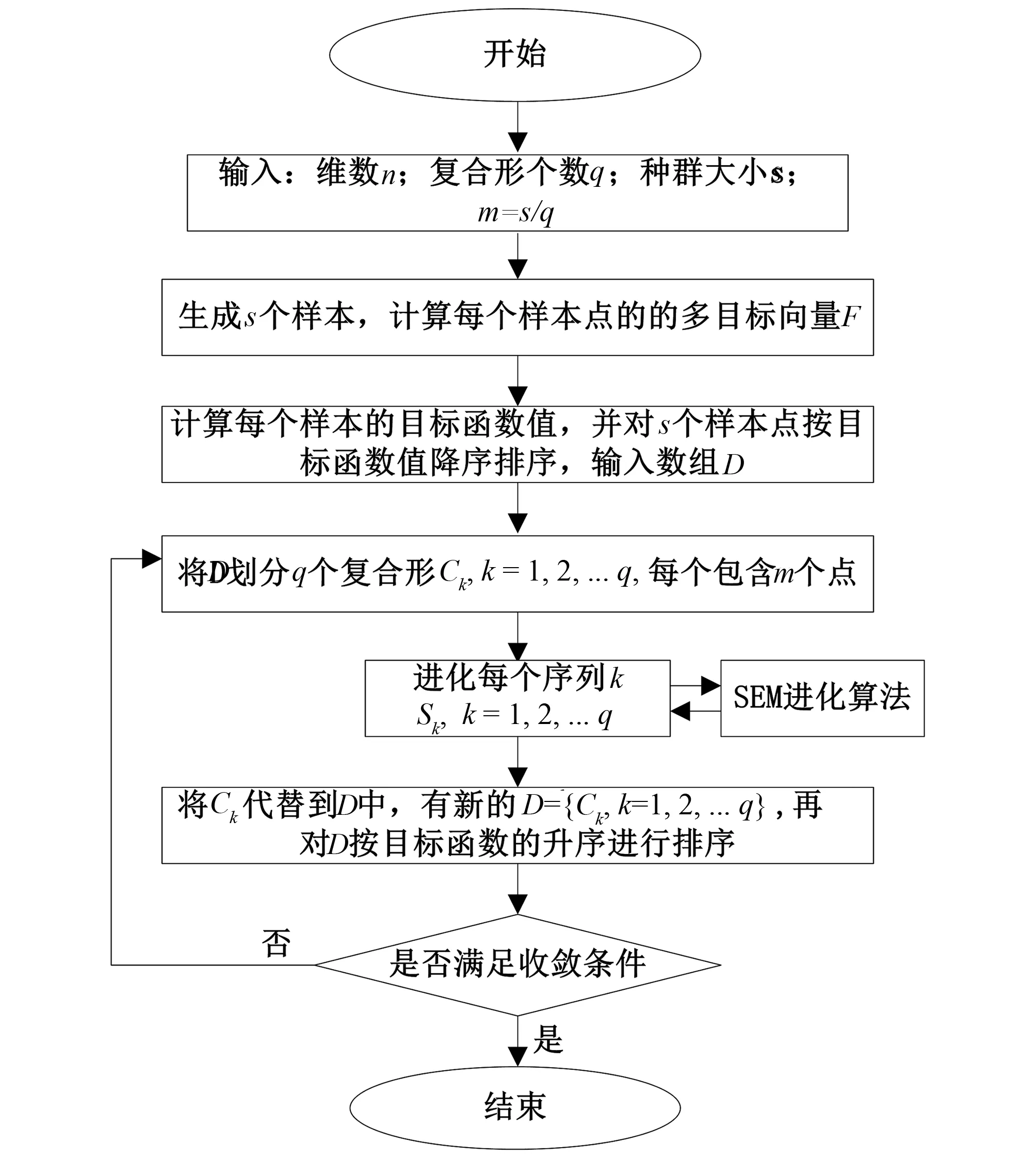
图1 SCE-UA算法流程图Fig.1 Flowchart of the SCE-UA algorithm

图2 MOSCEM-UA大都会演化算法流程图Fig.2 Flowchart of the Sequence Evolution employed in the MOSCEM‐UA algorithm.

2.2 算法参数设置

SCE-UA算法是在单纯形法基础上根据生物竞争进化和基因算法的原理综合而成，可一致、快速、合理地搜索到水文模型参数的全局最优。虽然算法参数较多，但绝大部分都可取经验值，只有复合形个数p根据具体问题确定。p主要决定收敛精度及快慢，在取值范围内p值越大越适应于高阶非线性问题，根据沁水河流域水文要素特征本文选取p=8时对参数全局最优及参数间的关联性都相对较好，且能够对参数结果进行较合理的分析优选。

SCE-UA算法参数设置具体为：m=2n+1，q=n+1，s=pm，α=1，β=2n+1。MOSCEM-UA算法有四个参数由必须具体问题确定：种群大小s，复合形个数p，进而确定每个复合形样本点数m=s/p，每个复合形进化步数L，后代接受概率比例因子β，本算法使用L=m/4和β=1/2。因此，MOSCEM算法需要指定变量是s和p。本文所选的垂向混合产流模型中参数个数n=15，复合形个数p=8，种群大小s=8×31=248，最大迭代次数I=1 000，算法终止条件为达到设定最大迭代次数或经过多次循环后参数值和目标函数均无明显提高。

3 模型参数的多目标优化

3.1 Pareto非劣解原理简介

对于单目标问题，确定目标函数的最优非劣解时常采用权重法对各目标函数赋予权重系数来确定。但在多目标参数优化时，权重法会导致“均化效应”，难以准确评价观测数据的多样性特征。因此，基于多目标函数参数优化不再是单一的“最佳”参数集，而是包括在可行参数空间中对多目标之间折中解决方案的Pareto集。

Pareto非劣解集定义了参数中的最小不确定性，在不牺牲另一个参数的情况下主观相对优选使F(θ)的特定分量最小化，其目的是同时最小化两个参数的目标函数F(θ1)、F(θ2)。Pareto解决方案集见图3，点A和点B表示每个单独的目标函数F(θ1)、F(θ2)最小化的解决方案，连接A和B的线段为Pareto解集，在多目标意义上γ是解集Δδ中一个比任何点都具优越性的元素。数学上定义Pareto最优集为不劣于参数空间中任一参数的解的集合，即参数θ1劣于参数θ2，当且仅当满足不存在i使

Fi(θ1)Fi(θ2)i=1,…,m

(5)

图3 Pareto非劣解集图Fig.3 Pareto noninferior solutions set

3.2 优选参数设置

垂向混合产流模型进行次洪模型模拟时以Δt为时段长，模型共有15个参数见表1，其中不敏感参数直接取其中间值，其中模型模拟较为敏感5个参数为BF、KF、fc、CS、L。

表1 模型参数上下限Tab.1 Model parameters upper and lower limits

3.3 目标函数及精度评价指标

不同的目标函数用来评价水文过程的不同特征，多目标优选时，多个目标之间往往存在冲突，当某一目标函数较优时必定会牺牲其他目标函数，故目标函数的选择对水文模型的预报精度有较大的影响，本文采用3个目标函数作为垂向混合产流模型次洪模拟标准，公式如下。

(1)均方误差RMSE：表示实测与模拟值的吻合程度。

(6)

(2)洪量目标控制：表示整体洪量拟合以保证水量平衡。

(7)

(3)洪峰目标控制：表示洪峰相对误差侧重于洪峰流量拟合。

(8)

水文模型精度误差评定指标主要以场次洪量相对误差(RE)、洪峰相对误差(REPF)以及Nash-Sutcliffe效率系数(NSE)为标准，具体公式为：

(9)

REPF=|Qo,i-Qs,i|/Qo,i×100%

(10)

(11)

式中：Qo,i为实测流量，m3/s；Qs,i为模拟流量，m3/s；m为资料序列长度；N为场次洪水数。

4 实例应用

4.1 研究区概况

沁水河流域属胶东半岛低山丘陵区，地势为南高北低，流域属暖温带半湿润大陆性季风气候，多年平均降水量为651.9 mm，年平均气温12.7 ℃，四季变化分明。沁水河为典型的山溪性雨源型河道，河道流量与降水量变化规律相一致，且年内、年际变化大，枯季流量较小，洪水主要集中在汛期。沁水河上游河床受水流冲刷较大，中游侧蚀严重，下游沉积，形成流水不畅现象。中下游建立拦河闸坝后，中低水时，拦蓄上游来水，汛期，受上游闸坝拦蓄影响，洪水过程发生形变，洪峰比天然河道滞后，洪峰洪量也往往比天然河道偏大。该流域测验断面上游共计有9座小型水库，测验断面及以上有4座拦河闸坝，测验断面以下有2座拦河闸坝，7座塘坝。流域水文站监测断面以上控制流域面积为168 km2，共有5个雨量(分别是牟平、十六里头、玉林店、徐家疃、西柳庄)、1个流量站(牟平水文站)和1个蒸发站(门口水库)。本研究应用该流域1981-2000年20 a的实测日降雨、蒸发、流量资料用于垂向混合产流模型参数优化率定，其中1981-1992年为率定期，1993-2000年为验证期。

4.2 结果分析

MOSCEM-UA算法优化得到Pareto集合的参数分布见图4所示，对15个参数值均基于上下限(0， 1)之间进行归一化处理，连接参数的每条线表示一个Pareto集。本例选取5个敏感参数BF、KF、fc、CS、L作为优选对象对其取值范围的边界进行归一化处理。由图看出，Pareto集中最优参数的变化幅度较大，取值范围较小的参数容易确定，取值范围较大的参数不易确定。因此，算法得到Pareto解能够捕获大多数参数的不确定性信息，且参数最优分布基本在取值范围之内没有越界趋势。

图4 Pareto解对应参数归一化空间Fig.4 Pareto solution corresponding parameter normalized space

采用MOSCEM-UA算法产生Pareto集合对多目标(RMSE目标F1、洪量目标F2、洪峰目标F3)进行计算得到50个Pareto散点解，三维目标参数优化Pareto散点解见图5所示。二维Pareto解见图6所示，左边的黑点表示目标函数空间上的Pareto前沿，Pareto前沿点是最好的单一目标函数解决方案。可以看出，Pareto前沿解目标函数间存在明显的制约关系，两者不能同时最优，必须牺牲一方来取得彼此的最优值，因此MOSCEM-UA算法对多目标优化计算可以得到一组多个目标都较优的Pareto非劣解集。

图5 三目标参数优化Pareto解散点图Fig.5 The three-dimensional plots of the Pareto solutions

图6 Pareto解二维散点图Fig.6 Pareto solution to two-dimensional scatter plot

预报方案的效果评定和有效性检验，一般将良好代表性的系列资料分为率定期和验证期，通过模拟与实测水文要素间的比较来检验预报方案的效果与有效性。《水文情报预报规范》(SL250-2000)规定：评价和检验方法采用统一的许可误差和有效性标准对预报方案进行评定和校验。依据规范在预报过程当中，洪量、洪峰相对误差取预测期内实测值的20%作为允许误差。由表2看出，洪量指标RE在四个目标函数方案中的率定期合格率达到75%，验证期达到100%，其中三目标同时考虑时误差最小，其次是洪量目标F2；洪峰指标REPF在F3中最小；NSE值的精度等级大多数在乙级及以上，且三目标优于单目标F1、F2及F3，预报结果较好。由表可以看出，在考虑单目标最优情况下，最终的优选结果偏向于该目标函数所体现的水文特征，其他目标函数未必能达到令人满意的结果。因此单一目标优化不能准确全面的校准水文模型及水文过程的性能特征，需要通过多目标优化来完成。

表2 垂向混合产流模型预报精度评价结果Tab2 Vertical mixed flow model forecast accuracy evaluation results

图7，8 分别是选取率定期和验证期以协调解参数模拟过程的效果图，基于洪量目标、均方根目标、洪峰目标及三目标的四种组合下进行洪水模拟， 19810701场次洪水可以看出，三目标优化率定统筹了洪量过程及洪峰峰值等特性，整体结果较优。模型参数多目标优化结果通过最终优化得到的pareto参数协调解见表3，由此参数进行检验期19970820场洪水模拟，且效果较好。结果表明，多目标优化在整体流量过程线上吻合趋势较好，且率定期的效果优于验证期的效果，进一步验证了多目标参数率定的有效性和优越性。