基于不同ELM的西北旱区参考作物蒸散量模拟模型

徐 颖，张皓杰，崔宁博,2，冯 禹，胡笑涛，龚道枝

(1.四川大学 水力学与山区河流开发保护国家重点实验室、水利水电学院，四川 成都 610065；2.南方丘区节水农业研究四川省重点实验室，四川 成都 610066；3.西北农林科技大学 旱区农业水土工程教育部重点实验室，陕西 杨凌 712100；4.中国农业科学院 农业环境与可持续发展研究所作物、高效用水与抗灾减损国家工程实验室，北京 100081)

0 引 言

参考作物蒸散量(reference crop evapotranspiration，ET0)是计算作物需水量的关键因子，对灌溉系统设计和农业水资源管理具有重要意义[1]，其精准预报对作物需水量估算、水资源优化调配及实现智慧灌溉等有重要价值。目前ET0计算模型有60多种，主要可归为辐射法、温度法、综合法和水面蒸发法等[2]。1998年联合国粮食与农业组织(Food and Agriculture Organization of the United Nation，FAO)将Penman-Monteith(P-M)模型作为ET0计算的标准模型[3]，P-M模型虽然是FAO推荐的最佳估算模型，但需要较完整的气象资料，而很多地区由于标准气象站点少且分布不均、设备不足等问题，常发生气象资料缺失的情况，因此许多适用于较少气象因子输入的ET0计算模型被提出，如温度法中的Hargreaves-Samani(HS)[4]、Blaney-Criddle[5]等模型，辐射法中的Priestley-Taylor(P-T)[6]、Makkink[7]等模型，经验公式法中的Irmark-Allen[8]等模型。

随着机器学习(machine learning，MC)的发展，越来越多机器模型被应用于ET0模拟，如Kumar[9]、Gorka[10]等对BP神经网络(Back-Propagation，BP)模型在ET0模拟中的应用进行探讨，证实BP神经网络在各自研究区域内模拟结果良好，但BP神经网络模型学习速率固定，收敛速度慢且存在局部极值的问题。Tabari[11]等采用支持向量机(support vector machine，SVM)和自适应模糊推理系统(adaptive neural fuzzy inference system，ANFIS)算法对ET0进行模拟，发现该模型精度高于Blaney-Criddle、Hargreaves、Priestley-Taylor等模型。崔远来[12]等利用遗传算法(genetic algorithm，GA)优化神经网络(Artificial neural network，ANN)模型，克服了BP网络输入层、隐含层节点确定的盲目性，提高了进化神经网络(GA-ANN)的精度和适应性。张育斌[13]等基于典型的H-S模型、Mc Cloud模型和简易神经网络算法提出五变量输入、LM算法的三层网络结构改进模型，发现改进模型在气象资料欠缺、气温异常波动情况下的ET0模拟精度有明显提升。

极限学习机自被提出已被广泛用于多个领域。Abdullah[14]、冯禹[15,16]等分别在伊拉克地区和川中丘陵区采用极限学习机对ET0进行模拟，取得了良好的模拟效果，发现ELM模型运行速度快、精度高、泛化能力好。极限学习机在训练过程中只需调整隐含层节点数，便可获得唯一最优解，合理确定隐含层节点数对模型精度有重要意义。邹伟东[17]等利用经验模态分解(empirical mode decomposition，EMD)方法确定隐含层节点数，建立了日光温室温度湿度模拟模型，以改善因试凑法确定隐含层节点数引起的缺陷。但目前尚无人研究隐含层节点数对ELM模型模拟ET0精度影响。并且国内外学者在运用ELM模型模拟ET0时，均默认激活函数为“sig”，事实上还存在“sin”、“hardlim”、“radbas”等激活函数，关于不同激活函数对于ELM模拟ET0精度的影响的研究尚待开展。

本文构建基于不同激活函数“sin”、“radbas”、“hardlim”的ELM模型来模拟ET0，分析其模拟结果提出适用于ELM模型的激活函数，在精度较高的ELM模型中探究最优隐含层节点数，并同物理模型进行对比，验证ELM模型精度，寻求适用于中国西北地区的ET0模拟模型，以期为中国西北旱区农业水资源高效利用提供参考。

1 材料与方法

1.1 研究区概况

中国西北旱区位于31°35′～49°15′N，73°25′～110°55′E，包括陕西、新疆、甘肃、青海、宁夏、内蒙古西部等地，具有干旱缺水、荒漠广布等特点。从旱区划分标准来看，西北地区大部分地区降水在400 mm以下，多数地区在50～200 mm之间，属于干旱、半干旱区，而其蒸发量高达2 000～3 000 mm，更加剧了西北地区的干旱缺水。西北地区水资源总量为3 017.5 亿m3，其中农业用水量为2 492.5 亿m3，占西北旱区水资源总量的82.6%，比全国农业用水在水资源总量中占比高21.3%[18]。

本文选取西北地区若羌、绥德、乌鲁木齐、西宁4个气象站点(站点分布见图1)1993-2016年逐日气象数据，包括日最高气温Tmax、日最低气温Tmin、日照时数n、距地面10 m高处的风速(计算时采用FAO风廓线关系[3]换算为2 m高度风速u2)和2 m高度相对湿度(relative humidity，RH)。气象资料来源于国家气象信息中心，经过严格筛选核对，质量良好。研究取1993-2012年数据为训练集，取2013-2016年数据为模拟集。

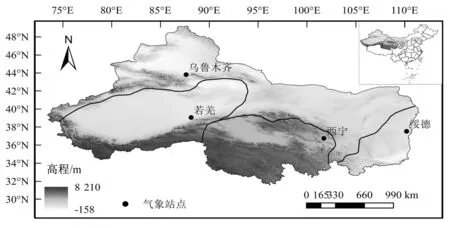
图1 站点分布图Fig.1 Distribution of meteorological station

1.2 研究方法

本文以1998年联合国粮食与农业组织(Food and Agriculture Organization of the United Nation，FAO)推荐的FAO-56 Penman-Monteith(P-M)模型计算结果作为ET0标准值，选取温度法中的Hargreaves-Samani(H-S)、辐射法中的Makkink(MK)、Irmark-Allen(I-A)等3种在西北地区ET0计算精度较高的物理模型与P-M模型进行比较，各模型及计算公式如表1所示。

表1 参考作物蒸散量计算模型Tab.1 Calculation models of reference crop evapotranspiration

注：ET0为参考作物蒸散量，mm/d；Rn为净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；Tmean为平均气温，℃；es为饱和水汽压，kPa；ea为实际水汽压，kPa；Δ为饱和水汽压-温度曲线斜率，kPa/℃；γ为湿度计常数，kPa/℃；C0为转换系数，取0.000 939；Ra为大气顶层辐射，MJ/(m2·d)；Rs为太阳辐射量，MJ/(m2·d)；α为经验系数，取为1.26；n为日照时数，h/d；RH为相对湿度，%。

1.3 模型构建

1.3.1 极限学习机原理

极限学习机(extreme learning machine，ELM)是一种基于单隐含层前馈神经网络(Single-hidden Layer Feedforward Neural Network，SLFN)的新算法，该算法由输入层、隐含层和输出层组成，ELM拓扑结构绘于图2。

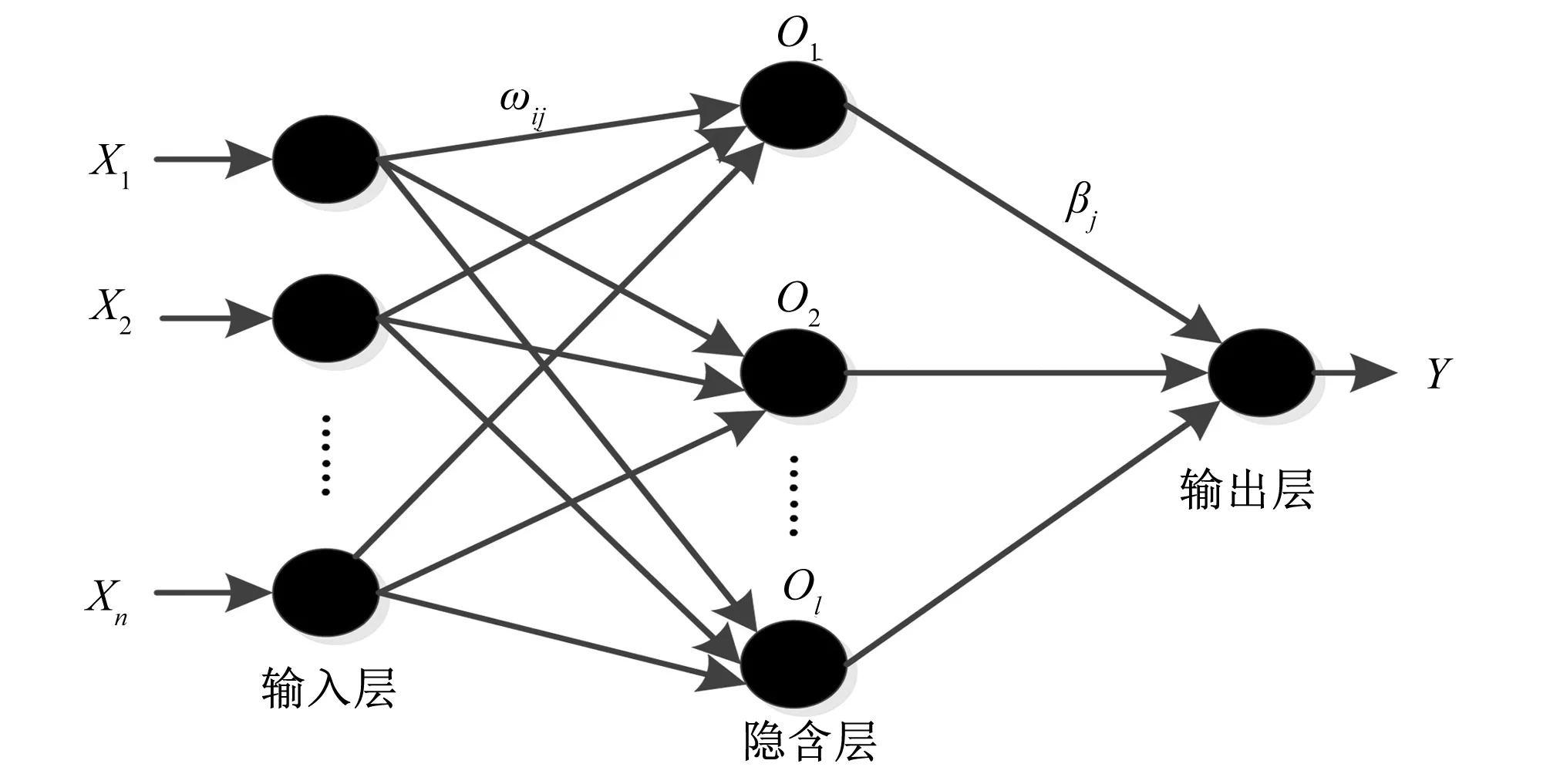
图2 极限学习机(ELM)拓扑结构图Fig.2 Topological structure of extreme learning machine

对于任意N个样本(Xi，ti)，假设输入层神经元个数为n，对应n个输入变量(X1～Xn)；隐含层有l个神经元(O1～Ol)；输出层神经元个数为m，对应m个输出变量(Y1～Ym)；设输入层与隐含层的连接权值ωl×n，隐含层与输出层的连接权值βl×m；设隐含层神经元的激活函数为g(ω，X，b) ，则ELM网络的输出表达式为：

(5)

式中：βj=(βj1，βj2，…，βjm)T为第j个隐含层神经元与输出变量的连接值向量；ωij=(ωj1，ωj2，…，ωjn)T为第i个输入变量与第j个隐含层神经元的连接值向量；bj为第j个隐含层神经元的阈值。

由式(5)可得：

H·β=t

(6)

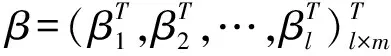
算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值且在训练过程中保持不变，故只需设置隐含层神经元个数l即可计算出隐含层与输出层的连接权值，获得唯一最优解。因此隐含层与输出层的连接权值β可以由式(6)的最小二乘解得：

(7)

式中：H+为H的MP广义逆矩阵。

最小二乘解β求得后，训练过程即完成。

根据ELM学习算法的步骤，可知其激活函数g(ω，X，b)与隐含层神经元个数l对ELM模型的训练和模拟有着显著影响，故选择合理的激活函数与合适的隐含层神经元个数是至关重要的。

1.3.2 模型构建

仅设置ELM模型的隐含层节点数l与激活函数g(ω，X，b)，根据初步模拟结果，设置隐含层节点数l为100，选取如下3个激活函数[19]：Sine函数、径向基传输函数(radbas)、Hardlim函数。构建气象因子输入相同情况下不同激活函数的ELM模型。模型完整训练过程及具体的程序见文献[20]。

Sine函数：

g(ωijX+bj)=sin(ωijX+bj)

(8)

径向基传输函数(radbas)：

(9)

Hardlim函数：

(10)

1.4 模型验证因子

选用6个评价因子[21]反映不同模型模拟精度，具体公式如下。

均方根误差RMSE

(11)

决定系数R2：

(12)

纳什系数NSE：

(13)

平均相对误差MRE：

(14)

平均绝对误差MAE：

(15)

整体评价指标[22]GPI：

(16)

2 结果分析

2.1 基于不同激活函数ELM模型的参考作物蒸散量日值模拟

分析基于“sin”、“radbas”、“hardlim”等3种激活函数的ELM模型在不同气象因子组合输入下的精度。ELM-sin、ELM-rad、ELM-hard的模拟结果分别如表2、表3和表4所示。

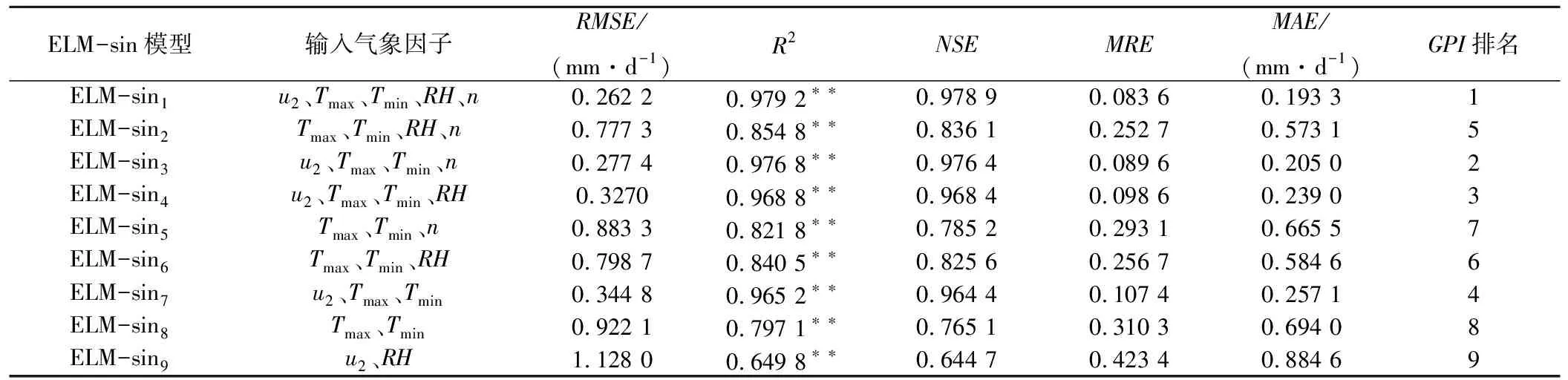
表2 不同气象因子输入下ELM-sin参考作物蒸散量日值模拟精度Tab.2 Reference crop evapotranspiration simulation accuracy of ELM-sin with different meteorological factors

注：** 表示1%水平上的极显著相关，ELM-sin、ELM-rad、ELM-hard分别代表激活函数为sin、radbas、hardlim的ELM模拟模型，下同。

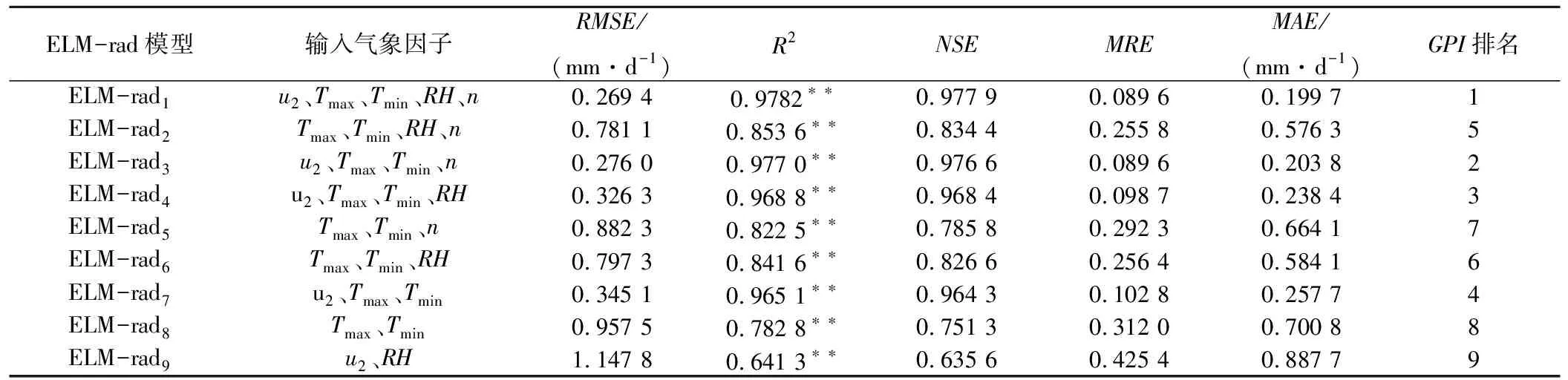
表3 不同气象因子输入下ELM-rad参考作物蒸散量日值模拟精度Tab.3 Reference crop evapotranspiration simulation accuracy of ELM-rad with different meteorological factors

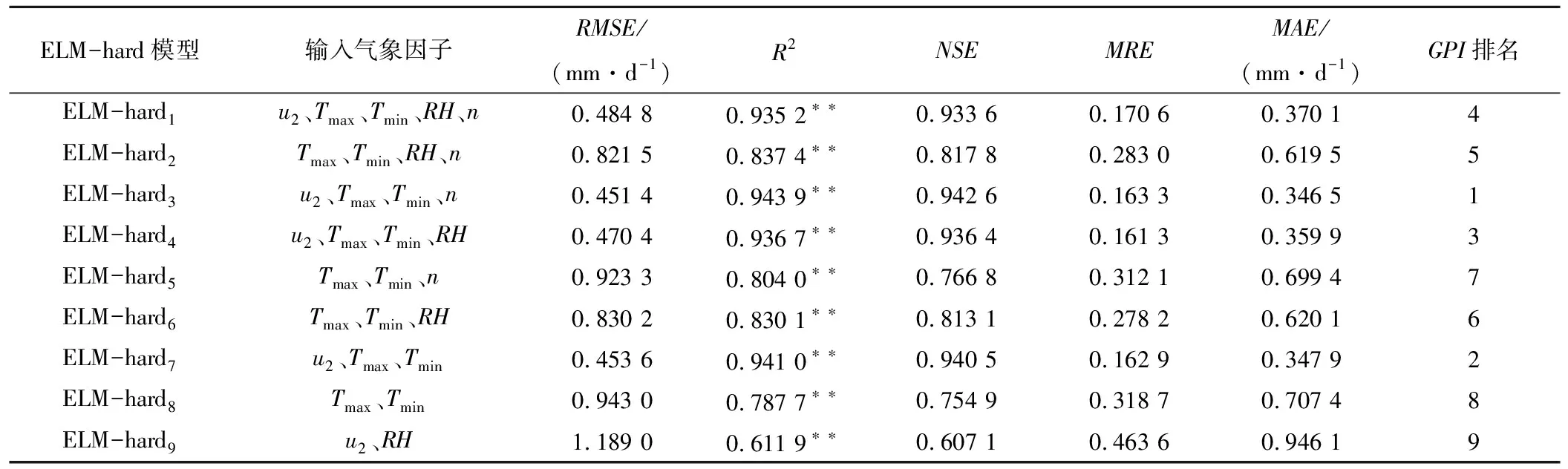
表4 不同气象因子输入下ELM-hard参考作物蒸散量日值模拟精度Tab.4 Reference crop evapotranspiration simulation accuracy of ELM-hard with different meteorological factors

输入5个气象因子时，ELM-sin1模型与ELM-rad1模型的R2、NSE和RMSE分别为0.979 2和0.978 2、0.978 9和0.977 9、0.262 2 mm/d和0.269 4 mm/d，而ELM-hard1的R2、NSE和RMSE分别为0.935 2、0.933 6和0.484 8 mm/d。因此，ELM-hard1精度较低，其中ELM-sin1的可靠性最高。

输入4个气象因子时，ELM-sini、ELM-radj和ELM-hardk(i，j，k=2，3，4)，GPI均排名前5，模型准确性较高。ELM-sini和ELM-radj(i，j=3，4)的R2和NSE均大于0.96，ELM-hardk(k=3，4)的R2和NSE均小于0.95，因此ELM-sin和ELM-rad模型较ELM-hard模型更好地反映了相同气象因子组合与ET0的映射关系。并且，ELM-sin3和ELM-rad3的MRE均为8.96%，MAE分别为0.205 0 mm/d和0.203 8 mm/d，可见ELM-rad3较ELM-sin3模拟偏差更小；而ELM-sin4和ELM-rad4的R2和NSE相等，RMSE分别为0.327 0 mm/d和0.326 3 mm/d，ELM-sin4的RMSE更大，表明ELM-rad4准确性更高。同时，缺失u2的ELM-sin2、ELM-rad2和ELM-hard2模型较缺失RH、缺失n的ELM-sini、ELM-radj和ELM-hardk(i，j，k=3，4)模型精度更低，说明风速对西北旱区ET0的影响较大，这与汪彪[22]、刘宪峰[23]等得出的风速是影响西北地区的ET0计算主要因子之一的结论一致。

输入3个气象因子时，以u2、Tmax、Tmin作为输入项的ELM-sin7、ELM-rad7和ELM-hard7的GPI均排名前4，三者的R2均大于0.90，其中ELM-hard7的R2和RMSE分别为0.941 0和0.453 6 mm/d，ELM-sin7和ELM-rad7的R2均大于0.96，RMSE分别为0.344 8和0.345 1 mm/d，说明ELM-sin7和ELM-rad7精度高于ELM-hard7，且ELM-sin7的模拟偏差更小。分析ELM-sini与ELM-radj(i，j=5，6，7)的模拟结果，u2对ET0模拟精度的影响最大，RH次之，n影响最小。Saeid[24]等在伊朗的研究表明，伊朗部分地区ET0对RH较为敏感，张青雯[25]等发现n是影响西南五省ET0的主导因素，而本研究中u2对ET0模拟精度的影响更为显著，可见各气象因子对不同地区ET0的影响和贡献率有较大差异。

输入2个气象因子时，ELM-sini、ELM-radj和ELM-hardk(i，j，k=8，9)模型精度明显下降。仅输入温度时，ELM-sin8的R2为0.797 1，而ELM-rad8和ELM-hard8的R2分别为0.782 8和0.787 7，说明仅输入温度时，ELM-sin8的精度最高，ELM-rad8次之，ELM-hard8精度最低。此外，结果表明基于温度的ELM-sin8、ELM-rad8和ELM-hard8的精度较基于RH与u2的ELM-sin9、ELM-rad9和ELM-hard9精度更高，这与曹雯等[26]对西北旱区ET0敏感性分析得出的ET0对温度辐射的敏感系数高于对相对湿度的敏感系数结论一致。

2.2 隐含层节点数对ELM模型精度的影响

仅输入Tmax、Tmin、u2时，基于激活函数“sin”的ELM-sin7模型ET0模拟精度较高，可见该模型在气象资料缺失时在西北地区适用性强，因此本文分析隐含层节点数目对ELM-sin7模型ET0模拟精度的影响。基于ELM-sin7模型，设置不同的隐含层节点数，得出隐含层节点数与各模型精度评价指标的关系绘于图3。

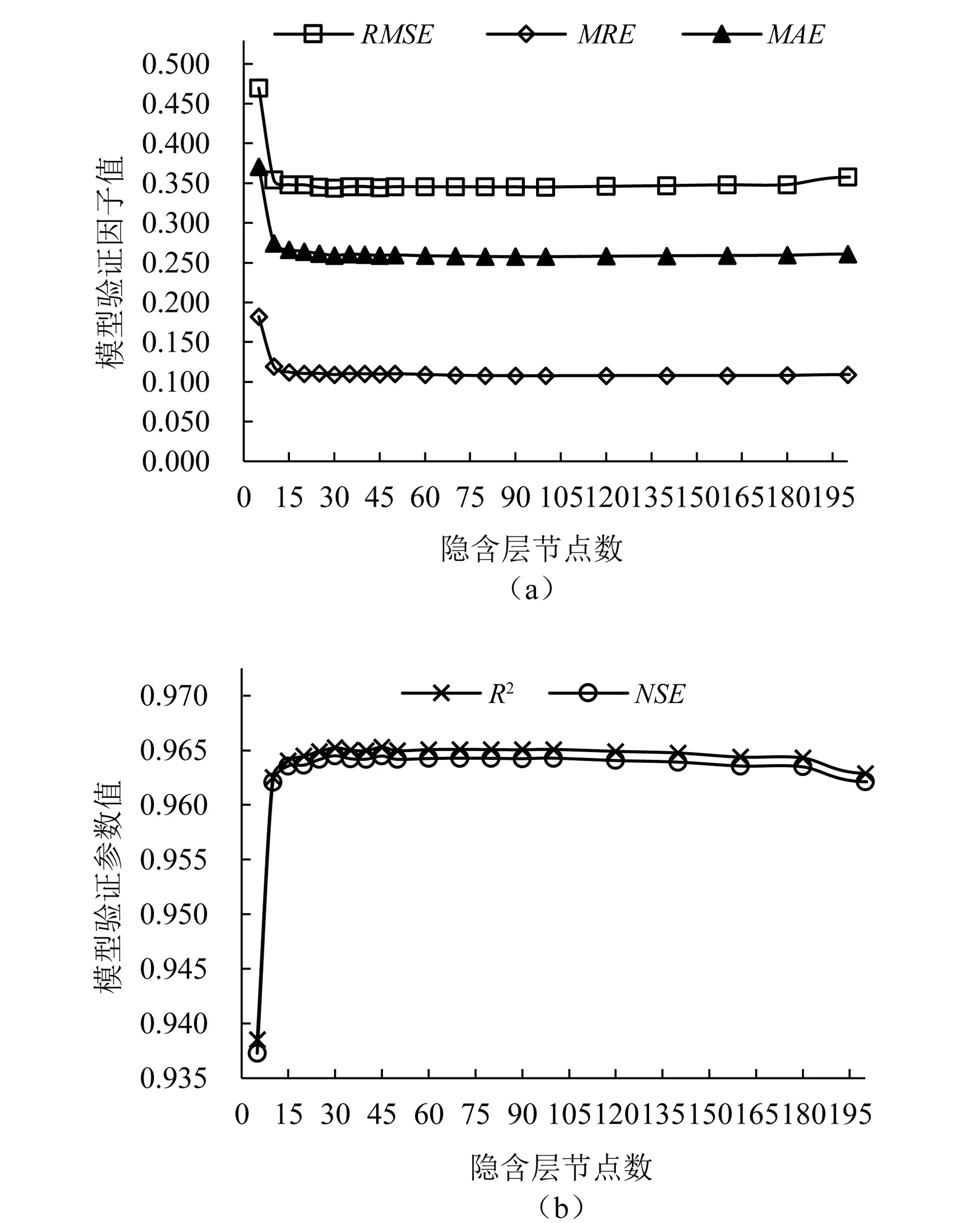
图3 各模型验证因子与隐含层节点数的关系Fig.3 Relationship between the verification factor of each model and the number of hidden layer nodes

由图3可知，随隐含层节点数的增加，RMSE呈先减小后趋于稳定再增大的趋势，MRE、MAE呈先减小后趋于稳定再增大的趋势，R2和NSE均呈先增大后趋于稳定的趋势。当隐含层节点数小于60时，模型模拟精度随隐含层节点数增加明显提高；当隐含层节点数达60～100时，RMSE、MAE、MRE、R2和NSE分别稳定趋于0.345 2 mm/d、0.257 5 mm/d、10.8%、0.965 1和0.964 3；当隐含层节点数达到120后，RMSE与R2呈减小趋势，模型精度开始降低。因此，隐含层节点数为60～100时ELM-sin7能取得较高的模拟精度。

增加隐含层节点数时，ELM模型能取得更高的精度，是由于增加隐含层节点数目可以实现将线性不可分的样本映射到高层的线性可分空间，获得更好的泛化能力。本研究仅选取了3种激活函数构建模型，基于输入较少气象因子仍能取得较高精度的ELM-sin7模型进行了隐含层节点数的讨论，发现随隐含层节点数增加，模型精度先有明显提高后趋于稳定，但当隐含层节点数过多时，出现精度下降的现象，说明隐含层节点数过多会导致过拟合问题，模型稳定性遭到破坏。

2.3 ELM-sin在相同输入因子下与物理模型精度比较

将基于温度资料的H-S模型与ELM-sin模型进行比较，基于温度和辐射资料的MK、I-A与ELM-rad模型进行比较，比较结果如表5所示。仅输入Tmax、Tmin时，ELM-sin8的R2、NSE、RMSE和MAE分别为0.797 1和0.765 1、0.922 1和0.694 0 mm/d，H-S模型的R2、NSE、RMSE和MAE分别为0.762 7、0.594 2、1.199 4和0.915 2 mm/d，可见，ELM-sin8的精度明显高于H-S模型。输入Tmax、Tmin、n三个气象因子时，ELM-rad5的R2、NSE、MAE、RMSE分别为0.822 5、0.785 8、0.664 1、0.882 3 mm/d，而I-A和MK的R2均小于0.77，NSE均小于0.63，RMSE均大于1.1 mm/d，MAE均大于0.9 mm/d，表明ELM-sin5的模拟精度明显高于MK模型和I-A模型。因此，仅输入温度时推荐用ELM-sin8代替传统物理模型进行西北地区ET0模拟；仅输入温度和日照时数时，推荐用ELM-rad5模型。

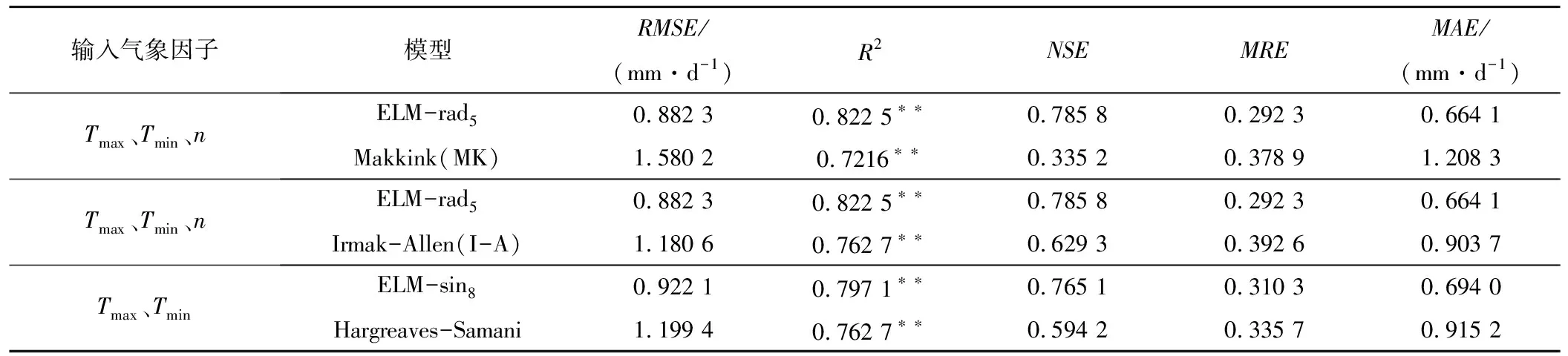
表5 ELM-sin模型、ELM-rad模型与其他物理模型模拟精度比较Tab.5 Comparison of simulation precision between ELM-sin model、ELM-rad model and other physical models

2.4 ELM-sin7模型可移植性分析

基于激活函数“sin”的ELM-sin7模型(仅输入Tmax、Tmin、u2)在较少参数输入下ET0模拟精度较高，为检验ELM-sin7在西北旱区的普遍适用性，分别选取模拟站点P和训练站点T，形成12组模拟集和训练集样本，构建ELM-sin7模型，模拟结果见表6。

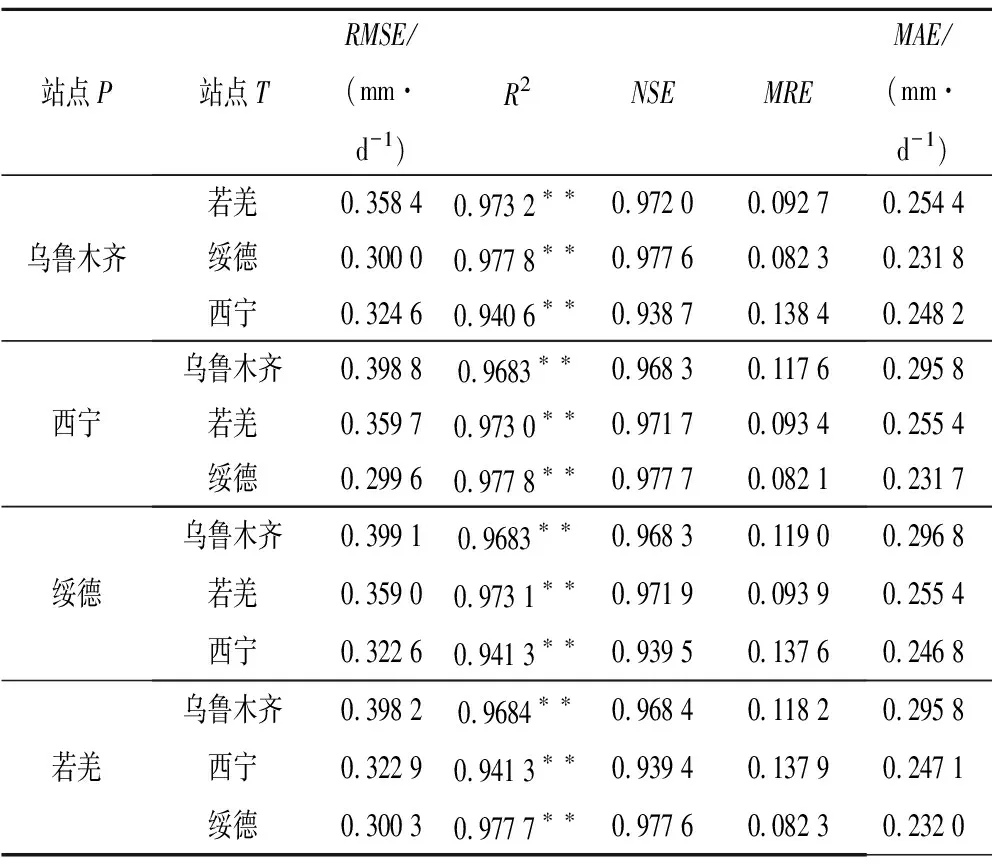
表6 不同站点间ELM-sin7模型可移植性结果Tab.6 ELM-sin7 portability results among different stations

由表6可知，各站点组合下的ELM-sin7的R2均大于0.94，NSE均大于0.93，RMSE、MRE和MAE分别小于0.40 mm/d、14%和0.30 mm/d，模型精度较高，与站点组合前运行结果相比精度下降甚微，其中除以西宁作为训练站点的3种站点组合外，其余的ELM-sin7的R2和NSE均大于0.96，MRE均小于12%，与原站点数据作为训练集和测试集的模拟精度相当，且以绥德作为训练站点的3种站点组合模拟精度较原有数据模拟精度明显提高。因此，ELM-sin7在各站点之间的可移植性较好，在西北旱区的适用性强。

3 结 论

(1)基于“sin”、“radbas”、“hardlim”三种激活函数构建ELM模型，发现相同气象因子输入下，基于“sin”和“radbas”的ELM-sin和ELM-rad模型精度总是高于基于“hardlim”的ELM-hard模型，因此在模拟西北旱区ET0时不建议采用“hardlim”激活函数构建ELM模型。而气象因子较少时，ELM-sin较ELM-rad能更精确地模拟ET0，其中以温度和风速为输入项的ELM-sin7模型的R2、NSE和RMSE分别为0.965 2、0.964 4和0.344 8 mm/d，因此，推荐基于温度和风速的ELM-sin7作为西北旱区较少气象因子输入下的ET0模拟模型；仅以温度作为输入项时，ELM-sin8的RMSE、R2和NSE分别为0.922 1 mm/d、0.797 1、0.765 1，模型精度较ELM-rad8更高，因此，仅输入温度条件时，推荐基于温度资料的ELM-sin8作为西北旱区的ET0模拟模型。

(2)对隐含层节点数进行研究表明，仅输入Tmax、Tmin和u2的ELM-sin7模型的隐含层节点数小于60时，其精度随隐含层节点数增加而提高；隐含层节点数为60～100时，ELM-sin7模型的RMSE、MAE、MRE、R2和NSE分别趋于0.345 2 mm/d、0.257 5 mm/d、10.8%、0.965 1和0.964 3；隐含层节点数大于120时，模型精度呈下降趋势。因此，在仅输入温度和风速的情况下，利用ELM-sin7模型对西北旱区ET0进行模拟时，建议设置模型隐含层节点数为60～100。

(3)通过将ELM模型与H-S、MK和I-A模型进行对比发现，仅输入温度时，ELM-sin8模型精度高于H-S模型；仅输入温度和日照时数时，ELM-rad5模型优于MK模型和I-A模型。因此仅基于温度或温度和辐射资料进行西北旱区ET0模拟时，推荐使用ELM-sin8和ELM-rad5模型。

(4)ELM-sin7模型可移植性分析表明，在各训练站点与模拟站点的组合下，ELM-sin7模拟精度较高，R2和NSE分别大于0.94和0.93，RMSE均小于0.40 mm/d。可见，在西北旱区内，ELM-sin7模型的可移植性和泛化能力较好，因此，某站点气象资料缺失时，可用区域内临近站点的气象资料进行该站点的ET0模拟。

本文仅选择了西北旱区的4个站点进行模型构建，在组合气象参数时，参考其他文献选取了精度最高的9种组合，未列出所有可能组合。在后续研究中应以区域实测蒸散量为模拟目标值，建立基于ELM的区域蒸散量模拟模型，以为西北旱区的高效节水灌溉和区域水资源管理提供更精确的科学依据。