在实验中促进小学数学概念建构
2019-01-19徐学萍
徐学萍

摘 要 著名教育学家苏霍姆林斯基曾经说过,儿童的智慧就在他们的指尖上。在小学数学教学中也是如此,通过实验,可以更好地帮助学生构建数学知识概念。以“轴对称图形的初步认识”教学为例,阐述相关的实验教学方法。
关键词 数学实验;小学数学;轴对称图形;多媒体
中图分类号:G623.5 文献标识码:B
文章编号:1671-489X(2019)17-0114-03
1 前言
皮亚杰认为,知识概念既不预成于内,也不预成于外,学生只有学会自主构建知识概念,知识才真正地属于学生。数学实验将“教”与“学”建立在“做”的基础之上,通过直观的实践操作,化解知识学习的抽象之感。在“轴对称图形的初步认识”这节课的教学中,运用数学实验的方式,可以更好地帮助学生构建知识概念。
2 “轴对称图形的初步认识”教学介绍
“轴对称图形的初步认识”是小学数学三年级上册的重要知识,本节课教学要实现三个方面的教学目标[1]:
1)帮助学生感知生活中的轴对称现象,有效地识别轴对称图形的基本特征,可以根据轴对称图形的特征,有效地识别轴对称图形,并且可以自主尝试去创造轴对称图形;
2)从学生的生活经历出发,从生活现象中抽象出轴对称图形,同时不断地积累相关的思维活动经验,并逐渐发展形成对空间的初步概念;
3)使学生体会轴对称图形在现实生活中的应用,发现数学之美,促使学生的数学学习兴趣得到提升。
在“轴对称图形的初步认识”这节课的教学中,最大的难点是认识轴对称图形的基本特征,可以有效地识别平面图形中一些简单的轴对称图形图案。在“轴对称图形的初步认识”这节课教学中,实验教学方式是极为契合实用的,符合学生的认知水平和心理特点,可为学生的数学知识概念建构提供保障。
3 在实验中促进小学数学概念建构:以“轴对称图形的初步认识”为例
演示实验,发现现象 演示实验是一种常见的数学实验教学方式,可通过直观的形象帮助学生化解数学知识学习困难,加深学生对数学知识的感受印象。在“轴对称图形的初步认识”教学中,教师可在课程开始之初,通过演示实验调动学生的学习兴趣,促使学生发现数学知识现象。如在演示实验中,教师可以通过多媒体教学工具,为学生播放“小朋友玩飞机模型”的视频:一位小朋友的飞机模型原本飞得比较平稳,并且飞得很高、很远,但由于在飞机落地的时刻,飞机模型一侧的机翼折断了,然后就再也无法起飞了。在这样的演示视频播放后,教师可以向学生提出问题:“为什么小朋友的飞机模型机翼折断后,就再也无法起飞了?”在学生思考问题的过程中,教师可以为学生出示“机翼折断前后的飞机图”,引导学生对比分析两幅图示之间的差别。此时学生就会发现,当飞机机翼一模一样时,飞机才能飞得平稳;而当飞机机翼折断时,飞机就不再平衡了。
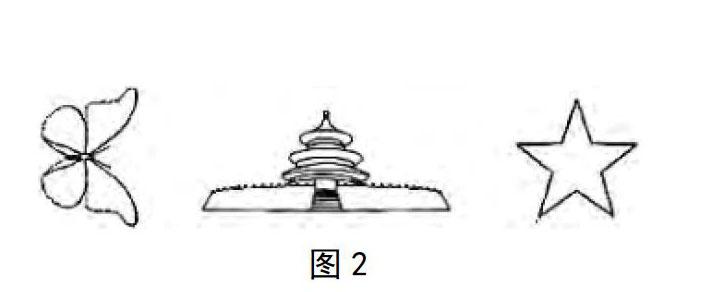
教师可以带领学生仔细观察完好的飞机图片,引导学生发现在飞机模型中有一条直线,沿着这一条直线,可以将飞机直接分割成两个一模一样的部分;然后让学生找出这条直线到底在什么位置,直线的两边有怎样的特点。通过这样的演示实验,引出“轴对称图形”的概念。教师还可以为学生展示图1所示图形,帮助学生认识到和飞机一样具有轴对称特性的图形还有很多,如蝴蝶、天坛、五角星都是轴对称图形;但是最后的衣服图形下摆一边长一边短,所以是不對称的。借助这些演示实验,帮助学生发现、理解轴对称图形概念。
尝试实验,感知特征 在小学数学教学中,尝试实验为学生提供了自主操作尝试的机会,有助于学生主体构建知识,并促使学生的思维能力得到有效培养。在“轴对称图形的初步认识”教学中,若是把这些对称图形画出来,就可以得出图2所示图形。在尝试实验之中,教师可以引导学生大胆尝试,想一想如果把这些轴对称图形剪下来,有哪些方法?最简单的方法是什么?
如有的学生就提出沿着图形的边线,慢慢地将图形剪下来;还有的学生提出,将这些图形对折,这样沿着图形一半的边形剪下来,也可以得到完整的图形。教师可以让学生结合自身的猜想,亲自动手进行尝试,但实际动手前可以让学生先进行合作思考,如:“采用先对折再剪出一半图形的方式,对折的线是任意选取的吗?”学生通过探讨尝试就会发现,先对折,再沿一半图形的边线剪,是可以得到相应图形的,但是对折的线不是任意选取的。如在蝴蝶图形中,只有沿着两触角之间横向对折,确保蝴蝶图的上下两边完全相同,翅膀与翅膀、身体与身体的边线都重合,然后进行裁剪,才能够得出想要的蝴蝶图形,不然是无法剪出的。而当学生尝试用对折线剪出完全重合的图形时,学生自然而然地就会明白什么是轴对称图形,并会明白能够让对折两边完全重合的线,就是轴对称图形的对称轴。在尝试实验之中,学生可以更好地感知轴对称图形的特征。
验证实验,掌握方法 验证实验也是一种常见的数学实验方式,通过验证实验,可以帮助学生解答心中的疑惑,促使学生对数学知识有更加深刻的认识感知。在“轴对称图形的初步认识”教学中,验证实验的使用主要是为了判断“某一图形是否为轴对称图形”[2]。
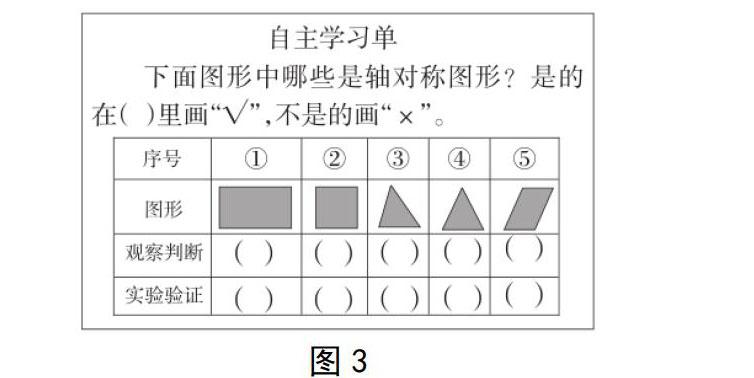
首先,判断平面图形是否为轴对称图形。如教师为学生出示图3,让学生判断这些平面图形之中哪些为轴对称图形。在这个过程中,教师可以让学生思考:轴对称图形最主要的特征是什么?如有的学生会回答:“图形对折后,两边可以完全重合。”这就是重要的验证依据,学生可以通过观察和动手两种方式做出实验验证,最后会发现①②④为轴对称图形,③⑤不是轴对称图形,它们不管如何对折,都无法得出完全重合的图案。
其次,判断生活图案。教师可以为学生出示中国工商银行标志、车轮图案、水杯图案等,判断这些生活图案是否为轴对称图形。让学生先观察,再去进行实验验证,并重点探讨这些轴对称图形的对称轴位置在哪儿,在验证实验过程中进一步巩固轴对称图形的判断方法,提升空间想象力。
想象实验,深化认识 数学实验本就是“做”与“思”有效融合的过程,若是可以让学生在“做”的过程中不断向“思”的高度提升,对学生数学学习发展无疑是有诸多裨益的,而想象实验为学生深化认识思考提供了机会。在“轴对称图形的初步认识”教学中,想象实验的组织主要包括两个方面。
1)在变化中体验的想象实验。在教学过程中,教师可以为学生出示图4所示交通标志,先让学生判断第一个交通标志是否为轴对称图形,然后将这个交通标志依次旋转,得到右边的三幅图示,并让学生判断后面的三个图示是否为轴对称图形,以此让学生说说自己的发现。这就是一种想象实验的方式。通过实验,学生会发现,轴对称图形无论做出怎样的旋转,都不会改变其为轴对称图形的本质事实。
2)从不同角度观察对称物体的想象实验。教师可以为学生出示一个生活模型图片,以飞机模型图示为例,引导学生想象从前、后、左、右四个方向观察这一飞机模型图片,并想象判断自己看见的图形是否是轴对称图形。而在这样的想象实验中,学生又会有新的发现,那就是立体模型中轴对称的物体从不同的角度观察并画到平面上,可能得到轴对称图形,也可能得到非轴对称图形。
在这样的想象实验教学中,学生对轴对称图形的认识不会停留在简单的判断上,会发现轴对称图形的对称性不会随它的位置改变而发生改变,但是通过不同角度去观察同一轴对称物体,看到的形状是可能发生改变的。在想象实验中帮助学生理清对称现象与轴对称图形之间的辩证关系,深化学生对轴对称图形知识的认识。
操作实验,构建知识 在“轴对称图形的初步认识”教学中涉及的操作实验有很多,包括拼摆实验、折纸实验等,通过这些动手操作实验,可以帮助学生更加全面地构建数学知识。
1)拼摆实验,凸显本质属性。小学数学知识具有一定的抽象性,而学生又缺乏理性认识,因此学起来往往非常困难。在“轴对称图形的初步认识”教学中,教师可以通过设计拼摆实验的方式,帮助学生构建知识认识。如为学生提供图5所示图片,让学生通过亲手拼摆的方式,猜一猜上面一排的扑克图形是从下面一排的扑克纸牌之中的哪一张剪下来的。这样的拼摆实验操作方式可以帮助学生加深对轴对称图形的空间认识,从而清晰理解轴对称图形的本质属性,为学生的主体知识构建增添动力。
2)折纸实验,积累活动经验。动手操作是数学实验的基本方式,动手操作实验可以充分地调动学生的多种感官,促使学生手脑并用,从而更进一步加深学生对数学知识的认识,促使学生的动手实验能力得到增强。在“轴对称图形的初步认识”教学中,折纸实验是一种非常适用的教学方式,如可以向学生提出这样一个问题:“把一张纸对折两次,剪出来会是什么样子?”通过这样的折纸实验,让学生自己尝试设计轴对称图形,同时引导学生:“如果对折更多的次数,结果会怎样呢?”这样的实验教学方式极具开放性。教师也可以将学生设计的作品展示出来,在激发学生学习兴趣的同时,更好地帮助学生积累构建知识。
4 结语
“轴对称图形的初步认识”是小学阶段重要的几何知识内容,而数学实验教学方式充分考虑到学生的心理特点和认知水平,可让学生在动手操作过程中理解轴对称图形的概念,促使学生的空间概念得到发展,从而加快学生主体知识构建。总之,开展小数数学实验教学是一种可行的方式。
参考文献
[1]孙冬梅.借助数学实验 促进概念教学:“轴对称图形的初步认识”教学实践与思考[J].小学数学教育,2017(24):
50-51.
[2]戴文亞.在数学实验中促进概念建构:以“轴对称图形的初步认识”为例[J].小学数学教育,2016(22):38-39.
