基于加权Schatten-p范数与树结构稀疏分解的目标显著性检测
2019-01-19钱文超曹飞龙
钱文超,曹飞龙
(中国计量大学 理学院,浙江 杭州 310018)
在计算机视觉领域里,目标显著性检测已经成为一个具有挑战性的热门话题,其主要目的是提取图像的重要信息,即人们感兴趣的区域.近年来,目标显著性检测已被有效地运用于计算机视觉任务中,如图像检索[1-2]、图像分割[3-4]以及对象识别[5-6].
显著性检测的方法一般分为两大类.一类是基于数据驱动的自下而上的方法[7-9],其主要依赖于显著对象或背景的一些先验知识,例如颜色、纹理和位置等;另一类是基于目标任务驱动的自上而下的方法[10-11],该类方法需要利用标签进行有监督的学习训练.随着低秩矩阵恢复研究的兴起,很多学者也将其原理应用到目标显著性检测问题上,结合自下而上的方法,给出了一些基于低秩矩阵恢复的显著性检测方法[12-15].
假设一张图像可以分成信息冗余部分(即图像背景,通常处于低维特征子空间,具有低秩或近似低秩结构)和显著目标部分(即显著对象,具有稀疏结构,可视为稀疏噪声或误差).换言之,对于给定的图像特征矩阵F∈Rm×n,可以拆分成一个对应图像背景的低秩矩阵L∈Rm×n和一个对应显著对象的稀疏矩阵S∈Rm×n.基于这样的假设,目标显著性检测可以看成是矩阵的低秩稀疏分解问题:
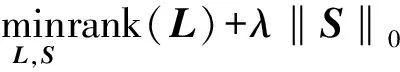
(1)
其中,rank(·)为秩函数,λ为正则化参数,‖·‖0为l0范数.
由于秩函数是非凸的,并且不连续,因此(1)是一个NP难问题.所以,根据压缩感知[16-17]的理论,利用核范数(Nuclear Norm,简写为NN)和l1范数分别对秩函数和l0范数进行替代,将非凸优化问题(1)转化成以下凸优化问题:

(2)

尽管一些基于核范数的最小优化模型能较好地逼近非凸优化模型(1),且具有很强的理论保证,但在实际应用中却只能获得次优解.这是因为所有非零奇异值对秩函数的影响是相同的,而核范数将所有非零奇异值加在一起,并且同时最小化,使得奇异值具有不同的贡献.因此,核范数不能成为秩函数的最佳近似替代.

受加权Schatten-p范数的启发,为了提高显著性检测的精确度,我们利用加权Schatten-p范数的思想,对背景矩阵L进行低秩约束,并引入具有树结构稀疏特性的l2,1范数和图像拉普拉斯正则化对目标矩阵S进行稀疏约束,建立一个用于目标显著性检测的基于加权Schatten-p范数的低秩树结构稀疏分解模型(简称为WSPN-LRSSD).然后,运用交替方向迭代算法(alternating direction method of multiples,ADMM)求解模型.最后,通过目标显著性检测实验说明该模型的优势.
本文内容安排如下.在第一部分中,详细介绍所提出模型的结构以及模型求解过程.第二部分通过对实验结果的分析,说明本文模型的优势.最后在第三部分中得出结论.
1 WSPN-LRSSD模型建立与求解
1.1 WSPN-LRSSD模型
给定一张输入图像I,首先通过简单线性迭代聚类方法[23](simple linear iterative clustering,简写为SLIC)将I分割成互不重叠的N个超像素块.然后,对于每个超像素块Pi提取一个D维的特征向量,记为fi∈RD.最后,将所有超像素块的特征向量整合成一个表示图像I的特征矩阵F=[f1,…,fN]∈RD×N.
本文提出如下基于加权Schatten-p范数的低秩树结构稀疏分解模型(WSPN-LRSSD):
s.t.F=L+S.
(3)
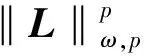
1.1.1 低秩正则化
图像背景通常处于低维空间中,具有低秩或近似低秩的结构,因此,对图像背景可以进行低秩约束:
(4)
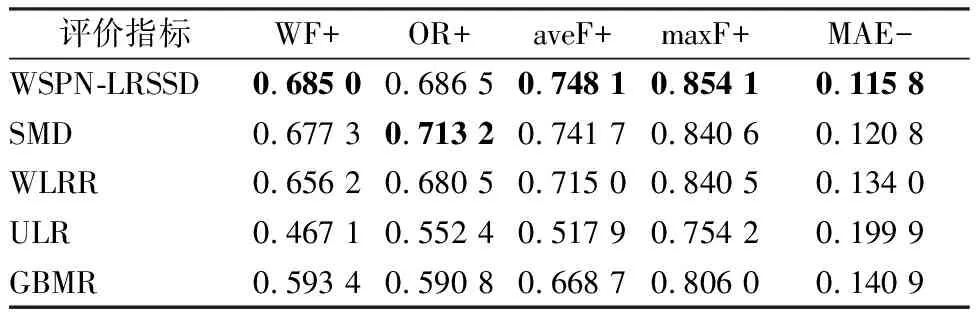
其中,σi(L)为L的第i个奇异值,并且奇异值按从大到小顺序排列,ωi为对应σi(L)分配的权重,0 (5) 其中,C=2max(m2,n2),ε=10-16. 1.1.2 稀疏正则化 模型(2)中对稀疏矩阵S进行了l1范数正则化,只是单独处理了矩阵S的列,并没有考虑S的空间结构.对于显著性检测来说,显著对象的内在结构是非常重要的.所以,本文引入基于树结构稀疏的l2,1范数对目标矩阵S进行稀疏约束,使模型更加鲁棒. 首先,介绍一种结构层次划分的方法,即索引树. 然后,我们利用索引树表示图像块之间的空间关系.基于加权树结构稀疏的l2,1范数可以表示为 (6) 在目标显著性检测中,把显著对象视为稀疏噪声,然后从图像背景中提取出来.但在实际图像上,一些显著对象与背景是很相似的,导致提取的显著对象不清晰.为了解决这个问题,先对图像进行背景先验的提取,然后判断每个像素(超像素)是否属于前景显著对象.我们利用每个超像素的图像位置、颜色和边缘先验信息,融合成图像背景先验. 首先,利用超像素到图像中心距离的高斯分布来生成位置先验: (7) 其中,σ2为高斯分布方差,c为图像中心. 其次,根据人眼对暖色系(如红色和黄色)的敏感性,利用文献[25]的方法,对每个超像素颜色先验Co(i)进行提取. 然后,受文献[11]和[26]的启发,通过计算图像超像素Pi与边缘超像素的交集长度,以衡量Pi与图像边缘的连通程度,从而获得图像边缘先验信息: (8) 其中,B表示边缘超像素集合,qi表示超像素Pi内的像素个数,|·|表示交集长度,即两个超像素连接的像素个数. 最后,将上述三个先验相乘,并进行归一化处理,得到值在区间[0,1]内的背景先验权重: Ω(i)=Lo(i)·Co(i)·Bo(i). (9) 再融合并扩充为一个背景先验权重矩阵: (10) (11) 1.1.3 图像拉普拉斯正则化 为了保留原始图像的固有局部结构,在目标函数中考虑加入图像拉普拉斯正则化约束.文献[27]提出这样的假设:如果两个数据点xi和xj在数据分布中的固有几何位置接近,那么在新的基中这两个点的表示也彼此接近.由此可推出,如果两个相邻图像块的特征相似,则它们在子空间中的表示应该也彼此接近;反之亦然.从而,我们对显著对象定义拉普拉斯正则化为 (12) 其中,si表示S的第i列元素,Θ∈RN×N为图像关联矩阵,其表达式为 (13) 本小节介绍用ADMM方法求解模型(3),先将(3)式转化为 (14) 然后构造模型(14)的增广拉格朗日函数 (15) 其中,Y1和Y2是拉格朗日乘子,μ>0是惩罚参数. 固定S和J,更新L: (16) 引理1[22]已知矩阵QL的奇异值分解为QL=U∑VΤ,∑=diag(σ1,…,σr),则(16)式的最优解为L*=UΔVΤ,其中Δ=diag(γ1,…,γr)是如下优化问题的解: (17) 利用广义软阈值算法(Generalized Soft-Thresholding,简写为GST)[28]求解(17)中的子问题,其阈值算子为 (18) 固定L和S,更新J: (19) 对式(19)关于J求导并令其等于零,得到 Jk+1=(μkSk+Y2,k)(2βMF+μkI)-1. (20) 固定L和J,更新S: (21) (22) 最后,更新拉格朗日乘子和惩罚参数,得到 Y1,k+1=Y1,k+μk(F-Lk+1-Sk+1), (23) Y2,k+1=Y2,k+μk(Sk+1-Jk+1), (24) μk+1=min(ρμk,μmax). (25) 其中ρ>1是一个常数. 将上述模型的求解过程整理为如下算法1. 算法1(ADMM求解WSPN-LRSSD模型): 输出:L和S; 初始化:L0=0,S0=0,J0=0,Y1,0=0,Y2,0=0,μ0=0.1,μmax=1010,ρ=1.1,以及k=0; 1:While not converged do 2:固定其它量,由式(16)更新Lk+1; 3:固定其它量,由式(19)更新Jk+1; 4:固定其它量,由式(21)更新Sk+1; 5:由式(23)与(24)分别更新Y1,k+1和Y2,k+1; 6:由式(25)更新惩罚参数μk+1; 7:k=k+1; 8:End while 9:返回Lk+1和Sk+1. 通过比较WSPN-LRSSD和其他四种方法:SMD[13]、WLRR[12]、ULR[25]和GBMR[30],并在目标显著性检测上的实验结果,来说明我们所提出模型的优势.实验选取了三个数据库,包括ECSSD[31]、iCoSeg[32]以及Pascal1500[9]. 其中ECSSD包含了1 000张不同对象且场景比较复杂的图像,iCoSeg包含了38个不同对象的若干张图像,而Pascal1500则是包含了1 500张自然图像,显著对象出现在各种位置,并且背景区域更加混乱.本文所有实验的环境是Intel(R)Core(TM)i3-4150 CPU @ 3.50 GHz处理器,在内存为4 GB的计算机,MATLAB版本为R2014a上运行. 为了说明实验效果,我们引入三个模型评价指标. 1)平均绝对误差(mean absolute error,简写为MAE)[33],即检测出的显著对象与真实二值化显著对象的平均绝对误差,定义为MAE=mean(|S-GT|); 在本文实验中用到的分别是加权F-measure指数(WF)、平均F-measure指数(aveF)和最大F-measure指数(maxF).这五个指标中,除了MAE值越小越好外,其余都是值越大越说明效果好. 为了说明不同p值对模型的影响,选取p为[0.2,0.8]中间隔为0.1的七个值,分别在ECSSD上进行实验.参数α和β分别设置为0.35和1.1. 针对于p值的不同选取,从图1的四条曲线可知,当p=0.3时显著性检测效果最好.在另外两个数据库上也得到相同的结论. 通过WSPN-LRSSD与SMD、WLRR、ULR以及GBMR四种方法分别在ECSSD、iCoSeg和Pascal1500三个数据库上进行实验对比,来说明所提出方法的优势.依据上述结论,在所有实验中设置p=0.3. 图1 不同p值对ECSSD数据库的显著性检测结果Figure 1 Results of salient object detection under different p on ECSSD database 表1、表2和表3是在三个不同数据库中,五种方法分别进行目标显著性检测的评价指标结果.从整体结果上看,我们的方法相比其他的方法具有较好的检测能力,即使在比较复杂的一些图像上,都能很好的检测出显著目标. 表1 五种算法在ECSSD数据库中的显著性检测结果Table 1 Results of salient object detection on ECSSD database by five algorithms 注:“+”表示值越大越好;“-”表示值越小越好;黑体数值为最优值 为了进一步说明模型的优势,在图2中展示了部分由各种方法进行目标显著性检测的视觉效果图.从左往右依次为原图像、真实显著对象(GT)、WSPN-LRSSD、SMD、WLRR、GBMR以及ULR方法得到的显著目标.从图上可以看出,WSPN-LRSSD方法检测出的显著目标要比其他方法的更接近真实显著目标.另外,WSPN-LRSSD算法对不同数据库中的图像的平均运行时间为2.74 s,在时间成本上消耗较小,但是比SMD方法的时间还是长了一倍多. 综上所有分析,本文提出的模型在目标显著性检测问题上具有良好的表现,优于其他四种检测方法. 表2 五种算法在iCoSeg数据库中的显著性检测结果Table 2 Results of salient object detection on iCoSeg database by five algorithms 表3 五种算法在Pascal1500数据库中的显著性检测结果Table 3 Results of salient object detection on Pascal1500 database by five algorithms 图2 五种方法在不同数据库的显著性检测视觉效果图Figure 2 Visual comparisons of saliency maps of five methods on different databases 本文将目标显著性检测视为矩阵低秩稀疏分解问题,并提出了基于加权Schatten-p范数与树结构稀疏分解模型(WSPN-LRSSD).利用加权Schatten-p范数对图像背景进行低秩约束,而对于显著目标,则采用具有树结构稀疏特性的l2,1范数和图像拉普拉斯正则化进行稀疏约束.同时,为了更好地检测出显著目标,还对图像进行了背景先验提取,增大了图像背景与显著目标的差异性.实验结果证明,不管是评价指标还是视觉效果,本文模型具有更好的显著性检测性能. 在未来的工作中,考虑要缩短实验时间以减少时间成本.同时,改进背景先验的提取方法,使得获取的背景先验更加有利于显著目标的检测.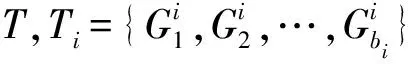
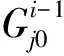

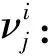
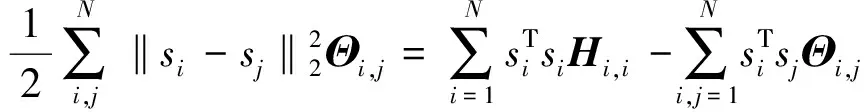
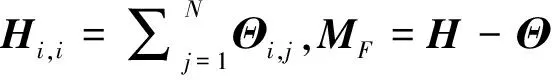
1.2 WSPN-LRSSD模型求解

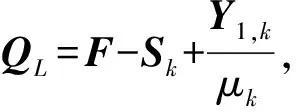
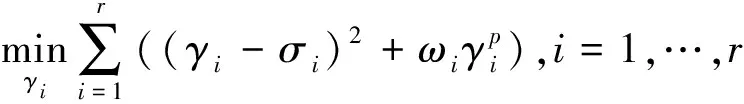
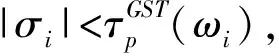



2 实验结果与分析
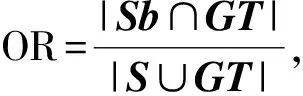
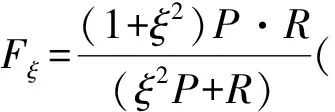
2.1 不同p取值的影响
2.2 仿真结果及分析




3 结论与展望
