基于NSGA-II的行星减速器多目标优化设计

（河南理工大学，焦作 454000）

0 引言

提升绞车用于中小型煤矿，金属矿竖井和斜井，提升煤、矿石、矸石、运输材料及设备。行星减速器具有体积小、传动范围大、承载能力高等优点，是提升绞车中广泛采用的减速装置。行星减速器的多目标优化难点在于离散变量多，变量间存在相互约束条件，以及目标函数的权重系数选取困难，导致齿轮参数的选取更多依赖设计人员的工程经验，得到的方案仅为可行方案而非最优方案。

为解决上述问题，西庆坤等[1]运用MATLAB软件编制遗传算法优化程序，解决了摆线针轮行星减速器的传动效率低，结构不够紧凑的问题。杜兴等[2]采用粒子群算法的离散变量处理策略对行星减速器进行求解，克服了权重系数选取的主观性和不确定性。Shi Jie Wang等[3]为实现减速器在高温、高压的大跨度井下条件下连续工作，基于可靠性理论和优化设计方法，建立NWG型齿轮减速器的可靠性优化数学模型。解决了齿轮减速器的可靠性设计和疲劳寿命等问题。张欢[4]针对某电动轮矿用自卸车轮边三级行星减速器在电制动工况时,第三级太阳轮、行星轮接触安全系数偏低、第三级太阳轮使用寿命偏低的问题，基于Romax搭建分析模型，对第三级太阳轮、行星轮修形进行优化分析，为行星减速器优化设计提高产品强度和使用寿命提供一定的参考依据。

然而行星减速器的设计必须兼顾体积及齿轮强度两个重要指标，这样才能使行星减速器的工作能力达到最优。为此，本文以实现降低体积、提高齿轮强度为设计目标，利用遗传算法对行星减速器进行多目标优化设计。

1 体积计算

行星减速器结构如图1所示，电机通过弹性柱销联轴器带动中心太阳轮转动。制动离合器盘，与离合器盘固结连接的内齿圈固定不动，动力由行星架输出。该行星轮系属于2K-H型，其结构简图如图2所示。

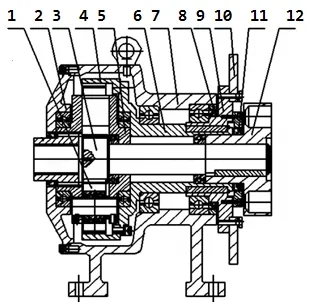
图1 行星减速器装配图

由于2K-H型行星机构中内齿圈的外形尺寸取决于由中心齿轮轴及行星轮的尺寸，因此行星机构体积可取中心轮1和行星轮2的体积和，计算式为由于2K-H型行星机构中内齿圈的外形尺寸取决于由中心齿轮轴及行星轮的尺寸，因此行星机构体积可取中心轮1和行星轮2的体积和，计算式为：

图2 行星减速器机构简图

行星轮2的参数并不独立，依赖于中心太阳轮1的基本参数，按照行星轮系的传动比公式、太阳轮与行星架同心条件及行星轮均布安装条件[5]，体积算式可写为：

其中：Z1为中心太阳轮的齿数，m1为中心太阳轮模数，b1为中心太阳轮齿宽。初始条件为：传动比u＝5.8，传动比相对误差＜0.02，行星轮个数k=3。

2 强度分析

齿轮的参数不仅影响轮系的体积及传动效率，还影响了齿轮的承载能力。行星轮系中若各齿轮材料均相同，且均为硬齿面齿轮，则中心太阳轮的强度低于太阳轮和行星轮。目前计算一般使用的齿轮传动时，通常按保证齿轮弯曲疲劳强度和齿面接触疲劳强度两准则进行计算。本文按提高弯曲疲劳强度为目标进行设计，将接触疲劳强度作为约束条件。对于闭式直齿轮，弯曲疲劳强度条件为[6]：

式中：[σ]F为齿轮的弯曲疲劳许用应力；KF为弯曲疲劳强度计算载荷系数；YFa为齿形系数；YSa为应力修正系数；Yε为弯曲疲劳强度重合度系数。为提高弯曲疲劳强度，建立第二个目标函数：

3 多目标优化模型

3.1 目标函数

利用行星轮系效率分析结果及体积计算式，多目标优化目标函数Q表示为：

3.2 设计变量X

影响目标函数的参数包括中心太阳轮的齿数、模数和齿宽，则设计变量X为：

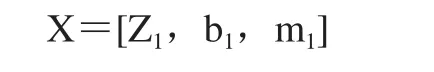
3.3 约束条件

在满足体积最小以及提高弯曲疲劳强度的前提下，还需考虑齿轮接触疲劳强度，行星轮系配齿等因素，为此建立包含接触疲劳强度、行星轮装配等约束条件。为保证相邻两行星轮不致相互碰撞，各轮齿轮应满足：

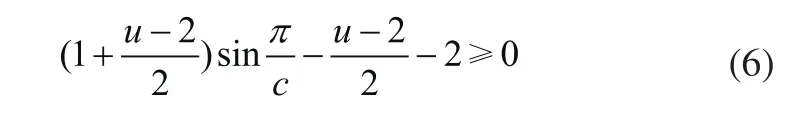
行星轮系中各齿轮材料均用38SiMnMo钢，表面淬火硬度HRC＝45～55。当齿轮材料及传动比已选定的情况下，影响齿面接触疲劳强度的主要因素是小齿轮直径，因此取中心太阳轮的接触疲劳条件作为约束：

式中：KH为载荷系数；φd为齿宽系数；[σ]H为齿轮的接触疲劳许用应力；ZE为弹性影响系数；ZH为区域系数；Zε为接触疲劳强度重合度系数；u0为中心太阳轮与行星轮齿数比。

3.4 优化模型

优化模型中各变量的取值范围直接影响优化结果，根据经验类比方法，确定齿轮1的参数取值区间如表1所示。

教学改革研究项目管理系统的实现 系统采用Java语言，以J2EE技术为基础，采用目前应用较为广泛的SSH Web框架，运用Struts+Spring+Hibernate技术搭建表示层、业务逻辑层、数据持久层和域模块层，建立结构清晰、可复用性好、维护方便的Web应用程序。

表1 设计变量的区间

通过目标函数及约束条件，建立变量为3维，具有4个不等式约束的非线性优化设计模型：

4 优化方法及分析

采用NSGA-II算法对行星减速器进行优化。该算法通过快速非支配排序算法对父代种群与子代种群合并，进行快速非支配排序，对种群分级。通过引入拥挤度和拥挤度比较算子选取合适的个体组成新的父代种群；由于引入精英策略来增大采样空间，克服了传统NSGA的计算复杂和共享参数难以确定的缺点，提高了算法的收敛性、鲁棒性和计算效率[7～9]。

NSGA-II优化算法的控制参数如下：种群规模为200，交叉概率为0.8，变异概率为0.1，最大进化代数为100。完成100代进化后，得到多目标优化Pareto最优解集，两目标值分布如图3所示。

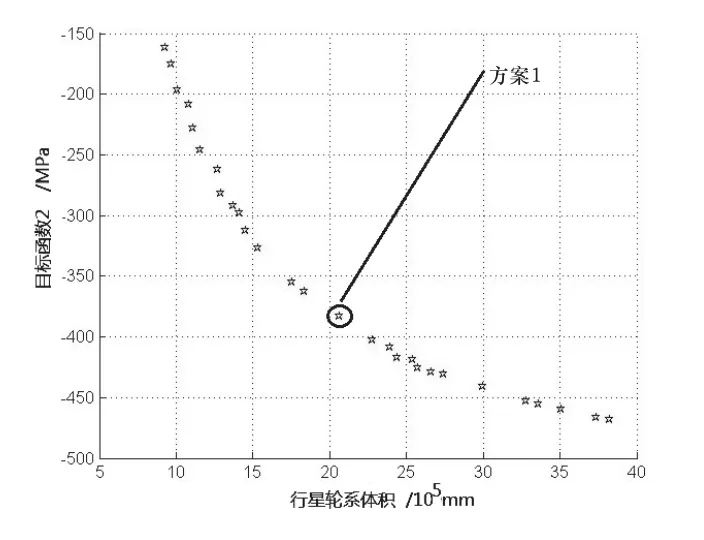
图3 最优解集分布图

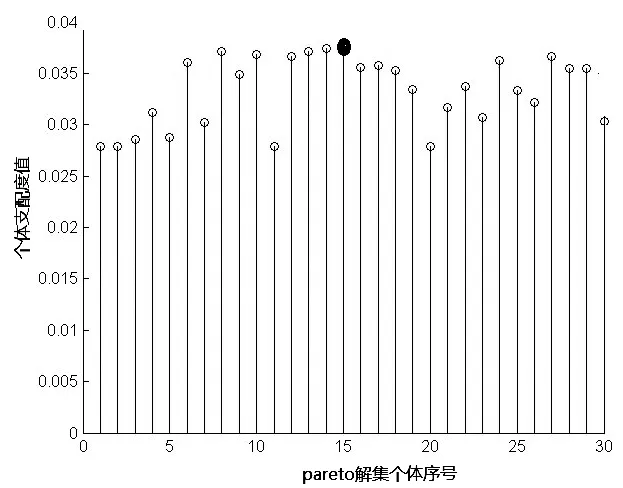
图4 Pareto解集的个体支配函数值

从图3可以看出，当行星轮系体积减小，弯曲应力亦随之增大，可知实现行星轮系体积最小与提高弯曲疲劳强度是一对矛盾的目标，不可能同时满足两个指标最优。

影响体积的三个参数分别是齿数，传动比，齿宽及模数，这些参数同时也影响弯曲强度，因此行星齿轮减速器体积与弯曲强度存在非独立的关系，从最优解集分布图中发现二者具有负相关性。

从支配值分布图中发现，Pareto解集中的第15号个体的支配值最大，15号个体在Pareto解集域中对应的方案1变量X为：

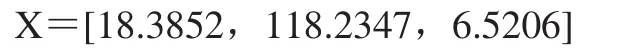
将遗传算法得到的各变量取整，齿数为18，齿宽为118mm，模数为6mm。按照行星轮系配齿条件，计算出行星轮齿轮及内齿圈齿数分别是33和84，优化后的行星轮系体积是1.44×106mm，齿轮的弯曲应力和接触应分别是237.32MPa和1047.6MPa，均小于材料的许用应力，满足齿轮的强度条件。

5 结论

1）本文以矿用提升车的行星减速器为优化对象，构建了基于多目标的优化数学模型，得到了经过100代迭代后的Pareto最优解集及目标分布图。

2）通过对比两目标的最优解分布图，发现行星减速器体积与弯曲强度之间呈现近似负相关的影响关系。

3）采用模糊集合理论对Pareto解域进行支配值计算，实现从Pareto最优解中选优，将方案1作为最终优化设计方案。克服了依据经验选择Pareto最优解的不确定性和主观性。

本文提出的优化设计方法满足了行星齿轮减速器多目标优化设计要求，同时也适用于其他类型的减速机的多目标优化设计。